Как найти время с помощью скорости и расстояния?
Чтобы узнать расстояние, нужно скорость умножить на время. Чтобы найти время, нужно расстояние разделить на скорость.
Как найти расстояние за минуту?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи: Заяц убегал от Волка со скоростью 1 километр за 1 минуту.
Как найти км в час?
Чтобы найти скорость, нужно расстояние разделить на время движения. Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
Как в математике обозначается скорость время и расстояние?
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой. Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут.
Как найти расстояние между двумя точками?
Вычисление расстояния между взятыми на плоскости двумя точками А(х А; у А) и В(х В; у В), выполняется по формуле d = √((х А – х В) 2 + (у А – у В) 2) , где d – длина отрезка, который соединяет эти точки на плоскости.
Сколько в среднем человек ходит км в час?
Средняя – 90 – 120 шагов в минуту, что составляет 4 – 5,5 км/ч; Быстрая – 120 – 140 шагов в минуту, что составляет 5,6 – 6,5 км/ч; Очень быстрая – более 140 шагов минуту, что составляет более 6,5 км/ч. Если человек старше 35 лет и никогда ранее не занимался спортом, то ему следует начинать с очень медленной ходьбы.
Сколько метр в одном км?
В 1 метре (м) содержится 100 сантиметров (см), 1 м = 100 см. В 1 километре(км) содержится 1000 метров, 1 км = 1000 м.
Что означает формула S V * t?
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t. Задачка 1.
Как записывается расстояние в математике?
Расстояние – это длина от одного пункта до другого. Большие расстояния, в основном, измеряются в метрах и километрах. Расстояние обозначается латинской буквой S.
Как найти расстояние между точками 7 класс?
Как найти расстояние между двумя заданными точками? Для того чтобы найти длину отрезка на координатной прямой надо из координаты ее конца вычесть координату начала по модулю.
Как узнать сколько километров?
Примечание.
- Откройте Google Карты на компьютере.
- Нажмите правой кнопкой мыши на пункт отправления.
- Нажмите Измерить расстояние.
- Чтобы создать путь для измерения, коснитесь любого места на карте. Точно так же можно добавить ещё несколько точек. …
- Когда закончите, на карточке внизу страницы нажмите «Закрыть» .
Сколько километров в 10000 шагов?
8 километров
В 10 000 шагов помещается от 7 до 8 километров в зависимости от длины шага. Они, конечно, не гарантируют полного здоровья, но могут повысить выносливость организма и его устойчивость перед инфекциями.
Какая скорость у человека в час?
30 км/ч — средняя скорость бега тренированного человека на короткой дистанции (100м — 400м). 20 км/ч — средняя скорость бега тренированного человека на средней дистанции (800м — 3км). 16 км/ч — средняя скорость бега тренированного человека на длинной дистанции (10км — 42км).
Как выглядит 1 километр?
Киломе́тр (сокращённо км, km) — широко распространённая кратная метру единица измерения расстояния. 1 км = 1000 м = 0,621 миль = 0,9374 версты = 1094 ярдов = 3281 футов = 1,057⋅10−13 световых лет = 6,67⋅10−9 а.
Сколько см в метре таблица?
Таблица мер измерения
| 1 т | тонна | 1 т = 10 ц = 1 000 кг = 106 г |
|---|---|---|
| 1 м | метр | 1 м = 10 дм |
| 1 дм | дециметр | 1 дм = 10 см = 0,1 м |
| 1 см | сантиметр | 1 см = 10 мм = 0,01 м |
| 1 мм | миллиметр | 1 мм = 1 000мк = 10-3 м |
•3 авг. 2020 г.
Что значит формула S VT?
S=v*t, где v — понятно что такое, S — расстояние, которое требуется найти, t — время, за которое объект прошел это расстояние. Таким образом вычисляется значение расстояния.
Как отмечается расстояние в геометрии?
Расстояние между двумя точками на координатной оси и замечание о его обозначении. Замечание . В геометрии и в школьной геометрии, в частности, принято обозначать одинаково и сам отрезок и его длину. Если имеется отрезок прямой, ограниченный точками А и В, то этот отрезок как геометрический объект обозначается АВ.
Задача 1
Пусть
один сборщик собирает картофель в ведро с одного рядка и затем высыпает его в мешок.
Требуется оценить величину суммарного расстояния R(Xм), которое нужно пройти сборщику, если мешок
располагается в точке рядка
с координатой Xм. Считать, что картофель уже извлечен на поверхность рядка.
Указание. Предварительно выполнить статистическое
наблюдение для детерминированной ситуации, когда в ведро помещается 10 кг картофеля,
в мешок – 4 ведра, а урожайность картофеля составляет 10 кг/пог.м.
Решение
1-й
этап.
Статистическое
наблюдение дает нам следующую таблицу
Таблица
1
|
Xм |
R(Xм) |
|
0 |
24 |
|
1 |
16 |
|
2 |
12 |
|
3 |
12 |
|
4 |
16 |
Установим
закономерность R(Xм)=F(Xм) графическим способом.
Мастер
функций à Точечная à
Готово
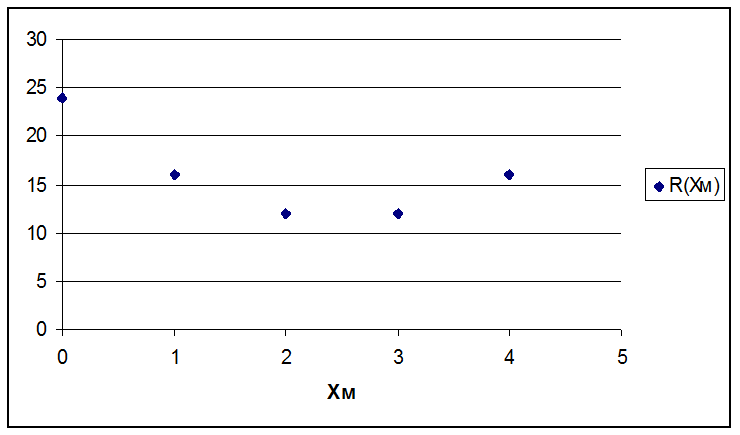
Рис. 1.
1ПМ
по эмпирической точке à Добавить линию тренда
Выбрать
тип “Полиномиальная” и перейти на вкладку Параметры.
Поставить птички, как показано на
рисунке и OK.
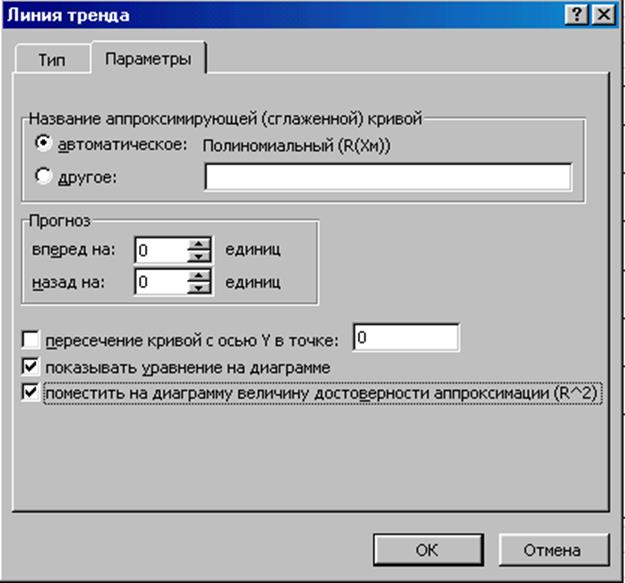
Рис.
2.
В результате получим (см. рис.
3).
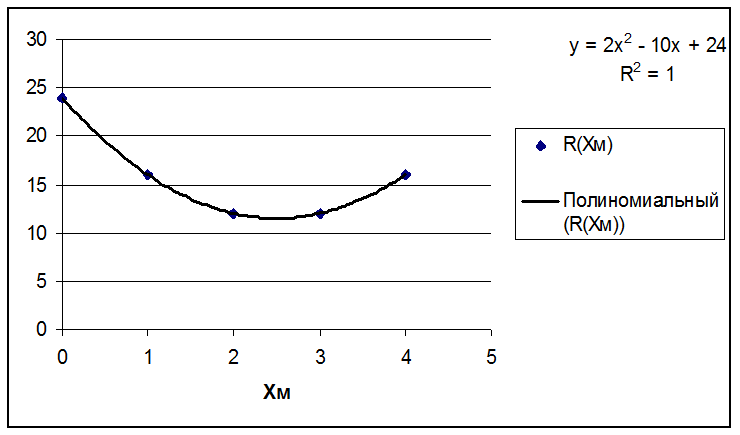
Рис.
3.
Таким образом, в результате
статистического наблюдения за процессом сбора картофеля в идеальном
(детерминированном) случае получили эмпирическую зависимость вида
R(Xм) = aX2 + bX +c,
где а = 2, b
= –10, c = 24.
Отсюда напрашивается вывод, что и
в общем (эконометрическом) случае – эта закономерность также будет иметь вид,
близкий к параболическому.
В лекции было показано, что
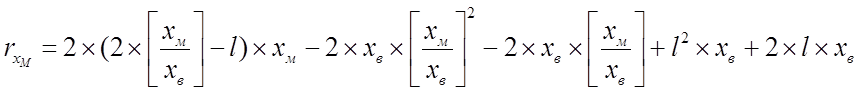 , (1)
, (1)
где Xв
– расстояние, которое нужно пройти, чтобы собрать одно ведро картофеля, l – емкость мешка […] – функция целой части числа.
2–й этап.
Считаем теперь урожайность
случайной величиной, которая приводит к тому, что модель для Xв
приобретает следующий (простейший) вид
![]() ,
,
где ![]() –
–
случайная величина, равномерно распределенная на отрезке [0, 1].
Оставляя предположение о емкости
мешка l = 4 ведра, и, используя функции Excel СЛЧИС() и ОКРУГЛ(), на основе соотношения (1) построим
таблицу, аналогичную таблице 1. Имеем табл. (2)
Таблица
2
|
Xм |
R(Xм) |
|
0 |
25,95 |
|
1 |
17,62 |
|
2 |
12,97 |
|
3 |
12,00 |
|
4 |
14,70 |
В табл. 2 вторая ячейка второго
столбца рассчитывается по формуле:
=2*(2*ОКРУГЛ(A28/(1+$F$28);0)-4)*A28-2*(1+$F$28)*ОКРУГЛ(A28/(1+$F$28);0)^2-2*(1+$F$28)*ОКРУГЛ(A28/(1+$F$28);0)+24*(1+$F$28),
где значение равномерно
распределенной случайной величины вычисляется в ячейке F28
по формуле =0,1*СЛЧИС(). Значения остальных ячеек второго столбца формируются
путем копирования.
В результате имеем (см. рис. 4)
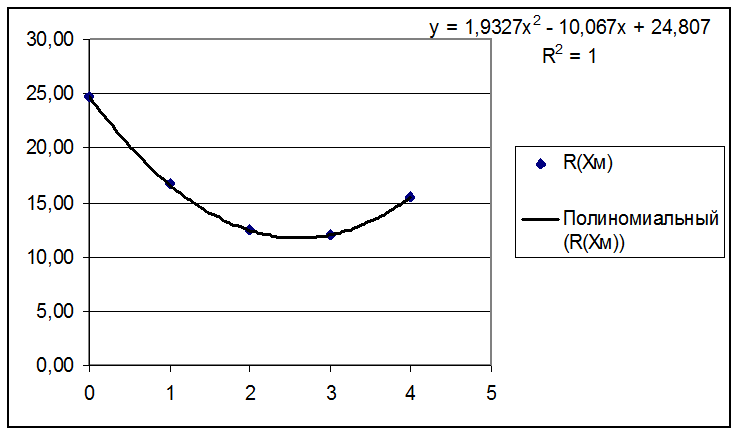
Рис.
4.
Необходимо заметить, что на
разных компьютерах расчеты конечной формулы для суммарного расстояния, которое
проходит сборщик картофеля, будут, вообще говоря, различными в силу аппаратных
особенностей.
Содержание
- суммарная длина
- Смотреть что такое «суммарная длина» в других словарях:
- Большая Энциклопедия Нефти и Газа
- Суммарная длина
- суммарная длина
- См. также в других словарях:
- суммарная длина
- Смотреть что такое «суммарная длина» в других словарях:
- Что значит суммарная длина
суммарная длина
Универсальный русско-английский словарь . Академик.ру . 2011 .
Смотреть что такое «суммарная длина» в других словарях:
Длина по фронту оползания, обрушения, оплывины — 21. Длина по фронту оползания, обрушения, оплывины протяженность уступов или борта карьера, подверженного разрушающей деформации. Измеряется наибольший размер нарушенного участка, повторяющий конфигурацию бровок откоса. В том случае, если… … Официальная терминология
Строительная длина кабельного изделия — 212. Строительная длина кабельного изделия Строительная длина Нормированная длина кабельного изделия в одном отрезке Примечание В котельную установку могут входить, кроме котла, тягодутьевые машины, устройства очистки поверхностей нагрева,… … Словарь-справочник терминов нормативно-технической документации
развернутая длина контактной сети (железной дороги) — Суммарная протяженность всех электрифицированных железнодорожных путей перегонов и станций в пределах предприятия железной дороги в целом или его отдельного структурного подразделения. [ГОСТ Р 53685 2009] Тематики электрификация, электроснабж.… … Справочник технического переводчика
РД 08.00-60.30.00-КТН-046-1-05: Неразрушающий контроль сварных соединений при строительстве и ремонте магистральных нефтепроводов — Терминология РД 08.00 60.30.00 КТН 046 1 05: Неразрушающий контроль сварных соединений при строительстве и ремонте магистральных нефтепроводов: 1.4.15 Бригада сварщиков группа аттестованных в установленном порядке сварщиков, назначенных… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 16332-70: Аппаратура колонная. Термины и определения — Терминология ГОСТ 16332 70: Аппаратура колонная. Термины и определения оригинал документа: 38. S образный элемент Часть тарелки из S образных элементов, выполненная из профилированного материала S образного сечения Определения термина из разных… … Словарь-справочник терминов нормативно-технической документации
Расшифровка снимков. — 4.4.19 Расшифровка снимков. 4.4.19.1 Снимки, допущенные к расшифровке, должны удовлетворять следующим требованиям: • длина каждого снимка должна обеспечивать перекрытие изображения смежных участков сварного соединения на величину не менее 20 мм,… … Словарь-справочник терминов нормативно-технической документации
СССР. Внутренние воды — Распределение воды рек, озёр, болот, водохранилищ, ледников, а также подземных вод по территории и особенности их режима определяются прежде всего климатическими факторами, балансом тепла и влаги. На территории СССР за год в среднем… … Большая советская энциклопедия
МЫШЦЫ — МЫШЦЫ. I. Гистология. Общеморфодогически ткань сократительного вещества характеризуется наличием диференцировки в протоплазме ее элементов специфич. фибрилярной структуры; последние пространственно ориентированы в направлении их сокращения и… … Большая медицинская энциклопедия
Транспорт в Канаде — Канада является экономически развитой страной с сильной индустрией добычи полезных ископаемых на обширной территории, занимающей второе место в мире после Российской Федерации. Транспортная система страны включает в себя более 1,1 миллиона… … Википедия
Пещера Снежная — Снежная Страна … Википедия
Автомагистрали Хорватии — Автомагистрали в Хорватии Автомагистрали в Хорватии. Автомобильный транспорт один из двух главных видов пассажирского транспорта в Хорватии (40,2 % пассажиров в 2010 году) … Википедия
Источник
Большая Энциклопедия Нефти и Газа
Суммарная длина
Суммарная длина по фронту в зависимости от мощности — от 1400 до 2400 мм, глубина — от 400 до 800 мм. [1]
Суммарная длина участков А. [2]
Суммарная длина L3 ( G) ребер, смежных только нефиксированным вершинам, которая определяется как суммарная длина ребер стандартного графа, построен-ногр на п — q вершинах, и оставшихся неучтенных ребер графа. [3]
Суммарная длина всех подпрограмм HIPACK составила на CDC-6500 5130 слов, в то время как решение задачи, связанной с заведением, заполнением и распечаткой одной одномерной и одной друхмерной гистограмм с использованием НВООК, эта система потребовала 11400 слов. Так как подпрограммы HIPACK независимы друг от друга, легко организовать их выполнение в оверлейном режиме, что позволит сократить объем требуемой памяти ЭВМ в несколько раз. Кроме того, в зависимости от вида решаемой задачи пользователь из пакета подпрограмм HIPACK может выбрать и использовать только те подпрограммы, которые ему нужны. [4]
Суммарная длина всех дефектов типа потеря металла составляет 833 098 м, что составляет 0 55 % протяженности обследованного участка трубопровода. Отсюда следует, что на болотах дефектов коррозии больше, чем на остальных участках. [6]
Суммарная длина горизонтальных участков труб должна быть не более 3 м, так как с увеличением их длины температура продуктов сгорания и величина тяги уменьшаются. [7]
Суммарная длина всех перпендикуляров, опущенных из любой точки, находящейся внутри равностороннего треугольника, на каждую из его сторон является величиной постоянной, равной его высоте. [9]
Суммарная длина трех отрезков, отсеченных на сторонах равностороннего треугольника прямыми, параллельными его сторонам, проведенными через любую точку внутри его, является величиной постоянной, равной длине стороны треугольника. [11]
Суммарная длина по фронту в зависимости от мощности — от 1400 до 2400 мм, глубина — от 400 до 800 мм. [12]
Суммарная длина светильников превышает длину помещения: необходимо или применить более мощные лампы ( у которых световой поток на единицу длины больше), или увеличить число рядов, или компоновать ряды из сдвоенных, строенных светильников. [13]
Суммарная длина светильников равна длине помещения: задача решается установкой непрерывного ряда светильников. [14]
Суммарная длина светильников меньше длины помещения: принимается ряд с равномерно распределенными вдоль него разрывами А, между светильниками. [15]
Источник
суммарная длина
1 суммарная длина
2 суммарная приведённая длина
3 суммарная характеристическая длина
См. также в других словарях:
Длина по фронту оползания, обрушения, оплывины — 21. Длина по фронту оползания, обрушения, оплывины протяженность уступов или борта карьера, подверженного разрушающей деформации. Измеряется наибольший размер нарушенного участка, повторяющий конфигурацию бровок откоса. В том случае, если… … Официальная терминология
Строительная длина кабельного изделия — 212. Строительная длина кабельного изделия Строительная длина Нормированная длина кабельного изделия в одном отрезке Примечание В котельную установку могут входить, кроме котла, тягодутьевые машины, устройства очистки поверхностей нагрева,… … Словарь-справочник терминов нормативно-технической документации
развернутая длина контактной сети (железной дороги) — Суммарная протяженность всех электрифицированных железнодорожных путей перегонов и станций в пределах предприятия железной дороги в целом или его отдельного структурного подразделения. [ГОСТ Р 53685 2009] Тематики электрификация, электроснабж.… … Справочник технического переводчика
РД 08.00-60.30.00-КТН-046-1-05: Неразрушающий контроль сварных соединений при строительстве и ремонте магистральных нефтепроводов — Терминология РД 08.00 60.30.00 КТН 046 1 05: Неразрушающий контроль сварных соединений при строительстве и ремонте магистральных нефтепроводов: 1.4.15 Бригада сварщиков группа аттестованных в установленном порядке сварщиков, назначенных… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 16332-70: Аппаратура колонная. Термины и определения — Терминология ГОСТ 16332 70: Аппаратура колонная. Термины и определения оригинал документа: 38. S образный элемент Часть тарелки из S образных элементов, выполненная из профилированного материала S образного сечения Определения термина из разных… … Словарь-справочник терминов нормативно-технической документации
Расшифровка снимков. — 4.4.19 Расшифровка снимков. 4.4.19.1 Снимки, допущенные к расшифровке, должны удовлетворять следующим требованиям: • длина каждого снимка должна обеспечивать перекрытие изображения смежных участков сварного соединения на величину не менее 20 мм,… … Словарь-справочник терминов нормативно-технической документации
СССР. Внутренние воды — Распределение воды рек, озёр, болот, водохранилищ, ледников, а также подземных вод по территории и особенности их режима определяются прежде всего климатическими факторами, балансом тепла и влаги. На территории СССР за год в среднем… … Большая советская энциклопедия
МЫШЦЫ — МЫШЦЫ. I. Гистология. Общеморфодогически ткань сократительного вещества характеризуется наличием диференцировки в протоплазме ее элементов специфич. фибрилярной структуры; последние пространственно ориентированы в направлении их сокращения и… … Большая медицинская энциклопедия
Транспорт в Канаде — Канада является экономически развитой страной с сильной индустрией добычи полезных ископаемых на обширной территории, занимающей второе место в мире после Российской Федерации. Транспортная система страны включает в себя более 1,1 миллиона… … Википедия
Пещера Снежная — Снежная Страна … Википедия
Автомагистрали Хорватии — Автомагистрали в Хорватии Автомагистрали в Хорватии. Автомобильный транспорт один из двух главных видов пассажирского транспорта в Хорватии (40,2 % пассажиров в 2010 году) … Википедия
Источник
суммарная длина
Универсальный русско-немецкий словарь . Академик.ру . 2011 .
Смотреть что такое «суммарная длина» в других словарях:
Длина по фронту оползания, обрушения, оплывины — 21. Длина по фронту оползания, обрушения, оплывины протяженность уступов или борта карьера, подверженного разрушающей деформации. Измеряется наибольший размер нарушенного участка, повторяющий конфигурацию бровок откоса. В том случае, если… … Официальная терминология
Строительная длина кабельного изделия — 212. Строительная длина кабельного изделия Строительная длина Нормированная длина кабельного изделия в одном отрезке Примечание В котельную установку могут входить, кроме котла, тягодутьевые машины, устройства очистки поверхностей нагрева,… … Словарь-справочник терминов нормативно-технической документации
развернутая длина контактной сети (железной дороги) — Суммарная протяженность всех электрифицированных железнодорожных путей перегонов и станций в пределах предприятия железной дороги в целом или его отдельного структурного подразделения. [ГОСТ Р 53685 2009] Тематики электрификация, электроснабж.… … Справочник технического переводчика
РД 08.00-60.30.00-КТН-046-1-05: Неразрушающий контроль сварных соединений при строительстве и ремонте магистральных нефтепроводов — Терминология РД 08.00 60.30.00 КТН 046 1 05: Неразрушающий контроль сварных соединений при строительстве и ремонте магистральных нефтепроводов: 1.4.15 Бригада сварщиков группа аттестованных в установленном порядке сварщиков, назначенных… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 16332-70: Аппаратура колонная. Термины и определения — Терминология ГОСТ 16332 70: Аппаратура колонная. Термины и определения оригинал документа: 38. S образный элемент Часть тарелки из S образных элементов, выполненная из профилированного материала S образного сечения Определения термина из разных… … Словарь-справочник терминов нормативно-технической документации
Расшифровка снимков. — 4.4.19 Расшифровка снимков. 4.4.19.1 Снимки, допущенные к расшифровке, должны удовлетворять следующим требованиям: • длина каждого снимка должна обеспечивать перекрытие изображения смежных участков сварного соединения на величину не менее 20 мм,… … Словарь-справочник терминов нормативно-технической документации
СССР. Внутренние воды — Распределение воды рек, озёр, болот, водохранилищ, ледников, а также подземных вод по территории и особенности их режима определяются прежде всего климатическими факторами, балансом тепла и влаги. На территории СССР за год в среднем… … Большая советская энциклопедия
МЫШЦЫ — МЫШЦЫ. I. Гистология. Общеморфодогически ткань сократительного вещества характеризуется наличием диференцировки в протоплазме ее элементов специфич. фибрилярной структуры; последние пространственно ориентированы в направлении их сокращения и… … Большая медицинская энциклопедия
Транспорт в Канаде — Канада является экономически развитой страной с сильной индустрией добычи полезных ископаемых на обширной территории, занимающей второе место в мире после Российской Федерации. Транспортная система страны включает в себя более 1,1 миллиона… … Википедия
Пещера Снежная — Снежная Страна … Википедия
Автомагистрали Хорватии — Автомагистрали в Хорватии Автомагистрали в Хорватии. Автомобильный транспорт один из двух главных видов пассажирского транспорта в Хорватии (40,2 % пассажиров в 2010 году) … Википедия
Источник
Что значит суммарная длина
Господа специалисты, подскажите как правильно считают суммарную длину дефектов?
Насколько помню с учкомбината, сумма должна складываться всех найденных дефектов, это и будит суммарная длина дефектов.
Но примеры с ГОСТ 7512-82 не получаются:
ПРИМЕРЫ СОКРАЩЕННОЙ ЗАПИСИ ДЕФЕКТОВ ПРИ РАСШИФРОВКЕ СНИМКОВ И ДОКУМЕНТАЛЬНОМ ОФОРМЛЕНИИ РЕЗУЛЬТАТОВ РАДИОГРАФИЧЕСКОГО КОНТРОЛЯ
1. На снимке обнаружены изображения пяти пор с диаметром 3 мм каждая, цепочки пор с длиной 30 мм и максимальными длиной и шириной пор в цепочке 5 и 3 мм, и шлакового включения с длиной 15 мм и шириной 2 мм.
Максимальная суммарная длина дефектов на участке снимка длиной 100 мм составляет 20 мм.
Запись в документации: 5П3; Ц30П5×3; Ш15×2; S20.
2. На снимке обнаружены изображения двух скоплений пор (длина каждого скопления 10 мм, максимальный диаметр пор 0,5 мм) и скопление шлаковых включений (длина скопления 8 мм, максимальная длина и ширина включений 2 и 1 мм).
Максимальная суммарная длина дефектов на участке снимка длиной 100 мм составляет 18 мм.
Запись в документации: 2С10П0,5; С8Ш2×1; S18.
3. На снимке обнаружены изображения двух непроваров длиной 15 мм каждый и трещины длиной 40 мм.
Запись документации: 2Н15; Т40.
4. На снимке обнаружены изображения пяти пор с диаметром 4 мм каждая и непровара длиной 20 мм.
Максимальная суммарная длина пор на участке снимка длиной 100 мм составляет 12 мм.
Запись в документации: 5П4; S12; Н20.
Что не так делаю объясните
За раннее всем благодарен.
Источник
Трансфер из:https://blog.csdn.net/lin00jian/article/details/51209715
В процессе анализа данных и интеллектуального анализа данных нам часто необходимо знать размер различий между людьми, а затем оценивать сходство и категорию людей. Наиболее распространенными являются корреляционный анализ в алгоритмах анализа данных, классификации и кластеризации при извлечении данных, таких как K-ближайшие соседи (KNN) и K-средних (K-средние). Конечно, есть много способов измерения индивидуальных различий. Я недавно обращался к соответствующей информации, и здесь перечислены здесь.
Чтобы облегчить следующие объяснения и примеры, давайте сначала сравним различия между индивидуумами X и индивидуумами Y. Все они включают характеристики измерений N, то есть X = (x1, x2, x3,… xn), Y = ( y1, y2, y3,… yn). Давайте посмотрим, какие методы могут быть использованы для измерения разницы между ними, которые в основном делятся на меры расстояния и меры сходства.
Мера расстояния
Измерение расстояния используется для измерения расстояния, на котором люди существуют в пространстве. Чем больше расстояние, тем больше разница между людьми.
Евклидово расстояние
Евклидово расстояние является наиболее распространенной метрикой расстояния, которая измеряет абсолютное расстояние между точками в многомерном пространстве. Формула выглядит следующим образом:

Поскольку расчет основан на абсолютных значениях характеристик каждого измерения, евклидовы меры должны гарантировать, что показатели каждого измерения находятся на одном уровне шкалы.Например, использование евклидова расстояния для индикаторов с разными единицами роста (см) и весом (кг) может сделать результаты недействительными ,
Расстояние Минковского
Расстояние Мина – это обобщение евклидова расстояния, которое является общим выражением нескольких формул измерения расстояния. Формула выглядит следующим образом:

Здесь значение p является переменной, и когда p = 2, получается указанное выше евклидово расстояние.
Манхэттен Расстояние
Манхэттенское расстояние получено из расстояния городского квартала и является результатом суммирования расстояний в нескольких измерениях, то есть формула измерения расстояния, полученная при p = 1 на расстоянии Ming выше, выглядит следующим образом:

Расстояние Чебышева
Расстояние Чебышева происходит от ходов королей в шахматах. Мы знаем, что шахматный король может сделать только один шаг в окружающих 8 клетках за раз. Если вы хотите перейти от A (x1, y1) к B ( x2, y2) Какие минимальные шаги необходимы? На самом деле, расстояние Чебышева, расширяющееся в многомерное пространство, является расстоянием Минга, когда р стремится к бесконечности:

Фактически, вышеупомянутое Манхэттенское расстояние, евклидово расстояние и расстояние Чебышева являются приложениями расстояния Минковского в особых условиях.
Махаланобис Расстояние
Поскольку евклидово расстояние не может игнорировать разницу в показателях индикатора, базовый показатель необходимо проанализировать перед использованием евклидова расстояния.Стандартизация данныхПосле нормализации, основанной на измерениях каждого индекса, другая метрика расстояния, Расстояние Махаланобиса, называется расстоянием Махаланобиса после использования евклидова расстояния.
Мера сходства
Мера сходства (подобия), которая вычисляет степень сходства между людьми. В отличие от меры расстояния, чем меньше значение меры сходства, тем меньше сходство между людьми, тем больше разница.
Косинусное сходство в векторном пространстве
Косинусное сходство использует косинус угла между двумя векторами в векторном пространстве как меру разницы между двумя индивидуумами. По сравнению с метрикой расстояния сходство косинусов больше сфокусировано на разнице в направлении двух векторов, чем на расстоянии или длине. Формула выглядит следующим образом:

Коэффициент корреляции Пирсона
То есть коэффициент корреляции r в корреляционном анализе вычисляют косинус-угол пространственного вектора для X и Y на основе их собственной общей нормализации соответственно. Формула выглядит следующим образом:

Коэффициент Жакара
Коэффициент Жакара в основном используется для вычисления сходства между индивидами символьных или логических измерений.Так как характерные атрибуты индивидов идентифицируются символическими или логическими значениями, невозможно измерить конкретное значение разницы, и только «это одно и то же»? Из-за этого результата коэффициент Жакара заботится только о соответствии характеристик, разделяемых между людьми. Если вы сравниваете коэффициенты подобия Жакара для X и Y и сравниваете только одно и то же число в xn и yn, формула выглядит следующим образом:

Скорректированное косинусное сходство
Хотя косинусное сходство можно использовать для изменения смещения между индивидуумами, но поскольку оно может различать только различия между индивидуумами, невозможно измерить разницу в значениях каждого измерения, что приведет к такой ситуации, как оценка контента пользователями , 5-балльная шкала, пользователи X и Y оценили оба контента как (1,2) и (4,5) соответственно. Используя косинусное сходство, результат равен 0,98. Оба очень похожи, но из рейтинга Кажется, что X не любит эти два содержания, но Y предпочитает его. Нечувствительность сходства косинусов к значению приводит к ошибке в результате. Если эту иррациональность необходимо исправить, появляется корректировка сходства косинусов, то есть во всех измерениях. Минус среднее значение, например, средние значения X и Y равны 3, затем корректируются до (-2, -1) и (1,2), а затем вычисляются с использованием косинусного сходства, чтобы получить -0,8, сходство Это отрицательно и разница не маленькая, но, очевидно, более реалистична.
Евклидово расстояние и косинусное сходство
Евклидово расстояние является наиболее распространенной мерой расстояния, в то время как косинусное сходство является наиболее распространенной мерой подобия. Многие меры расстояния и меры сходства основаны на деформации и производной этих двух, поэтому ниже приводится сравнение между ними. Различия в реализации и среде применения при измерении индивидуальных различий.
Посмотрите на разницу между евклидовым расстоянием и косинусным сходством с помощью трехмерной системы координат:

Из рисунка видно, что метрика расстояния измеряет абсолютное расстояние между точками в пространстве и напрямую связана с координатами положения каждой точки (то есть значением размера отдельного элемента). Сходство косинусов измеряет угол пространственного вектора. Это больше разница в направлении, чем в позиции. Если положение точки A остается неизменным, а точка B находится вдали от начала координатной оси в направлении исходного направления, то косинусное сходство cosθ в это время остается неизменным, поскольку включенный угол не изменяется, а расстояние между двумя точками A и B, очевидно, изменяется. В этом разница между евклидовым расстоянием и косинусным сходством.
В соответствии с соответствующими методами расчета и характеристиками измерения евклидова расстояния и косинусного сходства они применимы к различным моделям анализа данных: евклидово расстояние может отражать абсолютную разницу отдельных числовых характеристик, поэтому оно больше используется при необходимости расчета значения по измерениям. Анализ, который отражает различия, такие как использование индикаторов поведения пользователя для анализа сходства или разницы в пользовательской ценности, косинусное сходство больше для того, чтобы отличать разницу от направления, но оно не чувствительно к абсолютным значениям и больше используется для использования пользователя в контенте Подсчет баллов позволяет различать сходство и различие интересов пользователей и устраняет проблему несовместимости метрик между пользователями (поскольку косинусное сходство не чувствительно к абсолютным значениям).
Выше приведены некоторые виды и краткие сведения о мерах расстояния и подобия. При фактическом использовании выбор подходящей меры расстояния или меры подобия может завершить многие анализ данных и моделирование интеллектуального анализа данных. Ниже будут представлены соответствующие введения.
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:

Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
____ ч |
|
2. |
____ м |
12 м/с |
4 с |
|
3. |
132 м |
____ м/мин |
11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
15 часов |
|
2. |
48 м |
12 м/с |
4 с |
|
3. |
132 м |
12 м/мин |
11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
