Как найти суммарную кинетическую энергию системы - Сайт, где вы сможете решить свои вопросы

Кинетической энергией механической системы называется сумма кинетических энергий всех точек этой системы:

T = ∑m_kv_k²/2,

где m_k и v_k — масса и скорость k-й материальной точки, принадлежащей данной системе.

На основании теоремы Кёнига кинетическая энергия произвольной механической системы определяется по формуле

T = Mv_C²/2 + ∑ m_kv_kr²/2

где M — масса всей системы;
v_C — скорость центра масс системы;
m_k — масса k-й точки системы;
v_kr — относительная скорость k-й точки при движении её вокруг центра масс (т.е. v_k=v_C+v_kr).

Из этой формулы можно получить следующие частные случаи для твёрдого тела:

при поступательном движении тела
v_k= v_C , v_kr=0,

T = mv_C²/2;
при вращении тела вокруг оси, проходящей через его центр масс,
v_C=0 , v_kr= ω × r_k ,

T = ∑ m_kv_kr²/2 = Jω²/2,

где J — момент инерции тела относительно оси, проходящей в данный момент времени через центр масс;
ω — угловая скорость вращения тела;
в случае произвольного движения тела (например при плоскопараллельном движении)
T = mv_C²/2 + Jω²/2.

Примеры решения задач >
Работа силы >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Решение задач и лекции по технической механике, теормеху и сопромату

Источник

Кинетическая
энергия материальной точки — скалярная
положительная величина, равная половине
произведения массы точки на квадрат
ее скорости, т. е.
.

Кинетическая
энергия механической системы
— арифметическая
сумма кинетических энергий всех
материальных точек этой системы

Кинетическая
энергия системы, состоящей из п
связанных между собой тел,
равна арифметической сумме кинетических
энергий всех тел этой системы:

Теорема Кенига.
Кинетическая энергия механической
системы в общем случае ее движения равна
сумме кинетической энергии движения
системы вместе с центром масс и
кинетической энергии системы при ее
движении относительно центра масс:

где
—
скоростьk
– й точки
системы относительно центра масс.

Поступательное
движение.

При поступательном
движении тела

Вращение тела
вокруг неподвижной оси
.

где
– момент инерции тела относительно оси
вращения.

Плоскопараллельное
движение.

где
— момент инерции плоской фигуры
относительно оси, проходящей через
центр масс.

Задача
1.
Вычислить кинетическую энергию
однородного диска массы М
=10 кг,
катящегося без скольжения со скоростью
=
5м/с.

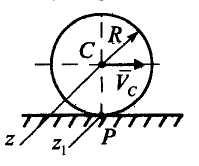
Решение.
Диск совершает плоскопараллельное
движение .

3. Теорема об изменении кинетической энергии точки

Теорема
в дифференциальной форме. Дифференциал
от кинетической энергии материальной
точки равен элементарной работе силы,
действующей на точку.

Доказательство:

Подставим в
выражение второго закона динамики

;

Теорема
интегральной (конечной) форме. Изменение
кинетической энергии материальной
точки на некотором перемещении равно
работе силы, действующей на точку, на
том же перемещении.

Доказательство

Дифференциал от
кинетической энергии точки равен
элементарной работе:

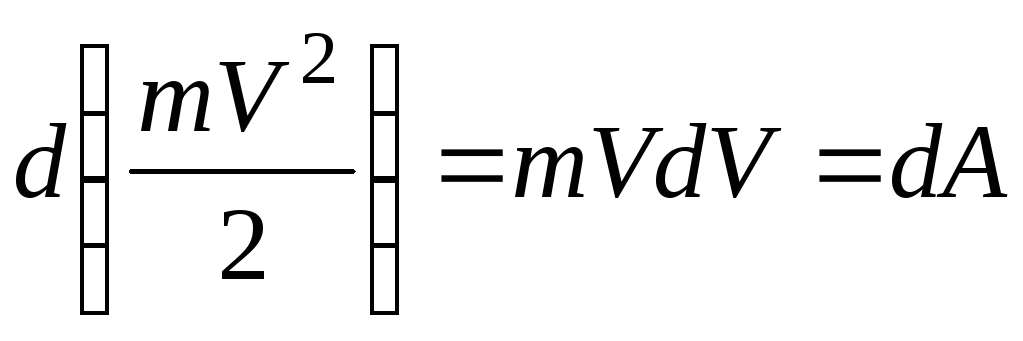Проинтегрируем

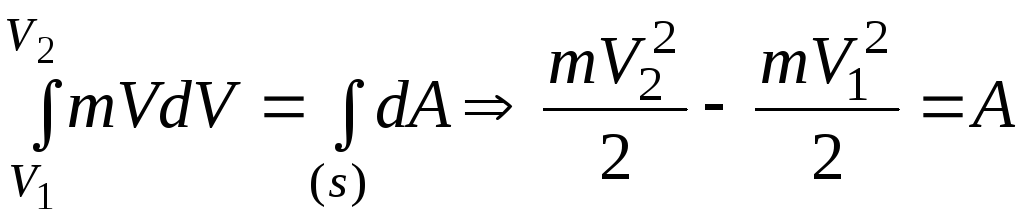4. Теорема об изменении кинетической энергии механической системы.

Теорема
в дифференциальной форме. Дифференциал
от кинетической энергии механической
системы равен сумме элементарных работ
внешних и внутренних сил, действующих
на систему.

Доказательство:
Для k
– й точки
системы

где
исоответственно — элементарная работа
внешней и внутренней сил, приложенных
кk–
й точке.

Для всей системы

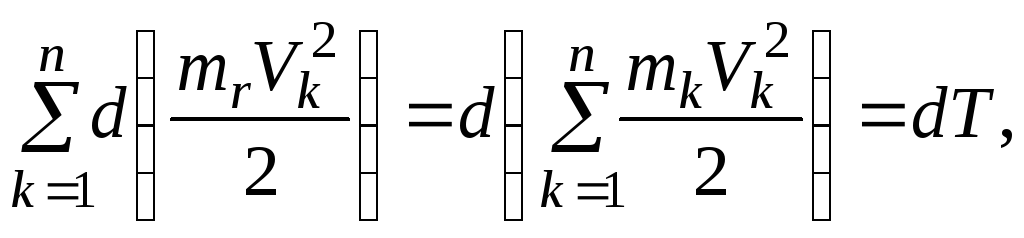
где
— кинетическая энергия системы;— соответственно элементарная работа
всех внешних и внутренних сил, приложенных
к системе. Таким образом,

Для системы твердых
тел

Тогда

Разделим на dt

где
— мощность внешних сил;— мощность внутренних. Тогда

Теорема
в интегральной (конечной) форме. Изменение
кинетической энергии механической
системы на некотором перемещении равно
сумме работ внешних и внутренних сил,
приложенных к системе, на том же
перемещении.

Доказательство:
Запишем теорему в интегральной форме
для k–
й точки системы:

где
и— соответственно работа внешней и
внутренней сил, приложенных кk-й
точке, на некотором перемещении.

Суммируя по всем
точкам системы, получим

Для системы твердых
тел
(по свойству внутренних сил). Тогда

Задача
2. Каток
А
приводится в движение из состояния
покоя посредством троса, который
одним концом намотан на каток, а вторым
— на барабан В.
Каток А
считать однородным цилиндром массы
= 50кг
и радиуса
= 0,4м.
Масса барабана
= 20кг
распределена по его ободу радиуса
= 0,2м.
К барабану приложен вращающий момент
= 100Нм.
Пренебрегая скольжением и трением
качения катка по горизонтальной плоскости
и весом троса, определить скорость
катка, когда он переместится на расстояние
s
= 2 м.

Решение.
Применим теорему об изменении кинетической
энергии механической системы в
интегральной форме:

где
— система движется из состояния покоя

—по свойству
внутренних сил. Тогда
..
КатокА
совершает плоскопараллельное движение.

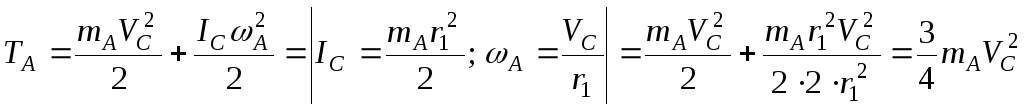Барабан В
совершает вращательное движение.

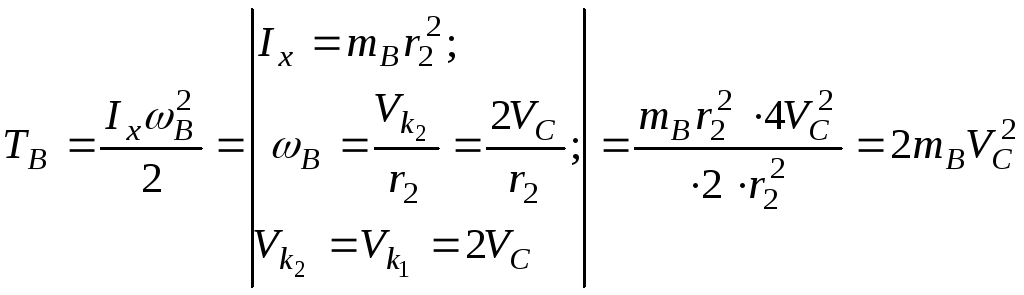Внешними силами
являются силы тяжести
,
нормальная реакция,
сила сцепления,
вращающий момент,
реакциии.

так как сила
;так как силаприложена в МЦС;так как;,,— точка приложения сил не перемещается.

,
где
.

Тогда

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Теоре́ма о кинети́ческой эне́ргии систе́мы — одна из общих теорем динамики^[1], является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел^[2]^[3].

Формулировка теоремы[править | править код]

Кинетической энергией системы называют сумму кинетических энергий всех тел, входящих в систему. Для определённой таким образом величины справедливо утверждение^[2]^[3]:

Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.

Теорема допускает обобщение на случай неинерциальных систем отсчёта. В этом случае к работе всех внешних и внутренних сил необходимо добавить работу переносных сил инерции (кориолисовы силы инерции не могут производить работу)^[4].

Доказательство теоремы[править | править код]

Рассмотрим систему материальных точек с массами m_i , скоростями vec v_i и кинетическими энергиями ${displaystyle T_{i}={frac {1}{2}}m_{i}{v_{i}}^{2}}$ .
Для малого изменения кинетической энергии (дифференциала), происходящего в течение некоторого малого промежутка времени будет выполняться

${displaystyle dT_{i}=m_{i}{vec {v}}_{i}d{vec {v}}_{i}=m_{i}{vec {v}}_{i}{frac {d{vec {v}}_{i}}{dt}}dt.}$

Учитывая, что ${displaystyle {frac {d{vec {v}}_{i}}{dt}}}$ представляет собой ускорение i-ой точки ${displaystyle {vec {a}}_{i}}$ , а ${displaystyle {vec {v}}_{i}dt}$ — перемещение той же точки ${displaystyle d{vec {s}}_{i}}$ за время , полученное выражение можно записать в виде:

${displaystyle dT_{i}=m_{i}{vec {a}}_{i}d{vec {s}}_{i}.}$

Используя второй закон Ньютона и обозначая равнодействующую всех сил, действующих на точку, как ${displaystyle F_{i}}$ , получаем

${displaystyle dT_{i}={vec {F}}_{i}d{vec {s}}_{i},}$

а затем в соответствии с определением работы ${displaystyle dA_{i}}$

${displaystyle dT_{i}=dA_{i}.}$

Суммирование всех уравнений такого вида, записанных для каждой из материальных точек, приводит к формуле для изменения полной кинетической энергии системы:

${displaystyle dT=sum limits _{i}dA_{i}.}$

Данное равенство выражает утверждение теоремы об изменении кинетической энергии системы в дифференциальном виде.

Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторыми $t_{1}$ и $t_{2}$ , получим выражение теоремы об изменении кинетической энергии в интегральной форме:

${displaystyle T_{2}-T_{1}=sum limits _{i}A_{i},}$

где ${displaystyle T_{1}}$ и ${displaystyle T_{2}}$ — значения кинетической энергии системы в моменты времени $t_{1}$ и $t_{2}$ соответственно.

Необходимо подчеркнуть, что здесь, в отличие от случаев теоремы об изменении количества движения системы и теоремы о движении центра масс системы, учитывается действие не только внешних, но и внутренних сил.

Закон сохранения механической энергии[править | править код]

Отдельный интерес представляют системы, в которых на тела действуют потенциальные силы^[5]. Для таких сил вводится понятие потенциальной энергии, изменение которой в случае одной материальной точки по определению удовлетворяет соотношению:

${displaystyle W_{2i}-W_{1i}=-A_{pi},}$

где ${displaystyle W_{1i}}$ и ${displaystyle W_{2i}}$ — значения потенциальной энергии точки в начальном и конечном состояниях соответственно, а ${displaystyle A_{pi}}$ — работа потенциальной силы, совершаемая при перемещении точки из начального состояния в конечное.

Изменение потенциальной энергии системы получается в результате суммирования изменений энергий всех тел системы:

${displaystyle W_{2}-W_{1}=-sum limits _{i}A_{pi}.}$

Если все внутренние и внешние силы, действующие на тела системы, потенциальны^[6], то

${displaystyle sum limits _{i}A_{i}=sum limits _{i}A_{pi}=-(W_{2}-W_{1}).}$

Подставляя полученное выражение в уравнение теоремы о кинетической энергии, получим:

${displaystyle T_{2}-T_{1}=-(W_{2}-W_{1})}$

или, что то же самое

${displaystyle T_{2}+W_{2}=T_{1}+W_{1}.}$

Иначе говоря, получается, что для полной механической энергии системы выполняется

Таким образом, можно сделать вывод:

Если на тела системы действуют только потенциальные силы, то полная механическая энергия системы сохраняется.

Данное утверждение и составляет содержание закона сохранения механической энергии, являющегося следствием теоремы о кинетической энергии и одновременно частным случаем общего физического закона сохранения энергии^[2]^[3].

Случай системы с идеальными стационарными связями[править | править код]

Основной источник: ^[7]

В тех случаях, когда предметом изучения является лишь движение системы, а реакции связей не представляют интереса, пользуются формулировкой теоремы для системы с идеальными стационарными связями, которая выводится с учетом принципа Даламбера-Лагранжа.

Теорема об изменении кинетической энергии системы с идеальными стационарными связями утверждает^[7]:

Дифференциал кинетической энергии системы с идеальными стационарными связями равен сумме элементарных работ на действительных перемещениях действующих внешних и внутренних сил

Теорема доказывается следующим образом. Заменяя в общем уравнении динамики ${displaystyle delta {vec {r}}_{k}}$ на ${displaystyle {vec {v}}_{k}dt}$ , получаем:

${displaystyle (sum m_{k}{vec {w}}_{k}){vec {v}}_{k}dt=sum {vec {F}}_{k}{vec {v}}_{k}dt}$

или

${displaystyle (dsum m_{k}{vec {v}}_{k}){vec {v}}_{k}=sum {vec {F}}_{k}^{ae}{vec {v}}_{k}dt+sum {vec {F}}_{k}^{ai}{vec {v}}_{k}dt}$

Поскольку ${displaystyle d{vec {v}}_{k}{vec {v}}_{k}=d{frac {v_{k}^{2}}{2}}}$ , получаем окончательно:

${displaystyle dT=d'A^{ae}+d'A^{ai}}$

Верхние значки в этих выражениях обозначают: ${displaystyle ^{a}}$ — активная (то есть не являющаяся реакцией связей) сила, ${displaystyle ^{e}}$ (от англ. external) и ${displaystyle ^{i}}$ (от англ. internal) — соответственно, внешняя и внутренняя сила.

См. также[править | править код]

Теорема о движении центра масс системы
Теорема об изменении количества движения системы

Примечания[править | править код]

↑ Тарг С. М. Динамика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 616-617. — 707 с. — 100 000 экз.
↑ ¹ ² ³ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 301-323. — 416 с. — ISBN 5-06-003117-9.
↑ ¹ ² ³ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 70-71. — 319 с. — ISBN 5-95052-041-3.
↑ Жирнов Н. И. Классическая механика. — Серия: учебное пособие для студентов физико-математических факультетов педагогических институтов. — М., Просвещение, 1980. — Тираж 28 000 экз. — с. 262
↑ Напомним, что силы называют потенциальными, если работа, совершаемая ими при перемещении материальной точки, определяется только начальным и конечным положениями точки и не зависит от выбора траектории.
↑ То есть, диссипативные силы отсутствуют.
↑ ¹ ² Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. — С. 221-223. — ISBN 5-06-003587-5

Источник

Энергия.

Работа.
Мощность.
Механическая энергия.
Кинетическая энергия.
Потенциальная энергия тела вблизи поверхности Земли.
Потенциальна яэнергия деформированной пружины.
Закон сохранения механической энергии.
Закон изменения механической энергии.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии – фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной – работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила vec F и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение vec s . Сила vec F не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

A=Fs . (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н cdot м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол alpha (рис. 2).

Разложим силу vec F на две составляющие: $vec F _{parallel }$ (параллельную перемещению) и $vec F _{perp }$ (перпендикулярную перемещению). Работу совершает только $vec F _{parallel }$ . Поэтому для работы силы vec F получаем:

$A=vec F _{parallel }s=Fcosalpha cdot s$ . Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол alpha , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

$alpha=180^{circ}, cos alpha=-1$ , и для работы силы трения получаем:

$A_{TP}=-F_{TP}s=-mu mgs$ ,

где – масса тела, – коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

Это позволяет вычислять работу через координаты данных векторов:

$A=F_{displaystyle x}s_{displaystyle x}+F_{displaystyle y}s_{displaystyle y}+F_{displaystyle z}s_{displaystyle z}$ .

Пусть на тело действуют несколько сил $vec F_{1},vec F_{2},..,vec F_{n}$ и vec F – равнодействующая этих сил. Для работы силы vec F имеем:

$A=vec F vec s=(vec F_{1}+vec F_{2}+...+vec F_{n})vec s=vec F_{1}vec s+vec F_{2}vec s+...+vec F_{n}vec s$ ,

или

$A=A_{1}+A_{2}+...+A_{n}$ ,

где $A_{1}, A_{2},...,A_{n}$ – работы сил $F_{1}, F_{2},...,F_{n}$ . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность – это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

$N=frac{displaystyle A}{displaystyle t}$ .

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт – это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью vec v . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил vec F .

За время тело совершит перемещение . Работа силы vec F будет равна:

Отсюда получаем мощность:

или

где alpha -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда vec F – сила “тяги” двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

N=Fv .

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

$K=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ ,

где – масса тела, – его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

$K=frac{displaystyle m_{displaystyle 1}v_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}+frac{displaystyle m_{displaystyle 2}v_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}+...+frac{displaystyle m_{displaystyle N}v_{displaystyle N}^{displaystyle 2}}{displaystyle 2}$ .

Если тело движется под действием силы vec F , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы vec F . Покажем это для случая прямолинейного равноускоренного движения.

Пусть $vec{v_{1}}$ – начальная скорость, $vec{v_{2}}$ – конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы vec F ). Для работы силы vec F получаем:

$A=vec{F}vec{s}=F_{x}s_{displaystyle s}=ma_{displaystyle x}s_{displaystyle x}= ma_{displaystyle x}frac{{v_{displaystyle 2x}}^{displaystyle 2}-{v_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}=frac{{displaystyle mv_{displaystyle 2x}}^{displaystyle 2}-{displaystyle mv_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2}$ .

(мы воспользовались формулой для $s_{x}$ , выведенной в статье “Равноускоренное движение”). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому ${v_{displaystyle 1x}}^{displaystyle 2}={v_{displaystyle 1}}^{displaystyle 2}$ и ${v_{displaystyle 2x}}^{displaystyle 2}={v_{displaystyle 2}}^{displaystyle 2}$ . В результате имеем:

$A=frac{displaystyle mv_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle mv_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}=K_{displaystyle 2}-K_{displaystyle 1}=Delta K$ ,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример – торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример – равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля $K_{displaystyle 1}=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ , конечная кинетическая энергия $K_{displaystyle 2}=0$ . Изменение кинетической энергии $Delta K=K_{displaystyle 2}-K_{displaystyle 1}=-frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ .

На автомобиль действуют сила тяжести m vec g , реакция опоры vec N и сила трения vec f . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

Из теоремы о кинетической энергии теперь получаем:

$Delta K=A Rightarrow - frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}=- mu mgs Rightarrow s=frac{displaystyle v^{displaystyle 2}}{displaystyle 2 mu g}$ .

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

W=mgh

где – ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте $h_{1}$ , в точку , находящуюся на высоте $h_{2}$ (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести m vec g и перемещением тела vec s обозначим alpha . Для работы силы тяжести получим:

Но, как видно из рис. 3, $s cos alpha=h_{1}-h_{2}$ . Поэтому

$A=mg(h_{1}-h_{2})=mgh_{1}-mgh_{2}$ ,

или

$A=W_{1}-W_{2}$ . (3)

Учитывая, что $W_{1}-W_{2}=-(W_{2}-W_{1})=- Delta W$ , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости . Начальная деформация пружины равна $x_{1}$ . Предположим,
что пружина деформируется до некоторой конечной величины деформации $x_{2}$ . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин $x_{1}$ и $x_{2}$ и определяется формулой:

$A=frac{kx_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle kx_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}$ .

Величина

$W=frac{displaystyle kx^{displaystyle 2}}{displaystyle 2}$

называется потенциальной энергией деформированной пружины (x – величина деформации).

Следовательно,

$A=W_{1}-W_{2}=- Delta W$ ,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

E=K+W .

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны $K_{1}$ и $W_{1}$ , в конечном положении – $K_{2}$ и $W_{2}$ . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

$K_{2}-K_{1}=A$ .

Но работа консервативных сил равна разности потенциальных энергий:

$A=W_{1}-W_{2}$ .

Отсюда получаем:

$K_{2}-K_{1}=W_{1}-W_{2}$ ,

или

$K_{1}+W_{1}=K_{2}+W_{2}$ .

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

$E_{1}=E_{2}$ .

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу $A_{TP}$ . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

$K_{2}-K_{1}=A+A_{TP}$ .

Но $A=W_{1}-W_{2}$ , следовательно

$K_{2}-K_{1}=W_{1}-W_{2}+A_{TP}$ .

Отсюда

$K_{2}+W_{2}-(K_{1}+W_{1})=A_{TP}$ ,

или

$E_{2}-E_{1}=A_{TP}$ .

В левой части стоит величина $Delta E=E_{2}-E_{1}$ – изменение механической энергии тела:

$Delta E=A_{TP}$ .

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Энергия.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Более наглядно не с автомобилями, а с глиной, которая от удара расплющивалась. Кинетическая энергия идет на пластическую деформацию + нагрев. Адам Савидж мерил штангенциркулем цилиндрические бруски глины и получил следующие данные:
a) удар в стальное бревно массой 1200 фунтов (545,5 кг); молот под углом 49° к вертикали:
длина бруска до удара = 2,68 дюйма, после удара = 1,5 дюйма;
b) удар в стальное бревно массой 1200 фунтов (545,5 кг); молот под углом 90° к вертикали: длина бруска до удара = 2,6 дюйма, после удара = 0,777 дюйма;
c) удар двух молотов с углов 49° от вертикали: длины брусков до удара = ? (предположим 2,64 и 2,64), после удара = 1,54; 1,288.
Таким образом деформации составят:
a)
b)
c) $$delta_{c1}=2,640 in. - 1,540 in. = 1,100 in.;$
$$delta_{c2}=2,640 in. - 1,288 in. = 1,352 in.$
Неясно, почему были выбраны углы 49° и 90°, ведь скорость в нижней точке в таком случае не в 2 раза выше. Но совершенно понятно, что если увеличить количество деформируемого материала в 2 раза, то суммарная энергия распределится примерно поровну.

Однако мне непонятны следующие 2 момента.
(1) Где здесь зависимость от системы отсчета? Если в варианте c) наблюдатель сидит на левом молоте, он увидит деформацию, отличную от деформации в системе, связанной с установкой? И вообще, откуда наблюдатель знает, в какой системе отсчета он находится, если располагает только скоростью сближения двух тел?
(2) Мысленно проведем эксперимент d.
d) удар двух молотов с углов 0° и 90° от вертикали: длины брусков до удара = 2,64 и 2,64 дюйма, после удара = ?.
Суммарная энергия в 2 раза больше, чем в случае c). Какие деформации увидит наблюдатель в системе отсчета, связанной с установкой?

Источник

Решение задач и лекции по технической механике, теормеху и сопромату

3. Теорема об изменении кинетической энергии точки

4. Теорема об изменении кинетической энергии механической системы.

Формулировка теоремы[править | править код]

Доказательство теоремы[править | править код]

Закон сохранения механической энергии[править | править код]

Случай системы с идеальными стационарными связями[править | править код]

См. также[править | править код]

Примечания[править | править код]

Энергия.

Работа.

Мощность.

Механическая энергия.

Кинетическая энергия.

Потенциальная энергия тела вблизи поверхности Земли.

Потенциальна яэнергия деформированной пружины.

Закон сохранения механической энергии.

Закон изменения механической энергии.

Вам также может понравиться

Пишет не поддерживается на вашем устройстве google play как исправить

Как исправить ошибки в журнале школьном

Как найти все фото на android

Добавить комментарий Отменить ответ