Как найти суммарную напряженность в точке

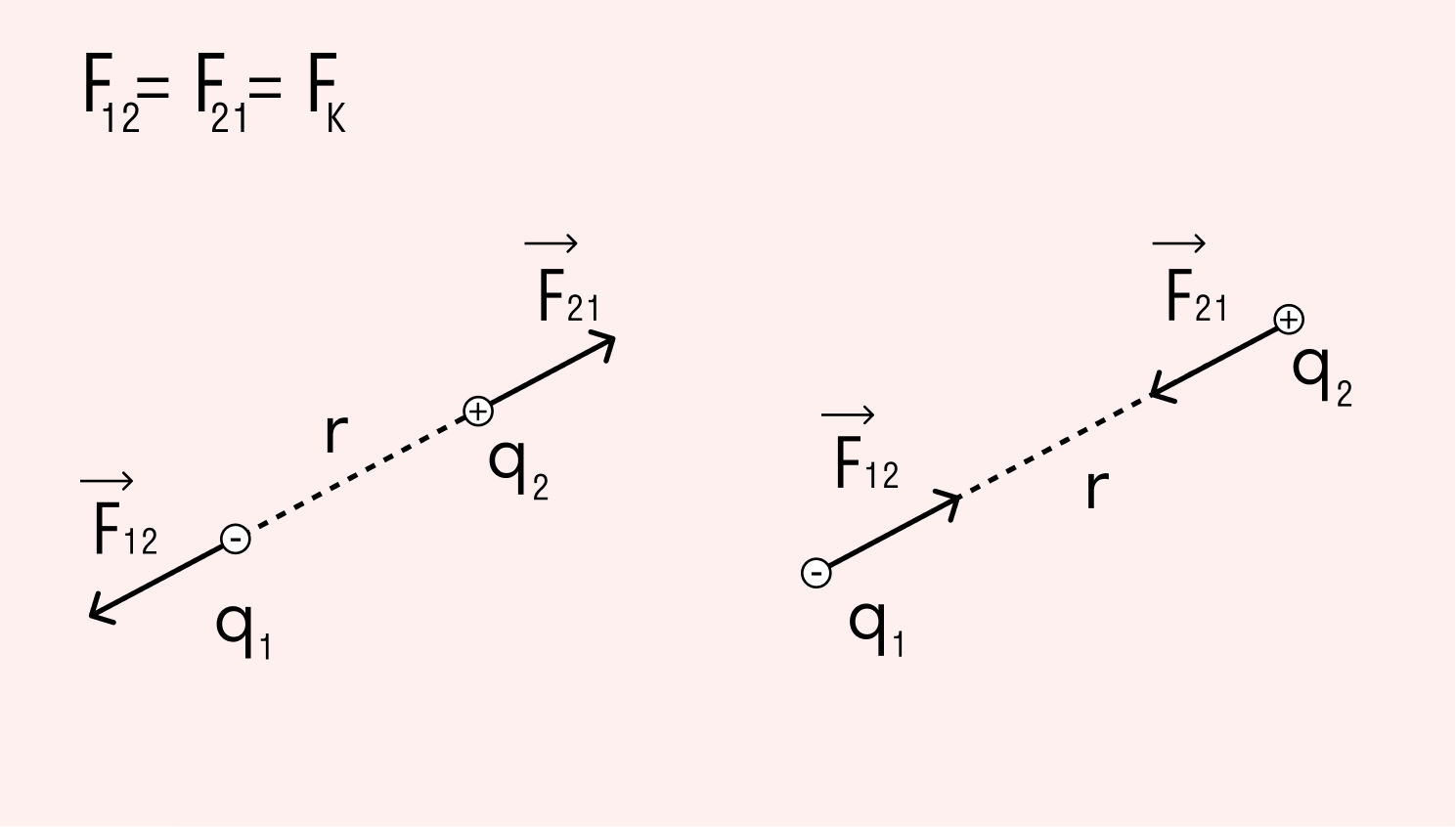
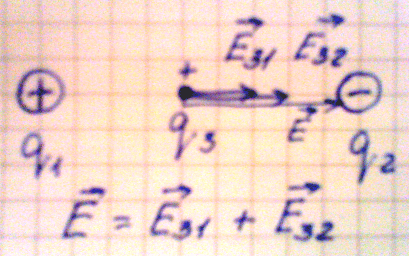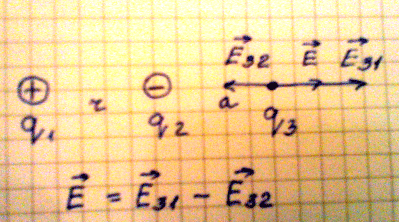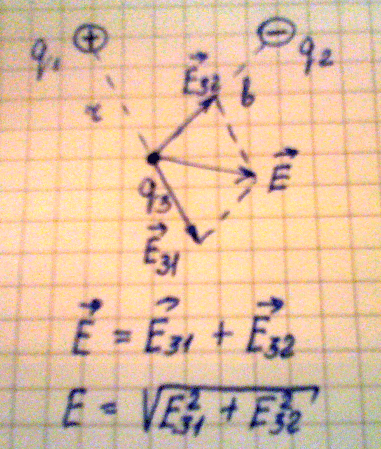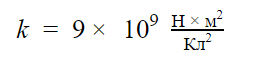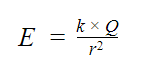Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.

Задачи урока:

• формирование понятия напряжённости электрического поля; дать понятие о
  линиях напряжённости и графическое представление электрического поля;
• научить учащихся применять формулу E=kq/r² в решении
  несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности
электрического поля:

1. нигде не пересекаются друг с другом;
2. имеют начало на положительном заряде (или в бесконечности) и конец на
   отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
3. между зарядами нигде не прерываются.

Рис.1

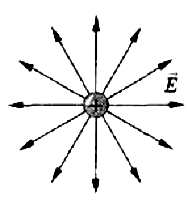
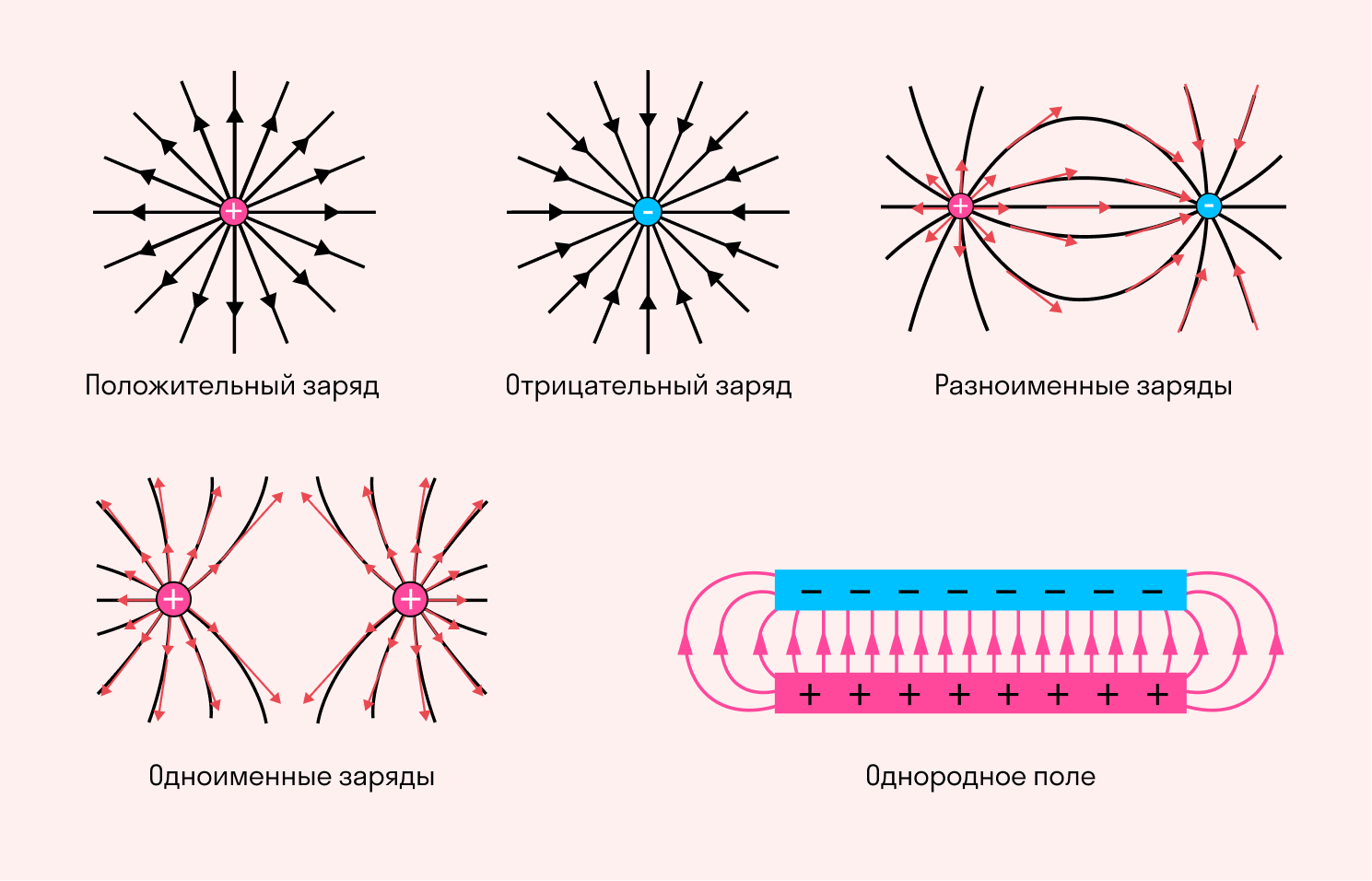
Силовые линии положительного заряда:

Рис.2

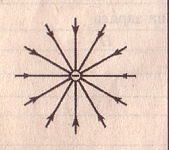
Силовые линии отрицательного заряда:

Рис.3

Силовые линии одноименных взаимодействующих зарядов:

Рис.4

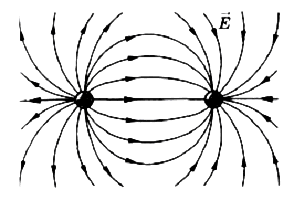
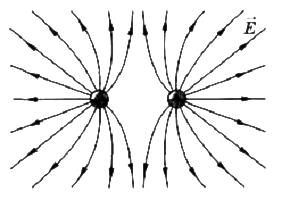
Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда

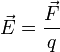
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.

В системе СИ
Н·м²/Кл²,

где ε₀ – электрическая
постоянная, равная 8,85·10^-12 Кл²/Н·м²;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:

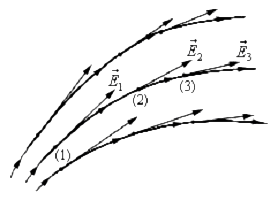
Рассмотрим несколько случаев определения напряженности.

1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

Е = kq₁/x² + kq₂/(r – x)²

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е₃₁ и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a)² – kq₂/a²

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Е = (Е₃₁² +Е₃₂²)^1/2

Следовательно:

Е = ((kq₁/r² )² + (kq₂/b²)²)^1/2

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

Проверочная работа.

Вариант № 1.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Вариант № 2.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Задачи на дом:

Законом Кулона описывается взаимодействие заряженных частиц. Однако большинство сил, с которыми мы работали, возникает при взаимодействии тел посредством контакта (т.е. тела касаются друг друга). В случае электромагнитного взаимодействия контакта нет, тогда взаимодействие происходит посредством неких невидимых элементов. Тогда взаимодействия между частицами вещества  и удалёнными друг от друга макроскопическими телами осуществляются через посредство физических полей, которые создаются этими частицами или телами в окружающем пространстве. В случае с заряженными частицами, эти поля назовём электромагнитными.

Тогда логика электромагнитного взаимодействия такова: заряд  создаёт вокруг себя электромагнитное поле, которое, в свою очередь, действует на любой другой заряд , находящийся на любом расстоянии от источника.

Закон Кулона описывает взаимодействие между двумя зарядами:

(1)

• где

Сила (1) зависит от обоих зарядов, что не позволяет толком описать электрическое поле, создаваемое каждым из взаимодействующих частиц. Тогда придумаем немного другую систему: возьмём пробный заряд  — некий малый заряд, который не будет искажать поле исследуемого нами заряда . Поместим пробный заряд в различные точки пространства рядом с исследуемым нами зарядом и проиллюстрируем силы Кулона (рис. 1).

В принципе, значение силы Кулона можно найти в любой точке пространства, однако данные силы зависят как от заряда источника, так и от значения пробного заряда. Введём новую переменную, поделив значение силы Кулона на значение пробного заряда:

(2)

• где
  • — вектор напряжённости электрического поля.

Подставим силу Кулона в (1):

(3)

Исходя из (3), можно заключить, что напряжённость электрического поля зависит от заряда источника поля и точки наблюдения, описываемой расстоянием от заряда (рис. 2).

Т.е. напряжённость электрического поля — параметр, описывающий поле, создаваемое зарядом-источником. Значение напряжённости электрического поля позволяет оценить сильно или слабо будет действовать поле на заряд, помещённый в него. Размерность  — В/м.

Исходя из (3), можно найти напряжённость поля точечного заряда. Напряжённость электрического поля — величина векторная, поэтому для её нахождения необходимо знать как модуль, так и направление вектора. Начнём с модуля:

(4)

Чтобы выяснить направление вектора, воспользуемся уравнением (2). Исходя из (2), можно заключить, что направление напряжённости электрического поля совпадает с направлением силы Кулона, а направление силы Кулона зависит от знака взаимодействующих зарядов. Чтобы не заморачиваться с рассмотрением этих зарядов в каждой задаче, просто договоримся. Если источник поля (заряд) положителен, тогда напряжённость поля направлена от заряда, если источник поля (заряд) отрицателен, тогда напряжённость поля направлена к заряду (рис. 3).

Напряжённость системы зарядов. Принцип суперпозиции напряжённости.

В случае, если в задаче источниками поля являются несколько зарядов, тогда напряжённость в интересующей точке можно найти как векторную сумму напряжённостей от каждого из зарядов:

(5)

Важно: поиск векторной суммы чаще всего сопряжён с реализацией теоремы Пифагора, теоремы косинусов или синусов, иногда с проецированиием векторов напряжённости на оси с последующим суммированием.

Проиллюстрируем: пусть в системе присутствует 3 заряда (, , ), найти напряжённость в точке А, находящейся на заданном расстоянии от каждого из них (, , ) (рис. 4).

Пользуясь знаниями о зарядах, расставляем направления напряжённостей от каждого из зарядов, значение модуля каждой из них можем найти из (4). А далее геометрически складываем, получая искомый .

Напряжённость поля бесконечной заряженной плоскости.

Отдельно в школьной физике рассматривается бесконечная (осень большая) заряженная равномерно плоскость (рис. 5).

Напряжённость такой плоскости вблизи её:

(6)

В (6) использовалось определение поверхностной плотности заряда:

(7)

Важно: напряжённость бесконечной плоскости не зависит от расстояния от плоскости.

Напряжённость поля двух бесконечных заряженных плоскостей (конденсатор).

Если составить систему из двух бесконечных плоскостей, заряженных одинаковым по модулю и различным по знаку зарядом (при этом площади плоскостей одинаковы), то общая напряжённость между ними:

(8)

Уравнение (8) характеризует напряжённость внутри конденсатора (рис. 6).

Вывод: в случае, если в задаче требуется найти напряжённость, она дана, достаточно рассмотреть систему. Различных систем, а соответственно, и формул, немного: точечный заряд, шар, система точечных зарядов и бесконечные плоскости. Для каждой системы — своё решение.

Что такое электрическое поле

Долгое время ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».

Тела, имеющие одноименные заряды, будут отталкиваться, а разноименные — притягиваться.

Определение напряженности электрического поля

Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.

Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.

Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q₁ поместить еще один точечный заряд q₂ (допустим, они оба будут положительными). Со стороны q₁ на q₂ будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление.

Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые заряженные объекты.

Единицы измерения и формулы

Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:

E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.

Если нужно выразить силу через напряженность, мы получим следующую формулу:

Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.

Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).

Принцип суперпозиции

Допустим, у нас есть несколько зарядов, которые взаимодействуют. Вокруг каждого существует свое электрическое поле. Тогда существует некая точка или область, в которой одновременно существует электрическое поле нескольких зарядов. Чему равна общая напряженность электрического поля, создаваемого этими зарядами?

Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав векторно напряженности, создаваемые каждым зарядом в отдельности в той же точке. Это и есть принцип суперпозиции.

Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:

• расстояние между зарядами очень мало — порядка 10^-15м;

• речь идет о сверхсильных полях с напряженностью более 10²⁰в/м.

Но задачи с такими данными выходят за пределы школьного курса физики.

Напряженность поля точечного заряда

У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.

Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.

Закон Кулона

Предположим, в вакууме есть два точечных заряда, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на них действуют силы, направленные вдоль соединяющей их прямой.

Силу электрического поля в конкретной точке можно найти по формуле: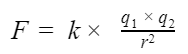 где q₁ и q₂ — модули точечных зарядов, r — расстояние между ними.

В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.

Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:

Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.

Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.

Линии напряженности

Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Рис. 3.1

Пример
1.
Два точечных электрических заряда Q₁
=
1нКл
и Q₂
=
-2 нКл
находятся
в воздухе на рас­стоянии d
= 10 см друг
от друга. Определить напря­женность
Е
и потенциал φ
поля, создаваемого этими зарядами в
точке А,
удаленной от заряда Q₁
на расстоя­ние r₁=
9 см и от
заряда Q₂
на r₂
= 7 см.
Определить также
силу F,
действующую в точке
А
на точечный заряд
Q
=10
нКл.

Решение.
Согласно принципу суперпозиции
элек­трических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность
электрического поля в искомой точке
может быть найдена как геометрическая
сумма напряженностей₁
и
₂
полей, создаваемых каждым зарядом в
отдельности:
.
Напряженности электриче­ского поля,
создаваемого в воздухе (ε=1)
зарядами Q₁
и Q₂,

;
.
(3.1)

Вектор
₁
(см. рис. 3.1) направлен по силовой линии
от заряда Q₁,
так как этот заряд положителен; вектор
₂
направлен также по силовой линии, но к
заряду Q₂,
так как этот заряд отрицателен.

Модуль
вектора
найдем по теореме косинусов:

,
(3.2)

где
– угол между векторами₁
и
₂,
,который
может
быть  найден  из  треугольника  со  сторонамиr₁,  r₂  и  d:

.
В данном случае во избежание громоздких
записей удобно значение cos α
вычислить отдельно:

.

Подставляя
выражение Е₁
и E₂
из (3.1) в (3.2) и вынося общий множитель
1/(4πε₀)
за знак корня, полу­чаем

. (3.3)

В
соответствии с принципом суперпозиции
электриче­ских полей, потенциал φ
результирующего
поля, созда­ваемого двумя зарядами
Q₁
и Q₂,
равен алгебраической сумме потенциалов:

φ=φ₁+φ₂. (3.4)

Потенциал
электрического поля, создаваемого в
ва­кууме точечным зарядом Q
на расстоянии r
от него, выра­жается формулой

. (3.5)

В нашем случае
согласно формулам (3.4) и (3.5) получим

,

или

.

Сила,
действующая на точечный заряд, находящийся
в электрическом поле в точке А

,

где напряженность
находится из выражения (3.3).

Произведем
вычисления:

;

.

П

Рис. 3.2.

ример 2. Три точечных
заряда Q₁=1
нКл, Q₂=
2 нКл и Q₃=
3 нКл расположены в вершинах
равностороннего треугольника, длина
стороны которого а= 5 см.
Определить напряженность поля в точке
А, находящейся
на пересечении биссектрис треугольника.

Решение.
Согласно принципу суперпозиции
элек­трических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность
электрического поля в искомой точке
может быть найдена как геометрическая
сумма напряженностей₁
и
₂
и
полей,
создаваемых каждым зарядом в отдельности:.
Напряженности электриче­ского поля,
создаваемого в воздухе (ε=1)
зарядами Q₁
и Q₂
и
Q₃:

; ;;.
(3.6)

Вектор
₁
(см. рис. 3.2) направлен по силовой линии
от заряда Q₁,
вектор
₂
направлен по силовой линии от заряда
Q₂
и вектор

₃
направлен
по силовой линии от заряда Q₃,
так как все заряды положительны.

Модуль
вектора
найдем из соотношения

,
(3.7)

где
и– проекции векторов_1
,2
и₃
на
координатные оси x
и y
(рис. 3.2).

,

.(3.8)

Подставляя
выражение Е₁
, Е₂
и E₃
из (3.6) в (3.8), получаем:

.
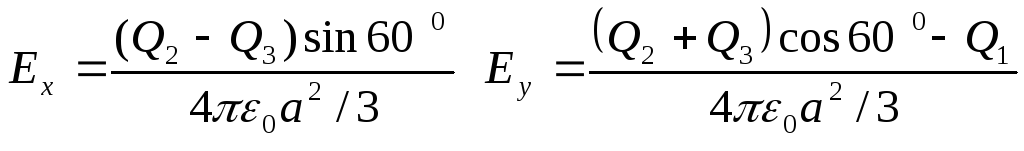
(3.9)

Модуль
вектора
находим, подставляя (3.9) в (3.7):.

Произведем
вычисления:

.

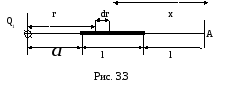
Пример
3. На тонком
стержне длиной l
= 10 см
нахо­дится равномерно распределенный
электрический заряд. На продолжении
оси стержня на расстоянии а
= 5 см от
ближайшего конца находится точечный
заряд Q₁=40
нКл, который
взаимодействует со стержнем с си­лой
F = 6 мкН.
Определить линейную плотность τ
заряда на стержне. Найти потенциал φ
в точке А,
расположенной на оси стержня и удаленной
от

его
ближайшего конца на расстояние l.

Решение.
Сила взаимодействия F
заряженного стержня с точечным зарядом
Q₁
зависит от линейной плотности τ
заряда на стержне. Зная эту зависимость,
можно определить τ.
При вычислении силы F
следует иметь в виду, что заряд на стержне
не является точеч­ным, поэтому закон
Кулона непосредственно применить
нельзя. В этом случае можно поступить
следующим образом. Выделим из стержня
(рис. 3.3) малый участок dr
с зарядом dQ
= τdr.
Этот заряд можно рассматривать как
точечный. Тогда, согласно закону Кулона:

.

Интегрируя
это выражение в пределах от а
до а+l,
получаем:

,

откуда

.

Проверим,
дает ли рас­четная формула единицу
линейной плотности электрического
заряда. Для этого в правую часть формулы
вместо символов величин подста­вим
их единицы:

Найденная единица
является единицей линейной плот­ности
заряда.

Произведем
вычисления:

.

Потенциал
dφ,
создаваемый точечным зарядом
в точке А (рис. 3.3), можно определить по
формуле

.

Согласно
принципу суперпозиции электрических
полей, потенциал электрического поля,
создаваемого заряженным стержнем в
точ­ке А, найдем интегрирова­нием
этого выражения:

.

Выполним
интегрирование:

.
(3.10)

Потенциал
в точке А по принципу суперпозиции
является суммой потенциалов, созданных
точечным зарядом
и стержнем с распределенным зарядом:,
где– потенциал в точке,
созданный зарядом;
а– потенциал в точке,
созданный стержнем и определяемый
выражением (3.10). Откуда

.

Подставим  числовые  значе­ния  физических  величин  в  СИ
(1/(4πε₀)=9^.10⁹
м/Ф,
Q₁=4^.
10^-8 Кл,
l=10^-1м,
а= 5^.10^-2
м, τ=10
^.10^-9
Кл/м)
и произведем вычис­ления:

φ=9
^.10⁹
(⁺1,25
^.10^-9
.0,693)=7,8
В.

Рис. 3.4

Рис.
3.4

Пример
4. По тонкой
нити, изогнутой по дуге окруж­ности,
равномерно распределен заряд с линейной
плот­ностью τ
= 10 нКл/м.
Определить напряженность
и потенциалφ
электрического поля, созда-ваемого
таким распределенным зарядом в точке,
совпадающей с цент­ром кривизны дуги.
Длина l
нити составляет ⅓ длины окружности и
равна 15 см.

Решение.
Выберем оси координат так, чтобы на­чало
координат совпадало с центром кривизны
дуги, а ось Оу была бы симметрично
расположена относительно концов дуги
(рис. 3.4). На нити выделим элемент длины
dl.
Заряд dQ=rdl,
находящийся на выделенном участке,
можно считать точечным.

Определим
напряженность электрического поля в
точке О. Для этого найдем сначала
напряженность dE
поля, создаваемого зарядом dQ:

,

где
– радиус-вектор, на­правленный от
элементаdl
к точке, в которой вычисляется
напряженность.

Выразим
вектор
через проекцииdE_x
и dE_y
на оси координат:

,

где
и– единичные векторы направлений (орты).
Напряженностьнайдем интегрированием:

.

Интегрирование
ведется вдоль дуги длиной l.
В силу симметрии
.
Тогда

, (3.11)

где
dE_y=dEcosθ=τdlcosθ/(4πε₀r²).
Так как r=R=const,
dl=Rdθ,
то

.

Подставим
выражение dE_y
в (3.11) и, приняв во внима­ние симметричное
расположение дуги относительно оси Оу,
пределы интегрирования возьмем от 0 до
π/3, а результат удвоим:

.

Выразив
радиус R
через длину l
нити (3l=2πR),
получим:

. (3.12)

Из
этой формулы видно, что напряженность
поля по направлению совпадает с осью
Оу.

Найдем
потенциал электрического поля в точке
О. Сначала найдем потенциал dφ,
создаваемый точечным зарядом dQ
в точке О:

.

Заменим
r
на R
и проведем интегрирование:

.

Так
как l
=
πR,
то
. (3.13)

Произведем
вычисления по формулам (3.12) и (3.13):

=2,17
кВ/м,

=188
В.

Рис. 3.5

Пример
5. По тон­кому
кольцу равномерно распределен заряд Q
= 50 нКл с
ли­нейной плотностью τ
= 40 нКл/м.
Опреде­лить напряженность Е
электрического поля, создаваемого этим
за­рядом в точке А, лежа­щей на оси
кольца и удаленной от его цен­тра на
расстояние, рав­ное половине радиуса.

Решение.
Совместим координатную плоскость хОу
с плоскостью коль­ца, а ось Oz – с осью
кольца (рис. 3.5). На кольце выделим малый
участок длиной dl.
Так как заряд dQ
= τ
dl, находящийся
на этом участке, можно считать точечным,
то напряженность

электрического поля, создаваемого этим
зарядом, может быть записана в виде

,

где
–
радиус-вектор, направленный от элементаdl
к точке А.

Разложим
вектор
на две
составляющие:
₁,
пер­пенди-кулярно плоскости кольца
(сонаправленную с осью Oz), и₂,
параллельную плоскости кольца (плос­кости
хОу), т.е.

=₁+₂.

Напряженность


электрического поля в точке А найдем
интегрированием:

,

где
интегрирование ведется по всем элементам
заряженно­го кольца. Заметим, что для
каждой пары зарядов dQ
и dQ’ (dQ=dQ’),
расположенных симметрично относительно
центра кольца, векторы dE₂
и dE₂’
в точке А равны по модулю и противоположны
по направлению:
₂=
–.
Поэтому векторная сумма (интеграл)
.
Состав­ляющиеdE₁
для всех элементов кольца сонаправлены
с осью Oz (единичным вектором
),
т.е.
₁=.
Тогда

.

Так
как
,и,
то

.

Таким образом,

.

Из
соотношения Q=2πRτ
определим радиус кольца:
.
Тогда

.

Модуль
напряженности
. (3.14)

Проверим,
дает ли правая часть полученного
равен­ства единицу напряженности,
В/м:

.

Выразим
физические величины, входящие в формулу
(3.14), в единицах СИ (τ=5^.10^-8
Кл/м,
Q=4^.10^-8Кл,
ε₀=8,85^.10^-12Ф/м)
и произведем вычисления:

.

Пример
6. Две
концентрические проводящие сферы
радиусами R₁=5
см и R₂
= 10 см
несут соответственно заряды Q₁
= 10 нКл
и Q ₂=-5
нКл. Найти
напряжен­ность Е
поля в точках, отстоящих от центра сфер
на рас­стояниях r₁
= 4 см,
r₂
= 8 см,
r₃
= 15 см.
Построить график Е(r).

Решение.
Заметим, что точки, в которых требуется
найти напряженности электрического
поля, лежат в трех областях (рис. 3.6):
обла­сти /(r₁<R₁),
области //(R₁<r₂<R₂),
области /// (r₃>R₂).

1. Для
определения на­пряженности Е₁
в области / проведем гауссову повер­хность
S₁
радиусом r₁
и воспользуемся теоремой Остроградского
– Гаусса:

(так
как суммарный заряд, находящийся внутри
гауссо­вой поверхности, равен нулю).
Из соображений симметрии E_n=E₁=const.
Следовательно,
иЕ₁
(напря­женность поля в области /) во
всех точках, удовлетворяю­щих условию
r₁<R₁,
будет равна нулю.

Рис. 3.6

2.
В области // гауссову поверхность проведем
радиу­сом r₂.
В этом случае диэлектрическую проницаемость
среды будем считать равной единице
(вакуум) и воспользуемся теоремой
Остроградского– Гаусса:

(так
как внутри гауссовой поверхности
находится только заряд Q₁).

Так
как Е_n=Е₂=const,
то Е можно
вынести за знак интеграла:

,
или
;

,

где
S₂=4πr₂²
– площадь гауссовой поверхности. Тогда

.
(3.15)

3.
В области /// гауссова поверхность
проводится ра­диусом r₃.
Обозначим напряженность E
области /// через Е₃
и учтем, что в этом случае гауссова
поверхность охватывает обе сферы и,
следовательно, суммарный заряд бу­дет
равен Q₁+Q₂.
Тогда

.

Заметив,
что Q₂<0,
это выражение можно переписать в виде

. (3.16)

Убедимся
в том, что правая часть равенств (3.15) и
(3.16) дает единицу напряженности:

. Выразим все величины в единицах СИ (Q₁
= 10^-8
Кл, Q₂
= —
5^.10^-9
Кл, r₁
= 0,08 м,
r₃
= 0,15 м,
1/(4πε₀)
= 9^.10⁹
м/Ф)
и произведем вычисления:

;

.

Построим
график Е(r).
В области / (r₁<R₁)
Е=0.
В области // (R₁≤r₂<R₂)
E₂(r)
изменяется по закону
.
В точкеr=R₁
напряженность E₂(R₁)
=

=36 кВ/м. В
точке r=R₂
(r стремится к R₂
слева) E₂(R₂)==
9 кВ/м.
В области /// (r>R₂)
E₃(r)
изменяется по закону
,
причем в точкеr=R₂
(r стре­мится к R₂
справа) E₃(R₂)
=

= 4,5 кВ/м.
Таким образом, функция Е(r)
в точках r=R₁
и r=R₂
терпит раз­рыв. График зависимости
E(r)
представлен на рис. 3.7.

Пример
7. В вакууме
имеется скопление зарядов в форме
длинного цилиндра радиуса R₀
= 2 cм.
Объемная
плотность зарядов
постоянна и равна2
мкКл/м³.
Найти напряженность поля в точках 1 и
2, лежащих на расстояниях r₁
= 1 cм,
r₂
= 3 cм
от оси цилиндра, и разность потенциалов
между этими точками. Построить графики
и.

Поле
создано зарядом, р

РРРИ

Рис.
3.8.

Рис.
3.8

авно-мерно распределенным по объему.
Конфигурация зарядов позволяет считать,
что поле обладает осевой симметрией:
силовые линии – прямые и в любой
плоскости, перпендикулярной оси цилиндра,радиальны
(рис. 3.8).

Вспомогательной
поверхности следует придать форму
цилиндрической поверхности, коаксиальной
заряду. Длина этого цилиндра может быть
произвольной, но заведомо много меньше,
чем длина заряженного цилиндра. Характер
функциональной зависимости
для точек, лежащих внутри и вне объемного
заряда, различен. Поэтому следует
провести две вспомогательные цилиндрические
поверхностиS₁
и S₂
с радиусами
и.

Определим
проекцию вектора E
на нормаль выбранной поверхности
Е_n1=E=const
и E_n2=0.
Поток через выбранную поверхность
цилиндра равен

(3.17)

где
h
– высота цилиндра.

Определим
заряд, попадающий внутрь выделенной
поверхности: при r<R₀

,
а приr>R₀

.
(3.18)

Применим
теорему Гаусса
,
используя выражение (3.17) и (3.18),
откуда

–напряженность
внутри цилиндра (3.19)

,
откуда

–напряженность
вне цилиндра. (3.20)

Для
определения разности потенциалов между
точками 1
и 2
разобьем 
на два интеграла: в пределах от точки 1
до поверхности, ограничивающей объемный
заряд, и от этой поверхности до точки
2:.
В первый интеграл следует подставлять
выражение  (3.19),  во  второй  выражение
(3.20):.
(3.21)

Подставляя
в (3.19) r=r₁
и в (3.20) r=r₂,
находим:

;

.

Вычислим численное
значение выражения (3.21):

.

Для
построения графика E_r(r)
на основании выражений (3.19) и (3.20)
целесообразно сначала рассчитать E_r
при r=R₀:

В/м.

Графическая
зависимость E_r(r)
показана на рис. 3.9.

График
зависимостиможно построить из анализа графикаE_r(r),
учитывая, что
.
Выберем начало отсчета на оси объемного
заряда:(0)=0.
Так как во всей области E_r>0,
т.е. (d/dr)<0,
то потенциал непрерывно убывает. В
области r<R₀
E_r
возрас-

тает

,
соответственно
и график(r)
обращен вогнутостью вниз. При
r>R₀
E_r
убывает
, соответственно

и график(r)
обращен вогнутостью вверх.

При
r=R₀
кривая (r)
имеет точку перегиба (вторая производная
изменяет знак). График (r)
изображен на рис. 3.10. Если изменить
начало отсчета потенциала, то характер
графика не изменяется, например, при
выборе начала отсчета на поверхности
объемного заряда
график примет вид, изображенный на рис.
3.10 пунктиром.

Пример
8. Электрическое
поле создается двумя зарядами Q₁
=2 мкКл
и Q₂
= -4 мкКл,
находящимися на расстоянии а=
0,2 м друг от
друга. Определить ра­боту A_1,2
сил поля по перемещению заряда Q=50
нКл из точки
1 в точку 2
(рис. 3.11).

Решение.
Для определения работы A_1,2
сил поля воспользуемся соотношением
A_1,2
=
Q(φ₁–φ₂).

Рис. 3.11

Применяя
принцип суперпозиции электрических
полей, определим по­тенциалы φ₁
и φ₂
точек 1 и
2 поля:

;

.

Тогда

,

или

.

Проверим, дает ли
правая часть равенства единицу работы
(Дж):

.

Подставим
числовые значения физических величин
в СИ:

(Q=50
^.10^-9Кл,
Q₁=2^.10^-6Кл,
Q₂=
4^.10^-6Кл,
a= 0,2 м,
)
и произведем вычис­ления:

.

Пример
9. Определить
ускоряющую разность потен­циалов U,
которую должен пройти в электрическом
поле электрон, обладающий скоростью
v₁=3^,10⁶м/с,
что­бы скорость его возросла в n
= 3 раза.

Решение.
Ускоряющую разность потенциалов можно
найти, вычислив работу А
сил электростатиче­ского поля. Эта
работа определяется произведением
эле­ментарного заряда е
на разность потенциалов U:

A=eU. (3.22)

Работа
сил электростатического поля в данном
слу­чае равна изменению кинетической
энергии электрона:

, (3.23)

где
Т₁
и Т₂
– кинетическая энергия электрона до и
после прохождения ускоряющего поля; m
– масса элект­рона; v₁
и v₂
– начальная и конечная скорости его.

Приравняв
правые части равенств (3.22) и (3.23), получим:

,
где
.

Отсюда
искомая разность потенциалов
.

Произведем
вычисления:

=
204,7 В.

Рис. 3.12

Пример
10.
С поверхности бесконечного равномерно
заряженного
(τ = 50 нКл/м)
прямого цилиндра вылетает α-частица
(v₀
= 0).
Определить кинетическую энергию T₂
α-частицы (кэВ)
в точке 2 на расстоянии 8R
от поверх­ности цилиндра (рис. 3.12).

Решение.
Так как силы электростатического поля
являются консервативными, то для
определения кинети­ческой энергии
α-частицы в точке 2 воспользуемся зако­ном
сохранения энергии, записанном в виде
W₁=W₂,
где W₁
и W₂
– полные
энергии α-частицы в точках 1 и 2.

Так
как W₁=T₁+U₁
и W₂=T₂+U₂
(T₁
и Т₂
– кине­тические энергии α-частицы;
U₁
и U₂
– потенциальные) , то, учитывая, что Т₁=0
(v₀=0),
можно записать U₁=T₂+U₂,
откуда Т₂=U₁-U₂=Q(φ₁-φ₂)
(Q
– заряд α-частицы; φ₁
и φ₂
– потенциалы точек 1 и 2).

Для
определения разности потенциалов
воспользуемся соотношением между
напряженностью по­ля и изменением
потенциала: Е=-gradφ.
Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение
можно записать в виде

,
или dφ=-Edr.

Интегрируя
это выражение, найдем разность
потен­циалов двух точек, отстоящих
на расстояниях r₁
и r₂
оси цилиндра:

. (3.24)

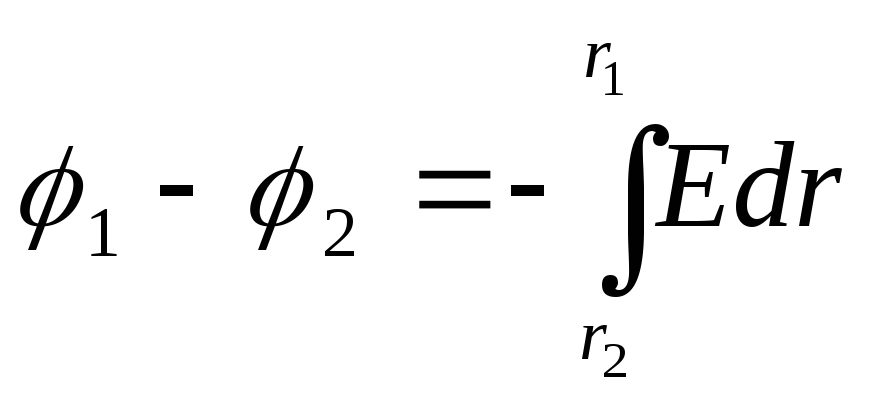
Так как цилиндр
длинный и точки взяты вблизи его средней
части, то для выражения напряженности
поля можно воспользоваться формулой
напряженности поля, создаваемого
бесконечно длинным цилиндром:

.

Подставив
это выражение в (3.24), получим:

.

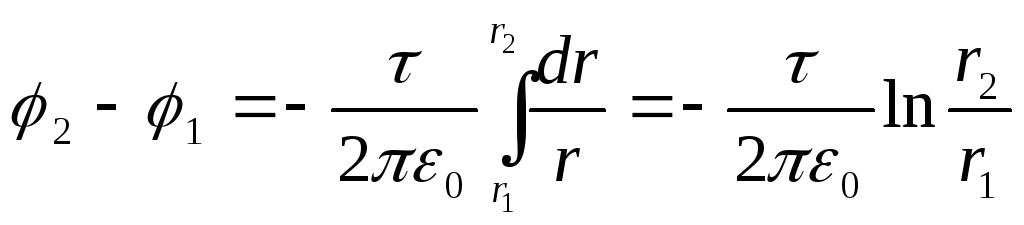
Учитывая,
что,
а,
запишем

.

Тогда

.

Выразим
все величины в единицах СИ (Q= 2^.1,60^.10^-19
Кл, τ= 50^.10^-9
Кл/м,
)
и произведем вычисления (—
коэффициент перевода из Дж
в эВ):

= = 3,96 кэВ.

Пример
11. Конденсатор
емкостью С₁=6
мкФ был
заряжен до разности потенциалов U₁=20
В. После
отключения от источника тока конденсатор
соединили параллельно с другим
незаряженным конденсатором емкостью
С₂=10
мкФ. Какая
энергия W’
израсходуется на образование искры в
момент присоединения второго конденсатора?

Решение.
Энергия, израсходованная на образо­вание
искры:

W’=W₁–W₂, (3.25)

где
W₁
– энергия, которой обладал первый
конденсатор до присоединения к нему
второго конденсатора; W₂
– энергия, которую имеет батарея,
составленная из двух конденсаторов.

Энергия заряженного
конденсатора определяется по формуле

W=½CU², (3.26)

где
С – емкость
конденсатора или батареи конденса­торов.

Выразив
в формуле (3.25) энергии W₁
и W₂
по фор­муле (3.26) и приняв во внимание,
что общая емкость параллельно соединенных
конденсаторов равна сумме емкостей
отдельных конденсаторов, получим

W’=½C₁U₁²-½(C₁+C₂)U₂², (3.27)

где
U₂
– разность потенциалов на зажимах
батареи конденсаторов.

Учитывая,
что заряд после присоединения второго
конденсатора остался прежним, выразим
разность потен­циалов U₂
следующим образом:

.

Подставив
выражение U₂
в (3.27)), найдем

,

или

.

Произведем
вычисления:

Дж=750
мкДж.

Пример
12. Потенциометр
сопро­тивлением R=150
Ом подключен к батарее с ЭДС
=300
В и внутрен­ним
сопротивлением R_i
= 50
Ом. Определить:
1) показание вольтметра сопротивлением
R_V
= 500 Ом,
соединенного с одной из клемм потенциомет­ра
и подвижным контактом, установленным
посередине потенциометра; 2) разность
потенциалов между теми же точками
потенциометра при отключении вольтметра.

Решение.
1. Показание вольтметра, подключенно­го
к точкам A
и В (рис. 3.13), определим по формуле

U₁=I₁R_1,

гдеR₁
– сопротивление параллельно соединенных
вольт­метра и половины потенциометра;
I₁
– суммарная сила тока в ветвях этого
соединения (она равна силе тока в
неразветвленной части цепи).

Силу
тока I₁
найдем по закону Ома для полной цепи:

I₁=/(R_e+R_i), (3.28)

где
R_e
– сопротивление внешней цепи. Это
сопротивле­ние есть сумма двух
сопротивлений:

R_e=R/2+R₁. (3.29)

Сопротивление
R₁
найдем по формуле параллельного
соединения проводников
,
откуда

Подставив
в (3.28) выражение R_e
по (3.29), найдем

.

В
данном случае решение задачи в общем
виде было бы громоздким. Поэтому удобно
вычисление величин провести раздельно:

=
65,22 Ом;

=
1,58 A;

U₁=1,58
^.65,22
= 103,04 B.

2.
Разность потенциалов между точками А
и В при отключенном вольтметре равна
произведению силы тока I₂
на половину сопротивления потенциометра:

,
(3.30)

где
I₂
– сила тока в цепи при отключенном
вольтметре. Ее определим по формуле

.

Подставив
выражение I₂
в (3.30), найдем

.

Произведем
вычисления:

=
112,5 В.

П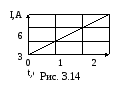ример
13. Сила тока
в проводнике сопротивлением R=20
Ом нарастает
в течение времени Δt
=2 с по
линей­ному закону от I₀=0
до I=6
А (рис. 3.14). Определить теплоту Q₁,
выделившуюся в этом проводнике за первую
секунду, и Q₂
– за вторую, а также найти отношение
.

Решение.
Закон Джоуля–Ленца в виде Q=I²Rt
справедлив для постоянного тока
(I=const).
Если же сила тока в проводнике изменяется,
то указанный закон справедлив для
бесконечно малого интервала времени и
записывается в виде

dQ=I²Rdt. (3.31)

Здесь
сила тока I
является некоторой функцией вре­мени.
В данном случае

I=kt,
(3.32)

где
k
— коэффициент про­порциональности,
характе­ризующий скорость измене­ния
силы тока:

.

С
учетом (3.32) формула (3.31) примет вид

dQ=k²Rt²dt. (3.33)

Для
определения теплоты, выделившейся за
конечный интервал времени Δt,
выражение (3.33) надо проинтегриро­вать
в пределах от t₁
до t₂:

.

Произведем
вычисления:

Q₁=^.
3^2
.20(1-0)=60
Дж;

Q₂=^.3^2.20(8-1)=420
Дж.

Следовательно,

,

т.е.
за вторую секунду выделится теплоты в
семь раз больше, чем за первую.

Для школьников.

Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.

Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.

В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).

Применим принцип суперпозиции для проекций указанных векторов на оси х и у:

Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.

Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.

В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:

В точке В результирующее поле направлено влево и равно:

В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:

Ответ: 36000 В/м; 3400 В/м; 4500 В/м.

Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.

Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:

Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:

Косинус угла найдём отдельно из треугольника образованного расстояниями:

Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.

Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Нахождение напряжённости электростатического поля.

Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.

Ссылки на другие занятия (до электростатики) даны в Занятии 1.

Ссылки на занятия (начиная с электростатики) даны в Занятии 45.