Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
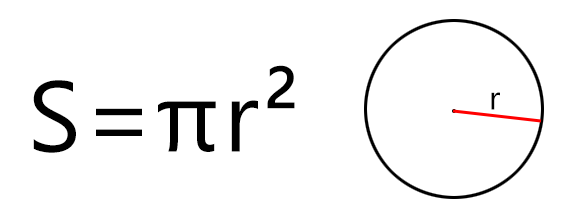
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
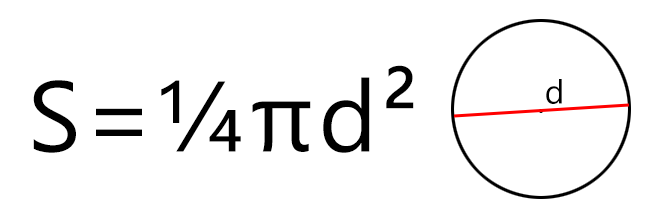
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
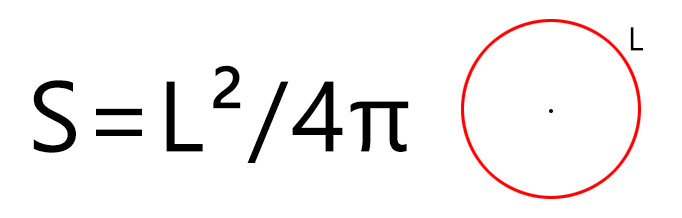
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
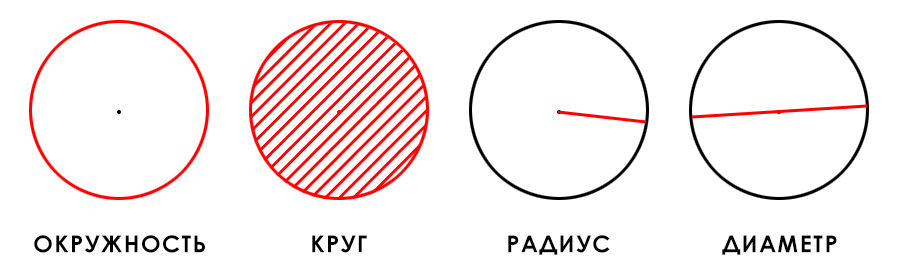
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
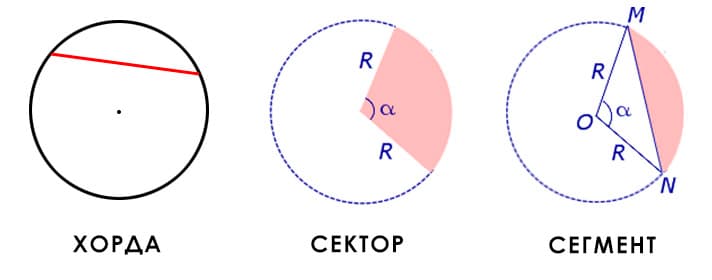
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Содержание
- Какую формулу можно применить для расчета размера жилой зоны в частном доме
- С чего начинать
- В каком классе изучают площадь прямоугольника?
- Обозначение площади
- Треугольник
- 1. Если известна сторона и высота.
- 2. Если известны две стороны и синус угла.
- 3. Если есть радиус описанной окружности.
- Прямоугольник
- Квадрат
- Трапеция
Если помещение обычное и не имеет выступающих частей, вычислить площадь помещения несложно. Измерьте длину и ширину и отметьте их на листе бумаги. Напишите данные измерений с десятичной запятой в сантиметрах.
Например, длина составляет 4,35 метра (430 см), а ширина — 3,25 метра (325 см). Как рассчитать площадь комнаты. Перемножьте полученные числа, чтобы получить площадь комнаты в квадратных метрах.
Возвращаясь к нашему примеру, мы имеем: 4. 35 м * 3. 25 м = 14, 1375 кв.
м. Это значение обычно округляется, так как после запятой остается две цифры.
Отвечает Климова Г. 09. 03. 22.
Какую формулу можно применить для расчета размера жилой зоны в частном доме
Чтобы определить площади, имеющиеся в вашем доме, нужны размеры всех помещений, предназначенных для жилья.
Чтобы знать, какие площади дома следует считать пригодными для жилья, можно тщательно пересмотреть и изучить проект дома и его технический паспорт. Размеры площадей и категории каждого помещения приведены в подробном перечне
Жилая комната: гостиная.
- Главная спальня.
- Гардеробная.
- Чтобы правильно измерить жилую комнату, необходимо тщательно измерить длину и ширину всех существующих стен в каждой комнате, предназначенной для постоянного использования. Это можно сделать с помощью строительного метра. Рекомендуется проводить измерения точно и аккуратно. Перед проведением измерений следует убрать из комнаты все лишние предметы, а измерять удобнее вдоль кирпичей пола, отведя место у каждой стены. Все проведенные замеры следует записать, а также зафиксировать помещение, в котором они были произведены.
После того как проведены замеры жилого помещения и все точно записано, можно приступать к расчету необходимых величин. Для точных расчетов можно применять следующие типы
e (длина) комнаты x w (ширина) = p (площадь) комнаты.
Результаты полученных измерений следует записывать и комментировать. Это облегчит выполнение большего объема работы в домашних условиях в будущем. Далее сложите все измерения, которые вы сделали для каждой комнаты. Это даст вам представление о жилой площади вашей недвижимости.
Самое время вспомнить школьную математику — для вычисления площади вам понадобятся три вещи
С чего начинать
Длина — обычно 4 или 4,5 метра.
- Ширина — стандартное значение для большинства домов составляет 3 или 3,5 метра.
- Высота — в новых зданиях она обычно составляет 2,5 метра. Однако в сталинских зданиях этот показатель может достигать 3 метров.
- Решая задачу по вычислению площади, не делайте этого без соответствующих инструментов.
Рулетка, рулетка
- Угол строения,
- карандаш
- Компьютер,.
- Нивелир.
- Если вы планируете много писать, предпочтительнее использовать блокнот или тетрадь вместо бумаги. Листки имеют тенденцию теряться, и не всегда их можно найти позже, когда они необходимы. Ленты нуждаются в приспособлении для фиксации. В противном случае возникают сложности, и расчеты могут превратиться в настоящую пытку.
Математика 3 класс Урок 22 — Площадь прямоугольника. Вы узнаете: как вычислить площадь прямоугольника. Вы узнаете: как сравнивать геометрические фигуры по площади.
Вычислите площадь прямоугольника. Площадь — это внутренняя часть геометрической фигуры. Площадь измеряется в квадратных сантиметрах.
Чтобы найти площадь прямоугольника, его длину нужно умножить на ширину. Интересные факты о геометрических фигурах Первые упоминания о геометрических фигурах встречаются у древних египтян и древних шумеров.
В каком классе изучают площадь прямоугольника?
В геометрии фигура определяется как плоскость, отрезок плоскости или набор точек в пределах криволинейной поверхности, ограниченной со всех сторон. В реальной жизни нас окружают различные объекты, характеризующиеся как фигуры, например, мобильные телефоны, холодильники и летающие змеи. В этой статье описано несколько способов определения местоположения области.
Обозначение площади
Если параметр фигуры задан в разных единицах длины, решить задачу невозможно. Поэтому для правильного решения задачи все данные должны быть переведены в одну единицу измерения.
Общие единицы измерения для площади :
Квадратные миллиметры (мм 2 ),
- квадратный сантиметр (см 2 ),.
- квадратный десятичный метр (дм 2 ), квадратный метр (м2 ), квадратный метр (м2 ), квадратный метр (м2 ).
- квадратный метр (м 2 ), квадратный километр (км 2 )
- квадратный километр (км 2 ), гектар (га)
- гектар (га).
- Советы, статьи, видео и контрольные списки по обучению доставляются в ваш почтовый ящик
Круг — это множество точек на плоскости, равноудаленных от центра и заключенных в окружность. Радиусом обычно называют отрезок прямой, соединяющий центр окружности с любой точкой.
S = π × r 2 , где r — радиус, а π — константа, равная отношению окружности круга к его диаметру, которое всегда равно 3. 14.
S = & amp; pi × d 2 : 4, где d — диаметр.
S = L 2 : (4 × pi), где L — длина окружности.
Нужно быстро подтянуть знания перед экзаменом? Запишитесь на курс ЕГЭ по математике от Skysmart!
Треугольник — это геометрическая фигура, которая не лежит на прямой линии, а состоит из трех точек, соединенных тремя отрезками прямых. Эти три точки называются вершинами, а отрезки прямых — ребрами. Площадь треугольника может быть вычислена из исходных данных несколькими способами. Давайте рассмотрим их.
Треугольник
S = 0. 5 × a × h, где a — длина основания, а h — высота до основания.
1. Если известна сторона и высота.
Основания могут располагаться в различных положениях, например
Для тупых углов высота отражается на продолжении основания.
В случае прямого угла основание и высота являются его катетами: s
s = 0. 5 x α x β * sina, где a и b — две стороны, а sina — полутонна между ними.
2. Если известны две стороны и синус угла.
s = (a x b x c) : (4 x r), где a, b и c — стороны треугольника, а r — радиус контура.
3. Если есть радиус описанной окружности.
s = p×r, где p — половина лимперметра треугольника, а r — радиус записанного контура.
Прямоугольник
s = a × b, где a и b — длина и ширина прямоугольника.
s = a x √ (d 2-a 2), где a — известная сторона, а d — диагональ.
Диагональ — это отрезок, соединяющий противоположные углы. Она присутствует во всех геометриях, где число вершин превышает 3.
s = 0. 5 x d 2 x ( ), где d — диагональ, а a — угол между диагоналями.
Квадрат — это то же самое, что и прямоугольник, но все стороны могут быть равны. Найти его площадь просто: s
Квадрат
s = a 2, где a — сторона квадрата.
s = d 2:2, где d — диагональ.
Таблица представляет собой четырехугольник с двумя параллельными и двумя непараллельными сторонами.
Трапеция
S = 0. 5 x (A + B) x H, где A и B — два разных основания, а H — высота трапеции.
Высоту трапеции можно построить, проведя отрезки, соединяющие параллельные стороны под прямым углом.
Прямоугольник — это четырехугольник, противоположные стороны которого параллельно-параллельны.
Площадь круга через Диаметр
S – площадь круга,
d – диаметр круга,
π ≈ 3,141592653589
Площадь круга через Радиус
S – площадь круга,
r – радиус круга,
π ≈ 3,141592653589
Площадь круга через Длину Окружности
S – площадь круга,
l – длина окружности,
π ≈ 3,141592653589
Определения и термины
Круг – множество точек плоскости, расстояние до которых от данной точки (центра круга) не превышает заданного расстояния (радиуса круга).
Радиус круга – отрезок, соединяющий центр круга с любой точкой, которая лежит на внешней окружности круг
Диаметр круга – отрезок, соединяющий любые две точки, лежащие на внешней окружности круга, и проходящий через центр круга
Окружность – замкнутая плоская кривая состоящия из всех точек полскости равноудаленных от заданной точки (центра окружности)
Число Пи (π) – математическая константа, которая выражает отношение длины окружности к её диаметру.
Равно приблизительно 3,141592653589…
Площадь окружности
Окружность, по своей сути, является границей круга – замкнутой плоской кривой. Из определения следует, что площади окружности не существует,
а существует Площадь круга.
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади цилиндра
- 1. Боковая поверхность
-
2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h

Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
Площадь круга. Онлайн-калькулятор
Онлайн калькулятор для расчета площади круга. Рассчитать площадь круга можно двумя способами: через радиус и диаметр круга. После выбора вариант расчета, задайте радиус или диаметр и нажмите кнопку “Рассчитать”. Наш калькулятор выведет результат расчета площади, а также покажет подробное решение, с помощью которого можно посмотреть как был получен результат.

Выберите способ расчета площади:
Рассчитать
Круг – это плоскость, которая ограничена окружностью.
Как найти площадь круга?
Площадь круга рассчитывается двумя способами:
1) через радиус круга
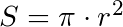
r – радиус круга.
2) через диаметр круга

d – диаметр круга.
