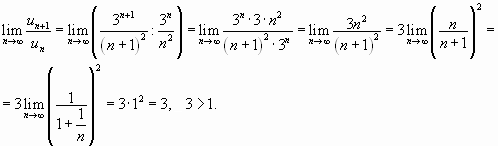Как найти суммарную сумму

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} – frac{1}{2} frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$

$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$

$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$

$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$

$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$

Выносим дробь одну вторую $ frac{1}{2} $ за скобки:

$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$

$$ + … frac{1}{2n-1} – frac{1}{2n+1} + frac{1}{2n+1} – frac{1}{2n+3} bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$

$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$

MS Excel – табличный процессор, способный обрабатывать и систематизировать большие объемы информации, проводить расчеты посредством встроенного инструментария и ввода формул. У пользователя может возникнуть вопрос: «Как в Экселе посчитать сумму и применить формулы?». Чтобы не производить расчеты  чисел вручную, опытные пользователи пользуются несколькими вариантами.

Функция «Автосуммирование»

В вопросе: «Как посчитать сумму в Excel в столбце или строке?» MS Excel предлагает задействуют встроенный инструментарий. Для этого юзеру необходимо:

• создать таблицу с числовой информацией (или использовать имеющуюся).
• разместить в столбце числа, требующие подсчета;
• выделить диапазон ячеек с введенной информацией;
• найти на панели инструментов и активировать пиктограмму со значком суммы ∑.

Результат – автоматический подсчет числовых данных и вывод суммы в следующей строке.

Пиктограмма автосуммирования предлагает второй вариант, когда результат выводится в отдельной ячейке. Для этого пользователь:

• выбирает ячейку, находящуюся в том же столбце что и числа, но несколько ниже;
• кликает на пиктограмму суммы на панели инструментов;
• MS Excel предлагает подсчитать все, что располагается выше обозначенной ячейки, но диапазон захватывает и пустые ячейки;
• изменяет диапазон через выделение мышкой или ручной ввод диапазона;
• для вступления изменений в силу нажимает «Enter».

Строка состояния

Пользователей заинтересует способ, как в Excel посчитать сумму столбца, без фактического математического расчета. Если нет необходимости в фиксации результата суммы и нужно узнать, как считать в Экселе без применения формул, то пользователь:

• вводит числовую информацию в столбце;
• выделяет диапазон.

MS Excel показывает результат суммирования в строке состояния в нижней части окна приложения. Здесь отображается среднее арифметическое и количество элементов в диапазоне.

Примечание: при таком способе результат суммирования нигде не фиксируется.

Использование функций

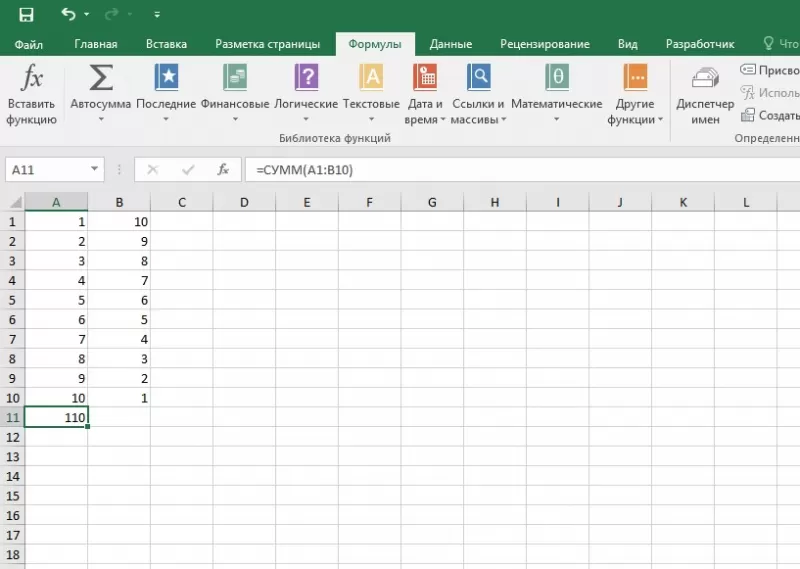
Табличный процессор обладает мощным функционалом, поэтому пользователей интересует опрос, как считать в Excel. Приложение предлагает воспользоваться формулами. Распространенная формула: «=СУММ» – находит сумму введенных чисел.

Для нахождения результата пользователь:

• выбирает ячейку отображения результата;
• устанавливает курсор в строке формул;
• вводит функцию =сумм(диапазон ячеек);
• Нажимает «Enter».

Примечание: когда пользователь начинает вводить формулу, приложение выводит плавающую подсказку-справку. Здесь отображается, как должна выглядеть функция, какие должны быть аргументы. В конкретной функции в круглых скобках указывается диапазон подсчитываемых ячеек. Он либо вводится вручную, либо выделяется мышкой.

Суммирование

Суммирование – важная операция, необходимая для подсчета данных в различных сферах. Если с нахождением суммы диапазона не возникает вопросов, как посчитать сумму ячеек в Excel, если даны одно или несколько условий.

Сумма с одним условием

Дана задача, при которой нужно подсчитать сумму ячеек при выполнении конкретного условия. Здесь пользователь применяет функцию, аналогичную фильтру значений. Проверка выполняется в:

• текстовом;
• численном формате.

Текстовое значение

Для решения задачи с одним условием в виде текстового значения юзер:

• создает таблицу;
• выбирает ячейку, где будет подсчитана сумма, и устанавливает курсор в строку формул;
• вводит команду: =суммесли (условия выполнения).
• последовательно указывает диапазон значений, условие отбора, диапазон суммирования.
• для получения результата нажимает «Enter». В выбранной ячейке указывает сумму тех значений, которые удовлетворяют поставленному условию.

Примечание: Первый параметр – диапазон значений, среди которых будет проводиться отбор.

Второй параметр – критерий, указывающий, что нужно искать.

Третий параметр – диапазон суммирования, из которого будут выбираться значения, удовлетворяющие второму параметру, и складываться.

Критерий отбора указывается в кавычках.

Между параметрами функции обязательно должен быть разделитель «;» (точка с запятой). В противном случае приложение выдаст ошибку о неверно написанной функции.

После введения формулы нужно обязательно проверить правильность расстановки скобок.

Численное значение

Для получения суммы с одним условием в численном формате пользователь:

• формирует таблицу;
• выбирает ячейку, где будет отображаться итог решения задачи;
• переходит в строку формул;
• вписывает функцию: =суммесли (условия выполнения);
• действует согласно предыдущему алгоритму, указывая условия отбора и диапазоны значений;
• для получения результата нажимает «Enter». В выбранной ячейке указывается сумма тех значений, которые удовлетворяют поставленному условию.

Сумма с несколькими условиями

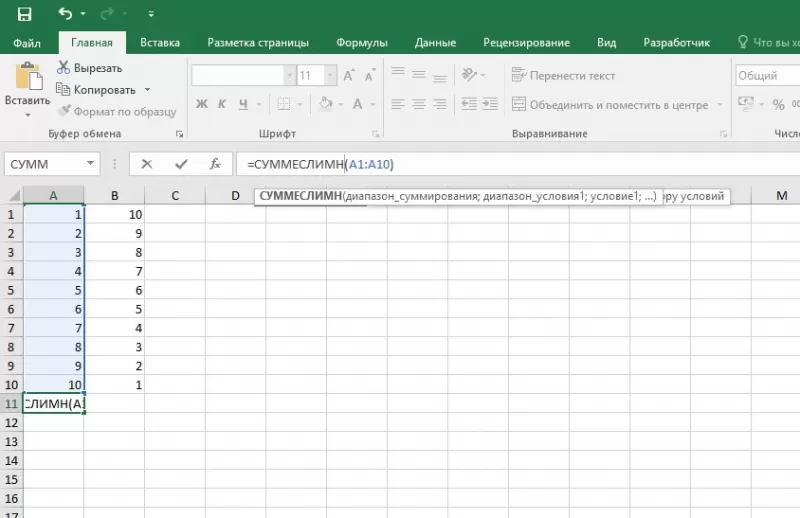
Иногда юзеру нужно решить задачу, где указаны 2 и более условий, и нужно найти сумму значений, удовлетворяющих заданным критериям. Для этого используется функция «=СУММЕСЛИМН». Поэтому важно знать, как в Экселе сделать сумму с несколькими условиями. Для этого пользователь:

• формирует таблицу по заданному образцу;
• выбирает ячейку, где будет отображаться итог решения задачи;
• переходит в строку формул;
• вписывает функцию: =суммеслимн (условия выполнения).
• последовательно указывает диапазон сложения, диапазон условия1, условие1 и т.д.;
• для получения результата нажимает «Enter». В выбранной ячейке указывает сумма тех значений, которые удовлетворяют поставленному условию.

Примечание: Первый параметр – диапазон сложения, из которого будут выбираться значения, удовлетворяющие условиям, и складываться.

Второй параметр – диапазон условия 1, указывающий столбец, в котором проходит фильтрация по первому условию.

Третий параметр – условие1, которое указывается в кавычках и задает фильтрацию.

Четвертый и последующий параметры аналогичны второму и третьему, т.е. диапазон условия2, условие2; диапазон условия3, условие3 и т.д.

Условий отбора может множество.

Между параметрами функции обязательно должен быть разделитель «;» (точка с запятой). В противном случае приложение выдаст ошибку о неверно написанной функции.

После введения формулы нужно обязательно проверить правильность расстановки скобок.

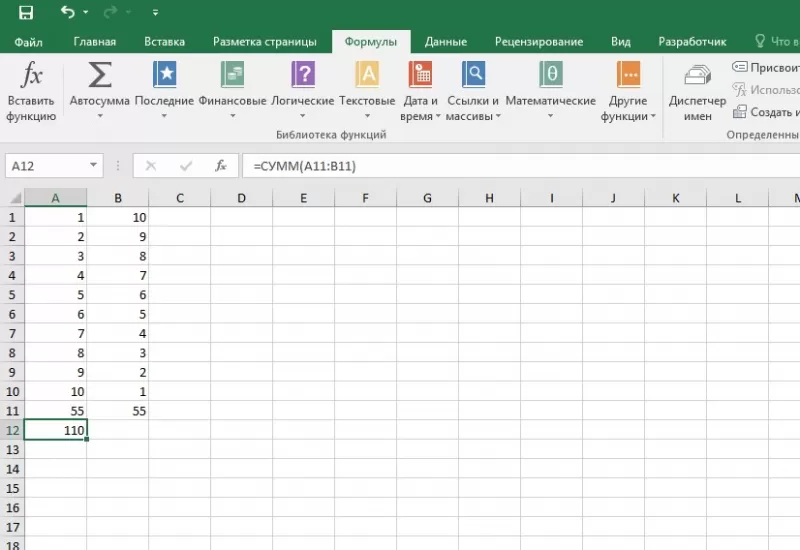
Произведение двух столбцов

Возникают ситуации, когда нужно знать, как посчитать сумму в Excel через произведение двух столбцов. Для этого пользователь:

• вводит значения в 2 столбца;
• выбирает ячейку, где отображается результат;
• устанавливает курсор в строку формул и вводит текст:=сумм (диапазон ячеек одного столбца ) *сумм(диапазон ячеек другого столбца);
• для получения результата нажимает «Enter».

Примечание: при ручном написании функций важно проверить правильность расстановки скобок. В противном случае приложение выдаст сообщение об ошибке и предложит исправить недочет.

II способ

Для получения произведения двух столбцов пользователь:

• находит сумму чисел в первом и втором столбце;
• в произвольной ячейке отмечает произведение двух сумм путем написания формулы в строке формулы или непосредственно в ячейке;
• нажимает «Enter».

Ручной ввод формулы

Следующий вариант – как посчитать общую сумму в Excel посредством ручного ввода функции. Для решения задачи по заданному методу пользователь:

• устанавливает курсор в выбранной ячейке (дважды щелкнуть по ячейке);
• прописывает формулу, начиная со знака «=»;
• мышкой кликает по тем ячейкам, которые нужно поочередно сложить;
• после окончания формулы нажимает «Enter».

Нахождение суммы числового ряда. Первая часть.

В теме про основные понятия числовых рядов было указано определение суммы ряда. Вот оно:

Если существует конечный предел $S=lim_{ntoinfty}S_n$, то его называют суммой ряда $sumlimits_{n=1}^{infty}u_n$ и сам ряд именуют сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд называют расходящимся.

Если понятие “частичная сумма” вызывает вопросы, то советую посмотреть раздел про частичную сумму ряда, обратив внимание на пример №4. В этом примере подробно раскрывается суть частичной суммы и остатка.

В данной теме нас будет интересовать вопрос нахождения сумм числовых рядов по определению. Определение суммы ряда опирается на значение $lim_{ntoinfty}S_n$, поэтому для нахождения суммы нам нужно выполнить два шага:

1. Составить n-ю частичную сумму $S_n$;
2. Найти $lim_{ntoinfty}S_n$ (если он существует).

Если конечный $lim_{ntoinfty}S_n$ существует, то его значение и будет суммой рассматриваемого ряда, а сам ряд будет именоваться сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд будет расходиться. Есть несколько стандартных приёмов, которые применяются для нахождения суммы числовых рядов. Например, для нахождения суммы ряда, общий член которого имеет вид рациональной дроби $u_n=frac{P(n)}{Q(n)}$, вполне подходит такой алгоритм:

1. Разложить дробь $frac{P(n)}{Q(n)}$ на элементарные дроби (процедура разложения описана тут).
2. Записать выражение для частичной суммы $S_n$, используя результаты предыдущего пункта.
3. Перегруппировать слагаемые в выражении для $S_n$, приведя их к удобному для сокращения виду.
4. Используя результат предыдущего пункта, найти $lim_{ntoinfty}S_n$.

Для нахождения суммы ряда нередко удобно использовать и такое свойство:

Пусть общий член ряда $sumlimits_{n=1}^{infty}u_n$ можно представить в виде $u_n=b_{n+1}-b_n$. Если существует конечный предел $lim_{ntoinfty}b_n=b$, то ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом частичная сумма ряда равна $S_{n}=b_{n+1}-b_1$, а сумма ряда $S=b-b_1$.

Доказательство этого свойства может быть интересно не всем читателям, поэтому я скрою его под примечание.

Доказательство свойства: показатьскрыть

Во всех изложенных ниже примерах члены рядов будем обозначать буквами $u_1$ (первый член ряда), $u_2$ (второй член ряда) и так далее. Запись $u_n$ будет обозначать общий член ряда.

Пример №1

Найти сумму ряда $sumlimits_{n=1}^{infty}(-1)^{n+1}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=(-1)^{n+1}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=\=(-1)^2+(-1)^3+(-1)^4+(-1)^5+ldots+(-1)^{n+1}=1-1+1-1+ldots+(-1)^n.
$$

Вопрос в следующем: чему равна эта сумма? Если в частичных суммах мы станем брать чётное количество слагаемых, они попарно сократятся:

begin{aligned}
& S_2=1-1=0;\
& S_4=1-1+1-1=0;\
& S_6=1-1+1-1+1-1=0;\
& S_8=1-1+1-1+1-1+1-1=0.
end{aligned}

Итак, частичная сумма, содержащая чётное количество слагаемых, равна 0. Т.е. если $n$ – чётное число, то $S_n=0$. Фразу “n – чётное число” можно записать так: $n=2k$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1=2$, $n=2cdot 2=4$, $n=2cdot 3=6$, $n=2cdot 4=8$ и так далее. Итак, $S_{2k}=0$.

Если мы станем брать нечётное количество слагаемых (1, 3, 5 и т.д.), то сумма станет равна 1:

begin{aligned}
& S_1=1;\
& S_3=1-1+1=1;\
& S_5=1-1+1-1+1=1;\
& S_7=1-1+1-1+1-1+1=1.
end{aligned}

Таким образом, если $n$ – нечётное число, то $S_n=1$. Фразу “n – нечётное число” можно записать так: $n=2k-1$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1-1=1$, $n=2cdot 2-1=3$, $n=2cdot 3-1=5$, $n=2cdot 4-1=7$ и так далее. Итак, $S_{2k-1}=1$.

Формально равенство $S_{2k-1}=1$ можно доказать с помощью формулы $S_{2k}=S_{2k-1}+u_{2k}$. Так как $S_{2k}=0$, то $S_{2k-1}+u_{2k}=0$, т.е. $S_{2k-1}=-u_{2k}$. Так как $u_{2k}=(-1)^{2k+1}=left((-1)^2right)^kcdot (-1)^1=-1$, то $S_{2k-1}=-(-1)=1$.

Возникает вопрос: как быть с пределом $lim_{ntoinfty}S_n$? Ведь если $n$ – чётное число, т.е. $n=2k$, то:

$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k}=lim_{ktoinfty}0=0.
$$

С другой стороны, если $n$ – нечётное число, то:

$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k-1}=lim_{ktoinfty}1=1.
$$

Что мы получили? А получили мы следующее: последовательность частичных сумм ${S_n}$ имеет две подпоследовательности: ${S_{2k-1}}$ и ${S_{2k}}$, пределы которых различны. Следовательно, последовательность ${S_n}$ не имеет предела. Вывод: ряд не имеет суммы, т.е. расходится.

Здесь стоит обратить внимание вот на что: следует различать случаи, когда предел равен бесконечности (см. следующий пример №2), и когда предела попросту не существует. Хотя и в том и в другом случаях ряд будет расходиться.

Ответ: ряд расходится.

Пример №2

Найти сумму ряда $sumlimits_{n=1}^{infty}(3n+1)$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=3n+1$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=4+7+10+13+ldots+3n+1.
$$

Эту сумму можно записать в более коротком виде. Дело в том, что последовательность 4, 7, 10, 13 и т.д. есть арифметическая прогрессия, первый член которой равен 4, а разность равна 3. Сумма первых n членов этой прогрессии такова:

$$
4+7+10+13+ldots+3n+1=frac{4+3n+1}{2}cdot n=frac{3n+5}{2}cdot{n}.
$$

Итак, $S_n=frac{3n+5}{2}cdot n$. Найдем $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{3n+5}{2}cdot nright)=+infty.
$$

Так как $lim_{ntoinfty}S_n=+infty$, то ряд расходится.

Если немного выйти за рамки данной темы, то стоит отметить, что расходимость этого ряда легко доказывается с помощью необходимого признака сходимости.

Ответ: ряд расходится.

Пример №3

Найти сумму ряда $sumlimits_{n=1}^{infty}frac{2}{(2n+1)(2n+3)}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{2}{(2n+1)(2n+3)}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}.
$$

Почему я пишу именно $frac{2}{3cdot 5}$, а не $frac{2}{15}$, будет ясно из дальнейшего повествования. Однако запись частичной суммы ни на йоту не приблизила нас к цели. Нам ведь нужно найти $lim_{ntoinfty}S_n$, но если мы просто запишем:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}right),
$$

то эта запись, совершенно верная по форме, ничего нам не даст по сути. Чтобы найти предел, выражение частичной суммы предварительно нужно упростить.

Для этого есть стандартное преобразование, состоящее в разложении дроби $frac{2}{(2n+1)(2n+3)}$, которая представляет общий член ряда, на элементарные дроби. Вопросу разложения рациональных дробей на элементарные посвящена отдельная тема (см., например, пример №3 на этой странице). Раскладывая дробь $frac{2}{(2n+1)(2n+3)}$ на элементарные дроби, будем иметь:

$$
frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}=frac{Acdot(2n+3)+Bcdot(2n+1)}{(2n+1)(2n+3)}.
$$

Приравниваем числители дробей в левой и правой частях полученного равенства:

$$
2=Acdot(2n+3)+Bcdot(2n+1).
$$

Чтобы найти значения $A$ и $B$ есть два пути. Можно раскрыть скобки и перегруппировать слагаемые, а можно просто подставить вместо $n$ некие подходящие значения. Сугубо для разнообразия в этом примере пойдём первым путём, а следующем – будем подставлять частные значения $n$. Раскрывая скобки и перегруппировывая слагаемые, получим:

$$
2=2An+3A+2Bn+B;\
2=(2A+2B)n+3A+B.
$$

В левой части равенства перед $n$ стоит ноль. Если угодно, левую часть равенства для наглядности можно представить как $0cdot n+ 2$. Так как в левой части равенства перед $n$ стоит ноль, а в правой части равества перед $n$ стоит $2A+2B$, то имеем первое уравнение: $2A+2B=0$. Сразу разделим обе части этого уравнения на 2, получив после этого $A+B=0$.

Так как в левой части равенства свободный член равен 2, а в правой части равенства свободный член равен $3A+B$, то $3A+B=2$. Итак, имеем систему:

$$
left{begin{aligned}
& A+B=0;\
& 3A+B=2.
end{aligned}right.
$$

Можно решать эту систему методом Крамера, методом Гаусса или с помощью обратной матрицы. Однако проще всего банально выразить из первого уравнения $A=-B$ и подставить во второе:

$$
3cdot (-B)+B=2;; -2B=2; ; B=-1.
$$

Так как $B=-1$, то $A=-B=1$. Подставляя найденные значения $A=1$ и $B=-1$ в формулу $frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}$, будем иметь:

$$
frac{2}{(2n+1)(2n+3)}=frac{1}{2n+1}+frac{-1}{2n+3}=frac{1}{2n+1}-frac{1}{2n+3}.
$$

Итак, $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Используем полученное разложение для того, чтобы упростить формулу частичной суммы ряда. Покажу сначала решение стандартным путём, принятым в большинстве решебников и методичек.

Первый способ упрощения формулы для частичной суммы.

Мы получили разложение общего члена ряда на две дроби: $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Чтобы этот результат был более наглядным, я распишу несколько первых членов ряда по этой формуле:

begin{aligned}
& u_1=frac{2}{3cdot 5}=frac{1}{3}-frac{1}{5};\
& u_2=frac{2}{5cdot 7}=frac{1}{5}-frac{1}{7};\
& u_3=frac{2}{7cdot 9}=frac{1}{7}-frac{1}{9};\
& u_4=frac{2}{9cdot 11}=frac{1}{9}-frac{1}{11}.
end{aligned}

Давайте распишем частичную сумму, учитывая полученное разложение каждого элемента:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}.
$$

Как видите, все слагаемые этой суммы сокращаются, – кроме первого и последнего:

Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Этот способ упрощения формулы для частичной суммы имеет простую суть: разложить общий член ряда на элементарные дроби, а потом сократить слагаемые.

Однако можно ли считать вышеуказанные рассуждения строгим доказательством? Полагаю, что в общем случае нет, и поясню почему. Дело в том, что мы должны “увидеть” (как любят писать некоторые авторы – “легко увидеть”), что слагаемые сокращаются. А если мы “увидим” не все слагаемые, которые останутся после сокращения? Где гарантии, что мы сократим именно то, что нужно? Нет гарантий. Понятно, что в случае рассматриваемой конкретной задачи всё тривиально и очевидно, но далеко не все частичные суммы рядов имеют такую простую структуру.

Формулу $S_n=frac{1}{3}-frac{1}{2n+3}$ можно принять в качестве гипотезы, которую ещё нужно доказать. Доказательство удобнее всего проводить методом математической индукции. Так как доказательством заинтересуются не все читатели, то я его скрыл под примечание.

Доказательство формулы $S_n=frac{1}{3}-frac{1}{2n+3}$: показатьскрыть

В стандартном курсе высшей математики обычно довольствуются “вычёркиванием” сокращающихся слагаемых, не требуя никаких доказательств. Итак, мы получили выражение для n-й частичной суммы: $S_n=frac{1}{3}-frac{1}{2n+3}$. Найдём значение $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$

Вывод: заданный ряд сходится и сумма его $S=frac{1}{3}$.

Второй способ упрощения формулы для частичной суммы.

Этот способ основан на свойстве, записанном в начале страницы. По сути, он схож с предыдущим, – разница лишь в применении уже готовой теоремы, доказанной нами ранее. Вернёмся к записи общего члена ряда:

$$
u_n=frac{1}{2n+1}-frac{1}{2n+3}
=frac{-1}{2n+3}-frac{-1}{2n+1}
$$

Обозначим $b_n=frac{-1}{2n+1}$, тогда $b_{n+1}=frac{-1}{2(n+1)+1}=frac{-1}{2n+3}$. Таким образом, $u_{n}=b_{n+1}-b_{n}$. При этом $lim_{ntoinfty}b_n=0$. Согласно упомянутому свойству, ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом его сумма равна $S=0-b_1=frac{1}{3}$. Если есть необходимость, можно записать и частичную сумму ряда:

$$
S_n
=b_{n+1}-b_1
=frac{-1}{2n+3}-left(-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Третий способ упрощения формулы для частичной суммы.

Честно говоря, я сам предпочитаю большей частью именно этот способ 🙂 Давайте запишем частичную сумму в сокращённом варианте:

$$
S_n=sumlimits_{k=1}^{n}u_k=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}.
$$

Мы получили ранее, что $u_k=frac{1}{2k+1}-frac{1}{2k+3}$, поэтому:

$$
S_n=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right).
$$

Сумма $S_n$ содержит конечное количество слагаемых, поэтому мы можем переставлять их так, как нам заблагорассудится. Я хочу сначала сложить все слагаемые вида $frac{1}{2k+1}$, а уж затем переходить к слагаемым вида $frac{1}{2k+3}$. Это означает, что частичную сумму мы представим в таком виде:

$$
S_n
=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}=\
=frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+1}-left(frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+3}right).
$$

Конечно, развёрнутая запись крайне неудобна, поэтому представленное выше равенство оформим более компактно:

$$
S_n=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}.
$$

Теперь преобразуем выражения $frac{1}{2k+1}$ и $frac{1}{2k+3}$ к одному виду. Приведём, например, дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Выражение в знаменателе дроби $frac{1}{2k+3}$ я представлю в таком виде:

$$
frac{1}{2k+3}=frac{1}{2k+2+1}=frac{1}{2(k+1)+1}.
$$

И сумму $sumlimits_{k=1}^{n}frac{1}{2k+3}$ теперь можно записать так:

$$
sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$

Если равенство $sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ не вызывает вопросов, то пойдём далее. Если же вопросы есть, то прошу развернуть примечание.

Как мы получили преобразованную сумму? показатьскрыть

Таким образом, частичную сумму можно представить в следующем виде:

$$
S_n=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$

Заметьте, что суммы $sumlimits_{k=1}^{n}frac{1}{2k+1}$ и $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ отличаются лишь пределами суммирования. Сделаем эти пределы одинаковыми. Начнём с первой суммы.

Сделаем так, чтобы верхний предел суммирования стал равен $n+1$. Если $k=n+1$, то $frac{1}{2k+1}=frac{1}{2n+3}$. Прибавляя и вычитая из первой суммы $frac{1}{2n+3}$, получим:

$$
sumlimits_{k=1}^{n}frac{1}{2k+1}
=sumlimits_{k=1}^{n}frac{1}{2k+1}+frac{1}{2n+3}-frac{1}{2n+3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}
$$

Для второй суммы $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ сделаем так, чтобы нижний предел суммирования был равен 1. Если $k=1$, то $frac{1}{2k+1}=frac{1}{3}$. Прибавляя и вычитая $frac{1}{3}$, получим:

$$
sumlimits_{k=2}^{n+1}frac{1}{2k+1}
=sumlimits_{k=2}^{n+1}frac{1}{2k+1}+frac{1}{3}-frac{1}{3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}
$$

С учётом полученных результатов, выражение для $S_n$ примет такой вид:

$$
S_n
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Если пропустить все пояснения, то процесс нахождения сокращённой формулы для n-й частичной суммы примет такой вид:

$$
S_n=sumlimits_{k=1}^{n}u_k
=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}
=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=\

=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}
=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}=\

=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Напомню, что мы приводили дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Разумеется, можно поступить и наоборот, т.е. представить дробь $frac{1}{2k+1}$ в виде $frac{1}{2k+3}$. Конечное выражение для частичной суммы не изменится. Процесс нахождения частичной суммы в этом случае я скрою под примечание.

Как найти $S_n$, если приводить к виду иной дроби? показатьскрыть

Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Находим предел $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$

Заданный ряд сходится и сумма его $S=frac{1}{3}$.

Ответ: $S=frac{1}{3}$.

Продолжение темы нахождения суммы ряда будет рассмотрено во второй и третьей частях.

time_interval = [4, 6, 12]

Я хочу подвести цифры, такие как [4, 4+6, 4+6+12], чтобы получить список t = [4, 10, 22].

Я попробовал следующее:

for i in time_interval:
    t1 = time_interval[0]
    t2 = time_interval[1] + t1
    t3 = time_interval[2] + t2
    print(t1, t2, t3)

4 10 22
4 10 22
4 10 22

Ответ 1

Если вы делаете много численную работу с такими массивами, я предлагаю numpy, который поставляется с функцией суммарной суммы cumsum:

import numpy as np

a = [4,6,12]

np.cumsum(a)
#array([4, 10, 22])

Ненусы часто быстрее, чем чистый питон для такого рода вещей, см. в @Ashwini accumu:

In [136]: timeit list(accumu(range(1000)))
10000 loops, best of 3: 161 us per loop

In [137]: timeit list(accumu(xrange(1000)))
10000 loops, best of 3: 147 us per loop

In [138]: timeit np.cumsum(np.arange(1000))
100000 loops, best of 3: 10.1 us per loop

Но, конечно, если это единственное место, которое вы будете использовать numpy, возможно, не стоит зависеть от него.

Ответ 2

В Python 2 вы можете определить свою собственную функцию генератора следующим образом:

def accumu(lis):
    total = 0
    for x in lis:
        total += x
        yield total

In [4]: list(accumu([4,6,12]))
Out[4]: [4, 10, 22]

И в Python 3.2+ вы можете использовать itertools.accumulate():

In [1]: lis = [4,6,12]

In [2]: from itertools import accumulate

In [3]: list(accumulate(lis))
Out[3]: [4, 10, 22]

Ответ 3

Вот:

a = [4, 6, 12]
reduce(lambda c, x: c + [c[-1] + x], a, [0])[1:]

Выведет (как ожидалось):

[4, 10, 22]

Ответ 4

Я сделал оценку двух верхних ответов с Python 3.4, и я обнаружил, что itertools.accumulate быстрее, чем numpy.cumsum при многих обстоятельствах, часто намного быстрее. Однако, как вы можете видеть из комментариев, это может быть не всегда так, и трудно исчерпывающе изучить все варианты. (Не стесняйтесь добавлять комментарий или редактировать этот пост, если у вас есть дополнительные результаты для сравнения.)

Некоторые тайминги…

Для коротких списков accumulate примерно в 4 раза быстрее:

from timeit import timeit

def sum1(l):
    from itertools import accumulate
    return list(accumulate(l))

def sum2(l):
    from numpy import cumsum
    return list(cumsum(l))

l = [1, 2, 3, 4, 5]

timeit(lambda: sum1(l), number=100000)
# 0.4243644131347537
timeit(lambda: sum2(l), number=100000)
# 1.7077815784141421

Для более длинных списков accumulate примерно в 3 раза быстрее:

l = [1, 2, 3, 4, 5]*1000
timeit(lambda: sum1(l), number=100000)
# 19.174508565105498
timeit(lambda: sum2(l), number=100000)
# 61.871223849244416

Если numpy array не отбрасывается до list, accumulate все еще примерно в 2 раза быстрее:

from timeit import timeit

def sum1(l):
    from itertools import accumulate
    return list(accumulate(l))

def sum2(l):
    from numpy import cumsum
    return cumsum(l)

l = [1, 2, 3, 4, 5]*1000

print(timeit(lambda: sum1(l), number=100000))
# 19.18597290944308
print(timeit(lambda: sum2(l), number=100000))
# 37.759664884768426

Если вы помещаете импорт за пределы двух функций и все еще возвращаете numpy array, accumulate все еще почти в 2 раза быстрее:

from timeit import timeit
from itertools import accumulate
from numpy import cumsum

def sum1(l):
    return list(accumulate(l))

def sum2(l):
    return cumsum(l)

l = [1, 2, 3, 4, 5]*1000

timeit(lambda: sum1(l), number=100000)
# 19.042188624851406
timeit(lambda: sum2(l), number=100000)
# 35.17324400227517

Ответ 5

Сначала вы хотите запустить список подпоследовательностей:

subseqs = (seq[:i] for i in range(1, len(seq)+1))

Затем вы вызываете sum для каждой подпоследовательности:

sums = [sum(subseq) for subseq in subseqs]

(Это не самый эффективный способ сделать это, потому что вы добавляете все префиксы несколько раз. Но это, вероятно, не имеет значения для большинства случаев использования, и это легче понять, если у вас нет думать о текущих итогах.)

Если вы используете Python 3.2 или новее, вы можете использовать itertools.accumulate, чтобы сделать это за вас:

sums = itertools.accumulate(seq)

И если вы используете 3.1 или более раннюю версию, вы можете просто скопировать источник “эквивалент” прямо из документов (кроме изменения next(it) до it.next() для 2.5 и более ранних версий).

Ответ 6

values = [4, 6, 12]
total  = 0
sums   = []

for v in values:
  total = total + v
  sums.append(total)

print 'Values: ', values
print 'Sums:   ', sums

Запуск этого кода дает

Values: [4, 6, 12]
Sums:   [4, 10, 22]

Ответ 7

Если вы хотите использовать pythonic без numpy, работая в 2.7, это будет мой способ сделать это

l = [1,2,3,4]
_d={-1:0}
cumsum=[_d.setdefault(idx, _d[idx-1]+item) for idx,item in enumerate(l)]

теперь попробуйте и протестируйте его против всех других реализаций

import timeit
L=range(10000)

def sum1(l):
    cumsum=[]
    total = 0
    for v in l:
        total += v
        cumsum.append(total)
    return cumsum


def sum2(l):
    import numpy as np
    return list(np.cumsum(l))

def sum3(l):
    return [sum(l[:i+1]) for i in xrange(len(l))]

def sum4(l):
    return reduce(lambda c, x: c + [c[-1] + x], l, [0])[1:]

def this_implementation(l):
    _d={-1:0}
    return [_d.setdefault(idx, _d[idx-1]+item) for idx,item in enumerate(l)]


# sanity check
sum1(L)==sum2(L)==sum3(L)==sum4(L)==this_implementation(L)
>>> True    

# PERFORMANCE TEST
timeit.timeit('sum1(L)','from __main__ import sum1,sum2,sum3,sum4,this_implementation,L', number=100)/100.
>>> 0.001018061637878418

timeit.timeit('sum2(L)','from __main__ import sum1,sum2,sum3,sum4,this_implementation,L', number=100)/100.
>>> 0.000829620361328125

timeit.timeit('sum3(L)','from __main__ import sum1,sum2,sum3,sum4,this_implementation,L', number=100)/100.
>>> 0.4606760001182556 

timeit.timeit('sum4(L)','from __main__ import sum1,sum2,sum3,sum4,this_implementation,L', number=100)/100.
>>> 0.18932826995849608

timeit.timeit('this_implementation(L)','from __main__ import sum1,sum2,sum3,sum4,this_implementation,L', number=100)/100.
>>> 0.002348129749298096

Ответ 8

Выражения присваивания из PEP 572 (ожидаемые для Python 3.8) предлагают еще один способ решить эту проблему:

time_interval = [4, 6, 12]

total_time = 0
cum_time = [total_time := total_time + t for t in time_interval]

Ответ 9

Попробуйте это: функция накопления вместе с оператором add выполняет текущее сложение.

import itertools  
import operator  
result = itertools.accumulate([1,2,3,4,5], operator.add)  
list(result)

Ответ 10

Попробуйте следующее:

result = []
acc = 0
for i in time_interval:
    acc += i
    result.append(acc)

Ответ 11

Вы можете рассчитать список накопленных сумм за линейное время с помощью простого цикла for:

def csum(lst):
    s = lst.copy()
    for i in range(1, len(s)):
        s[i] += s[i-1]
    return s

time_interval = [4, 6, 12]
print(csum(time_interval))  # [4, 10, 22]

Стандартная библиотека itertools.accumulate может быть более быстрой альтернативой (поскольку она реализована в C):

from itertools import accumulate
time_interval = [4, 6, 12]
print(list(accumulate(time_interval)))  # [4, 10, 22]

Ответ 12

In [42]: a = [4, 6, 12]

In [43]: [sum(a[:i+1]) for i in xrange(len(a))]
Out[43]: [4, 10, 22]

Это слабее быстрее, чем метод генератора выше @Ashwini для небольших списков

In [48]: %timeit list(accumu([4,6,12]))
  100000 loops, best of 3: 2.63 us per loop

In [49]: %timeit [sum(a[:i+1]) for i in xrange(len(a))]
  100000 loops, best of 3: 2.46 us per loop

Для больших списков генератор – это путь к уверенности.,

In [50]: a = range(1000)

In [51]: %timeit [sum(a[:i+1]) for i in xrange(len(a))]
  100 loops, best of 3: 6.04 ms per loop

In [52]: %timeit list(accumu(a))
  10000 loops, best of 3: 162 us per loop

Ответ 13

Немного взломанный, но, похоже, работает:

def cumulative_sum(l):
  y = [0]
  def inc(n):
    y[0] += n
    return y[0]
  return [inc(x) for x in l]

Я подумал, что внутренняя функция сможет изменить y, объявленную во внешней лексической области, но это не сработало, поэтому вместо этого мы используем некоторые неприятные хаки с модификацией структуры. Возможно, более изящно использовать генератор.

Ответ 14

Без использования Numpy вы можете прокручивать непосредственно по массиву и накапливать сумму на этом пути. Например:

a=range(10)
i=1
while((i>0) & (i<10)):
    a[i]=a[i-1]+a[i]
    i=i+1
print a

Результаты в:

[0, 1, 3, 6, 10, 15, 21, 28, 36, 45]

Ответ 15

def cummul_sum(list_arguement):
    cumm_sum_lst = []
    cumm_val = 0
    for eachitem in list_arguement:
        cumm_val += eachitem
        cumm_sum_lst.append(cumm_val)
    return cumm_sum_lst

Ответ 16

Чистый python oneliner для суммарной суммы:

cumsum = lambda X: X[:1] + cumsum([X[0]+X[1]] + X[2:]) if X[1:] else X

Это рекурсивная версия, основанная на рекурсивных суммарных суммах. Некоторые объяснения:

1. Первый член X[:1] – это список, содержащий предыдущий элемент и почти такой же, как [X[0]] (который будет жаловаться на пустые списки).
2. Рекурсивный вызов cumsum во втором члене обрабатывает текущий элемент [1] и оставшийся список, длина которого будет уменьшена на единицу.
3. if X[1:] короче, if len(X)>1.

Контрольная работа:

cumsum([4,6,12])
#[4, 10, 22]

cumsum([])
#[]

И имитирует совокупный продукт:

cumprod = lambda X: X[:1] + cumprod([X[0]*X[1]] + X[2:]) if X[1:] else X

Контрольная работа:

cumprod([4,6,12])
#[4, 24, 288]

Ответ 17

l = [1,-1,3]
cum_list = l

def sum_list(input_list):
    index = 1
    for i in input_list[1:]:
        cum_list[index] = i + input_list[index-1]
        index = index + 1 
    return cum_list

print(sum_list(l))

Ответ 18

В Python3, чтобы найти совокупную сумму списка, где i -й элемент
сумма первых элементов i + 1 из исходного списка, вы можете сделать:

a = [4 , 6 , 12]
b = []
for i in range(0,len(a)):
    b.append(sum(a[:i+1]))
print(b)

ИЛИ вы можете использовать понимание списка:

b = [sum(a[:x+1]) for x in range(0,len(a))]

Выход

[4,10,22]

Ответ 19

lst = [4,6,12]

[sum(lst[:i+1]) for i in xrange(len(lst))]

Если вы ищете более эффективное решение (более крупные списки?), генератор может быть хорошим вызовом (или просто использовать numpy, если вы действительно заботитесь о перфомансе).

def gen(lst):
    acu = 0
    for num in lst:
        yield num + acu
        acu += num

print list(gen([4, 6, 12]))

Ответ 20

Это будет стиль Haskell:

def wrand(vtlg):

    def helpf(lalt,lneu): 

        if not lalt==[]:
            return helpf(lalt[1::],[lalt[0]+lneu[0]]+lneu)
        else:
            lneu.reverse()
            return lneu[1:]        

    return helpf(vtlg,[0])

Ответ 21

Отвечая на исходный вопрос, спрашивая, как “суммировать числа в списке”: проверьте встроенную функцию sum(), она, вероятно, делает то, что вы хотите.

ВВЕДЕНИЕ

Методическое пособие предназначено для
преподавателей математики в техникумах, а также
для студентов второго курса, всех
специальностей.

В данной работе излагаются основные понятия
теории рядов. Теоретический материал
соответствует требованиям Государственного
образовательного стандарта среднего
профессионального образования (Министерство
образования Российской Федерации. М., 2002г.).

Изложение теоретического материала по всей
теме сопровождается рассмотрением большого
количества примеров и задач, ведется на
доступном, по-возможности строгом языке. В конце
пособия приведены примеры и задания, которые
студенты могут выполнять в режиме самоконтроля.

Пособие предназначено для студентов заочной и
дневной форм обучения.

Учитывая уровень подготовки учащихся
техникума, а также крайне ограниченное число
часов (12 часов + 4 ф.), отводимое программой для
прохождения высшей математики в техникумах,
строгие выводы, представляющие большие
трудности для усвоения, опущены, ограничиваясь
рассмотрением примеров.

ОСНОВНЫЕ ПОНЯТИЯ

Решение задачи, представленной в
математических терминах, например, в виде
комбинации различных функций, их производных и
интегралов, нужно уметь “довести до числа”,
которое чаще всего и служит окончательным
ответом. Для этого в различных разделах
математики выработаны различные методы.

Раздел математики, позволяющий решить любую
корректно поставленную задачу с достаточной для
практического использования точностью,
называется теорией рядов.

Даже если некоторые тонкие понятия
математического анализа появились вне связи с
теорией рядов, они немедленно применялись к
рядам, которые служили как бы инструментом для
испытания значимости этих понятий. Такое
положение сохраняется и сейчас.

Выражение вида

,

где ;;;…;;… – члены ряда; – n-ый или общий член
ряда, называется бесконечным рядом (рядом).

Если члены ряда :

• числа, то ряд называется числовым;
• числа одного знака, то ряд называется
  знакопостоянным;
• числа разных знаков, то ряд называется
  знакопеременным;
• положительные числа, то ряд называется
  знакоположительным;
• числа, знаки которых строго чередуются, то ряд
  называется знакочередующимся;
• функции, то ряд называется функциональным;
• степени, то ряд
  называется степенным;
• тригонометрические функции, то ряд называется
  тригонометрическим.

I. Числовой ряд

1.1. Основные понятия числового ряда.

Числовым рядом называется сумма вида

, (1.1)

где ,,,…,,…, называемые членами ряда,
образуют бесконечную последовательность; членназывается
общим членом ряда.

Суммы

…………..

,

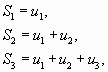
составленные из первых членов ряда (1.1),
называются частичными суммами этого ряда.

Каждому ряду можно сопоставить
последовательность частичных сумм .

Если при бесконечном возрастании номера n
частичная сумма ряда стремится к пределу, то ряд называется сходящимся, а
число –
суммой сходящегося ряда, т.е.

и .

Эта запись равносильна записи

.

Если частичная сумма ряда (1.1) при неограниченном
возрастании n не имеет конечного предела
(стремится к
или ), то
такой ряд называется расходящимся.

Если ряд сходящийся, то значение при достаточно
большом n является приближенным
выражением суммы ряда S.

Разность
называется остатком ряда. Если ряд сходится, то
его остаток стремится к нулю, т.е., и наоборот, если остаток
стремится к нулю, то ряд сходится.

1.2. Примеры числовых рядов.

Пример 1. Ряд вида

(1.2)

называется геометрическим .

Геометрический ряд образован из членов
геометрической прогрессии.

Известно, что сумма её первых n членов . Очевидно: это n-ая
частичная сумма ряда (1.2).

Возможны случаи:

:

.

Ряд (1.2) принимает вид:

,

, ряд
расходится;

Ряд (1.2) принимает вид:

,

не имеет
предела, ряд расходится.

,

– конечное
число, ряд сходится.

,

– ряд
расходится.

Итак, данный ряд сходится при и расходится при .

Пример 2. Ряд вида

(1.3)

называется гармоническим.

Запишем частичную сумму этого ряда:

.

Сумма больше суммы,
представленной следующим образом:

или .

Если , то , или .

Следовательно, если , то ,
т.е. гармонический ряд расходится.

Пример 3. Ряд вида

(1.4)

называется обобщенным гармоническим.

Если , то
данный ряд обращается в гармонический ряд,
который является расходящимся.

Если , то
члены данного ряда больше соответствующих
членов гармонического ряда и, значит, он
расходится. При имеем геометрический ряд, в котором ; он является
сходящимся.

Итак, обобщенный гармонический ряд сходится
при и
расходится при .

1.3. Необходимый и достаточные признаки
сходимости.

Необходимый признак сходимости ряда.

Ряд может
сходиться только при условии, что его общий член при
неограниченном увеличении номера стремится к нулю: .

Если , то
ряд
расходится – это достаточный признак
расходимости ряда.

Достаточные признаки сходимости ряда с
положительными членами.

Признак сравнения рядов с положительными
членами.

Исследуемый ряд сходится, если его члены не
превосходят соответствующих членов другого,
заведомо сходящегося ряда; исследуемый ряд
расходится, если его члены превосходят
соответствующие члены другого, заведомо
расходящегося ряда.

Признак Даламбера.

Если для ряда с положительными членами

выполняется условие , то ряд сходится при и расходится при .

Признак Даламбера не дает ответа, если . В этом случае
для исследования ряда применяются другие приемы.

Упражнения.

Записать ряд по его заданному общему члену:

;

;

.

Решение.

Полагая ,,,…, имеем бесконечную
последовательность чисел:

,,. Сложив его члены, получим
ряд

.

Поступая так же, получим ряд

.

Придаваязначения
1,2,3,… и учитывая, что,,,…, получим ряд

.

Найти n-ый член ряда по его данным первым
членам:

;

.

Решение.

Знаменатели членов ряда, начиная с первого,
являются четными числами; следовательно, n-ый
член ряда имеет вид .

Числители членов ряда образуют натуральный ряд
чисел, а соответствующие им знаменатели –
натуральный ряд чисел, а соответствующие им
знаменатели – натуральный ряд чисел, начиная с 3.
Знаки чередуются по закону или по закону . Значит, n-й член ряда
имеет вид . или .

Исследовать сходимость ряда, применяя
необходимый признак сходимости и признак
сравнения:

;

;

.

Решение.

Находим .

Необходимый признак сходимости ряда
выполняется, но для решения вопроса о сходимости
нужно применить один из достаточных признаков
сходимости. Сравним данный ряд с геометрическим
рядом

,

который сходится, так как.

Сравнивая члены данного ряда, начиная со
второго, с соответствующими членами
геометрического ряда, получим неравенства

т.е. члены данного ряда, начиная со второго,
соответственно меньше членов геометрического
ряда, откуда следует, что данный ряд сходится.

Имеем

.

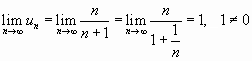
Здесь выполняется достаточный признак
расходимости ряда; следовательно, ряд
расходится.

Находим .

Необходимый признак сходимости ряда
выполняется. Сравним данный ряд с обобщенным
гармоническим рядом

,

который сходится, поскольку, следовательно, сходится и
данный ряд.

Исследовать сходимость ряда, используя признак
Даламбера:

;

.

Решение.

Подставив в общий член ряда вместо n число n+1, получим
. Найдем
предел отношения -го члена к n-му члену при :

.

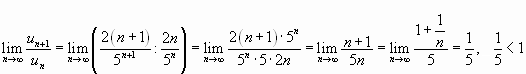
Следовательно, данный ряд сходится.

Имеем

Значит, данный ряд расходится.

, т.е. ряд
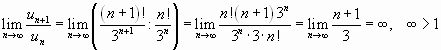
расходится.

II. Знакопеременный ряд

2.1 Понятие знакопеременного ряда.

Числовой ряд

называется знакопеременным, если среди
его членов имеются как положительные, так и
отрицательные числа.

Числовой ряд называется знакочередующимся,
если любые два стоящие рядом члена имеют
противоположные знаки.

,

где для
всех (т.е. ряд,
положительные и отрицательные члены которого
следуют друг за другом поочередно). Например,

;

;

.

Для знакочередующихся рядов имеет место
достаточный признак сходимости (установленный в
1714г. Лейбницем в письме к И.Бернулли).

2.2 Признак Лейбница. Абсолютная и условная
сходимость ряда.

Теорема (Признак Лейбница).

Знакочередующийся ряд сходится, если:

Последовательность абсолютных величин членов
ряда монотонно убывает, т.е. ;

Общий член ряда стремится к нулю:.

При этом сумма S ряда удовлетворяет
неравенствам

.

Замечания.

Исследование знакочередующегося ряда вида

(с отрицательным первым членом) сводится путем
умножения всех его членов на к исследованию ряда .

Ряды, для которых выполняются условия теоремы
Лейбница, называются лейбницевскими (или
рядами Лейбница).

Соотношение позволяет получить простую и удобную
оценку ошибки, которую мы допускаем, заменяя
сумму S данного ряда его частичной суммой .

Отброшенный ряд (остаток) представляет собой
также знакочередующийся ряд , сумма которого по модулю меньше
первого члена этого ряда, т.е.. Поэтому ошибка меньше модуля первого из
отброшенных членов.

Пример. Вычислить приблизительно сумму ряда .

Решение: данный ряд Лейбницевского типа. Он
сходится. Можно записать:

.

Взяв пять членов, т.е. заменивна

, сделаем
ошибку, меньшую,

чем. Итак,.

Для знакопеременных рядов имеет место
следующий общий достаточный признак сходимости.

Теорема. Пусть дан знакопеременный ряд

.

Если сходится ряд

,

составленный из модулей членов данного ряда, то
сходится и сам знакопеременный ряд.

Признак сходимости Лейбница для
знакочередующихся рядов служит достаточным
признаком сходимости знакочередующихся рядов.

Знакопеременный ряд называется абсолютно
сходящимся, если сходится ряд, составленный
из абсолютных величин его членов, т.е. всякий
абсолютно сходящийся ряд является сходящимся.

Если знакопеременный ряд сходится, а
составленный из абсолютных величин его членов
ряд расходится, то данный ряд называется условно
(неабсолютно) сходящимся.

2.3. Упражнения.

Исследовать на сходимость (абсолютную или
условную) знакочередующийся ряд:

;

Решение.

Члены данного ряда по абсолютной величине
монотонно убывают:

и

Следовательно, согласно признаку Лейбница, ряд
сходится. Выясним, сходится ли этот ряд абсолютно
или условно.

Ряд ,
составленный из абсолютных величин данного ряда,
является гармоническим рядом, который,
расходится. Поэтому данный ряд сходится условно.

Решение.

Члены данного ряда по абсолютной величине
монотонно убывают:

, но

.

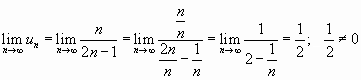
Ряд расходится, так как признак Лейбница не
выполняется.

;

Решение.

Используя признак Лейбница, получим

;,

т.е. ряд сходится.

Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда:

.

Это геометрический ряд вида, где, который сходится. Поэтому данный ряд
сходится абсолютно.

;

Решение.

Используя признак Лейбница, имеем

;

, т.е. ряд
сходится.

Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда:

, или

.

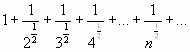
Это обобщенный гармонический ряд, который
расходится, так как. Следовательно, данный ряд сходится
условно.

III. Функциональный ряд

3.1. Понятие функционального ряда.

Ряд, членами которого являются функции от , называется функциональным:

.

Придавая
определенное значение , получим числовой ряд

,

который может быть как сходящимся, так и
расходящимся.

Если полученный числовой ряд сходится, то точка
называется точкой
сходимости функционального ряда; если же ряд
расходится – точкой расходимости
функционального ряда.

Совокупность числовых значений аргумента , при которых
функциональный ряд сходится, называется его областью
сходимости.

В области сходимости функционального ряда его
сумма является некоторой функцией от :.

Определяется она в области сходимости
равенством

, где

– частичная
сумма ряда.

Пример. Найти область сходимости ряда .

Решение. Данный ряд является рядом
геометрической прогрессии со знаменателем . Следовательно,
этот ряд сходится при , т.е. при всех ; сумма ряда равна ;

, при .

3.2. Степенные ряды.

Степенным рядом называется ряд вида

,

где числа
называются коэффициентами ряда, а член – общим членом
ряда.

Областью сходимости степенного ряда
называется множество всех значений , при которых данный ряд
сходится.

Число называется радиусом
сходимости степенного ряда, если при ряд сходится и
притом абсолютно, а при ряд расходится.

Радиус сходимости
найдем, используя признак Даламбера:

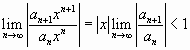
(не зависит от),

,

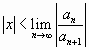
т.е. если степенной ряд сходится при любых ,
удовлетворяющих данному условию и расходится
при .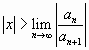

Отсюда следует, что если существует предел

,

то радиус сходимости рядаравен этому пределу и степенной
ряд сходится при , т.е. в промежутке , который называется промежутком
(интервалом) сходимости.

Если , то
степенной ряд сходится в единственной точке .

На концах промежутка ряд может сходиться
(абсолютно или условно), но может и расходиться.

Сходимость степенного ряда при и исследуется с помощью
какого-либо из признаков сходимости.

3.3. Упражнения.

Найти область сходимости ряда:

;

Решение. Найдем радиус сходимости данного
ряда:

.

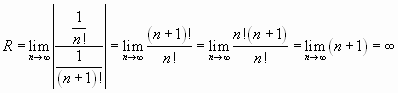
Следовательно, данный ряд абсолютно сходится
на всей числовой оси.

Решение. Воспользуемся признаком Даламбера.
Для данного ряда имеем:

,,

.

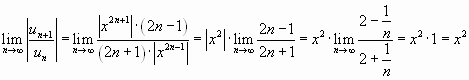
Ряд абсолютно сходится, если или . Исследуем поведение ряда на
концах интервала сходимости.

При имеем
ряд , который
сходится по признаку Лейбница.

При имеем
ряд– это тоже
сходящийся Лейбницевский ряд. Следовательно,
областью сходимости исходного ряда является
отрезок.

.

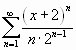
Решение. Найдем радиус сходимости ряда:

.

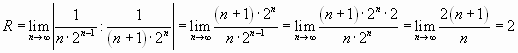
Следовательно, ряд сходится при, т.е. при.

Приимеем
ряд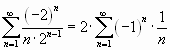, который
сходится по признаку Лейбница.

Приимеем
расходящийся ряд

.

Следовательно, областью сходимости исходного
ряда является промежуток.

IV. Разложение элементарных функций в ряд
Маклорена.

Для приложений важно уметь данную функцию разлагать в
степенной ряд, т.е. функцию представлять в виде суммы
степенного ряда.

Рядом Тейлора для функции называется степенной ряд
вида

.

Если , то
получим частный случай ряда Тейлора

,

который называется рядом Маклорена.

Степенной ряд внутри его промежутка сходимости
можно почленно дифференцировать и интегрировать
сколько угодно раз, причем полученные ряды имеют
тот же промежуток сходимости, что и исходный ряд.

Два степенных ряда можно почленно складывать и
умножать по правилам сложения и умножения
многочленов. При этом промежуток сходимости
полученного нового ряда совпадает с общей частью
промежутков сходимости исходных рядов.

Для разложения функции в ряд Маклорена необходимо:

Вычислить значения функции и ее
последовательных производных в точке , т.е.,,,…,;

Составить ряд Маклорена, подставив значения
функции и ее последовательных производных в
формулу ряда Маклорена;

Найти промежуток сходимости полученного ряда
по формуле

, .

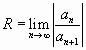
Таблица, содержащая разложения в ряд
Маклорена некоторых элементных функций:

.

.

.

.

.

.

Пример 1. Разложить в ряд Маклорена функцию.

Решение. Так как , то, заменяя на
в разложении ,
получим:

, .

Пример 2. Выписать ряд Маклорена функции .

Решение. Так как , то воспользовавшись формулой , в которой
заменим на , получим:

,

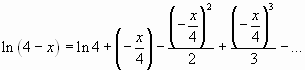
или

,

если

, т.е..

Пример 3. Разложить в ряд Маклорена функцию .

Решение. Воспользуемся формулой . Так как

, то
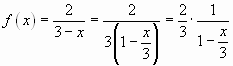
заменивнаполучим:

, или

,

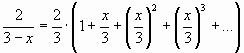
где , т.е. .

V. Практические задания для самоконтроля
студентов.

При помощи признака сравнения рядов установить
сходимость

или расходимость рядов:

.

.

.

.

.

Исследовать по признаку Даламбера сходимость
рядов:

.

.

.

.

.

Исследовать на сходимость (абсолютную или
условную) знакочередующийся ряд:

.;

.;

.;

.;

.

Найти промежутки сходимости нижеследующих
рядов и выяснить вопрос об их сходимости на
концах промежутков сходимости:

;

;

;

;

.

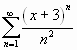
Используя разложения в ряд Маклорена функции,,,,
разложить степенные ряды функции:

.

.

.

.

.

VI. Ответы

I.

1. сходится;
2. расходится;
3. сходится;
4. сходится;
5. расходится;
6. сходится;
7. сходится;
8. расходится;
9. сходится;
10. сходится.

II.

1. cходится абсолютно;
2. cходится абсолютно;
3. cходится условно;
4. cходится условно;
5. cходится абсолютно.

III.

1. ;
2. ;
3. ;
4. ;
5. .

IV.

;

;

;

;

VII. Историческая справка.

Решение многих задач сводится к вычислению
значений функций и интегралов или к решению
дифференциальных уравнений, содержащих
производные или дифференциалы неизвестных
функций.

Однако точное выполнение указанных
математических операций во многих случаях
оказывается весьма затруднительным или
невозможным. В этих случаях можно получить
приближенное решение многих задач с любой
желаемой точностью при помощи рядов.

Ряды представляют собой простой и совершенный
инструмент математического анализа для
приближенного вычисления функций, интегралов и
решений дифференциальных уравнений.

Теория рядов создавалась в тесной связи с
теорией приближенного представления функций в
виде многочленов. Впервые это сделал И. Ньютон (1642
– 1727). в 1676г. В его письме к секретарю Лондонского
Королевского Общества появилась формула:

,

которую мы знаем как формулу бинома Ньютона.

Здесь мы видим функцию , представленную в виде
многочлена. Но если число не является натуральным, в
правой части равенства получается не полином, а
бесконечная сумма слагаемых, то есть ряд.

Развивая идею Ньютона, английский математик
Брук Тейлор (1685 – 1731) в 1715г. доказал, что любой
функции, имеющей в точке производные всех порядков, можно
сопоставить ряд:

.

Мы не можем пока поставить знак равенства между
функцией ,
принимающей конечное значение для любого
значения , и
стоящим справа функциональным рядом.

Для того, чтобы вместо знака “” можно было поставить
знак равенства, необходимо провести некоторые
дополнительные рассуждения, связанные именно с
бесконечностью числа слагаемых в правой части
равенства и касающиеся области сходимости ряда.

При
формула Тейлора принимает вид, в котором
называется формулой Маклорена:

.

Колин Маклорен (1698 – 1746), ученик Ньютона, в
работе “Трактат о флюксиях” (1742) установил, что
степенной ряд, выражающий аналитическую функцию,
– единственный, и это будет ряд Тейлора,
порожденный такой функцией. В формуле бинома
Ньютона коэффициенты при степенях представляют собой
значения ,
где .

Итак, ряды возникли в XVIII в. как способ
представления функций, допускающих бесконечное
дифференцирование. Однако функция,
представляемая рядом, не называлась его суммой, и
вообще в то время не было еще определено, что
такое сумма числового или функционального ряда,
были только попытки ввести это понятие.

Например, Л. Эйлер (1707-1783), выписав для функции
соответствующий ей степенной ряд, придавал
переменной
конкретное значение . Получался числовой ряд. Суммой этого
ряда Эйлер cчитал значение исходной функции в
точке . Но это
не всегда верно.

О том, что расходящийся ряд не имеет суммы,
ученые стали догадываться только в XIX в., хотя в
XVIII в. многие, и прежде всего Л. Эйлер, много
работали над понятиями сходимости и
расходимости. Эйлер называл ряд сходящимся, если его общий
член
стремится к нулю при возрастании .

В теории расходящихся рядов Эйлер получил
немало существенных результатов, однако
результаты эти долго не находили применения. Еще
в 1826г. Н.Г. Абель (1802 – 1829) называл расходящиеся
ряды “дьявольским измышлением”. Результаты
Эйлера нашли обоснование лишь в конце XIX в.

В формировании понятия суммы сходящегося ряда
большую роль сыграл французский ученый О.Л. Коши
(1789 – 1857); он сделал чрезвычайно много не только в
теории рядов, но и теории пределов, в разработке
самого понятия предела. В 1826г. Коши заявил, что
расходящийся ряд не имеет суммы.

В 1768г. французский математик и философ Ж.Л.
Д’Аламбер исследовал отношение последующего
члена к предыдущему в биномиальном ряде и
показал, что если это отношение по модулю меньше
единицы, то ряд сходится. Коши в 1821г. доказал
теорему, излагающую в общем виде признак
сходимости знакоположительных рядов, называемых
теперь признаком Д’Аламбера.

Для исследования сходимости знакочередующихся
рядов используется признак Лейбница.

Г.В. Лейбниц (1646 – 1716), великий немецкий
математик и философ, наряду с И. Ньютоном
является основоположником дифференциального и
интегрального исчисления.

Список литературы:

Основная:

1. Богомолов Н.В., Практические занятия по
   математике. М., “Высшая школа”, 1990 – 495 с.;
2. Тарасов Н.П., Курс высшей математики для
   техникумов. М., “Наука”, 1971 – 448 с.;
3. Зайцев И.Л., Курс высшей математики для
   техникумов. М., государственное издательство
   техникумов – теоретической литературы, 1957 – 339 с.;
4. Письменный Д.Т., Курс лекций по высшей
   математике. М., “Айрис Пресс”, 2005, часть 2 – 256 с.;
5. Выгодский М.Я., Справочник по высшей математике.
   М., “Наука”, 1975 – 872 с.;

Дополнительная:

1. Гусак А.А., Высшая математика. В 2-х т., Т.2: Учебное
   пособие для студентов вузов. Мос.,
   “ТетраСистемс”, 1988 – 448 с.;
2. Григулецкий В.Г., Лукьянова И.В., Петунина И.А.,
   Математика для студентов экономических
   специальностей. Часть 2. Краснодар, 2002 – 348 с.;
3. Григулецкий В.Г. и др. Задачник-практикум по
   математике. Краснодар. КГАУ, 2003 – 170 с.;
4. Григулецкий В.Г., Степанцова К.Г., Гетман В.Н.,
   Задачи и упражнения для студентов
   учетно-финансового факультета. Краснодар. 2001 – 173
   с.;
5. Григулецкий В.Г., Ященко З.В., Высшая математика.
   Краснодар, 1998 – 186 с.;
6. Малыхин В.И., Математика в экономике. М.,
   “Инфра-М”, 1999 – 356с.