В статье обсуждаются различные формулы и задачи о том, как найти импульс после столкновения.
Скорость объекта изменяется во время столкновения из-за внешней силы от другого объекта. Изменение скорости вызывает изменение количества движения после столкновения. Итак, мы можем найти импульс после столкновения, используя формулу импульса, законы сохранения количества движения и сохранения энергии.
Импульс перед столкновением Pi = му. Импульс после столкновения также определяется путем оценки изменения скорости v объекта после столкновения. пf = мв
Узнать больше о Momentum.
Предположим, что неподвижный шар массой 8 кг сталкивается с другим шаром. После столкновения мяч движется со скоростью 5 м / с. Определите импульс мяча для пула после столкновения.
Данный:
m = 8 кг
v = 5 м / с
Найти: ∆P =?
Формула:
∆Р = Рf – Пi
Решения:
Импульс шара после столкновения рассчитывается как,
∆Р = Рf – Пi
∆P = mv – mu
Поскольку бильярдный шар в состоянии покоя, т. Е. U = 0
∆P = мв
Подставляя все значения,
∆P = 8 х 5
∆P = 40
Импульс бильярдного шара после столкновения составляет 40 кгм / с.
Узнайте больше о том, как найти чистую силу от Momentum.
Как найти импульс после формулы столкновения?
Импульс после столкновения определяется по формуле импульса.
Когда мы говорим о нахождении импульса после столкновения только одного объекта, мы можем вычислить его, используя формулу импульса. Импульс – это изменение импульса после столкновения из-за внешней силы. Поскольку столкновения происходят быстро, сложно отдельно рассчитать приложенную внешнюю силу и время.
Как только мы вычислили импульс до Pi и после столкновения Pf, мы можем найти импульс с точки зрения внешней силы со стороны другого объекта как,
Импульс (ΔP) – произведение внешней силы F и разницы во времени (∆t) в котором происходит изменение импульса ».
Математически,
∆P = F ∆t
Pf – Пi = F∆t
Подробнее о Типах сил.
Футбольный мяч ударил мячом массой 5 кг по поверхности земли без трения с силой 30 Н в течение 5 секунд. Какова скорость и импульс футбола после удара ногой?
Данный:
m = 5 кг
Ф = 30 Н
∆t = 5 с
Найти:
- v2=?
- Pf=?
Формула:
- Р = мв
- ∆P = F ∆t
Решения:
Импульс футбола до удара ногой:
Pi = м1v1
Поскольку футбол отдыхает. т.е. v1=0
Следовательно, Pi = 0
Импульс футбола до удара ногой равен нулю.
Импульс футбольного мяча после удара ногой рассчитывается с использованием Формула импульса.
∆P = F ∆t
Pf-Pi = F∆t
Поскольку Pi = 0
Pf = F∆t
Подставляя все значения,
Pf = 30 x 5
Pf = 150
Импульс футбола после удара ногой – 150 кг.⋅м/с
Скорость футбола после удара ногой равна,
m2v2 = 150
v2 = 150 / 5
v2 = 30
Скорость футбольного мяча после удара ногой составляет 30 м / с.
Узнайте больше о том, как найти Net Force?
Как определить суммарный импульс двух объектов после столкновения?
Полный импульс двух объектов после столкновения оценивается с помощью закона сохранения количества движения.
Когда два объекта сталкиваются, их соответствующий импульс изменяется из-за их скорости, но их общий импульс после столкновения остается неизменным. Полный импульс после столкновения суммируется путем сложения всех соответствующих импульсов сталкивающихся объектов.
В закрытой или изолированной системе, когда два объекта, обладающие разными массами и скоростями, сталкиваются, они могут перемещаться друг с другом или далеко, в зависимости от типов столкновения – например, неупругое столкновение or упругое столкновение.
(Кредит: Shutterstock)
После столкновения их импульс, который является произведение их масс и скоростей, тоже разнообразно. Но если говорить об общем импульс изолированной системы, остается без изменений. Во время при столкновении любой импульс, который теряет один объект, приобретается другим объектом. Так сохраняется общий импульс сталкивающихся объектов.
Предположим, что импульс объекта 1 равен P1 = м1u1
Импульс объекта 2 равен P2 = м2u2
Импульс обоих объектов до столкновения Pi = P1 + Р2 = м1u1 + м2+u2
Если во время столкновения нет действующей силы, то импульс Pf обоих объектов после столкновения остается таким же, как и до столкновения.
Следовательно, согласно закон сохранения импульса,
Pi = Pf
m1u1 + м2+u2 = м1v1 + м2+v2 ……………………. (*)
Обратите внимание, что скорости обоих объектов изменились после столкновения с u на v. Это показывает, что их соответствующий импульс после столкновения также изменился.
Для изолированная система,
«Полный импульс после столкновения точно такой же, как до столкновения, в соответствии с законом сохранения количества движения».
(Кредит: Shutterstock)
Предположим, что две мраморные гальки массой 10 кг и 5 кг движутся со скоростью 8 м / сек и 12 м / сек соответственно; сталкиваются друг с другом. После столкновения оба камешка удаляются друг от друга с одинаковой массой. Если один камешек удаляется со скоростью 10 м / сек, какова скорость второго?
Данный:
m1 = 10 кг
m2 = 5 кг
u1= 8 м / сек
u2= 12 м / сек
v1= 10 м / сек
Найти: v2 =?
Формула:
m1u1 + м2+u2 = м1v1 + м2+v2
Решения:
Закон закон сохранения импульса вычисляет скорость второй камешек,
Для изолированных систем, когда нет равнодействующая сила действует,
m1u1 + м2+u2 = м1v1 + м2+v2
Обратите внимание, что вторые объекты перемещаются напротив первого объекта. Следовательно, импульс второго объекта должен быть отрицательным.
Подставляя все значения,
10 x 8 + (- (5 x12) = 10 x 10 + (- (5xv2)
80 – 60 = 100 -5v2
5v2 = 100-20
v2 = 80 / 5
v2 = 16
Скорость второго камешка после столкновения составляет 16 м / сек.
Узнайте больше об относительной скорости.
Как найти импульс после упругого столкновения?
Импульс после упругого столкновения оценивается с помощью закона сохранения энергии.
Общая импульс сохраняется при столкновении. Кинетическая энергия соответствующего объекта может измениться после столкновения, но полная кинетическая энергия после упругого столкновения остается неизменной. Итак, мы можем найти импульс после упругого удара, используя закон сохранения энергии.
(Кредит: Shutterstock)
Когда столкновение между объектами является упругим, полная кинетическая энергия сохраняется.
Согласно закон сохранения энергии,
Переставляем уравнение (*) с помощью членов с m1 с одной стороны и членов с m2 с другой.
Теперь переставим уравнение (#), используя члены с m1 на одной стороне и члены с m2 на другой, и сократим ½ общего множителя,
Узнаем, что первый член слева равен «1» в приведенном выше уравнении, мы получаем.
………………. (1)
Подставьте приведенное выше уравнение в уравнение (*), чтобы исключить v2, мы получаем
Наконец измените приведенное выше уравнение и решите для скорость v1 объекта 1 после столкновения,
Подставьте приведенное выше уравнение в уравнение (1) скорость v2 объекта 2 после столкновения,
Узнайте больше о кинетической энергии.
Когда мяч массой 10 кг, движущийся со скоростью 2 м / с, упруго сталкивается с другим мячом массой 2 кг, движущимся в противоположном направлении со скоростью 4 м / с. Рассчитайте конечные скорости обоих шариков после упругого столкновения.
Данный:
m1 = 10 кг
m2 = 2 кг
u1 = 2 м / с
u2 = -4 м / с
Найти:
- v1 =?
- v2 =?
Формула:
Решения:
Скорость шара 1 после упругого столкновения рассчитывается как
Подставляя все значения,
v1 = 0
Это означает, что упругий удар остановил мяч 1.
Скорость шара 2 после упругого столкновения рассчитывается как
Подставляя все значения,
v2= 6 м / с
Это означает, что упругое столкновение изменяет скорость второго мяча до 6 м / с.
Как найти импульс после неупругого столкновения?
Импульс после столкновения определяется с помощью закона сохранения количества движения.
Полный импульс сохраняется во время столкновения. Но полная кинетическая энергия системы также изменяется, как и кинетическая энергия соответствующего объекта, и столкновение называется неупругим. Итак, мы можем найти импульс после неупругого столкновения, используя закон сохранения количества движения.
Если столкновение упругое, оба объекта удаляются друг от друга с разной скоростью v1, v2 в противоположных направлениях.
Но если столкновение неупругое, оба объекта движутся с одной конечной скоростью V в одном и том же направлении.
Следовательно, импульс Pf после неупругое столкновение становится м1В + м2V или V (м1+m2)
Итак, уравнение сохранение импульса при неупругом столкновении является,
m1u1 + м2+u2 = V (м1+m2)
Формула для окончательный скорость после неэластичный столкновение является,
V=(м1u1 + м2+u2) / (м1+m2)
Узнайте больше о скорости.
Два мальчика играют на детской площадке в парке. Первый мальчик массой 20 кг скользил по горке со скоростью 10 м / с. Поскольку первый мальчик на определенных участках становится медленнее, в последнее время он сталкивается с другим мальчиком массой 30 кг, который скользит вниз со скоростью 12 м / с. С какой скоростью оба мальчика соскользнут вместе после столкновения?
Данный:
m1 = 20 кг
m2 = 30 кг
u1 = 10 м / с
u2 = 12 м / с
Найти: В =?
Формула:
V=(м1u1 + м2+u2) / (м1+m2)
Решения:
Конечная скорость скольжения обоих мальчиков после столкновения рассчитывается как
V=(м1u1 + м2+u2) / (м1+m2)
Подставляя все значения,
V = 11.2
Конечная скорость скольжения обоих мальчиков после неупругого столкновения составляет 11.2 м / с.
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
p — импульс тела [кг · м/с]
m — масса тела [кг]
v — скорость [м/с]
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
pn — импульс тела [кг · м/с]
Простая задачка
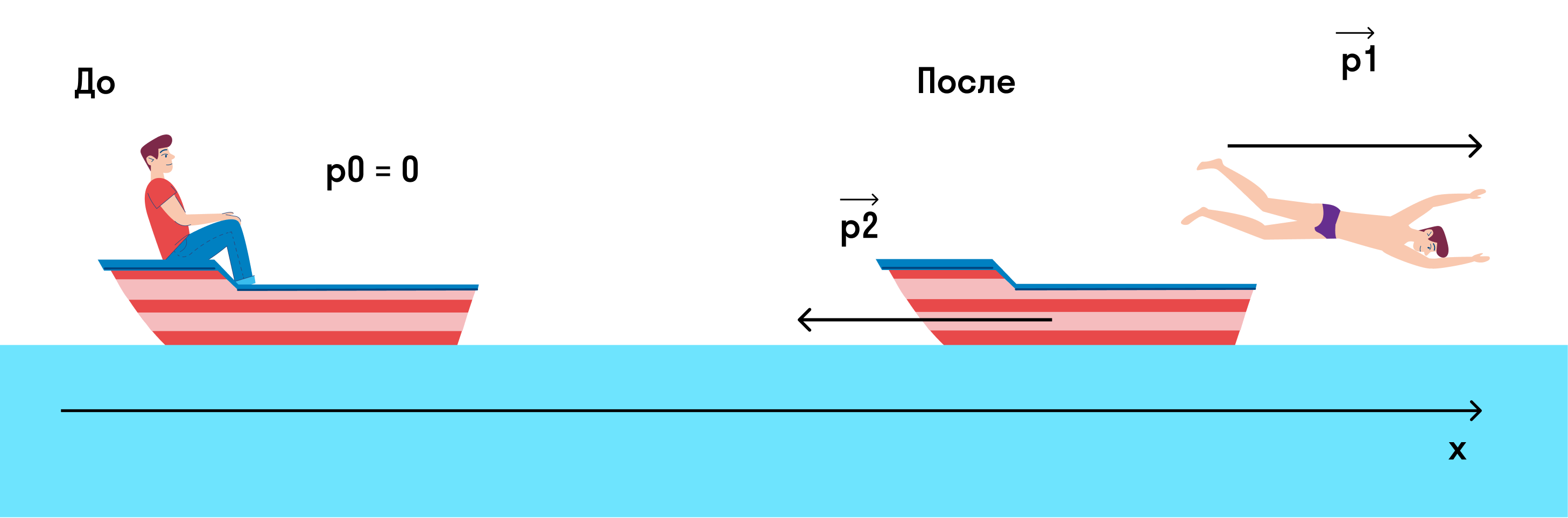
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
— это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
— это импульс мальчика после прыжка,
— это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
Подставим формулу импульса.
, где:
— масса мальчика [кг]
— скорость мальчика после прыжка [м/с]
— масса лодки [кг]
— скорость лодки после прыжка [м/с]
Выразим скорость лодки
:
Подставим значения:
м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
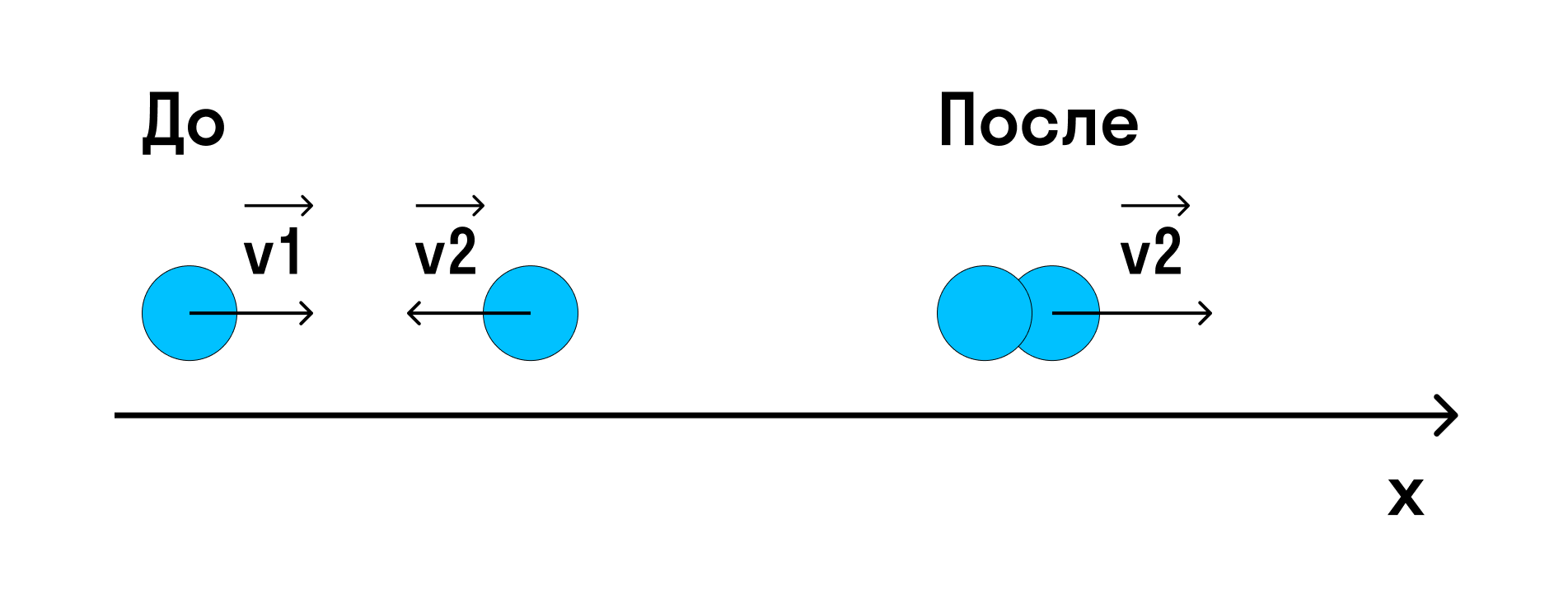
Тело массы m1 = 800 г движется со скоростью v1 = 3 м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы
, которое движется с искомой скоростью:
Отсюда находим скорость тела, образовавшегося после удара:
Переводим массу в килограммы и подставляем значения:
м/с
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
В этих уравнениях слева находится величина a. Так как левые части уравнений равны, можно приравнять правые их части
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится
— это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
Подставляем:
Или, сокращенно:
То есть, вектор
– это вектор изменения импульса
.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила
называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг · vг = mр · vр,
где mг — это масса горючего,
vг — скорость горючего,
mр — масса ракеты,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
vр = mг · vг / mр
Скорость ракеты при реактивном движении
vр = mг · vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
vр — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Как определить суммарный импульс?
Чему равен суммарный
импульс двух тел одинаковой массы m, двигавшихся с
одинаковыми по модулю скоростями v во взаимно
перпендикулярных направлениях, после неупругого удара?
Решение.
При абсолютно неупругом
ударе выполняется закон сохранения импульса. После такого удара тела движутся
как одно целое с общей скоростью.
Используя закон сохранения импульса получим,
что суммарный импульс шаров mv1 + mv2 = p. Из рисунка найдем по теореме Пифагора модуль суммарного
импульса.
p = mv^2.
Ответ: p = mv^2.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 19.9k
Рассмотрим изменение импульсов тел при их взаимодействии друг с другом.
Если два или несколько тел взаимодействуют только между собой (то есть не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.
Импульс, равный векторной сумме импульсов тел, входящих в замкнутую систему, называется суммарным импульсом этой системы.
Результирующая векторная величина импульса системы тел равна векторной сумме импульсов тел, её составляющих:
Закон сохранения импульса
Суммарный импульс системы тел до взаимодействия равен суммарному импульсу этой системы тел после взаимодействия.
В этом заключается закон сохранения импульса, который называют также законом сохранения количества движения.
Закон сохранения импульса впервые был сформулирован Р. Декартом. В одном из своих писем он написал:
«Я принимаю, что во Вселенной, во всей созданной материи есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает».
Для примера возьмем систему из двух тел: шары массами
m1
и
m2
равномерно и прямолинейно движутся со скоростями
v1
и
v2
, причем их скорости противоположно направлены, то есть шары движутся навстречу друг другу. Импульсы шаров записываются
p1→=m1v1→
и
p2→=m2v2→
соответственно.
Рис. (1). Направление движения шаров до соударения
Когда шары приблизятся друг к другу, произойдет столкновение. Удар не будет мгновенным, он займёт пусть малое, но вполне измеримое время (t), при этом появятся силы взаимодействия
F1→
и
F2→
, которые будут приложены к первому и второму шарам соответственно. Как известно, под действием силы скорость тела меняется, поэтому изменятся и скорости шаров. После столкновения модули и направления скоростей могут быть совершенно иными, поэтому обозначим скорости
v1′
и
v2′
соответственно. Изменятся и импульсы шаров, они станут равны
p1→′=m1v1→′
и
p2→′=m2v2→′
соответственно.
Рис. (2). Направление движения шаров после соударения
Тогда, согласно закону сохранения импульса, имеют место равенства:
или
.
Данные равенства являются математической записью закона сохранения импульса.
Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю.
Таким образом, более точно закон сохранения импульса формулируется так:
векторная сумма импульсов всех тел замкнутой системы — величина постоянная, если внешние силы, действующие на неё, отсутствуют или же их векторная сумма равна нулю.
Импульс системы тел может измениться только в результате действия на систему внешних сил. И тогда закон сохранения импульса действовать не будет.
Пример:
при стрельбе из пушки возникает отдача: снаряд летит вперёд, а само орудие откатывается назад. Почему?
Рис. (3). После выстрела пушка откатывается назад
Снаряд и пушка — замкнутая система, в которой действует закон сохранения импульса. В результате выстрела из пушки импульс самой пушки и импульс снаряда изменятся. Но сумма импульсов пушки и находящегося в ней снаряда до выстрела останется равной сумме импульсов откатывающейся пушки и летящего снаряда после выстрела.
Обрати внимание!
В природе замкнутых систем не существует. Но если время действия внешних сил очень мало, например, во время взрыва, выстрела и т. п., то в этом случае воздействием внешних сил на систему пренебрегают, а саму систему рассматривают как замкнутую.
Кроме того, если на систему действуют внешние силы, но сумма их проекций на одну из координатных осей равна нулю (то есть силы уравновешены в направлении этой оси), то в этом направлении закон сохранения импульса выполняется.
Великий учёный Исаак Ньютон изобрёл наглядную демонстрацию закона сохранения импульса — маятник, или её ещё называют «колыбель». Это устройство представляет собой конструкцию из пяти одинаковых металлических шаров, каждый из которых крепится с помощью двух тросов к каркасу, а тот в свою очередь — к прочному основанию П-образной формы.
Рис. (4). Устройство для демонстрации закона сохранения импульса, колыбель Ньютона
Маятник Ньютона устроен так, что начальный шар передаёт импульс второму шарику, а затем замирает. Нашему глазу на первый взгляд не заметно, как следующий шарик принимает импульс от предыдущего, мы не можем проследить его скорость. Но, если взглянуть пристальнее, можно заметить, как шарик немножко «вздрагивает». Это объясняется тем, что он совершает движения с посланной ему скоростью, но поскольку расстояние очень маленькое, ему некуда разогнаться, то он может на своём коротком пути передать импульс третьему шарику и в итоге остановиться.
Такое же действие совершает и следующий шарик и т. д. Последнему шарику некуда передавать свой импульс, поэтому он свободно колеблется, поднимаясь на определённую высоту, а затем возвращается, и весь процесс передачи импульсов повторяется в обратном порядке.
Самый яркий пример применения закона сохранения импульса — реактивное движение.
Рис. (4). Шаттл
Источники:
Рис. 1. Направление движения шаров до соударения. © ЯКласс.
Рис. 2. Направление движения шаров после соударения. © ЯКласс.
Рис. 3. После выстрела пушка откатывается назад. © ЯКласс. Пушка. Указание автора не требуется, 2021-08-26, Pixabay License, https://pixabay.com/images/id-159503/
Рис. 4. Устройство для демонстрации закона сохранения импульса, колыбель Ньютона.Указание автора не требуется, 2021-08-26, Pixabay License,https://pixabay.com/images/id-6076266/.
Рис. 5. Шаттл. Указание автора не требуется, 2021-08-26, Pixabay License,https://pixabay.com/images/id-992/