Ответы на вопросы будут следующие:
1) Для определения суммарного объёма компонентов раствора необходимо воспользоваться формулой: V = m : p, где V – это объём, m – масса, а p соответственно плотность. В нашем случае формула будет выглядеть так:

Прежде чем приступать к расчётам, необходимо массу воды (в) и глицерина (г) перевести в граммы, так как плотность в условии задачи измеряется в г/см3! Рассчитываем суммарный объём компонентов смеси:

2) Для нахождения плотности тела, используется формула: p = m : V. Для решения нашей задачи с мылом, формула подсчёта плотности будет выглядеть так:

Следовательно расчётная плотность раствора буде такой:

3) Теперь необходимо определить объём полученного раствора:

Таким образом, получается, что если из объёма полученного раствора вычесть суммарный объём компонентов смеси (Vр – V), то разница составит приблизительно 17 миллилитров.
Сегодня буду хулиганить, как хочу 😜 (в пределах разумного, конечно 😊). С чего бы это? Объясняю: первая причина – мои ученики, вторая причина – их школьные учителя. Теперь, более подробно.
Ученики 😘 должны иметь интерес к изучаемому предмету. Я не о химии вообще. Это яркая, замечательная наука, если рассматривать ее экспериментальную часть. Я о задачах по химии. Многие ребята не решают задачи, поскольку считают их сложными, скучными, непонятными. Перед родителями встает вопрос: “Как любимую зайку, лапушку, солнышко заставить готовиться к ЕГЭ по химии?!” А никак. Вы никогда не заставите учить предмет, как бы не старались. Насильно мил не будешь. Даже если вы найдете самого дорогого репетитора, заплатите ему бешеные деньги, привяжете ребенка к креслу и поставите рядом вооруженную охрану, ребенок будет только делать вид, что он слушает учителя и усердно учится. А сам будет прокручивать в голове совсем другие мысли, типа: “Чтобы ты, зараза, сдохла! Как я тебя ненавижу!” Как быть? Давайте вспомним себя в детстве. Что у нас было в голове до 18 лет? Правильно. Ветер майский пел нам песни и менял свое направление каждый день. Чем развлекается майский ветер? Блестящим фантиком, который беззаботно машет своими бумажными крылышками. В этот момент делай с ветром, что хочешь. Так и с ребенком. Если поманить его интересной формой и дать понятное, разложенное по полочкам, содержание, сердце “ветра” растает и задачи по химии превратятся в любимейшее занятие. Это много раз проверено на моем 30-ти летнем опыте работы. Поэтому я постоянно ищу новые фантики, а содержание у меня уже давным-давно отработано и разложено по полочкам.
Школьные учителя моих учеников 😡 – еще та категория читателей, особенно, старые бабушки-химички и дедушки-химичи. Лично у меня уже закончился словарный запас приличных слов, а неприличные слова писать запрещается (произносить их тоже нельзя, можно только в мыслях). Уважаемые коллеги (🤬 пи-пи-пи), я именно к вам (🤬 пи-пи-пи) обращаюсь, прежде чем писать (🤬 пи-пи-пи) комментарии, прочитайте хотя бы школьные учебники, чтобы не получилось вот так:
Однако, вернемся к основной теме. В статье “Секретная шпаргалка по химии. 4.3. Горение смеси газов” я рассказала о гипотетических (предполагаемых) алгоритмических приемах для 28 задания ЕГЭ и подробно описала первую фишку:
1) Расчеты по уравнениям реакции горения смеси газов, состав которой нужно определить предварительно
2) Определение объемного состав смеси по участникам процесса горения (задачи на уравнения с двумя неизвестными)
3) Определение состава смеси газообразных продуктов, если в условии избыток-недостаток, степень превращения или выход реакции
4) Задачи на изменение объема газовой смеси в процессе реакции
Сегодня речь пойдет о второй предполагаемой фишке “Определение объемного состав смеси по участникам процесса горения (задачи на уравнения с двумя неизвестными)”. Мое мнение – это абсолютно простые задачи. Самое сложное в них – решить систему уравнений с двумя неизвестными. Итак, поехали!
Задание 28*(1)
Для сжигания 20 л смеси пропана и бутана израсходовано 124 л кислорода. Определить объемный состав смеси.
Решаем задачу с применением Четырех Заповедей (шагов). Каждое выполненное действие обводится зеленым овалом.
1. Первая Заповедь. Выписать данные задачи в разделе “Дано”.
2. Вторая заповедь. Написать уравнение реакции.
В задаче протекает две реакции. При написании реакций, не забываем делать отступ над каждой – для дальнейших расчетов.
3. Третья заповедь. Сделать предварительные расчеты
Выписываем два досье – на пропан и бутан. В каждом досье прописываем объем газа. Пугаться не нужно, если мы не знаем значение объема. Что нам математика говорит? “Если не знаешь число – пиши неизвестное (Х или Y). Советую в каждое досье записать также объем кислорода, который был израсходован на сжигание газа. Для это выполняются стандартные расчеты по уравнению реакций. Как это сделать? Очень просто! Читайте мою статью: “Команда “Газы!” дана для всех! 4.1 Закон Гей-Люссака. Закон Авогадро. Горение” и
Составляем два алгебраических уравнения. Одно – по сумме объемов газов (20 л), второе – по общему объему кислорода, затраченного на сжигание (124 л). Решение системы уравнений лучше проводить методом сложения-вычитания (меньше действий, значит, меньше вероятность технической ошибки). В ответе мы получим объемы каждого газа.
4. Четвертая заповедь. Составить алгоритм решения задачи.
Алгоритм решения составляем по вопросу задачи: “Определить объемный состав смеси” Объемный состав смеси газов – это значения объемных долей каждого газа, которые определяют по формуле, описанной в статье “Вангую новую фишку в заданиях ЕГЭ по химии”
Решим еще парочку задач на закрепление алгоритма.
Задание 28*(2)
Для сжигания 10 л метан-пропановой смеси израсходовано 205 л воздуха. Определить объемный состав исходной смеси.
Задача решается аналогично предыдущей, только вначале следует “извлечь” кислород из 205 л воздуха. Кстати, мы должны помнить объемную долю кислорода в воздухе – 20% (более точно 21%).
Задание 28*(3)
2,8 л смеси СО и СО2 прореагировали с 0,56 г кислорода. Определить объемный состав исходной смеси.
Из двух газов в смеси, только один участвует в реакции горения – угарный газ. Его объем рассчитывают по уравнению реакции через объем кислорода. А вот объем кислорода рассчитывают по его массе, используя универсальную расчетную единицу – количество вещества (моль). Состав смеси хорошо виден в таблице. Кстати, делать расчеты по таблице очень удобно и я советую использовать такой технический прием для ускорения решения задач и визуализации алгоритма.
Задание 28*(4)
При сжигании 350 л смеси метана и ацетилена в кислороде получили 775 л смеси СО2 и кислорода с плотностью по воздуху 1,424. Вычислите объемный состав исходной смеси.
Достаточно своеобразная задача. Поэтому разберу ее подробно, по Четырем Заповедям.
1) Первая Заповедь. Выписать данные задачи в разделе “Дано”
2) Вторая Заповедь. Написать уравнения реакции
3. Третья Заповедь. Сделать предварительные расчеты по данным условия задачи и по уравнению реакции.
Небольшой стоп! Я предупредила, задача необычная – нужно найти состав смеси реагентов по составу смеси продуктов. Поэтому, первые предварительные расчеты – определить состав смеси продуктов по средней молярной массе. Этот прием я подробно описывала в статье статье “Вангую новую фишку в заданиях ЕГЭ по химии”.
После определения объемных долей газов-продуктов, определяем объем углекислого газа – это суммарный углекислый газ, который выделился и при сжигании метана, и при сжигании ацетилена.
Применяем уже известный нам алгоритм – “Определение объемного состав смеси по участникам процесса горения (задачи на уравнения с двумя неизвестными)”. На этапе предварительных расчетов определяем объемы газов-реагентов
4. Четвертая заповедь. Составить алгоритм решения задачи. Алгоритм решения составляется по вопросу задачи: “Вычислите объемный состав исходной смеси”. Объемный состав исходной смеси рассчитывается по формуле объемной доли (объем каждого газа делится на общий объем смеси). Эту и другие формулы я подробно разобрала в вышеуказанной статье “Вангую новую фишку в заданиях ЕГЭ по химии”
Вот и все. Задача решена. Усидчивым читателям – респект и уважуха 👍! Если еще остались силы, можете попробовать решить задачи самостоятельно, не подсматривая в мое объяснение. Если сил уже нет, идите пить чай с имбирем, шоколадом и горячими плюшками ☕️ 🍫 🥧 (рецепт отличных плюшек прочитаете в следующих статьях). И до скорого свидания на полях Яндекс Дзен!
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии http://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Звоните мне +7(903) 186-74-55. Приходите ко мне на курс, на Мастер-классы “Решение задач по химии” – и вы сдадите ЕГЭ с высочайшими баллами, и станете студентом престижного ВУЗа!
PS! Если вы не можете со мной связаться из-за большого количества звонков от моих читателей, пишите мне в личку ВКонтакте, или на Facebook. Я обязательно отвечу вам.
Репетитор по химии и биологии кбн В.Богунова
Смесям идеальных газов характерно свойство аддитивности двух показателей: парциального давления и объёма. Другими словами, любому включённому в смесь инертному газу характерно такое поведение, какое было бы, если б он в единственном числе заполнял предлагаемый объём. Для лучшего понимания разумно разобраться, что выражают указанные величины.
Определения
Давление – действующая на единицу поверхности сила, прямопропорциональная числу и скоростью сталкивающихся с этой поверхностью молекул, зависящей от температуры.
Парциальное давление – давление, оказываемое компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя этот объём и текущую температуру.
Объём – ограниченное чертой трёхмерное пространство, вмещающее вещество и отображающее его форму.
Парциальный объём – объём, занимаемый компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя первоначальное давление и температуру.
Идеальный газ – научная модель для познания газов, не учитывающая силу молекулярного взаимодействия.
Смесь идеальных газов – это совокупность газов, каждый из которого, находясь в смеси, при сохранении заданных условий, не вступает в химическую реакцию с остальными компонентами.
Говоря об идеальных газах и их смеси, следует понимать, что изменение условий, например температуры или давления, всё же может спровоцировать химическую реакцию. Важным параметром такой смеси является молярная (весовая) концентрация газового компонента. Данная величина измеряется в мг/м3 и показывает количество конкретного компонента в единице объёма газовой смеси.
Парциальное давление
Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальное давление, создаваемое i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем pi.
Формула
Формула парционального давления:
[p i=frac{m_{i}}{mu_{i}} frac{R T}{V}=mu_{i} frac{R T}{V}]
Где V– объём смеси, R = 8,31
Дж/моль*K– универсальная газовая постоянная, а T –
температура.
Следует отметить, что равность средней кинетической энергии находящихся в смеси молекул определяет равенство температур всех компонентов термодинамически уравновешенной газовой смеси. Найти общее давление смеси идеальных газов представляется возможным через закон Дальтона, отражаемый аддитивность парциальных давлений, а именно [p=sum p_{i}].
Пользуясь данным законом, найдём давление смеси идеальных газов через следующую формулировку: [p=sum_{i}^{N}=1 rightarrow p_{i}=frac{R T}{V} sum_{i}^{N}=1^{v_{i}}], где N – количество вошедших в смесь газов, vi– количественный показатель молей i-го газа. Отсюда парциальное давление можно выразить формулой [p_{i}=x_{i} p], где xi – молярная концентрация i-го газа.
Понятие парциального объёма
Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальный объём, занимаемый i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем Vi. Аддитивность парциального объёма определяет закон Амага, выраженный формулой [V=sum_{i}^{N}=1 V_{i}].
Формула
Пользуясь данным законом, можно вывести формулу нахождения парциального объёма через следующую формулировку:
[v_{i}=frac{p^{V_{i}}}{R T}]; [p=frac{R T}{V} frac{p}{R T} sum_{i}^{N}=mathbf{1}^{V}_{i}] , отсюда
следует, что — [boldsymbol{V=sum_{i}^{N}=1^{V_{i}}}, text{ а } boldsymbol{V_{i}=x_{i} V}].
Зная, что характеризующие состояние смеси инертных газов показатели подчиняются уравнению Менделеева-Клапейрона, выведем формулу:
[p V=frac{m}{mu_{s m}} R T] данное уравнение свои параметры относит ко всей газовой смеси.
[pV=mR_{s m} T] такой вариант уравнения содержит показатель Rsm, обозначающий удельную газовую составляющую смеси.
Уравнение Менделеева-Клапейрона показывает возможность изменения трёх характеризующих состояние идеального газа параметров.
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления парциального давления и объёма
Задача №1
Условие: в сосуде объёмом 2 м3, при постоянной температуре 290 К находится 0,20*10-3 кг гелия и 1*10-3 кг водорода. Необходимо вычислить давление смеси и парциальное давление гелия.
Решение.
Сначала вычислим количество молей каждого компонента, используя следующую формулу:
[mathrm{v}{mathrm{i}}=frac{mathrm{m}{mathrm{i}}}{mu_{mathrm{i}}}]
Для расчёта количество молей водорода в смеси нам понадобится его молярная масса, которую возьмём из таблицы Менделеева:
[mu_{mathrm{H}_{2}}=2 * 10^{-3} frac{mathrm{кг}}{text { моль }}]
Теперь можно найти количество молей водорода в смеси:
[mathrm{v}_{mathrm{H}_{2}}=frac{mathrm{m}_{mathrm{H}_{2}}}{mu_{mathrm{H}_{2}}}=frac{1 * 10^{-3}}{2 * 10^{-3}}=0,5 text { (моль) }]
Зная молярную массу гелия из таблицы Менделеева, рассчитаем количество молей гелия в смеси:
[mathrm{v}_{mathrm{He}}=frac{mathrm{m}_{mathrm{He}}}{mu_{mathrm{He}}}=frac{4 * 10^{-3}}{20 * 10^{-3}}=0,2 text { (моль) }]
Теперь можно найти парциальное давление каждого из компонентов с помощью уравнения Менделеева-Клапейрона:
[mathrm{p}_{mathrm{i}} mathrm{V}=mathrm{v}_{mathrm{i}} mathrm{RT}]
Сначала нужно рассчитать давление водорода:
[mathrm{p}_{mathrm{H}_{2}} mathrm{~V}=mathrm{v}_{mathrm{H}_{2}} mathrm{RT} rightarrow mathrm{p}_{mathrm{H}_{2}}=frac{mathrm{v}_{mathrm{H}_{2}} mathrm{RT}}{mathrm{V}}=frac{0,5 * 8,31 * 290}{1}=1205 text { (Па) }]
Рассчитаем парциальное давление гелия:
[mathrm{p}_{mathrm{He}}=frac{mathrm{v}_{mathrm{He}} mathrm{RT}}{mathrm{V}}=frac{0,2 * 8,31 * 290}{1}=482 text { (Па) }]
Теперь найдём полное давление газовой смеси, сложив значения компонентов:
[mathrm{p}=mathrm{p}_{mathrm{H}_{2+}} mathrm{p}_{mathrm{H}}=1205+482=1687 text { Па }]
Ответ: парциальное давление гелия равно 482 Па, а общее давление 1205 Па.
Задача №2
Условие: идеальная газовая смесь состоит из 0,5 кг углекислого газа и 0,25 кг кислорода, какой объём они займут, если давление равно 1 атм, а температура смеси равна 300 К?
Решение.
Найдём суммарную массу газовой смеси:
[mathrm{m}=mathrm{m}_{mathrm{O}_{2}}+mathrm{m}_{mathrm{CO}_{2}}=0,5+0,25=0,75 text { (кг) }]
Вычислим массовые компоненты смеси:
[g_{mathrm{O}_{2}}=frac{0,25}{0,75}=0,33] [mathrm{g}_{mathrm{CO}_{2}}=frac{0,5}{0,75}=0,67]
Тогда газовая постоянная смеси равняется:
[mathrm{R}_{mathrm{sm}}=mathrm{R} sum_{mathrm{i}=1}^{mathrm{N}} frac{mathrm{g}_{mathrm{i}}}{mu_{mathrm{i}}}=8,31left(frac{0,33}{32 * 10^{-3}}+frac{0,67}{46 * 10^{-3}}right)=200left(frac{text { Дж }}{text { кгК }}right)]
Пользуясь уравнением Менделеева-Клапейрона, и, зная, что 1 атм равна 105 Па,вычислим объём смеси:
[mathrm{V}_{mathrm{sm}}=frac{mathrm{m}_{mathrm{sm}} mathrm{R}_{mathrm{sm}} mathrm{T}_{mathrm{sm}}}{mathrm{P}_{mathrm{sm}}}=frac{0,75 * 200 * 300}{10^{5}}=0,45left(mathrm{м}^{3}right)]
Ответ: при заданных условиях смесь займёт 0,45 м3.
Навык определения парциальных давлений и объёма актуален в машиностроении, энергетике и других промышленностях, связанных с использованием тепловых двигателей, приводимых в действие парами высокой температуры.
“Только из союза двоих, работающих
вместе и при помощи друг друга, рождаются великие
вещи.”
Антуан Де Сент-Экзюпери
Математика многообразна и многогранна.
Существует ряд ситуаций в образовательном
процессе, когда при изучении какой-либо темы по
физике, химии, биологии и т.д. затрагиваются
понятия математики, например, существуют задачи,
которые решают как на уроках математики, так и на
уроках химии. Способы решения задач представляют
и учителя химии, и математики, но есть проблема:
математики знают математику, а химики – химию. И
не всегда способы совпадают.
В данной статье приводятся рекомендации по
решению химических задач на смешение растворов
разными способами: с помощью расчетной формулы,
“Правила смешения”, “Правила креста”,
графического метода, алгебраического метода.
Приведены примеры решения задач.
1. Основные химические понятия
Приведем некоторые указания к решению задач на
растворы.
Основными компонентами этого типа задач
являются:
а) массовая доля растворенного вещества в
растворе;
б) масса растворенного вещества в растворе;
в) масса раствора.
Предполагают, что:
а) все получившиеся смеси и сплавы являются
однородными;
б) смешивание различных растворов происходит
мгновенно;
в) объем смеси равен сумме объемов смешиваемых
растворов;
г) объемы растворов и массы сплавов не могут
быть отрицательными.
Определения и обозначения.
Массовая доля растворенного вещества в
растворе – это отношение массы этого вещества к
массе раствора.
![]()
где ![]() – массовая
– массовая
доля растворенного вещества в растворе;
![]() – масса
– масса
растворенного вещества в растворе;
![]() – масса
– масса
раствора.
Следствия формулы (1):
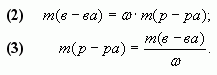
Введем обозначения:
![]() – массовая доля
– массовая доля
растворенного вещества в первом растворе;
![]() –
–
массовая доля растворенного вещества во втором
растворе;
![]() –
–
массовая доля растворенного вещества в новом
растворе, полученном при смешивании первого и
второго растворов;
m1(в-ва), m2(в-ва), m(в-ва) – массы
растворенных веществ в соответствующих
растворах;
m1(р-ра), m2(р-ра), m(р-ра) – массы
соответствующих растворов.
Основными методами решения задач на смешивание
растворов являются: с помощью расчетной формулы,
“Правило смешения”, “Правило креста”,
графический метод, алгебраический метод.
Приведем описание указанных методов.
1.1. С помощью расчетной формулы
В наших обозначениях, получим формулу для
вычисления массовой доли вещества (?) в смеси.
1. Масса полученного при смешивании раствора
равна:
m(р-ра) = m1(р-ра) + m2(р-ра).
2. Определим массы растворенных веществ в
первом и втором растворах:
m1(в-ва)= ![]() •m1(р-ра), m2(в-ва)=
•m1(р-ра), m2(в-ва)= ![]() •m2(р-ра).
•m2(р-ра).
3. Следовательно, масса растворенного вещества
в полученном растворе вычисляется как сумма масс
веществ в исходных растворах:
m(в-ва) = m1(в-ва) + m2(в-ва) = ![]() •m1(р-ра) +
•m1(р-ра) + ![]() •m2(р-ра).
•m2(р-ра).
4. Таким образом, массовая доля растворенного
вещества в полученном растворе равна:
![]()
или
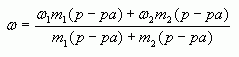
или
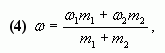
где ![]() – массы
– массы
соответствующих растворов.
Замечание: При решении задач удобно
составлять следующую таблицу.
|
1-й раствор |
2-й раствор |
Смесь двух растворов |
|
|
Масса растворов |
m1 |
m2 |
m1 + m2 |
|
Массовая доля |
|
|
|
|
Масса вещества в |
|
|
|
1.2. “Правило смешения”
Воспользуемся формулой (4): ![]()
тогда 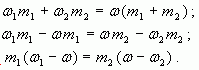
Отсюда ![]()
Таким образом, отношение массы первого
раствора к массе второго равно отношению
разности массовых долей смеси и второго раствора
к разности массовых долей первого раствора и
смеси.
Аналогично получаем, что при ![]()
Замечание: Формула (5) удобна тем, что на
практике, как правило, массы веществ не
отвешиваются, а берутся в определенном
отношении.
1.3. “Правило креста”
“Правилом креста” называют диагональную
схему правила смешения для случаев с двумя
растворами.
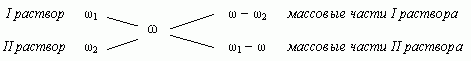
Слева на концах отрезков записывают исходные
массовые доли растворов (обычно слева
вверху-большая), на пересечении отрезков –
заданная, а справа на их концах записываются
разности между исходными и заданной массовыми
долями. Получаемые массовые части показывают в
каком отношении надо слить исходные растворы.
1.4. Графический метод
Отрезок прямой (основание графика)
представляет собой массу смеси, а на осях ординат
откладывают точки, соответствующие массовым
долям растворенного вещества в исходных
растворах. Соединив прямой точки на осях ординат,
получают прямую, которая отображает
функциональную зависимость массовой доли
растворенного вещества в смеси от массы
смешанных растворов в обратной пропорциональной
зависимости 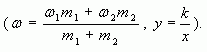
Полученная функциональная прямая позволяет
решать задачи по определению массы смешанных
растворов и обратные, по массе смешанных
растворов находить массовую долю полученной
смеси.
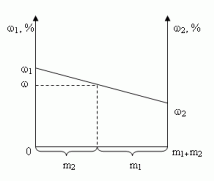
Построим график зависимости массовой доли
растворенного вещества от массы смешанных
растворов. На одной из осей ординат откладывают
точку, соответствующую массовой доли ![]() , а на другой –
, а на другой – ![]() . Обозначим на оси абсцисс
. Обозначим на оси абсцисс
точки А и В с координатами (0,0) и (m1 + m2,0),
соответственно. На графике точка А(0,0)
показывает, что массовая доля всего раствора
равна ![]() , а точка В(m1
, а точка В(m1
+ m2,0) – массовая доля всего раствора равна ![]() . В направлении от
. В направлении от
точки А к точке В возрастает содержание в
смеси 2-го раствора от 0 до m1+ m2 и
убывает содержание 1-го раствора от m1+ m2
до 0. Таким образом, любая точка на отрезке АВ будет
представлять собой смесь, имеющую одну и ту же
массу с определенным содержанием каждого
раствора, которое влияет на массовую долю
растворенного вещества в смеси.
Замечание: Данный способ является наглядным
и дает приближенное решение. При использовании
миллиметровой бумаги можно получить достаточно
точный ответ.
1.5. Алгебраический метод
Задачи на смешивание растворов решают с
помощью составления уравнения или системы
уравнений.
2. Примеры решения задач
Задача 1. (№1.43, [1])
В 100 г 20%-ного раствора соли добавили 300 г её
10%-ного раствора. Определите процентную
концентрацию раствора.
Решение:
- C помощью расчетной формулы
- Графический
- Путем последовательных вычислений
- Сколько растворенного вещества содержится:
- Сколько вещества содержится в образовавшемся
растворе? - Чему равна масса образовавшегося раствора?
- Какова процентная концентрация полученного
раствора? - Алгебраический

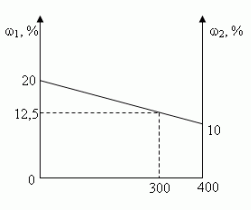
Ответ: 12,5%
а) в 100 г 20%-ного раствора; [100•0,2 = 20(г)]
б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)]
20 г + 30 г = 50 г
100 г + 300 г = 400 г
(50/400)100 = 12,5(%)
Ответ: 12,5%
Пусть х – процентная концентрация
полученного раствора. В первом растворе
содержится 0,2•100(г) соли, а во втором 0,1•300(г), а в
полученном растворе х•(100 + 300)(г) соли.
Составим уравнение:
0,2•100 + 0,1•300 = х•(100 + 300);
х = 0,125 (12,5%)
Ответ: 12,5%
Задача 2. u(№10.26, [1])
Смешали 10%-ный и 25%-ный растворы соли и получили 3
кг 20%-ного раствора. Какое количество каждого
раствора в килограммах было использовано?
Решение:
- Алгебраический
- Графический.
- “Правило смешения”
- “Правило креста”
а) C помощью уравнения:
Пусть х (кг) – масса 1-го раствора, тогда 3-х (кг)
-масса 2-го раствора.
0,1•х (кг) содержится соли в 1-ом растворе,
0,25•(3-х) (кг) содержится соли в 2-ом растворе,
0,2•3 (кг) содержится соли в смеси.
Учитывая, что масса соли в 1-ом и 2-ом растворах
равна массе соли в смеси, составим и решим
уравнение:
0,1•х + 0,25•(3-х) = 0,2•3;
0,15х = 0,15;
х = 1, 1кг-масса 1-го раствора
3 – х = 3 – 1 =2 (кг) – масса 2-го раствора.
Ответ: 1 кг, 2 кг.
б) С помощью системы уравнений
Пусть х (кг) – количество первого раствора, у (кг)
– количество второго раствора. Система уравнений
имеет вид:
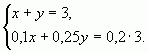
Ответ: 1 кг, 2 кг.
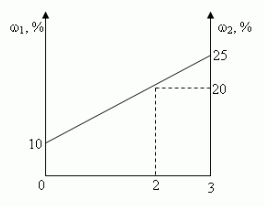
Ответ: 1кг, 2кг.

Составим диагональную схему
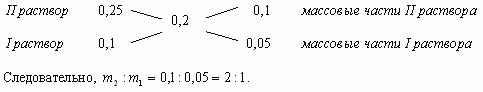
Ответ: 1кг, 2кг.
Задача 3 ([2])
Сосуд емкостью 5 л содержит 2 л р%-ного (по объёму)
раствора соли. Сколько литров 20%-ного раствора
такой же соли надо налить в сосуд, чтобы
процентное содержание соли в сосуде стало
наибольшим?
Решение (графический способ)
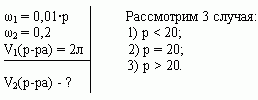
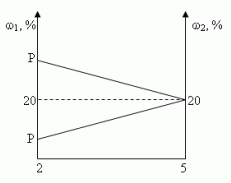
Заметим, что по условию, объём второго раствора
не превышает трёх литров.
- Ели р < 20, то для того, чтобы получить
максимальную массовую долю вещества в растворе,
необходимо добавить 3 л 20% – ного раствора соли; - Если р = 20, то при добавлении 2-го раствора,
процентное содержание соли в растворе не
изменится, следовательно, можно прилить от 0 л до 3
л 20% – ного раствора соли; - Если р > 20, то при добавлении 2-го раствора,
процентное содержание соли будет уменьшаться,
т.е. прилить нужно 0 л.
Ответ: 3 л, если 0 < р < 20, [0,3], если р = 20, 0л, если 20
< р ![]() 100.
100.
Задача 4 (работа 5, №2, [1])
В двух сосудах по 5л каждый содержится раствор
соли. Первый сосуд содержит 3л р% – ного раствора, а
второй – 4л 2р% – ного раствора одной и той же соли.
Сколько литров надо перелить из второго сосуда в
первый, чтобы получить в нем 10% – ный раствор соли?
При каких значениях р задача имеет решение?
Решение
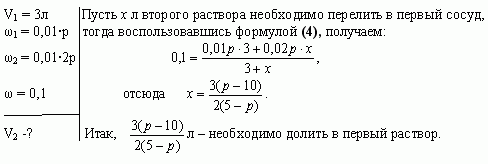
Найдем, при каких значениях р задача имеет
решение. По условию задачи 5-ти литровый сосуд
содержит 3л первого раствора, следовательно, к
нему можно прилить от 0 до 2л второго раствора.
Имеем, ![]() Решая
Решая
неравенство, получаем ![]()
Ответ: ![]()
3. Заключение
Данные рекомендации предназначены учителям
математики, желающим организовать элективные
курсы, как в девятых, так и в десятых и
одиннадцатых классах. Цель создаваемых курсов:
научить учащихся пользоваться математическим
аппаратом при решении химических задач.
Список литературы
- Галицкий и др. Сборник задач по алгебре для 8-9
классов: Учебное пособие для учащихся шк. и
классов с углубл. изуч. математики / М.Л. Галицкий,
А.М. Гольдман, Л.И. Звавич.-2-е изд. – М.:
Просвещение,1994. – 271с. - Сборник задач по математике для поступающих в
вузы: Учебное пособие/ П.Т.Дыбов, А.И.Забоев, А.С.
Иванов и др.; Под ред. А.И. Прилепко. – М.:Высш. школа,
1983. – 239 с. - Ерыгин Д.П., Шишкин Е.А. Методика решения задач по
химии: Учебное пособие для студентов пед. ин-тов
по биол. и хим. спец. – М.: Просвещение,1989. – 176с. - Хомченко Г.П., Хомченко И.Г. Задачи по химии для
поступающих в вузы: Учебное пособие. – 2-е изд..
исправ. и доп. – М.: Высш. школа, 1993. – 302 с.
Смесь, состоящая из
двух и более компонентов, характеризуется
свойствами и содержанием этих компонентов.
Состав смеси может быть задан массой,
объемом, количеством (числом молей или
килограмм-молей) отдельных компонентов,
а также значениями их концентраций.
Концентрацию компонента в смеси можно
выразить в весовых, мольных и объемных
долях или процентах, а также в других
единицах.
Массовая
доля i
какого-либо компонента определяется
отношением массы mi
данного компонента к массе всей смеси
mсм:
![]()
![]()
![]()
Учитывая,
что суммарная масса смеси равна сумме
масс отдельных компонентов, т.е.
![]()
можно написать:
![]()
или сокращенно:
![]()
Пример
4. Смесь
состоит из двух компонентов: m1
= 500 кг, m2
= 1500 кг. Определить массовую долю каждого
компонента в смеси.
Решение.
Массовая
доля первого компонента:
![]()
mсм=
m1
+ m2
= 500 + 1500 = 2000 кг
Массовая доля второго компонента:
![]()
Массовую
долю второго компонента можно определить
также, используя равенство:
1
+ 2
= 1
2
= 1 – 1
= 1 – 0,25 = 0,75
Объемная
доля i
компонента в смеси равна отношению
объема Vi
данного компонента к объему всей смеси
V:
![]()
![]()
![]()
Учитывая, что:
![]()
можно написать:
![]()
Пример
5.
Газ состоит из двух компонентов: V1
= 15,2 м3
метана и V2
= 9,8 м3
этана. Подсчитать объемный состав смеси.
Решение.
Общий объем смеси равен:
V
= V1
+ V2
= 15,2 + 9,8 = 25 м3
Объемная доля в смеси:
метана
![]()
этана
v2
= 1 – v1
= 1 – 0,60 = 0,40
Мольная
доля ni
какого-либо компонента смеси определяется
как отношение числа киломолей Ni
данного компонента к общему числу
киломолей N
смеси:
![]()
![]()
![]()
Учитывая,
что:![]()
получим:![]()
Пересчет мольных
долей в массовые можно проводить по
формуле:
![]()
Пример
6. Смесь
состоит из 500 кг бензола и 250 кг толуола.
Определить мольный состав смеси.
Решение.
Молекулярный
вес бензола (С6Н6)
равен 78, толуола (С7Н8)
– 92. Число килограмм-молей равно:
бензола
![]()
толуола
![]()
общее число
килограмм-молей:
N
= N1
+ N2
= 6,41 + 2,72 = 9,13
Мольная доля
бензола равна:
![]()
Для толуола мольная
доля может быть найдена из равенства:
n1
+ n2
= 1
откуда: n2= 1 –n1= 1 – 0,70 = 0,30
Среднюю молекулярную
массу смеси можно определить, зная
мольную долю и молекулярную массу
каждого компонента смеси:
![]() (21)
(21)
где
ni
— содержание
компонентов в смеси, мол. доли; Mi
— молекулярная
масса компонента смеси.
Молекулярную массу смеси нескольких
нефтяных фракций можно определить по
формуле
 (22)
(22)
или
![]() (23)
(23)
где
m1,
m2,…,
mn
— масса
компонентов смеси, кг; M1,
М2,….,.Мп
– молекулярная масса компонентов смеси;
![]() – % масс. компонента.
– % масс. компонента.
Молекулярную
массу нефтепродукта можно определить
также по формуле Крэга
 (24)
(24)
Пример
7.
Определить среднюю молекулярную массу
смеси бензола с изооктаном, если мольная
доля бензола составляет 0,51, изооктана
0,49.
Решение.
Молекулярная масса бензола 78, изооктана
114. Подставляя эти значения в формулу
(21), получаем
Мср
= 0,51
78 + 0,48114
= 95,7
Пример
8. Смесь
состоит из 1500кг бензола и 2500кг н-октана.
Определить среднюю молекулярную массу
смеси.
Решение.
Используем формулу (22)

Объемный
молярный состав пересчитывают в массовый
следующим образом. Данный объемный
(молярный) состав в процентах принимают
за 100 молей. Тогда концентрация каждого
компонента в процентах будет выражать
число его молей. Затем число молей
каждого компонента умножают на его
молекулярную массу и получают массу
каждого компонента в смеси. Разделив
массу каждого компонента на общую массу,
получают его массовую концентрацию.
Массовый
состав пересчитывают в объемный
(молярный) следующим образом. Принимают,
что смеси взято 100 (г, кг, т) (если массовый
состав выражен в процентах), массу
каждого компонента делят на его
молекулярную массу. Получают число
молей. Делением числа молей каждого
компонента на их общее число получают
объемные (молярные) концентрации каждого
компонента.
Средняя плотность
газа определяется по формуле:
![]() кг/м3;
кг/м3;
г/см3
или, исходя из
объемного состава:
![]() ,
,
или, исходя из
массового состава смеси:
 .
.
Относительную плотность определяют по
формуле:
![]()
Пример 9.Пересчитать массовый
состав газа в объемный и определить его
молекулярную массу, его плотность и
относительную плотность.
|
Компоненты |
М г/моль |
массовый % масс. |
mi |
Число
|
Объемный |
|
|
доли единицы |
% об. |
|||||
|
Метан |
16 |
40 |
40 |
40:16=2,50 |
0,669 |
66,9 |
|
Этан |
30 |
10 |
10 |
10:30=0,33 |
0,088 |
8,8 |
|
Пропан |
44 |
15 |
15 |
15:44=0,34 |
0,091 |
9,1 |
|
Бутан |
58 |
25 |
25 |
25:58=0,43 |
0,115 |
11,5 |
|
Пентан + высшие |
72 |
10 |
10 |
10:72=0,14 |
0,037 |
3,7 |
|
100 |
100 |
3,74 |
1,000 |
100,0 |
Для
простоты расчета примем массу смеси за
100 г, тогда масса каждого компонента
будет численно совпадать с процентным
составом. Найдем число молей ni
каждого компонента. Для этого массу
каждого компонента mi
разделим на мольную массу:
![]()
Находим объемный
состав смеси в долях единицы
i(CH4)
= 2,50 : 3,74 = 0,669;
![]() (C2H6)
(C2H6)
= 0,33 : 3,74 = 0,088;
![]()
![]() (C5H8)
(C5H8)
= 0,34 : 3,74 = 0,091;
![]() (C4H10)
(C4H10)
= 0,43 : 3,74 = 0,115;
![]()
![]() (C5H12)
(C5H12)
= 0,14 : 3,74 = 0,037.
Находим
объемный состав смеси в процентах,
умножив данные в долях единицы на 100%.
Все полученные данные заносим в таблицу.
Рассчитываем
среднюю массу смеси.
![]()
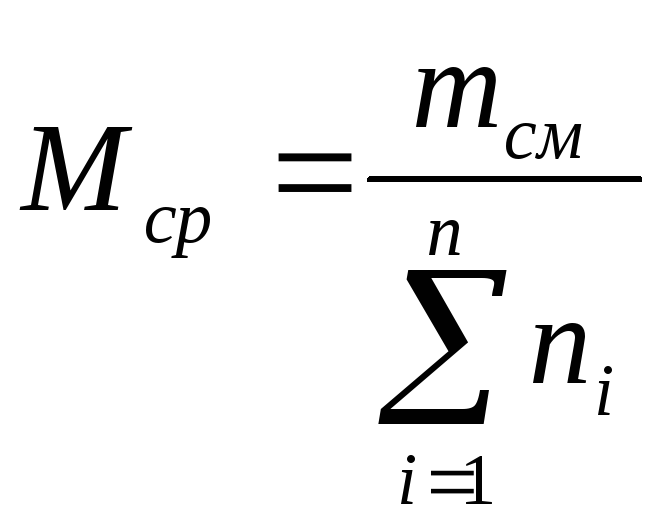
Мср
= 100 : 3,74 =
26,8 г/моль
Находим
плотность смеси
![]()
Находим относительную
плотность:
![]()
Пример 10.Пересчитать объемный
состав в массовый и определить его
молекулярную массу, его плотность и
относительную плотность.
|
Компоненты |
М г/моль |
Объемный % об. |
число |
Масса г. |
Весовой |
|
|
доли единицы |
% масс. |
|||||
|
Метан |
16 |
30 |
30 |
3016=480 |
0,117 |
11,7 |
|
Этан |
30 |
15 |
15 |
15·30=450 |
0,109 |
10,9 |
|
Пропан |
44 |
20 |
20 |
20·44=880 |
0,214 |
21,4 |
|
Бутан |
58 |
15 |
15 |
15·58=870 |
0,211 |
21,1 |
|
Пентан + высшие |
72 |
20 |
20 |
20·72=1440 |
0,349 |
34,9 |
|
100 |
100 |
4120 |
1,000 |
100,0 |
![]() (CH4)
(CH4)
= 480 : 4120 = 0,117;
![]() (C2H6)
(C2H6)
= 450 : 4120 = 0,109;
![]()
![]() (C3H8)
(C3H8)
= 880 : 4120 = 0,214;
![]() (C4H10)
(C4H10)
= 870 : 4120 = 0,211;
![]()
![]() (C5H12)
(C5H12)
= 1440 : 4120 = 0,349.
Мср
= 4120 : 100 =
41,2 г/моль.
![]() г/л
г/л
![]()
![]()
Задача 15. Смесь состоит из пяти
компонентов. Определить массовую,
объемную и мольную долю каждого компонента
в смеси, среднюю молекулярную массу
смеси.
|
Компоненты смеси |
Вариант |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
mi |
mi |
mi |
||||||||
|
метан |
5 |
30 |
55 |
80 |
100 |
75 |
50 |
25 |
5 |
30 |
|
этан |
10 |
35 |
60 |
85 |
95 |
70 |
45 |
20 |
10 |
35 |
|
пропан |
15 |
40 |
65 |
90 |
90 |
65 |
40 |
15 |
15 |
40 |
|
н-бутан |
20 |
45 |
70 |
95 |
85 |
60 |
35 |
10 |
20 |
45 |
|
изобутан |
25 |
50 |
75 |
100 |
80 |
55 |
30 |
5 |
25 |
50 |
Задача 16.Пересчитать массовый
состав газа в объемный и определить его
молекулярную массу, плотность и
относительную плотность по воздуху.
|
Компоненты смеси |
ω% массовый |
|||||||||
|
Варианты |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
метан |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
этан |
50 |
45 |
40 |
35 |
30 |
25 |
20 |
15 |
10 |
5 |
|
пропан |
5 |
10 |
20 |
10 |
5 |
10 |
15 |
20 |
25 |
30 |
|
бутан |
10 |
10 |
20 |
15 |
30 |
25 |
20 |
15 |
10 |
5 |
|
пентан |
30 |
25 |
5 |
20 |
10 |
20 |
10 |
10 |
10 |
10 |
Задача 17. Пересчитать объемный
состав газа в массовый и определить его
молекулярную массу, плотность и
относительную плотность по воздуху.
|
Компоненты смеси |
объемный состав |
|||||||||
|
Варианты |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
метан |
10 |
5 |
20 |
5 |
20 |
10 |
10 |
35 |
40 |
10 |
|
этан |
45 |
50 |
15 |
20 |
25 |
30 |
10 |
20 |
15 |
5 |
|
пропан |
10 |
5 |
10 |
20 |
10 |
5 |
25 |
15 |
20 |
30 |
|
бутан |
10 |
10 |
35 |
40 |
25 |
30 |
10 |
20 |
15 |
5 |
|
пентан |
15 |
30 |
20 |
15 |
30 |
25 |
45 |
10 |
10 |
50 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #

