Способы амортизации в налоговом учете: вам просто или быстро?
Оглавление
- 1 Что будем амортизировать
- 2 Линейный способ начисления амортизации
- 3 Нелинейный метод начисления амортизации
- 4 Как рассчитать суммарный баланс группы
- 5 Ликвидация группы и выбытие объектов

Налоговый кодекс дает на выбор разные способы амортизации в налоговом учете. Какой лучше выбрать и как определить сумму амортизации за месяц?
Что будем амортизировать
Сначала определимся, по каким основным средствам мы имеем право начислять амортизацию в налоговом учете. В НК используется такое понятие, как амортизируемое имущество. Под ним понимают имущество, которым организация владеет на праве собственности, оно используется для получения дохода, срок службы имущества больше 12 месяцев, а первоначальная стоимость более 40 000 рублей. Как видно из определения, в отличие от бухгалтерского учета здесь установлен лимит стоимости основных средств.
Однако есть такое имущество, которое отвечает требованиям, но амортизируемым имуществом все-таки не считается (п.2 ст.256 НК):
— объекты природопользования, в том числе земельные участки;
-имущество бюджетных учреждений и некоммерческих организаций;
— имуществу, купленному за счет бюджетных средств целевого финансирования;
— произведения искусства, приобретенные здания, объекты внешнего благоустройства.
Есть также ситуации, когда имущество исключается из амортизируемого имущества (п.3 ст.256 НК):
— передача в безвозмездное пользование по договору;
— на консервации более 3 мес.;
— на реконструкции и модернизации более 12 мес.
Линейный способ начисления амортизации
Установлены такие способы амортизации в налоговом учете: линейный и нелинейный. Линейный, по сути, совпадает с таковым методом из бухгалтерского учета. Однако есть и отличие: в бухучете сначала считают сумму за год, а потом делят на 12, а в налоговом учете считают для месяца.
В линейном способе амортизация считается за каждый месяц (п.1 ст.259 НК):
А = ПС * НА
ПС – первоначальная (восстановительная стоимость);
НА – норма амортизации.
НА = 1 / n * 100%
n – срок полезного использования в месяцах.
Расчет суммы амортизации ведется отдельно для каждого объекта, а потом все величины суммируются.
Пример: ООО «Океан» приобрело оборудование для переработки рыбы. Установлен срок полезного использования 120 месяцев (о том, как определить срок использования, смотрите тут). Первоначальная стоимость 480 000 руб.
Норма амортизации: 1/120 * 100% = 0,83%
Ежемесячная сумма амортизации: 480 000 руб. *0,83% = 4000 руб.
Нелинейный метод начисления амортизации
В отличие от линейного метода в нелинейном амортизация считается не по отдельным объектам, а по всем основным средствам, входящим в группу. Для расчета за месяц используется такая формула:
А = В * (k / 100)
В – суммарный баланс группы на начало месяца;
k – норма амортизации для группы.
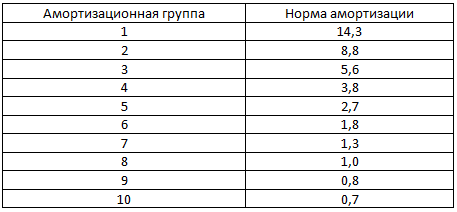
Нормы амортизации не рассчитываются, они уже есть готовые в Налоговом кодексе (п.5 ст.259.2).
Пример:
ООО «Зима» работает с января 2012 года, использует нелинейный метод начисления амортизации. 15 января приобретен компьютер за 45000 руб. (без НДС), срок полезного использования – 25 месяцев (вторая амортизационная группа). Амортизацию начнем начислять с февраля:
45000 * (8,8% / 100%) = 3960 руб.
Пусть в феврале приобретен еще один такой же компьютер. Суммарный баланс на 1 марта составит: 45 000 – 3960 + 45 000 = 86 040 руб.
а амортизация за март:
(45 000 – 3960 + 45 000) * (8,8% / 100%) = 7571,52 руб.
Способы амортизации в налоговом учете выбираются налогоплательщиком самостоятельно. Исключение: для зданий, сооружений, передаточных устройств, которые включены в 8-10 группу, можно использовать только линейный метод. Способ начисления амортизации можно менять, но не чаще раза в 5 лет и только с начала года.
Как рассчитать суммарный баланс группы
Норму амортизации мы установили, для каждой группы она будет своя. Теперь посмотрим, как рассчитать суммарный баланс по группе.
Суммарный баланс нужно рассчитывать как общую (суммарную) остаточную стоимость всех объектов, которые отнесены к отдельной группе или подгруппе. Если вы переходите с линейного на нелинейный метод, то определите суммарный баланс на 1 января года, с которого вы решили применять нелинейный метод.
Далее суммарный баланс групп рассчитывается на 1-е число месяца, для которого считают амортизацию. Суммарный баланс – величина переменная, он может как уменьшаться, так и увеличиваться:
— выбытие объектов или ввод новых в эксплуатацию;
— изменение первоначальной стоимости объектов в результате модернизации, реконструкции и т.д.
-каждый месяц баланс уменьшается на суммы начисленной амортизации.
Ликвидация группы и выбытие объектов
Амортизационная группа должна быть ликвидирована:
— если имущество выбывает из группы и баланс группы становится нулевым;
— суммарный баланс группы становится меньше 40 тыс. руб. на первые числа двух месяцев подряд.
Если объект выбывает из амортизационной группы до окончания его срока полезного использования, то нужно «извлечь» его остаточную стоимость. Для этого используется формула:
Sn = S * (1 – 0,01 * k)n
где: Sn – остаточная стоимость объектов после того как прошло n месяцев с момента включения основных средств в данную амортизационную группу (подгруппу);
S – первоначальная (или же восстановительная) стоимость объектов основных средств;
k – норма амортизации (если есть повышающий коэффициент, то он тоже учитывается), установленная для данной амортизационной группы (подгруппы);
n – количество полных месяцев, которые прошли со дня включения основных средств в амортизационную группу (подгруппу) до дня исключения их из состава данной группы (подгруппы), не считая полных месяцев, в которых основные средства не были в составе амортизируемого имущества. Важно: если объект выбывает из состава группы в последний день месяца, то этот месяц не участвует в расчетах остаточной стоимости.
Когда закончился срок полезного использования объекта, его исключают из состава группы без изменения суммарного баланса группы.
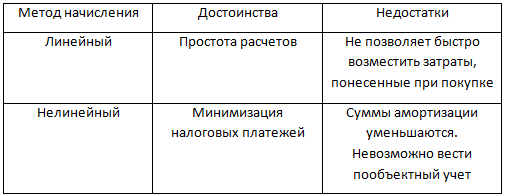
Следует отметить, что и линейный, и нелинейный методы начисления амортизации в налоговом учете имеют свои достоинства и недостатки, которые приведены в таблице.
Какие методы начисления амортизации можно использовать в бухгалтерском учете, смотрите здесь . А как правильно определить срок полезного использования объекта, читайте тут .
Какой метод используете вы? Как думаете, сложно ли использовать на практике более выгодный – нелинейный метод? Поделитесь, пожалуйста, в комментариях!
Бывает, он сопряжен с некоторыми неудобствами, но это лучше, чем ничего.
Приветствую Вас, уважаемые Читатели! Сегодня хочу немного погрузиться в теорию делимости, а именно в вычисление остатков от деления. Эта задача является и практически важной, ведь такие операции применяются буквально повсюду: от криптографии до телекоммуникационных систем. Поехали!
Итак, начнем с определения:
Так же такие числа называются сравнимыми по модулю m.
Для равноостаточных чисел работает такая теорема:
- Если при делении на m числа a1,a2,a3… an соответственно равноостаточны числам b1,b2.b3…bn, то равноостаточными будут суммы a1+a2+a3+…+an и b1+b2+b3+…bn, а также произведения a1a2a3…an и b1b2b3…bn.
- Как следствие, если числа a и b равноостаточны, то такими же являются и числа a^n и b^n при любо натуральном n.
Формулировка весь запутанная, поэтому разберем два пример. Итак:
Теперь пример посложнее с многоступенчатым решением:
В итоге мы получаем хоть и меньшее, но всё равно трудно вычисляемое вручную число, поэтому продолжаем дальше:
На третьем шаге уже нет смысла вычислять все остатки, как прежде. Можно было и вычислить вручную. Получаем, что первоначальное число и число 56 равноостаточны при делении на 37. Ответ получен! Спасибо за внимание!
Читайте также:
Слово имеет итальянское происхождение, его перевод звучит примерно, как «расчет» или «остаток». С XIX века понятие начали применять в отношении остатков по счетам бухучета. Принципиально смысловая нагрузка слова не изменилась и приобрела довесок – употребление и в переносном смысле, использование в описании внешнеэкономической деятельности. Задавая вопрос, сальдо что это такое простыми словами, мы рассчитываем услышать нечто необычное. Однако истоки термин не потерял и поныне ассоциируется в первую очередь с бухучетом.
Выбрать кредит для бизнеса
Что такое сальдо простыми словами
Сальдо – это разность значений дебета и кредита счетов. В самом общем из значений сальдо предполагает некий остаток на определенный день, разницу. На видах сальдо мы остановимся чуть позже, а сейчас рассмотрим примеры значений этого слова в разных сферах.
Во внешней торговле – это разность между страновым экспортом и импортом. С помощью анализа платежного баланса можно анализировать плавающие курсы валют РФ и определять давление на курс национальной валюты.
В платежах – разность между оплаченными и полученными от контрагентов суммами. В квитанциях на оплату услуг ЖКХ – это остаток (то есть переплата с предыдущего месяца) по лицевому счёту квартиры.
Что такое сальдо в бухгалтерии простыми словами
Как уже говорилось выше, для бухучёта данное понятие носит едва ли не сакральное значение. Отражая разность между дебетом и кредитом счетов, сальдо может быть и на левой, и на правой стороне счёта. Напомним, что правая сторона – это кредит, показывающий поступления на счет, когда он пассивный и расход, когда счет активный. Левая сторона – это дебет, где наоборот, поступления отображаются, когда счет активный, а расход, когда счет пассивный.
При каждом движении сумм по счету разница между правой или левой стороной изменяется. Изменяется, таким образом, сальдо счета.
Рассмотрим простейший пример просчета сальдо в бухгалтерском учете счета в таблице ниже.
|
ДЕБЕТ |
КРЕДИТ |
||
|
Сальдо начальное по дебету |
10 000 руб. РФ |
||
|
Продажа 10.12.2023 |
5000 руб. РФ |
||
|
Продажа 20.12.2023 |
1000 руб. РФ |
||
|
Покупка 22.12.2023 |
3 000 руб. РФ. |
||
|
Оборот по дебету |
3 000 руб. РФ |
Оборот по кредиту |
6 000 руб. РФ |
|
Сальдо на конец периода |
7 000 руб. РФ |
Предположим у нас есть фирма, по счету которой рассматривается движение сырья. Такой счет будет активным (сырьё – это ресурс, актив), поэтому на начало месяца мы имеем сальдо по дебету – сырья в наличии на 10 000 руб. РФ. По ходу месяца сырье продавалось (на 5 и на 1 тыс. руб. РФ соответственно), а значит и списывалось со счета. Покупка шла в актив по дебету на 3 тыс. руб. РФ.
К окончанию учетного периода, суммировав обороты по дебету и кредиту, вычисляем конечное сальдо дебетовое (на конец месяца) – 10 000 + 3 000 – 6 000 = 7 000 руб. РФ. Эта сумма также является ответом на вопрос: что означает сальдо счёта?
Если сальдо равно нулю, то такой счет принято называть закрытым.
Виды сальдо, их характеристика
Выше мы так или иначе затрагивали большинство видов сальдо, но в данном разделе мы предлагаем более подробное и структурированное их описание.
- Дебетовое сальдо – состояние счета, отражаемое по дебету. Характерная черта данного состояния – дебет превышает кредит. Данное сальдо отображает состояние активов организации на требуемую дату.
- Кредитовое сальдо – некоторое состояние счета. Специфичной его чертой является факт превышения кредитом дебита. Состояние пассивов (они же источники средств) отображает кредитовое сальдо.
- Активное сальдо имеет место, когда стоимостная оценка средств, полученных организацией, выше ее расходной части.
- Пассивное сальдо – ситуация с точностью до наоборот. Образуется, когда расходы выше активной части.
- Начальное сальдо – сальдо на начало периода, результат хозяйственной деятельности организации за предыдущий период времени (начало нынешнего является концом предыдущего).
- Конечное сальдо. Его также называют исходящим – результат движений по счёту на конец временного промежутка.
- Сальдо за отрезок времени – результирующее операций за некоторый период.
- Сальдо баланса торговли – термин из сферы экономической теории – подразумевается разность между стоимостью экспортируемых и импортируемых товаров и услуг за некоторый промежуток времени.
- Сальдо платёжного баланса – экономический термин, который показывает разницу между суммами заграничных денежных платежей и суммами, проследовавшими в противоположном направлении – в страну.
Обнаружили ошибку? Выделите ее и нажмите Ctrl + Enter.
Оцените страницу:
Уточните, почему:
не нашёл то, что искал
содержание не соответствует заголовку
информация сложно подана
другая причина
Расскажите, что вам не понравилось на странице:
Спасибо за отзыв, вы помогаете нам развиваться!
Онлайн калькулятор определит остаток от деления чисел, поможет проверить себя при решении уроков и примеров на деление. Деление с остатком (деление по модулю) — это арифметическая операция, в результате выполнения которой получается два целых числа: неполное частное и остаток от деления.
Остаток всегда должен быть меньше делителя. Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Подсчет остатка от деления большого числа
Для проверки на всякие чек-суммы, иногда нужно делить что-то вроде 6796573475894375894375893479583745897943759830 на какой-нибудь 73 или 97.
Далеко не все языки программирования на это рассчитаны. Есть, конечно и примочки в виде классов типа BigInt и т.п., но есть способ похитрее.
(A*B) mod N = ((A mod N) * (B mod N)) mod N
(A+B) mod N = ((A mod N) + (B mod N)) mod N
Другими словами, есть представить число 43517 как 7 + 10 + 500 + 3000 + 40000, т.е. 7*10^-1 + 1 * 10^1 + 5 * 10^2 + 3 * 10^3 + 4 * 10^4, то многое упрощается.
Остаток от деления цифры это легко, а если делитель больше 9, то и вовсе равняется самой цифре.
Что же касается степеней десятки, то тут, кажется, ничего не изменилось, ведь все равно нужно посчитать остаток от деления 10000000000000000000000000000 на 73.
Ан нет! Мы знаем, что 10^2 это 10*10, 10^3 это 10*10^2, а 10^N это 10*10^(N-1),
Из этого и нашей формулы следует, что (10^N) mod M = ((10^(N-1) mod M) * 10) mod M.
Таким образом, можно этот остаток вычислять итеративно, на каждом шаге, начиная с младшей цифры и до старшей, каждый раз берем остаток из предыдущего шага, умножаем на 10 и вычисляем остаток.
Вот так можно его и посчитать.
Пример.
Остаток от деления 1275436137 на 97.
Вначале, напишем наши цифры 7 3 1 6 3 4 5 7 2 1.
Посчитаем остатки от деления степеней 10-ки на 97. (При программировании, если делитель встречается часто, лучше всего эти результаты закешировать для более быстрых расчетов, подгружая массив в память, когда это нужно.)
1 mod 97 — 1, без вопросов.
(1 * 10) mod 97 — 10
(10 * 10) mod 97 — 3
(3 * 10) mod 97 — 30
(30 * 10) mod 97 — 9
(9 * 10) mod 97 — 90
(90 * 10) mod 97 — 27
(27 * 10) mod 97 — 76. и дальше 81, 34.
Перемножаем пары, складываем. У нас все цифры имеют ровно такие же остатки, так что
7 * 1 + 3 * 10 + 1 * 3 + 6 * 30 + 3 * 9 + 4 * 90 + 5 * 27 + 7 * 76 + 2 * 81 + 1 * 34 = 1470
1470 mod 97 = 15
Ответ. 1275436137 mod 97 = 15, что можно проверить на виндошном калькуляторе.
В псевдокоде
s <- 0
a <- 1
for i = LastDigitIndex to 1
s <- s + a * digits[i]
a <- (a * 10) mod n
endfor
result <- s mod n
Остаток от деления числа в большой степени
Как можно быстро вычислить (x^n)mod y. Уже когда-то копал этот вопрос и обнаружил теорему Эйлера (теория чисел).
Не относится к вопросу: Но вся проблема в том, что я учусь в школе, и мы не проходили еще подобных выражений, найденных мною на wiki, и теории чисел. Объясните пожалуйста:
- Как использовать эту теорему на практике(например, реализация на C).
- (Не так важно, но просто интересно)Кратко значение формулировки на
wiki. Буду рад какой-нибудь статье, etc для тех, кто еще не знаком с теорией чисел и математикой >9 классов.
Наприклад ми хочемо обчислити 7 222 (mod 10). Маємо, що 7 і 10 є взаємно простими і φ(10) = 4 . Одже згідно з теоремою Ейлера 7 4 ≡ 1 (mod 10) і як наслідок
7 222 ≡ 7 4×55 + 2 ≡ (7 4 ) 55 x 7 2 ≡ 1 55 x 7 2 ≡ 49 ≡ 9 (mod 10).
Моя попытка перевода:
Например мы хотим вычислить “7 222 (mod 10)”. 7 и 10 являются взаимно-простыми и φ(10) = 4 (это число натуральных чисел не больших чем 10 и являющихся взаимнопростыми по отношению к 10 . Это следующие числа: 1,3,7,9 и всего их 4 ).
Следовательно согласно теореме Эйлера 7 4 ≡ 1 (mod 10) и как следствие:
7 222 ≡ 7 4×55 + 2 ≡ (7 4 ) 55 x 7 2 ≡ 1 55 x 7 2 ≡ 49 ≡ 9 (mod 10).
Следствия из теоремы:
если a φ(n) ≡ 1 (mod n), то и (a φ(n) ) k ≡ 1 (mod n) для любого положительного k , т.к.
(a φ(n) ) k ≡ a φ(n) mod n * (a φ(n) ) k — 1 mod n ≡ (a φ(n) ) k — 1 (mod n) и т.д.
Остаток от деления больших чисел
числа по модулю образуют кольцо (а по простому — даже поле), то есть — нормальную арифметику. Модуль можно брать на любом этапе.
конечно, посчитать сначала 18^180, а потом взять (mod 13) — это долго (хотя на компе вполне реально, до нескольких миллионов знаков длинная арифметика считается несложно). Но можно брать модуль на каждом шаге!
например, 18^180 mod 13 = (18mod 13)^180 mod 13=5^180 mod 13.
теперь, как возводить в высокую степень (не обязательно по мудулю):
a^180=a^(4+16+32+128)
считаем и запоминаем промежуточные результаты
a^2=a*a
a^4=(a^2)(a^2)
a^8=(a^4)(a^4)
a^16=(a^4)(a^4)
a^32=(a^16)(a^16)
a^64=(a^32)(a^32)
a^128=(a^64)(a^64)
итого a^180=a^4 * a^16 * a^32 * a^128
если надо считать по модулю 13 — делаем каждую операцию по модулю 13, все числа — небольшие, не больше 12.
если немного подумать, то разложение a^180=a^(4+16+32+128) — это просто двоичное представление числа, 4,16,32,128 — единички, остальные — нули.