Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.
Задачи урока:
- формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля; - научить учащихся применять формулу E=kq/r2 в решении
несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности
электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями; - между зарядами нигде не прерываются.
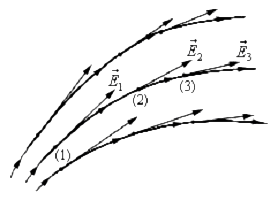
Рис.1
Силовые линии положительного заряда:
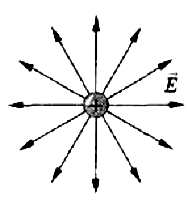
Рис.2
Силовые линии отрицательного заряда:
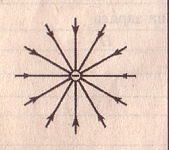
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
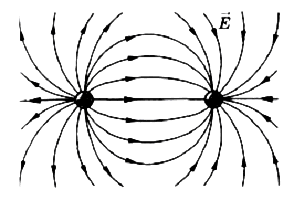
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
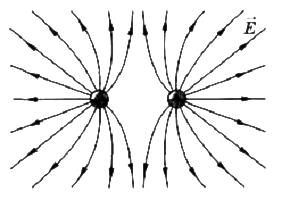
Рис.5
Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
![]() или
или
![]() .
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда
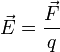
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда
![]()
где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.
В системе СИ
![]() Н·м2/Кл2,
Н·м2/Кл2,
где ε0 – электрическая
постоянная, равная 8,85·10-12 Кл2/Н·м2;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:
![]()
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
Е = kq1/x2 + kq2/(r – x)2
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
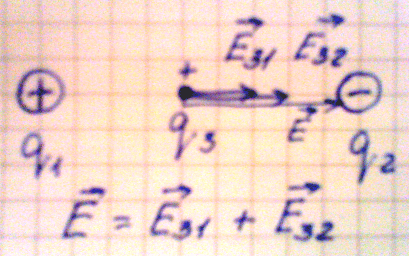
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a)2 – kq2/a2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
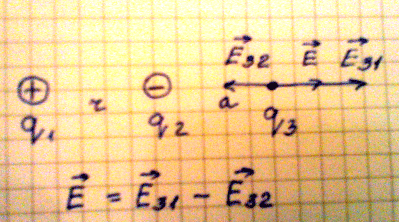
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
Е = (Е312 +Е322)1/2
Следовательно:
Е = ((kq1/r2 )2 + (kq2/b2)2)1/2
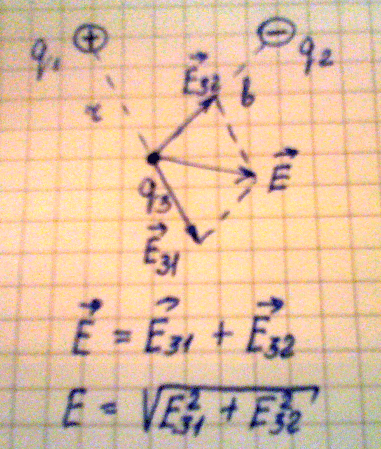
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
Проверочная работа.
Вариант № 1.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Вариант № 2.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Задачи на дом:
1. Два заряда q1 = +3·10-7 Кл и q2 = −2·10-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10-9 Кл действует сила 3·10-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.
Методика
решения задач на нахождение напряжённости
результирующего поля аналогична методике
нахождения результирующей силы,
действующей на точечный заряд со стороны
других точечных зарядов (см. раздел
1.1), только вместо закона Кулона
используется формула напряженности
точечного заряда (2.2).
 .
.
Задача
2.1. Два
точечных заряда q1
и q2
находятся на расстоянии d
друг от друга. Найти напряжённость в
точках А, В, С и D
(рис. 13). Считаем расстояния от зарядов
q1
и q2
до заданных точек известными и во всех
случаях обозначаем r1
и r2
соответственно.
Р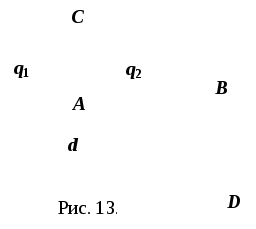 ешение.
ешение.
Сделаем рисунок для каждого случая
отдельно. Так как заряды оба отрицательные,
то векторы напряжённостей
![]() и
и![]() направлены в каждом случае к зарядамq1
направлены в каждом случае к зарядамq1
и q2
вдоль линии, соединяющей заряд и заданную
точку, и берут начало в заданной точке.
Направление
результирующего вектора
![]() определяетсяпо
определяетсяпо
принципу суперпозиции
путём векторного сложения. Поэтому
векторная запись для всех случаев
одинакова:
![]() .
.
Модуль
(длина) каждого из векторов рассчитывается
по формуле напряженности точечного
заряда (2.2). Модуль результирующего
вектора определяется из геометрических
построений.
-
В
точке А (рис. 14, а) векторы
 и
и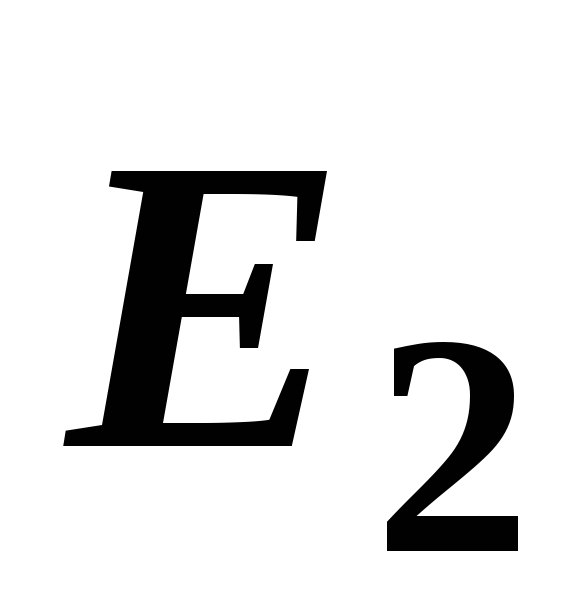 направлены в противоположные стороны,
направлены в противоположные стороны,
поэтому модуль результирующего вектора определяется как разность модулей
определяется как разность модулей
векторов и
и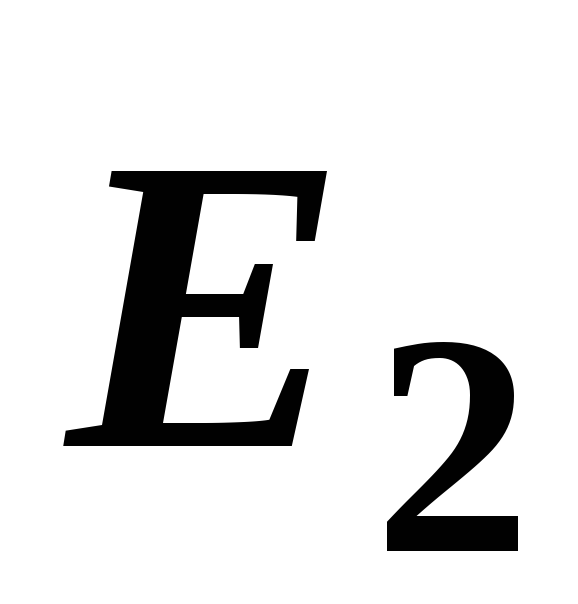 и направлен в сторону большего вектора:
и направлен в сторону большего вектора:
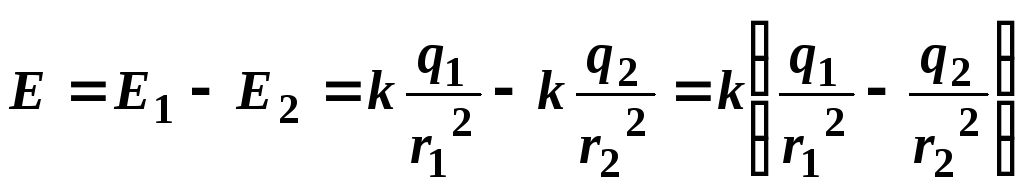 .
.
-
В
точке В (рис. 14, б) векторы
 и
и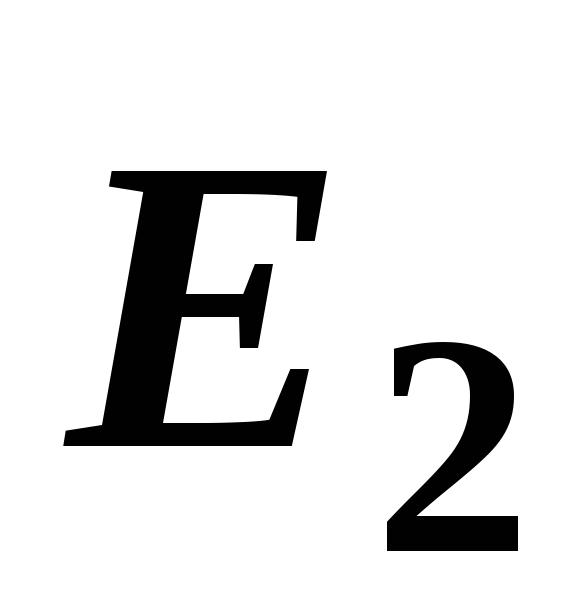 направлены в одну сторону, поэтому
направлены в одну сторону, поэтому
модуль результирующего вектора определяется
определяется
как сумма модулей векторов и
и и направлен в эту же сторону:
и направлен в эту же сторону:
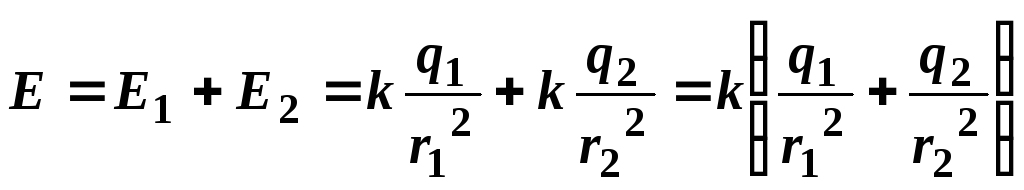 .
.
-
В
 точке С (рис. 14, в) векторы
точке С (рис. 14, в) векторы и
и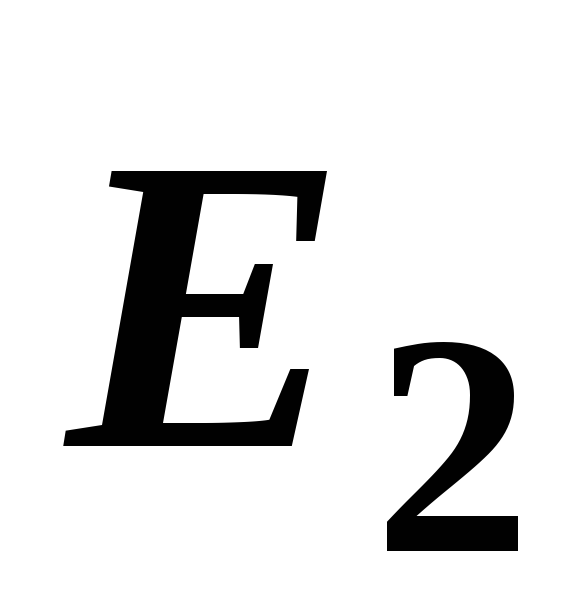 взаимно перпендикулярны, поэтому модуль
взаимно перпендикулярны, поэтому модуль
результирующего вектора является гипотенузой прямоугольного
является гипотенузой прямоугольного
треугольника и определяется по теореме
Пифагора:
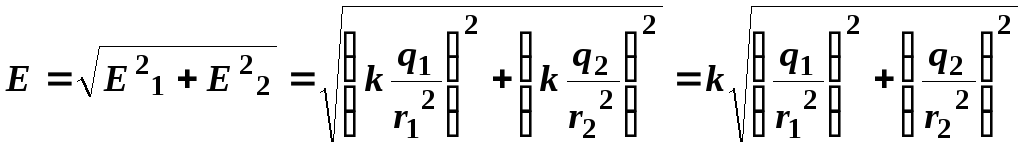 .
.
-
В
точке D
(рис. 14, г) векторы
 и
и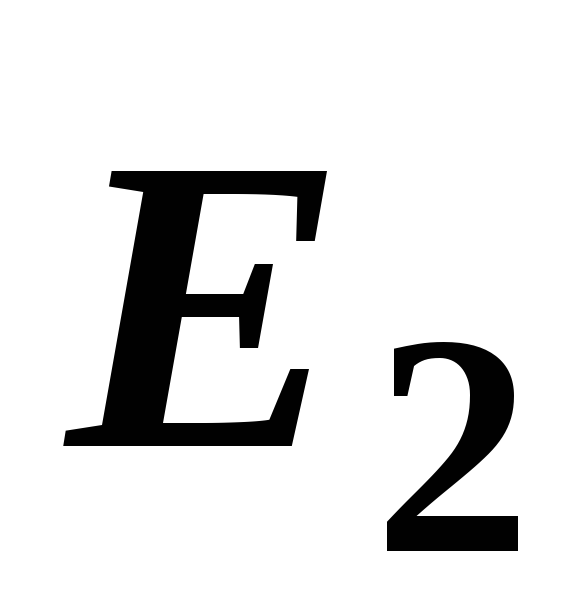 образуют треугольник, поэтому модуль
образуют треугольник, поэтому модуль
результирующего вектора определяется
определяется
по теореме косинусов:
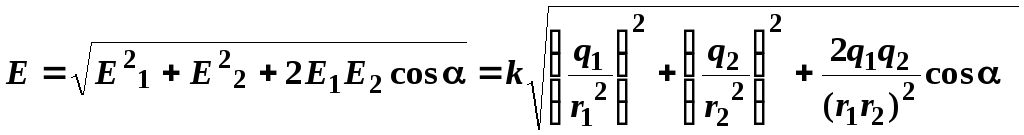 .
.
Если
угол α
неизвестен, то его определяют, используя
теорему косинусов для треугольника со
сторонами r1,
r2,
d:
![]() .
.
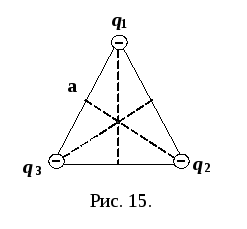
Задача
2.2. Поле
создано тремя одинаковыми точечными
зарядами q,
расположенными в вершинах равностороннего
треугольника со стороной а.
Вычислить напряжённость электростатического
поля в точке, находящейся на пересечении
высот этого треугольника.
Решение.
Так как напряжённость электростатического
поля
![]() – величина
– величина
векторная, то необходимо определить
направление этого вектора и его модуль
(длину).
Направление
вектора напряжённости результирующего
поля определяем с помощью принципа
суперпозиции:
![]() ,
,
где
![]() ,
,![]() и
и![]() – напряжённость электростатического
– напряжённость электростатического
поля, созданного каждым зарядом в
отдельности.
-
С
 начала
начала
строим векторы ,
,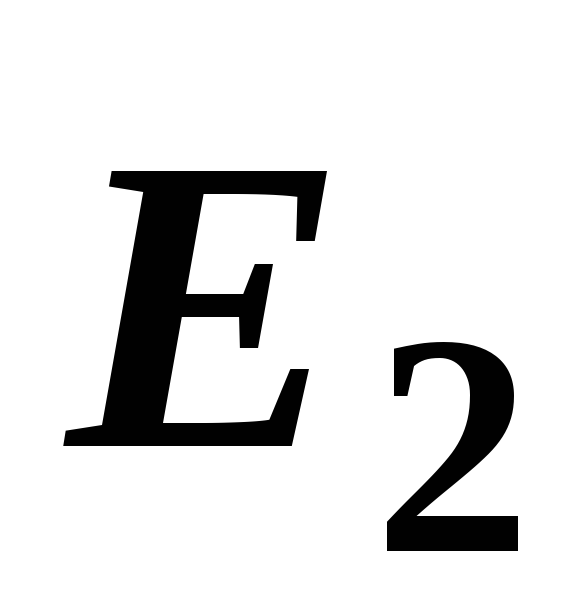 и
и ,
,
берущиеначало
в заданной точке. Так как все заряды
одинаковые, а заданная точка равноудалена
от них, то длины этих векторов будут
равны. Поскольку знак зарядов
отрицательный, то векторы
 ,
,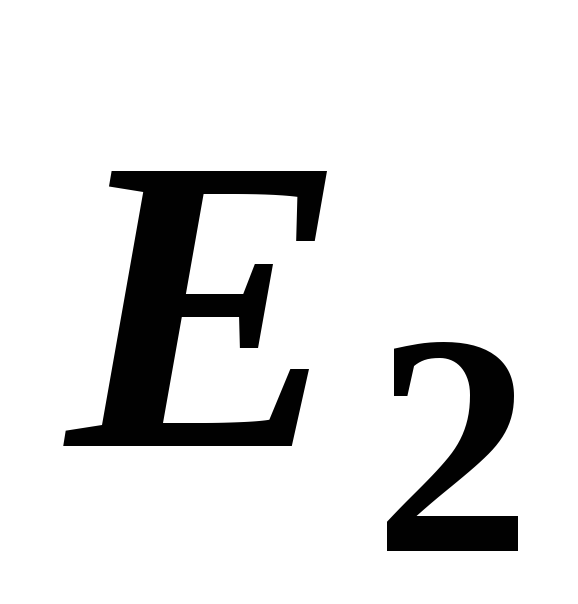 и
и будут направлены к зарядам (рис. 15).
будут направлены к зарядам (рис. 15). -
Складываем
геометрически векторы
 и
и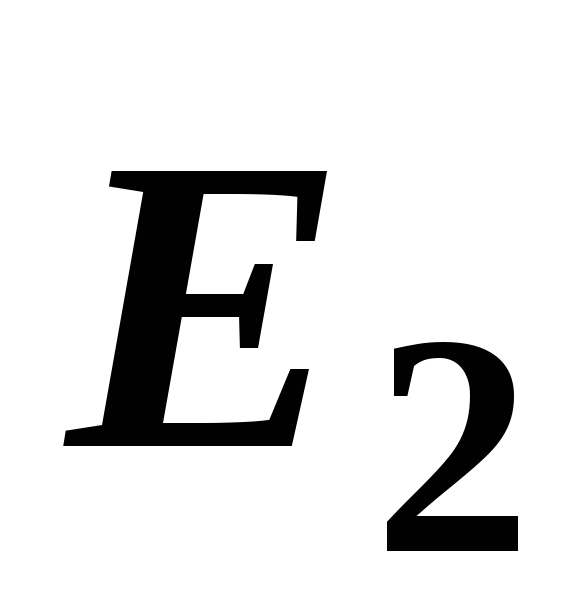 .
.
Результирующий вектор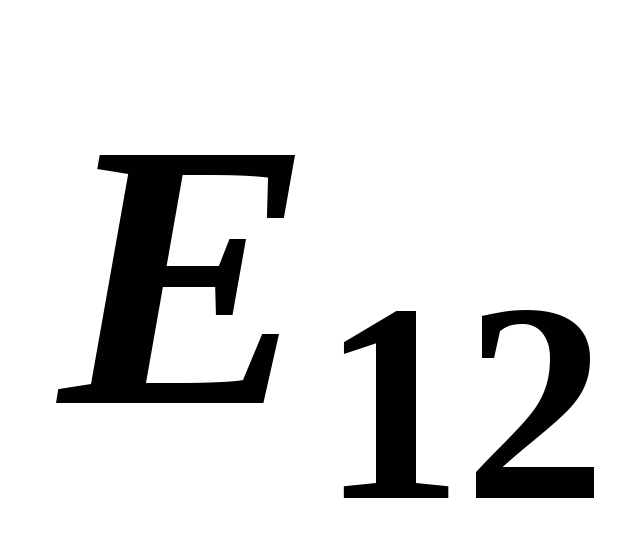 будет лежать на той же прямой, что и
будет лежать на той же прямой, что и
вектор .
. -
Находим
длину вектора
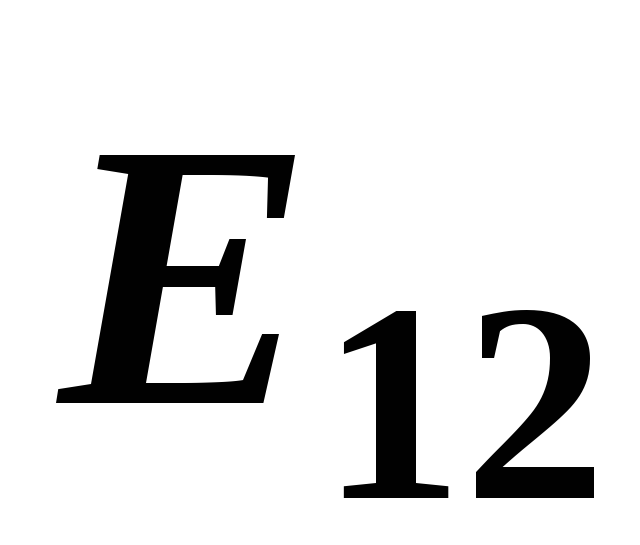 по теореме косинусов:
по теореме косинусов:
![]() ,
,
где
α
– угол между векторами
![]() и
и![]() .
.
С
учётом того, что Е1
= Е2,
α = 120º, cos 120º
= – 0,5, получим:
![]() .
.
-
Складываем
геометрически векторы
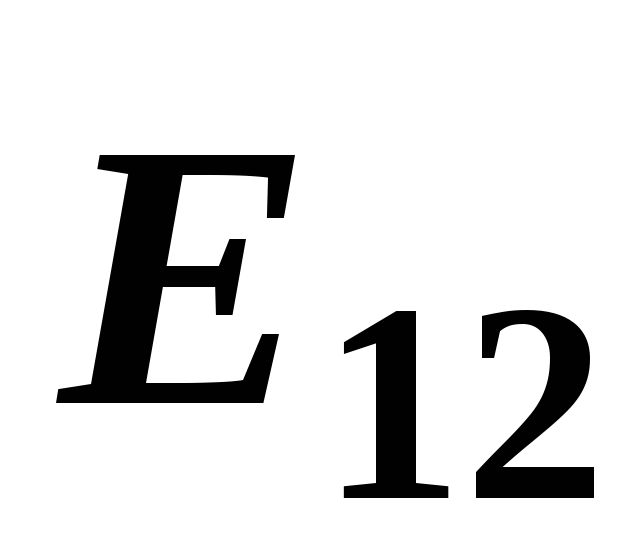 и
и .Так
.Так
как эти векторы равны по длине и
противоположны по направлению, то их
векторная сумма равна нулю:
![]() .
.
Методика
расчета не меняется, если образующие
систему заряды имеют другие знаки и
расположения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вектор суммарного электрического поля
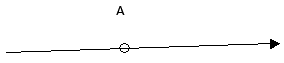
Задание 13. Два неподвижных точечных электрических заряда -q и +q (q> 0) расположены, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости суммарного электрического поля этих зарядов в точке А? Ответ запишите словом (словами).

Известно, что вектор напряженности электрического поля исходит из положительного заряда и входит в отрицательный заряд. Поэтому, в точке A мы увидим примерно следующую картину направления векторов напряженности электрического поля (см. синие стрелки на рисунке ниже).

Из рисунка видно, что вектор напряженности направлен вправо к отрицательному заряду.
Вектор напряженности электрического поля
По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.
Характеристика электрического поля
Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:
E → = F → q , где F → – сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.
У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.
Силовые линии
Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.
Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
E → = ∑ i = 1 n E → i .
Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:
Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l – линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.
Интегрирование по объему выполняется, если имеется объемное распределение заряда:
ρ = d q d V , где ρ – объемная плотность распределения заряда.
Что называется напряженностью электрического поля
Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:
Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:
E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.
Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равняется:
E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .
В системе СГС напряженность поля точечного заряда в вакууме:
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.
Решение
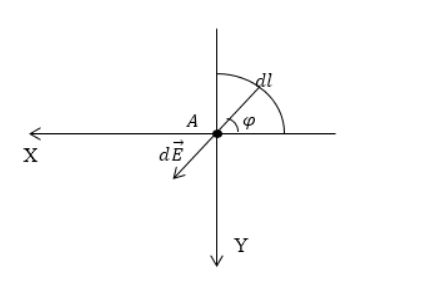
Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:
d E → = d q R 3 R → R .
Проекция вектора d E → на ось О х составит:
d E x = d E cos φ = d q cos φ R 2 .
Произведем выражение d q через линейную плотность заряда τ :
d q = τ d l = τ · 2 πRdR .
Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :
d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
где 2 π d R = d φ .
Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
по d φ с изменением угла 0 ≤ φ ≤ 2 π .
E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .
Перейдем к проекции вектора напряженности на О у :
d E y = d E sin φ = τ R sin φ d φ .
Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :
E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = – τ R cos φ π 2 0 = – τ R .
Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:
E = E x 2 + E y 2 = τ R 2 + – τ R 2 = τ R 2 .
Ответ: E = τ R 2 .
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .
Решение
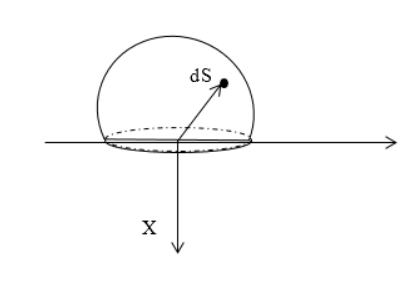
Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:
d S = R 2 sin θ d θ d φ ,
при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .
Элементарная напряженность поля точечного заряда в системе С И :
d E → = d q 4 π ε 0 R 3 R → R .
Необходимо спроецировать вектор напряженности на О х :
d E x = d q cos θ 4 π ε 0 R 2 .
Произведем выражение заряда через поверхностную плотность заряда:
Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:
E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .
Отсюда следует, что E = E x .
Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .
Вектор суммарного электрического поля
На рисунке представлено расположение двух неподвижных точечных электрических зарядов и
Направлению вектора напряженности электрического поля этих зарядов в точке A соответствует стрелка
По принципу суперпозиции, напряженность поля в точке A есть сумма напряженностей полей, создаваемых зарядами и по отдельности. Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом, — от заряда. Таким образом, напряженности полей зарядов направлены в точке A в разные стороны. Поле точечного заряда ослабевает с расстоянием как заряды по величине одинаковые, поэтому поле от отрицательного заряда в точке A сильнее, чем поле от положительного заряда. Следовательно, направлению напряженности электрического поля в точке A соответствует стрелка 2.
Если мы помещаем отрицательный заряд в точку А, то не будут ли они отталкиваться с ближайшим (-q). Не понимаю, почему ответ не 4
Отрицательный заряд будет, конечно, будет отталкиваться. Но за направление вектора напряженности выбирается направление силы, действующей со стороны электрического поля на положительный заряд.
На рисунке показано расположение двух неподвижных точечных электрических зарядов и В какой из трех точек — А, B или C — модуль вектора напряженности суммарного электрического поля этих зарядов максимален?
4) во всех трех точках модуль напряженности поля имеет одинаковые значени
Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом, — от заряда. Следовательно, в точках A и C поля направлены в разные стороны, а в точке B сонаправлены. Поле точечного заряда по модулю пропорционально величине заряда и обратно пропорционально квадрату расстояния до него: Таким образом, модуль вектора напряженности суммарного электрического поля этих зарядов максимален в точке B.
Т. е. точки A, B, C – пробные заряды?
Пробные (малые заряды) нужны для экспериментального исследования “сложных” электрических полей, создаваемых нетривиальными (неточечными) распределениями заряда.
Если изучается поле, создаваемое конечным числом точечных зарядов, нужды в пробных зарядах нет. Величину поля в каждой точке пространства можно определить, используя принцип суперпозиции, ведь поле, создаваемое точечным источником хорошо известно.
Так что говорить о размещении пробных зарядов в точках , и нет необходимости, ведь у Вас все равно нет, скажем, динамометра, чтобы определять силы, жействующие на пробные заряды, а есть только картинка 🙂
не понятно, почему в точках А и С поля будут направлены в разные стороны, у меня получается, что как раз в одну сторону.
В точке А поля от обоих зарядов направлены в разные стороны, поэтому они друг друга частично сокращают. Аналогично для точки С.
Напряженность электрического поля измеряют с помощью пробного заряда Если величину пробного заряда уменьшить в n раз, то модуль напряженности измеряемого поля
2) увеличится в n раз
3) уменьшится в n раз
4) увеличится в раз
Сила, с которой электрическое поле действует на пробный электрический заряд пропорциональна величине этого заряда, поэтому величина напряженности электрического поля не зависит от величины пробного заряда
по этой формуле же увеличится в n раз
Читайте внимательнее. Сила, действующая на пробный заряд, пропорциональна его величине. Если бы напряженность зависела от величины заряда, то какой бы был прок в такой характеристике поля?
Для электрической напряженности также существует формула E=k*q/r^2. по ней напряженность и заряд прямопропорциональны. как быть?
Напряженность создает другой заряд, который не изменяется.
Металлическому полому телу, сечение которого представлено на рисунке, сообщен отрицательный заряд. Каково соотношение между потенциалами точек 1, 2 и 3, если тело помещено в однородное электростатическое поле?
1)
2)
3)
4)
Металл является проводником. Проводник, помещенный в электростатическое поле является эквипотенциальным телом, то есть все его точки находятся под одинаковым потенциалом. Действительно, если предположить обратное и допустить, что в проводнике есть точки с разными потенциалами, то между этими точками будет ненулевая разность потенциалов, а значит, эти точки проводника будут находиться под ненулевым электрическим напряжением, но тогда в проводнике должен течь ток, что противоречит исходному предположению о том, что все электростатично. Таким образом, при помещении проводника в электростатическое поле заряды на его поверхности всегда перераспределяются таким образом, чтобы потенциал всех точек был одинаковым. Более того, если в проводнике имеется полость, то все точки полости также имеют потенциал, совпадающий по величине с потенциалом проводника. Это явление называется экранировкой электростатического поля. Таким образом, верно утверждение 1.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/elektricheskoe-pole/vektor-naprjazhennosti-elektricheskogo-polja/
http://phys-ege.sdamgia.ru/test?theme=240
[/spoiler]
Законом Кулона описывается взаимодействие заряженных частиц. Однако большинство сил, с которыми мы работали, возникает при взаимодействии тел посредством контакта (т.е. тела касаются друг друга). В случае электромагнитного взаимодействия контакта нет, тогда взаимодействие происходит посредством неких невидимых элементов. Тогда взаимодействия между частицами вещества и удалёнными друг от друга макроскопическими телами осуществляются через посредство физических полей, которые создаются этими частицами или телами в окружающем пространстве. В случае с заряженными частицами, эти поля назовём электромагнитными.
Тогда логика электромагнитного взаимодействия такова: заряд создаёт вокруг себя электромагнитное поле, которое, в свою очередь, действует на любой другой заряд
, находящийся на любом расстоянии от источника.
Закон Кулона описывает взаимодействие между двумя зарядами:
(1)
- где

Рис. 1. Закон Кулона. Пробный заряд
Сила (1) зависит от обоих зарядов, что не позволяет толком описать электрическое поле, создаваемое каждым из взаимодействующих частиц. Тогда придумаем немного другую систему: возьмём пробный заряд — некий малый заряд, который не будет искажать поле исследуемого нами заряда
. Поместим пробный заряд в различные точки пространства рядом с исследуемым нами зарядом и проиллюстрируем силы Кулона (рис. 1).
В принципе, значение силы Кулона можно найти в любой точке пространства, однако данные силы зависят как от заряда источника, так и от значения пробного заряда. Введём новую переменную, поделив значение силы Кулона на значение пробного заряда:
(2)
- где
— вектор напряжённости электрического поля.
Подставим силу Кулона в (1):
(3)
Исходя из (3), можно заключить, что напряжённость электрического поля зависит от заряда источника поля и точки наблюдения, описываемой расстоянием от заряда (рис. 2).

Рис. 2. Напряжённость электрического поля
Т.е. напряжённость электрического поля — параметр, описывающий поле, создаваемое зарядом-источником. Значение напряжённости электрического поля позволяет оценить сильно или слабо будет действовать поле на заряд, помещённый в него. Размерность — В/м.
Исходя из (3), можно найти напряжённость поля точечного заряда. Напряжённость электрического поля — величина векторная, поэтому для её нахождения необходимо знать как модуль, так и направление вектора. Начнём с модуля:
(4)

Рис. 3. Напряжённость электрического поля (направление)
Чтобы выяснить направление вектора, воспользуемся уравнением (2). Исходя из (2), можно заключить, что направление напряжённости электрического поля совпадает с направлением силы Кулона, а направление силы Кулона зависит от знака взаимодействующих зарядов. Чтобы не заморачиваться с рассмотрением этих зарядов в каждой задаче, просто договоримся. Если источник поля (заряд) положителен, тогда напряжённость поля направлена от заряда, если источник поля (заряд) отрицателен, тогда напряжённость поля направлена к заряду (рис. 3).
Напряжённость системы зарядов. Принцип суперпозиции напряжённости.
В случае, если в задаче источниками поля являются несколько зарядов, тогда напряжённость в интересующей точке можно найти как векторную сумму напряжённостей от каждого из зарядов:
(5)
Важно: поиск векторной суммы чаще всего сопряжён с реализацией теоремы Пифагора, теоремы косинусов или синусов, иногда с проецированиием векторов напряжённости на оси с последующим суммированием.

Рис. 4. Принцип суперпозиции напряжённости
Проиллюстрируем: пусть в системе присутствует 3 заряда (,
,
), найти напряжённость в точке А, находящейся на заданном расстоянии от каждого из них (
,
,
) (рис. 4).
Пользуясь знаниями о зарядах, расставляем направления напряжённостей от каждого из зарядов, значение модуля каждой из них можем найти из (4). А далее геометрически складываем, получая искомый .
Напряжённость поля бесконечной заряженной плоскости.
Отдельно в школьной физике рассматривается бесконечная (осень большая) заряженная равномерно плоскость (рис. 5).

Рис. 5. Напряжённость бесконечной плоскости
Напряжённость такой плоскости вблизи её:
(6)
В (6) использовалось определение поверхностной плотности заряда:
(7)
Важно: напряжённость бесконечной плоскости не зависит от расстояния от плоскости.
Напряжённость поля двух бесконечных заряженных плоскостей (конденсатор).

Рис. 6. Напряжённость двух бесконечных плоскостей
Если составить систему из двух бесконечных плоскостей, заряженных одинаковым по модулю и различным по знаку зарядом (при этом площади плоскостей одинаковы), то общая напряжённость между ними:
(8)
Уравнение (8) характеризует напряжённость внутри конденсатора (рис. 6).
Вывод: в случае, если в задаче требуется найти напряжённость, она дана, достаточно рассмотреть систему. Различных систем, а соответственно, и формул, немного: точечный заряд, шар, система точечных зарядов и бесконечные плоскости. Для каждой системы — своё решение.
1 Вектор напряженности поля (шпоры к экзамену)
2022-01-252022-01-25СтудИзба
Описание файла
Документ из архива “шпоры к экзамену”,
который расположен в категории “”.
Всё это находится в предмете “физика” из 3 семестр, которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана.
Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. .
Онлайн просмотр документа “1 Вектор напряженности поля”
Текст из документа “1 Вектор напряженности поля”
|
1 1 2
3)Равномерно заряженное кольцо. Разобьем кольцо на большое количество участков(
2 Закон полного тока: сила полного тока равна сумме тока проводимости и тока смещения Токи смещения появляются только в том случае, если эл. смещение переменно |
1 Э Э |
1 г з характеризует плотность выделенной энергии 2 В естественном свете все направления колебаний вектора E (относительно луча) являются равновероятными, т.к. волна естественного света – это результат суперпозиции волн от большого количества излучающих атомов. Поляризованный свет – это свет, в котором направление колебаний вектора напряжённости эл. поля каким-то образом упорядочено. Если вектор E колеблется в одной плоскости, содержащей луч, то говорят, что свет является плоско (или линейно) поляризованным. Если вектор E вращается вокруг луча, то говорят об эллиптической поляризации. (Круговая поляризация – это частный случай эллиптической поляризации) З П |
|
1 2Энергия и импульс электромагнитного поля Объемн. Пл. w энергии эм волны складывается из объемных эл. и магн. полей: wэл = wм. Умножив плотность энергии w на скорость v распространения волны в среде получим модуль плотности потока энергии: T.к. векторы Е и Н взаимно Ʇ и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ЕН] совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН. Импульс электромагнитного поля |
2 Плоская электромагнитная волна – монохроматическая электромагнитная волна, фазовые фронты которой представляют собой // друг другу плоскости. 1) Плоская электромагнитная волна является поперечной. 2) Колебания напряженностей электрического и магнитного полей в любой точке плоской волны происходят с одинаковой фазой. Электромагнитную волну называют плоской, если векторы
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид: г П |
1 Проводники с током в магн. поле З с 2 В неоднородной среде световые волны дифрагируют на неоднородностях среды – рассеиваются. Среды с ярко выраженной оптической неоднородностью называют мутными(пример: дымы, туманы) |
|
1 1) движется равномерно и прямолинейно. 2)
3 В 2 Шкала электромагнитных излучений показывает, как один качественный вид излучений переходит в другой по мере того, как изменяются взаимосвязанные количественные показатели частоты, длины волны. Один из видов диапазонов излучений — видимый свет. Оптическое излучение-энергия переносимая излучением оптической области спектра (с λ от 100нм до и |
1 Для определения условий на границе двух однородных магнетиков используют теорему Гаусса для вектора В: 1)Для В
2)Для Н – Пусть вдоль границы раздела магнетиков течёт поверхностный ток проводимости с линейной плотностью i. Выбираем прямоугольный контур, высота которого пренебрежимо мала по сравнению с его длиной l. Е
П
2 Интерференция:1)применяется для подтверждения волновой природы света2) для измерения длин волн(интерференционная спектроскопия). 3) для улучшения качества оптических приборов(просветление оптики) и получения высокоотражающих покрытий. Интерферометры – очень чувствительные оптические приборы, позволяющие определять незначительные изменения показателя преломления прозрачных тел (газов, жидких и твердых тел) в зависимости от давления, температуры, примесей и т. д. |
1 Потоком вектора магнитной индукции (магнитным потоком) через ориентированную пов-сть S называется величина В т в диф. форме 2 Интерференция волн – взаимное усиление или ослабление когерентных волн при их наложении друг на друга. Применительно к электромагнитным волнам это означает, что плоскости поляризации волн должны быть одинаковыми. Рассмотрим такие две плоские электромагнитные волны, распространяющиеся в разных направлениях, у которых плоскости поляризации // оси Z. Пусть амплитуды волн одинаковые. Вдоль лучей уравнения волн будут иметь вид + по принципу суперпозиции Е=Е1+Е2= Ш
|
|
|
1 Магнитное поле в веществе складывается из 2 полей: внешнего Д 2 При прохождении света через оптически анизотропные кристаллы наблюдается явление двойного лучепреломления, которое состоит в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся с различными скоростями и в различных направлениях. |
1 1 2
2 Условие максимума интерференции в отраженном свете Кольца Ньютона
« пластина имеет форму тонкого клина (d # const) и освещается параллельным пучком света(i = const) разность хода зависитот толщины пластины в том или ином ее месте « |
1 Теорема о циркуляции намагниченности в интегральной форме: Дифференциальная теорема о циркуляции намагниченности: 2 Когерентность – это согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны – неограниченные в пространстве волны постоянной частоты (w = const) Временная когерентность – это согласованность фаз и частот колебаний в данной точке пространства волнового поля в различные моменты времени. Пространственная когерентность означает, что определенные фазовые соотношения сохраняются неизменными в течение некоторого времени не только в данной точке пространства, но и между колебаниями, происходящими в разных точках пространства. Пространственная и временная когерентности связаны с реальной немонохроматичностью световых волн (существует не одна единственная частота излучения w, а некоторый разброс ее значений Dw и связанный с этим разброс направлений волнового вектора |
|
|
1 Магнитное поле в веществе складывается из 2 полей: внешнего Д 2 При прохождении света через оптически анизотропные кристаллы наблюдается явление двойного лучепреломления, которое состоит в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся с различными скоростями и в различных направлениях. В зависимости от типа симметрии оптически анизотропные кристаллы бывают одноосные либо двуосные, т.е. имеют одну или две оптические оси. Оптической осью называется такое направление в кристалле, вдоль которого распространяющийся свет не испытывает двойного лучепреломления. У обыкновенного луча – скорость не зависит от направления и = лучевой скорости с направлением коллинеарным оптической оси. Необыкновенный – если у луча эл. вектор находится в главной плоскости, его скорость зависит от направления. Поляроид (поляризационный светофильтр) – один из основных типов оптических линейных поляризаторов; представляет собой тонкую поляризационную плёнку, заклеенную для защиты от механических повреждений и действия влаги между двумя прозрачными пластинками (плёнками) |
1 Магнитное поле -это силовое поле, действующее на движущиеся электрические заряды (токи) и на тела, обладающие магнитным м С 2 дифракционная решетка, представляет собой множество параллельных, расположенных на равных расстояниях одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. П
Спектр.хар.: 1). Угловая дисперсия. Угловая дисперсия определяет угловое расстояние между двумя спектральными линиями, отличающимися на единицу длины волны .2) Дисперсионная область. Максимальная ширина спектрального интервала , при которой нет перекрытия, называется дисперсионной областью спектрального аппарата 3) Разрешающая способность. Наименьшая разность длин волн двух спектральных линий , при которой спектральный аппарат разрешает эти линии, называется спектральным разрешаемым расстоянием а величина R / разрешающей способностью аппарата |
1 н
вывод: при переходе через границу раздела двух диэлектриков линии вектора напряженности электрического поля и линии электрического смещения преломляются. 2 Дифракция рентгеновского излучения является результатом его отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решетки). Ф (m=1,2,…) θ-угол скольжения |
Свежие статьи
Популярно сейчас
Зачем заказывать выполнение своего задания, если оно уже было выполнено много много раз? Его можно просто купить или даже скачать бесплатно на СтудИзбе. Найдите нужный учебный материал у нас!
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
575
Средний доход
с одного платного файла
Обучение Подробнее
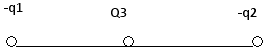


 , при ∑ всех векторов напряженностей от каждого из участков будем учитывать только составляющую вектора, // оси кольца, длина которой
, при ∑ всех векторов напряженностей от каждого из участков будем учитывать только составляющую вектора, // оси кольца, длина которой  ) Частица движется под углом к линиям магн. индукции. Тогда ее движение будет суммой двух движений-равномерного прямолинейного и равномерного по окр., тогда суммарное – по спирали.Шаг винтовой линии
) Частица движется под углом к линиям магн. индукции. Тогда ее движение будет суммой двух движений-равномерного прямолинейного и равномерного по окр., тогда суммарное – по спирали.Шаг винтовой линии 
 сли на границе раздела тока проводимости нет, то тангенциальная составляющая вектора не испытывает скачка:
сли на границе раздела тока проводимости нет, то тангенциальная составляющая вектора не испытывает скачка: случае, когда площадка – плоская, а магнитное поле – однородное магнитный поток равен: ΦB=B⋅S⋅cosα, где S – величина площади, B – величина индукции, α – угол между нормалью n к площадке контура и вектором B .
случае, когда площадка – плоская, а магнитное поле – однородное магнитный поток равен: ΦB=B⋅S⋅cosα, где S – величина площади, B – величина индукции, α – угол между нормалью n к площадке контура и вектором B . Для магнитного поля справедлив принцип суперпозиции: в каждой точке пространства вектор магнитной индукции созданных в этой точке
Для магнитного поля справедлив принцип суперпозиции: в каждой точке пространства вектор магнитной индукции созданных в этой точке  при интерференции в тонких пленках теряется полуволна
при интерференции в тонких пленках теряется полуволна полосы равной толщины»
полосы равной толщины»  полосы равного наклона».При d = const (плоскопараллельная пластина) разность хода определяется только углом падения
полосы равного наклона».При d = const (плоскопараллельная пластина) разность хода определяется только углом падения ериод дифр. решетки – расстояние между серединами соседних щелей
ериод дифр. решетки – расстояние между серединами соседних щелей  тангенциальная составляющая вектора напряженности электрического поля при переходе через границу двух диэлектриков непрерывна.
тангенциальная составляющая вектора напряженности электрического поля при переходе через границу двух диэлектриков непрерывна. ормула Вульфа-Брэггов:
ормула Вульфа-Брэггов: 