Нам кажется, что на видео есть . Посмотреть
Уберите лишние метки и подтвердите оставшиеся, если они определены верно
Убраны из меток0
Подтвердить метки
Отмена
Как найти сумму чисел от 1 до 10…
На видео отмечены:
5 марта 2022141 просмотр
-
Комментарии0
-
0
-
Добавить в закладки
-
-
Пожаловаться
-
Microsoft Excel – мощный программный инструмент для работы с электронными таблицами. В программе можно составлять таблицы и отчеты, производить расчеты любой сложности, строить диаграммы, графики и многое другое. Довольно часто Эксель используют для того, чтобы вычислить итоговую сумму в столбцах и строках таблицы, или, например, чтобы узнать сумму нескольких ячеек. В этом уроке мы с вами научимся считать сумму ячеек в программе Microsoft Excel благодаря пошаговой инструкции.
Автосумма
Данная функция является одной из самых популярных и комфортных для расчета суммы значений в ячейках таблицы. Для этого нужно сделать следующее:
- Переходим в вкладку “Главная”, левой кнопкой мыши (далее – ЛКМ) нажимаем на последнюю пустую ячейку столбца или строки, по которой нужно посчитать итоговую сумму и нажимаем кнопку “Автосумма”.
- Затем в ячейке автоматически заполнится формула расчета суммы.
- Чтобы получить итоговый результат, нажимаем клавишу “Enter”.
Чтоб посчитать сумму конкретного диапазона ячеек, ЛКМ выбираем первую и последнюю ячейку требуемого диапазона строки или столбца.
Далее нажимаем на кнопку “Автосумма” и результат сразу же появится в крайней ячейке столбца или ячейки (в зависимости от того, какой диапазон мы выбрали).
Данный способ достаточно хорош и универсален, но у него есть один существенный недостаток – он может помочь только при работе с данными, последовательно расположенными в одной строке или столбце, а вот большой объем данных подсчитать таким образом невозможно, равно как и не получится пользоваться “Автосуммой” для отдаленных друг от друга ячеек.
Допустим, мы выделяем некую область ячеек и нажимаем на “Автосумма”.В итоге мы получим не итоговое значение по всем выделенным ячейкам, а сумму каждого столбца или строки по отдельности (в зависимости от того, каким образом мы выделили диапазон ячеек).
Функция “Сумм”
Данная функция в Microsoft Excel позволяет суммировать значения большого массива данных. Для этого необходимо сделать следующее:
- ЛКМ выделяем ячейку, в которую планируем вывести итоговый результат, далее нажимаем кнопку «Вставить функцию», которая находится с левой стороны строки формул.
- В открывшемся списке “Построителя формул” находим функцию “СУММ” и нажимаем “Вставить функцию” (или “OK”, в зависимости от версии программы). Чтобы быстро найти нудную функцию можно воспользоваться полем поиском.
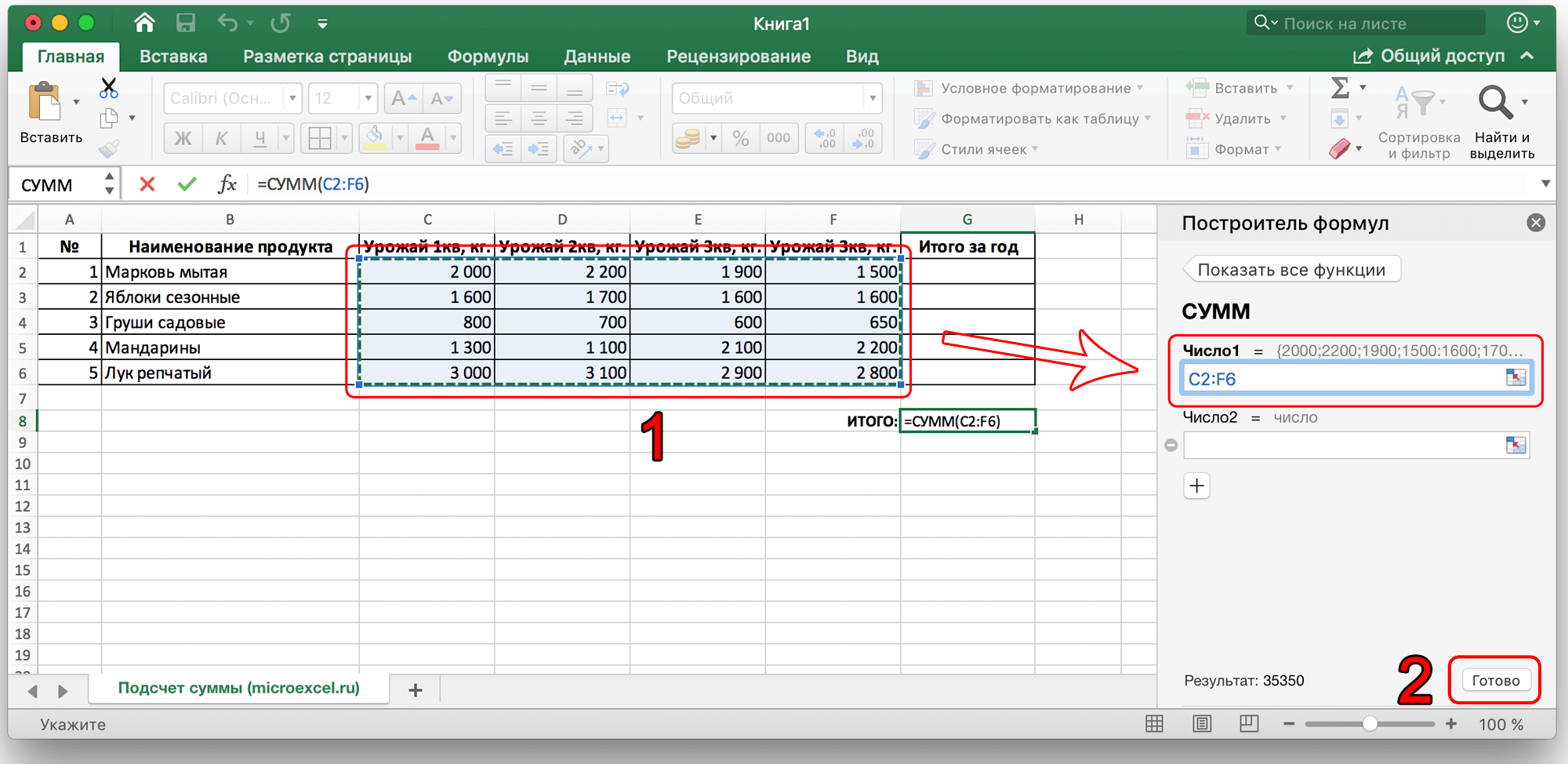
- В появившемся окне по настройке функции указываем имена ячеек, которые необходимо сложить. Разумеется, самостоятельно набирать адрес ячеек можно, но вовсе не обязательно. Вместо этого можно выбрать нужный нам диапазон ячеек, выделив его ЛКМ.
- Если нужно выбрать еще один диапазон данных, щелкаем ЛКМ на поле “Число 2” и выбираем его аналогично процедуре, описанной выше. Добавлять новые диапазоны можно практически бесконечно, каждый раз нажимая кнопку “+” под последним.
- После того, как все нужные ячейки выделены, нажимаем кнопку “Готово”.
- После этого мы видим результат в ранее выбранной ячейке.
Работа с формулами
В программе Эксель можно посчитать сумму с помощью простой формулы сложения. Делается это следующим образом:
- ЛКМ выделяем ячейку, в которой хотим посчитать сумму. Затем, либо в самой ячейке, либо перейдя в строку формул, пишем знак “=”, ЛКМ нажимаем на первую ячейку, которая будет участвовать в расчетах, после нее пишем знак “+”, далее выбираем вторую, третью и все требуемые ячейки, не забывая между ними проставлять знак “+”.
- После того, как формула готова, нажимаем “Enter” и получаем результат в выбранной нами ячейке.
Основным минусом данного способа является то, что сразу отобрать несколько ячеек невозможно, и необходимо указывать каждую по отдельности.
Просмотр суммы в программе Excel.
Помимо расчета суммы в отдельной ячейке, в программе Microsoft Excel можно просто просматривать сумму значений выбранных ячеек. Но это работает только при условии, что все ячейки располагаются рядом.
- Выделяем диапазон ячеек, сумму по которым мы хотим посмотреть.
- Смотрим вниз на результат, который отображается в строке состояния программы.
Помимо общей суммы, мы также видим количество выделенных ячеек и среднее значение по ним.
Как Вы могли заметить, программа Эксель позволяет решать задачу суммирования разными способами. Каждый из них имеет свои достоинства и недостатки, свою сложность и продуктивность в зависимости от поставленной задачи и ее специфики.
марина сашина
446
19.07.2013
Комментировать
Нравится2Нравится2 людям
Войдите
в Мой Мир, чтобы комментировать
Самое теплое местечко
Супер топ
32 980
22.05.2023
Нравится14Нравится14 людям
Войдите
в Мой Мир, чтобы комментировать
Скульптура
Супер топ
7 551
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Тьма хочет кушать
Супер топ
6 898
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Шедевральное интервью
Супер топ
2 780
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Зевота заразительна
Супер топ
2 946
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Когда ты шикарен со всех сторон
Супер топ
2 915
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Бывают дни – когда всё с рук валится
Супер топ
2 204
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Воспитанный собакой поросёнок
Супер топ
1 763
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Достаточно одного слабого звена в цепочке…
Супер топ
2 290
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Жидкoсть инcтинктивнo ищeт ёмкocть
Супер топ
2 115
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Интересно, в каком виде в итоге доедут посылки???
Супер топ
1 840
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Наблюдатель
Супер топ
1 613
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Котик и лук
Супер топ
1 548
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Не шути с автомобильным пылесосом
Супер топ
1 439
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Пушинка
Супер топ
1 424
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Когда уходишь в отрыв
Супер топ
1 422
22.05.2023
Нравится1Нравится1 человеку
Войдите
в Мой Мир, чтобы комментировать
Аж в глазах помутнело
Супер топ
1 105
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Гиперактивный игруля
Супер топ
1 156
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Посадка вертолёта на движущийся корабль
Супер топ
1 002
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Вместительный однако
Супер топ
1 029
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Во даёт!
Супер топ
1 061
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Отражение
Войдите
в Мой Мир, чтобы комментировать
Вот поэтому я так не делаю
Войдите
в Мой Мир, чтобы комментировать
Допрыгалась
Супер топ
1 195
22.05.2023
Войдите
в Мой Мир, чтобы комментировать
Содержание
- Сумма и разность чисел
- Что такое сумма, и как ее найти
- Как найти разность чисел
- Как найти разность чисел в математике
- Арифметические действия с числами
- Разность в математике
- Видео: Математика 6 Делимость суммы и разности чисел
- Как найти разницу величин
- Математические действия с разностью чисел
- Видео: Математика 2 класс. Разность двухзначных чисел
- Простые примеры
- Более сложные примеры
- Математика для блондинок
- Свойства сложения и вычитания
- Свойства сложения
- Свойства вычитания
- Примеры использования свойств сложения и вычитания
Сумма и разность чисел
Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел

В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Источник
Как найти разность чисел в математике

Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
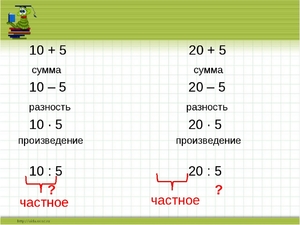
- сумма — результат, получившийся при сложении чисел;
- разность — результат, получившийся при вычитании чисел;
- произведение — результат умножения чисел;
- частное — результат деления.
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить;
- разность — отнять;
- произведение — умножить;
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
Разность чисел означает, насколько одно из них больше другого.
- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
Видео: Математика 6 Делимость суммы и разности чисел
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
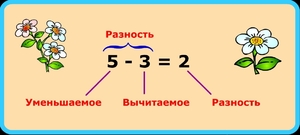
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Видео: Математика 2 класс. Разность двухзначных чисел
Простые примеры
- Пример 1. Найти разницу двух величин.
20 — уменьшаемое значение,
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
- Пример 2. Найти уменьшаемое.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
- Пример 3. Найти вычитаемое значение.
17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
7 — уменьшаемая величина;
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Источник
Свойства сложения и вычитания
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое,
- 5 — второе слагаемое,
- 7 — это сумма.
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
- Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
a + b = b + a - Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c) - Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
При этом саму запись (9 — 4) тоже можно назвать разностью.

- Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
a — 0 = a
Если из числа вычесть само число, то получится нуль.
a — a = 0 - Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
a — (b + c) = a — b — c - Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) — c = (a — c) + b (если a > c или а = с)
(a + b) — c = (b — c) + a (если b > c или b = с)
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:
Пример 1
Вычислить сумму слагаемых с использованием разных свойств:
а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15
б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22
в) 30 + 0 + 13 = 30 + 13 = 43
Пример 2
Применить разные свойства при вычислении разности:
а) 25 — 0 — 2 = 25 — 2 = 23
б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13
Пример 3
Найти значение выражения удобным способом:
а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32
б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16
Источник
Давайте разберёмся, что же происходит когда
складывают два числа.
Например,
прибавим к числу 2 число 4.
Для наглядности изобразим сложение этих чисел на
горизонтальной координатной прямой.
Мы знаем, что положительным числом
указывают перемещение точки вправо по координатной прямой. То есть
2 + 4, означает, что точка с координатой 2 переместилась вправо на 4
единичных отрезка и перешла в точку с координатой 6.
А что произойдёт, если к числу 2 прибавить число –
4, противоположное числу 4?
Понятно, что точка с координатой 2 переместится на 4
единичных отрезка влево, так как отрицательным числом указывают перемещение
точки влево по координатной прямой. А значит, перейдёт в точку с
координатой – 2.
Правило:
Прибавить к числу а число b,
значит изменить число а на b
единиц.
Любое число от прибавления положительного числа
увеличивается, а от прибавления отрицательного числа уменьшается.
Вообще, когда к числу а прибавляют
положительное число b,
то точка с координатой а перемещается на единичных
отрезков вправо.
А когда к числу а прибавляют отрицательное
число b, то точка с
координатой а перемещается на единичных
отрезков влево.
Зная это правило, легко находить сумму чисел
на координатной прямой.
Давайте потренируемся.
Пример 1
Найти сумму чисел – 5
и 9.
Пример 2
Найти сумму 3 и – 5.
Пример 3
Найти сумму чисел – 1
и – 3.
Пример 4
Найти сумму чисел 7
и – 7.
Можно сделать вывод: сумма двух противоположных
чисел равна нулю.
Пример 5
Найти сумму чисел – 6
и 0.
Сделаем ещё один важный вывод: от прибавления
нуля число не изменяется.
Итоги
Итак, сегодня на уроке мы научились складывать
положительные и отрицательные числа при помощи координатной прямой.


 Чтоб посчитать сумму конкретного диапазона ячеек, ЛКМ выбираем первую и последнюю ячейку требуемого диапазона строки или столбца.
Чтоб посчитать сумму конкретного диапазона ячеек, ЛКМ выбираем первую и последнюю ячейку требуемого диапазона строки или столбца. Далее нажимаем на кнопку “Автосумма” и результат сразу же появится в крайней ячейке столбца или ячейки (в зависимости от того, какой диапазон мы выбрали).
Далее нажимаем на кнопку “Автосумма” и результат сразу же появится в крайней ячейке столбца или ячейки (в зависимости от того, какой диапазон мы выбрали). Данный способ достаточно хорош и универсален, но у него есть один существенный недостаток – он может помочь только при работе с данными, последовательно расположенными в одной строке или столбце, а вот большой объем данных подсчитать таким образом невозможно, равно как и не получится пользоваться “Автосуммой” для отдаленных друг от друга ячеек.
Данный способ достаточно хорош и универсален, но у него есть один существенный недостаток – он может помочь только при работе с данными, последовательно расположенными в одной строке или столбце, а вот большой объем данных подсчитать таким образом невозможно, равно как и не получится пользоваться “Автосуммой” для отдаленных друг от друга ячеек. В итоге мы получим не итоговое значение по всем выделенным ячейкам, а сумму каждого столбца или строки по отдельности (в зависимости от того, каким образом мы выделили диапазон ячеек).
В итоге мы получим не итоговое значение по всем выделенным ячейкам, а сумму каждого столбца или строки по отдельности (в зависимости от того, каким образом мы выделили диапазон ячеек).





 Основным минусом данного способа является то, что сразу отобрать несколько ячеек невозможно, и необходимо указывать каждую по отдельности.
Основным минусом данного способа является то, что сразу отобрать несколько ячеек невозможно, и необходимо указывать каждую по отдельности.
 Помимо общей суммы, мы также видим количество выделенных ячеек и среднее значение по ним.
Помимо общей суммы, мы также видим количество выделенных ячеек и среднее значение по ним.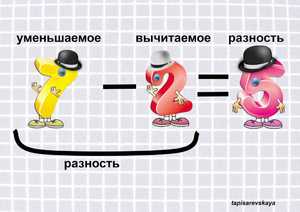 Разность чисел означает, насколько одно из них больше другого.
Разность чисел означает, насколько одно из них больше другого.

