Сегодня на уроке мы научимся складывать и вычитать
смешанные числа.
На прошлом уроке мы с вами уяснили, что сумму
натурального числа и правильной дроби принято записывать без знака «+». Такую
сумму называют смешанным числом. Натуральное число называют целой
частью смешанного числа, а дробь – дробной частью смешанного числа. То есть
При сложении смешанных чисел пользуются переместительным
и сочетательным свойствами сложения.
Пример
Найти сумму чисел и
.
В записи в тетрадях не стоит расписывать, как вы
считаете достаточно написать:
Таким образом, чтобы сложить смешанные числа,
нужно сложить по отдельности их целые и дробные части и записать сумму
полученных чисел.
Иногда при сложении смешанных чисел в их дробной
части может получиться неправильная дробь. В этом случае из неё выделяют
целую часть, и добавляют её к уже имеющейся дробной части.
Пример
Найти сумму чисел и
.
Таким образом, если при сложении дробных
частей получилась неправильная дробь, то выделяют целую часть этой дроби и
добавляют к уже имеющейся целой части.
Задача
На столе лежало 2 яблока. Принесли ещё 1
яблока. Сколько яблок лежит на столе?
Решение
Посмотрите, что получилось: складывали смешанные
числа, а ответ выражен натуральным или можно ещё сказать целым числом.
При вычитании смешанных чисел пользуются свойством
вычитания числа из суммы и свойством вычитания суммы из числа.
Пример
Найти разность дробей и
.
В тетрадях пишут короче:
Таким образом, чтобы найти разность смешанных
чисел, нужно найти отдельно разность целых частей и отдельно разность дробных
частей.
Есть в примерах на вычитание и «особые» случаи.
Например
Вычтем из дроби дробь
.
Запомните! Не начинайте выполнять вычитание, пока
не убедитесь, что из числителя первой дроби можно вычесть числитель второй
дроби.
Иногда в примерах нужно вычесть из натурального
числа смешанную дробь.
Например
Найдём значение выражения .
Итоги
Чтобы сложить смешанные числа, нужно сложить по
отдельности их целые и дробные части и записать сумму полученных чисел.
Если при сложении дробных частей получилась
неправильная дробь, выделить целую часть из этой дроби и прибавить её к
полученной целой части.
Чтобы найти разность смешанных чисел, нужно найти
отдельно разность целых частей и отдельно разность дробных частей.
Если дробная часть уменьшаемого меньше дробной части
вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую
часть.
Целая, дробная части действительного числа и их свойства
Теперь, когда сформулировано понятие действительного числа, можно ввести ещё два связанных между собой понятия, характеризующих данное действительное число — его целую и дробную части. Определения целой и дробной частей имеют словесно-описательную форму.
Целой частью действительного числа x называется наибольшее целое число, не превосходящее x, и обозначается [х]. Дробной частью действительного числа x называется разность между самим числом и его целой частью, т.е. x -[х], и обозначается {x}. Например: [5,12] = 5, {5,12} = 0,12; [—5,12] = —6, {-5,12}= 0,88; 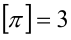
Из определений целой и дробной частей вытекают их основные свойства. Рассмотрим их. Пусть x ,у — произвольные действительные числа, n — любое целое число. Тогда справедливы следующие утверждения.
Свойства целой и дробной частей
1. Целая часть любого действительного числа x есть целое число:
2. Любое действительное число x можно представить в виде суммы его целой и дробной частей, т.е.
3. Любое действительное число x всегда заключено между своей целой частью (с которой может совпадать) и числом, на единицу большим целой части, т.е.
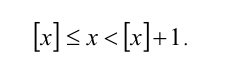
4. Дробная часть любого действительного числа x может принимать значения в пределах от 0 (наименьшее возможное значение) до 1 (это значение не достигается ни при каком x), т.е.
5. Любое целое число n можно выносить (или вносить) из-под знака целой части, т.е.
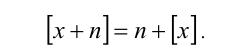
Добавление (или вычитание) к действительному числу x произвольного целого числа n не изменяет значения его дробной части, т.е.
6. Целая часть суммы двух действительных чисел не меньше суммы их целых частей, т.е.
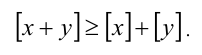
Докажем, например, последнее свойство:
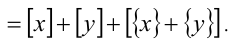
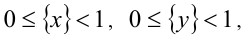
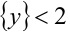
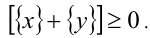
7. Дробная часть суммы двух действительных чисел не больше суммы их дробных частей, т.е.
Доказательство. Воспользуемся предыдущим свойством:
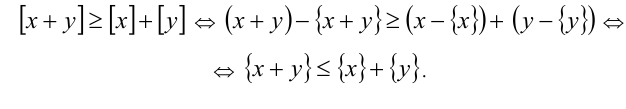
Для построения графиков функций 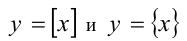
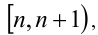
Так, на полуинтервалах вида 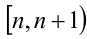
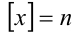
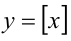
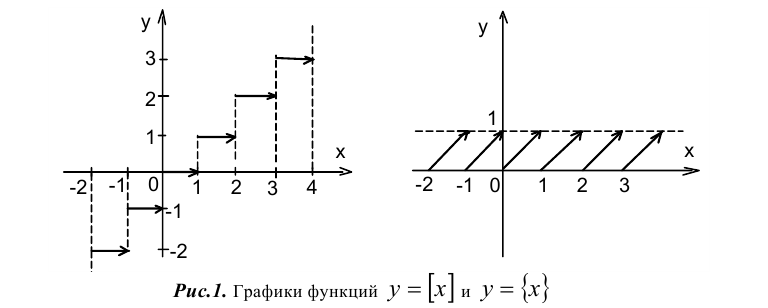
Далее, на рассматриваемом промежутке 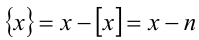
Видно, что обе функции терпят разрывы в виде конечных скачков значений при целочисленных значениях аргумента x. Дробная часть к тому же является периодической функцией с периодом, равным единице. Данные функции не относят к классу элементарных функций.
Заметим, что данный подход, основанный на разбиении числовой прямой на отдельные промежутки, на каждом из которых значения целой и дробной частей можно посчитать, используется и при решении других задач на эту тему, в частности при решении уравнений. В экзаменационных вариантах задачи на свойства целой и дробной частей встречаются достаточно редко и в основном на математических факультетах, однако надо быть готовым к решению задач такого рода.
Пример №101.
Решить неравенство
Решение:
Заменим x в правой части неравенства на сумму [х] + {х} :
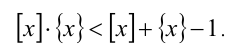
Приведём неравенство к виду 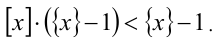
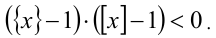
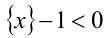

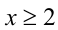
Ответ.
Пример №102.
Решить уравнение { 2х} = x.
Решение:
1-й способ. Заметим, что левая часть уравнения {2х} как величина дробной части может принимать значения, не выходящие за пределы полуинтервала [0,l). Следовательно, и правая часть уравнения, т.е. x, может принимать значения в этих же пределах. Итак, ОДЗ: 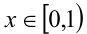
1) Пусть 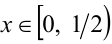
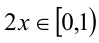
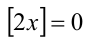
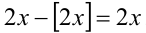
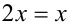
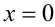
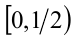
2) Пусть теперь 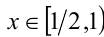
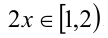
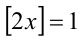
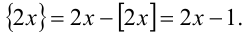
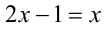
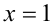
2-й способ (графический). Построим в одной системе координат графики функций 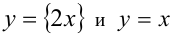
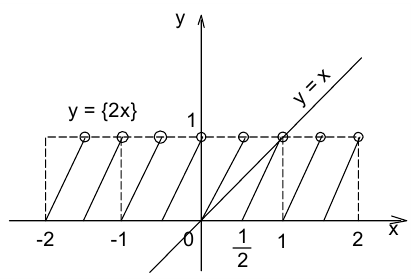
графиков, а сами решения являются абсциссами точек пересечения графиков. Очевидно, что графики пересекаются в единственной точке — начале координат. Проверкой убеждаемся, что число x = 0 действительно является решением данного уравнения (проверку сделать необходимо, поскольку графический способ решения, вообще говоря, неточный).
Пример №103.
Сколько решений имеет уравнение
x + [100x]=100x?
Решение:
Перепишем уравнение в виде x = {100х} . Эту задачу можно решить графически. Рассмотрим другой способ. Так как выражение {100x} может принимать значения лишь из промежутка [0,1), то и 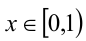
Подставим в исходное уравнение:
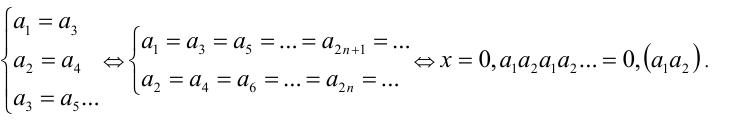
Таким образом, любое число вида 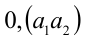
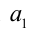
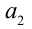
Пример №104.
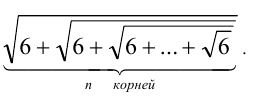
Найти целую часть числа
Решение:
Для решения задачи достаточно оценить, между какими последовательными целыми числами расположено данное число. Обозначим это число через 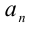
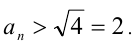
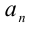
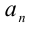
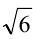
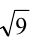
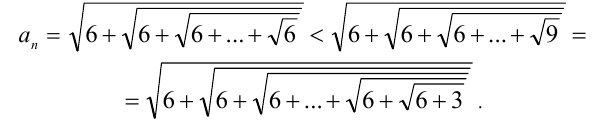
Последовательно упрощая выражение в правой части, получим 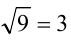
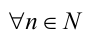
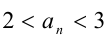
Пример №105.
Решить уравнение
Решение:
Разобьём множество всех действительных значений неизвестной x на промежутки, в которых можно однозначно раскрыть целую часть: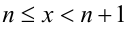
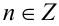
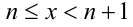
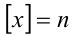
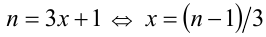
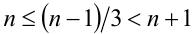
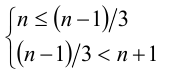
в целых числах, находим 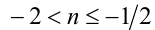
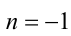
Замечание. Задачу можно было решить, используя графический подход.
Пример №106.
Решить уравнение
Решение:
Положим 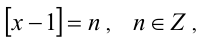
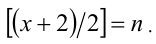
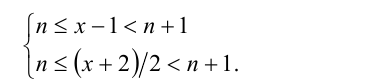
Дальнейшее решение зависит от того, что больше: x —1 или (х + 2)/2. Рассмотрим два случая.
1) Пусть 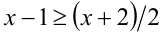
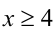
Получаем систему неравенств с двумя неизвестными, одна из которых целочисленна:
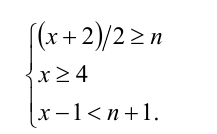
Отсюда 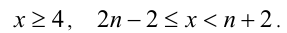
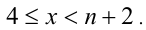
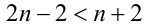
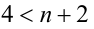
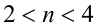
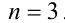
2) Пусть 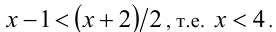
Аналогично первому случаю находим 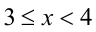
Ответ: 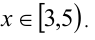
Пример №107.
Решить уравнение
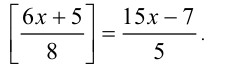
Решение:
Сделаем замену 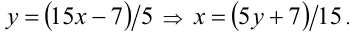
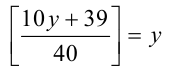
с целочисленной неизвестной у . Раскрывая целую часть по определению, получаем двойное неравенство
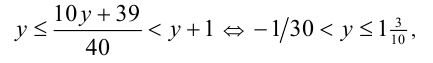
откуда с учётом целочисленности у находим у = 0 или у = 1. Им отвечают значения x = 7/15 и x = 4/5.
Ответ:
Пример №108.
Найти все решения уравнения
Решение:
Упростим уравнение при помощи свойств целой части. Так как 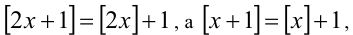
Решим его стандартным методом. Чтобы раскрыть обе целые части, разобьём множество всех действительных x на полуинтервалы 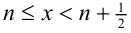
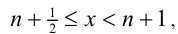
1) Если 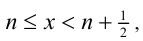
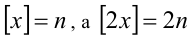
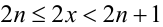
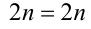
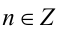
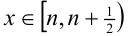
2) Если же 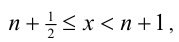
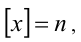
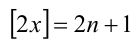
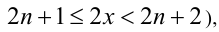
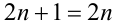
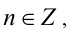
Ответ:
Пример №109.
Найти все решения уравнения {х} = 1/х.
Решение:
ОДЗ: 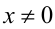
Пусть 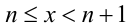
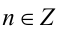
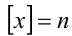
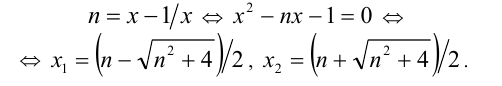
При этом 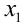
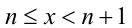
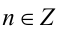
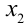
Ответ:
Пример №110.
Найти все натуральные значения n, удовлетворяющие уравнению
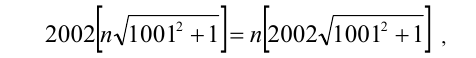
где [х] — наибольшее целое число, не превосходящее числа x.
Решение:
Пусть 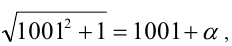
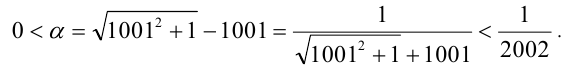
Значит,
Но тогда 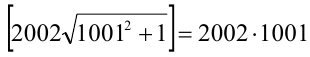
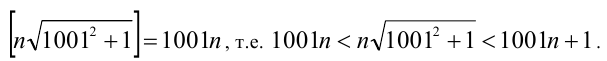
Отсюда
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:
|
Klord 1 / 1 / 2 Регистрация: 28.11.2010 Сообщений: 30 |
||||
|
1 |
||||
Одномерный массив, подскажите как посчитать сумму целых частей …02.03.2011, 19:52. Показов 1262. Ответов 6 Метки нет (Все метки)
Задание:
0 |
|
MILAN 899 / 793 / 186 Регистрация: 21.02.2009 Сообщений: 1,722 |
||||
|
02.03.2011, 20:03 |
2 |
|||
|
Klord,
1 |
|
1 / 1 / 2 Регистрация: 28.11.2010 Сообщений: 30 |
|
|
02.03.2011, 21:05 [ТС] |
3 |
|
Сейчас считает ВСЕ целые части элементов. А по условию он должен считать после последнего отрицательного элемента, то есть после -3.6. И сумма будет равна 13. Если в чем то не прав, поправьте пожалуйста. Очень нужно разобраться и понять!
0 |
|
SRq 2 / 2 / 2 Регистрация: 18.11.2010 Сообщений: 31 |
||||
|
02.03.2011, 21:29 |
4 |
|||
|
Задание:
1 |
|
1 / 1 / 2 Регистрация: 28.11.2010 Сообщений: 30 |
|
|
02.03.2011, 21:35 [ТС] |
5 |
|
SRq, Спасибо! Здесь k получается в роли счетчика?
0 |
|
899 / 793 / 186 Регистрация: 21.02.2009 Сообщений: 1,722 |
|
|
02.03.2011, 22:24 |
6 |
|
Klord, k указывает на номер последнего отрицательного елемента.
А по условию он должен считать после последнего отрицательного элемента Да, недоглядел. Извините.
1 |
|
1 / 1 / 2 Регистрация: 28.11.2010 Сообщений: 30 |
|
|
02.03.2011, 23:20 [ТС] |
7 |
|
MILAN, Все ясно, всем спасибо за помощь.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
02.03.2011, 23:20 |
|
7 |
Смешанные числа так же, как и любые другие числа, можно сравнивать, складывать, вычитать, умножать и делить.
На этом уроке рассмотрим правила сравнения, сложения и вычитания смешанных чисел.
Рассмотрим пример решения текстовой задачи на сложение и вычитание смешанных чисел арифметическим и алгебраическим способом.
Эта информация доступна зарегистрированным пользователям
Смешанное число- это число, состоящее из целой части (натурального числа) и дробной части (дробного числа).
На предыдущем уроке мы узнали, чем правее располагается число на координатном луче, тем оно больше.
Сравнение смешанных чисел сводится к сравнению их целых частей и дробных частей.
Эта информация доступна зарегистрированным пользователям
1. Чтобы ответить на вопрос какое смешанное число больше, а какое меньше используют следующее правило:
Большим считается то смешанное число, целая часть которого больше, если же целые части равны, то больше то смешанное число, у которого дробная часть больше.
Соответственно верно и следующее утверждение: смешанные числа считаются равными, если их целая и дробная часть совпадают.
Рассмотрим примеры.
Пример №1.
Сравните два смешанных числа (mathbf{22frac{6}{7}}) и (mathbf{42frac{5}{7}}).
Решение:
Целая часть смешанного числа (mathbf{22frac{6}{7}}) равна 22.
Целая часть смешанного числа (mathbf{42frac{5}{7}}) равна 42.
Так как 22 < 42, значит и (mathbf{color{orange}{22}frac{6}{7} < color{green}{42}frac{5}{7}}).
Пример №2.
Сравните два смешанных числа (mathbf{26frac{6}{7}}) и (mathbf{26frac{5}{7}}).
Решение:
Целая часть смешанного числа (mathbf{26frac{6}{7}}) равна 26.
Целая часть смешанного числа (mathbf{26frac{5}{7}}) равна 26.
Так как целые части смешанных чисел равны: 26 = 26, сравним их дробные части.
Число (mathbf{frac{6}{7}})- дробная часть смешанного числа (mathbf{26frac{6}{7}}).
Число (mathbf{frac{5}{7}}) дробная часть смешанного числа (mathbf{26frac{5}{7}}).
Для сравнения обыкновенных дробей с одинаковыми знаменателями, необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.
Числитель дроби (mathbf{frac{6}{7}}) больше числителя дроби (mathbf{frac{5}{7}}), значит (mathbf{color{orange}{frac{6}{7}} > color{green}{frac{5}{7}}}).
Следовательно (mathbf{26color{orange}{frac{6}{7}} > 26color{green}{frac{5}{7}}}).
Пример №3.
Сравните два смешанных числа (mathbf{175frac{2}{13}}) и (mathbf{175frac{2}{13}}).
Решение:
Так как целая и дробная часть смешанного числа (mathbf{175frac{2}{13}}) совпадает с целой и дробной частью смешанного числа (mathbf{175frac{2}{13}}), то эти два числа равны.
(mathbf{175frac{2}{13} = 175frac{2}{13} })
2. Сравнение смешанных чисел с натуральными числами.
Эта информация доступна зарегистрированным пользователям
Для данного случая действует такое правило:
Если целая часть смешанного числа больше или равна натуральному числу, то смешанное число больше этого натурального числа.
Если целая часть смешанного числа меньше натурального числа, то смешанное число меньше данного натурального числа.
Разберем несколько поясняющих примеров.
Пример №1.
Сравните два числа 85 и (mathbf{139frac{2}{5}}).
Решение:
Целая часть смешанного числа (mathbf{139frac{2}{5}}) равна 139.
Число 139 больше 85 (заданного натурального числа), значит смешанное число (mathbf{139frac{2}{5}}) больше этого натурального числа.
Получаем следующее неравенство:
(mathbf{85 < 139frac{2}{5}})
Пример №2.
Сравните два числа 147 и (mathbf{147frac{6}{11}}).
Решение:
Натуральное число 147 и целая часть смешанного числа (mathbf{147frac{6}{11}}) равны.
Если целая часть смешанного числа равна натуральному числу, то смешанное число больше этого натурального числа.
Следовательно, смешанное число (mathbf{147frac{6}{11}}) больше натурального числа 147.
(mathbf{147 <147frac{6}{11}})
Пример №3.
Сравните два числа 53 и (mathbf{14frac{6}{18}}).
Решение:
Целая часть смешанного числа (mathbf{14frac{6}{8}}), число 14, меньше заданного натурального числа 53, значит, смешанное число (mathbf{14frac{6}{8}}) меньше натурального числа 53.
(mathbf{53 > 14frac{6}{8}})
3. Сравнение смешанных чисел и обыкновенных дробей.
Эта информация доступна зарегистрированным пользователям
- Сравнение смешанных чисел и правильных дробей.
Так как смешанное число всегда больше единицы, а правильная дробь всегда меньше единицы, то справедливо правило:
Любое смешанное число всегда больше правильной дроби.
- Сравнение смешанных чисел и неправильных дробей.
Сравнение смешанного числа и неправильной дроби можно осуществлять двумя способами.
Первый способ: сравнение смешанного числа и неправильной дроби можно свести к сравнению двух неправильных дробей.
Для этого смешанное число необходимо перевести в неправильную дробь.
Рассмотрим пример.
Сравните смешанное число (mathbf{12frac{3}{8}}) и неправильную дробь (mathbf{frac{105}{8}}).
Решение:
Переведем смешанное число (mathbf{12frac{3}{8}}) в неправильную дробь.
Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.
(mathbf{color{red}{12}frac{color{green}{3}}{color{blue}{8}} = frac{color{red}{12} cdot color{blue}{8} + color{green}{3}}{color{blue}{8}} = frac{96 + color{green}{3}}{color{blue}{8}} = frac{99}{color{blue}{8}}})
Вместо (mathbf{12frac{3}{8}}) подставим соответствующее ему число (mathbf{frac{99}{8}}).
Сравним неправильные дроби (mathbf{frac{99}{8}}) и (mathbf{frac{105}{8}}).
Для сравнения обыкновенных дробей с одинаковыми знаменателями, необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.
99– числитель дроби (mathbf{frac{99}{8}}).
105– числитель дроби (mathbf{frac{105}{8}}).
Так как 99 < 105, то (mathbf{frac{color{orange}{99}}{8} < frac{color{green}{105}}{8}}).
Известно, что неправильная дробь (mathbf{frac{99}{8}}) соответствует смешанному числу (mathbf{12frac{3}{8}}).
В итоге получается следующий результат: (mathbf{12frac{3}{8} < frac{105}{8}}).
Второй способ: сравнение смешанного числа и неправильной дроби можно свести к сравнению двух смешанных чисел.
Для этого неправильную дробь необходимо перевести в смешанное число.
Рассмотрим поясняющий пример.
Сравним смешанное число (mathbf{12frac{3}{8}}) и неправильную дробь (mathbf{frac{105}{8}}).
Решение:
Переведем неправильную дробь (mathbf{frac{105}{8}}) в смешанное число.
Разделим числитель дроби на знаменатель, полученное неполное частное будет представлять собой целую часть смешанного числа, остаток от деления- это числитель дробной части смешанного числа, а делитель- знаменатель.
105 ÷ 8 = 13 (ост. 1)
(mathbf{frac{105}{8} = 13frac{1}{8}})
Сравним два смешанных числа (mathbf{12frac{3}{8}}) и (mathbf{13frac{1}{8}}).
Целая часть смешанного числа (mathbf{12frac{3}{8}}) меньше целой части смешанного числа (mathbf{13frac{1}{8}}).
Так как 12 < 13, то, (mathbf{color{orange}{12}frac{3}{8} < color{green}{13}frac{1}{8}}).
Смешанное число (mathbf{13frac{1}{8}}) соответствует неправильной дроби (mathbf{frac{105}{8}}).
В итоге получается следующий результат: (mathbf{12frac{3}{8} < frac{105}{8}})
При решении одного и того же задания разными способами, получили одинаковые ответы: сравнивая (mathbf{12frac{3}{8}}) и (mathbf{frac{105}{8}}) оказалось, что (mathbf{frac{105}{8}}) больше (mathbf{12frac{3}{8}}).
Эта информация доступна зарегистрированным пользователям
Смешанное число в развернутом виде представляет собой сумму целого и дробного числа.
При сложении смешанных чисел целые части складывают отдельно, дробные- отдельно.
Таким образом получается, что сложение смешанных чисел сводится к уже известным нам правилам сложения натуральных чисел и дробных чисел.
При сложении и вычитании можно использовать свойства, характерные для математических операций сложения и вычитания.
1. Запишем алгоритм сложения смешанных чисел.
Эта информация доступна зарегистрированным пользователям
- Сложить целые части смешанных чисел.
- Сложить дробные части смешанных чисел.
- Если при сложении дробных частей получается неправильная дробь, то из нее необходимо выделить целую часть и прибавить ее к уже найденной сумме в п.1.
Соблюдая данную логику, можно складывать любое количество смешанных чисел.
Разберем правило сложения смешанных чисел на примерах.
Пример №1.
Сложите два смешанных числа (mathbf{10frac{2}{5}}) и (mathbf{14frac{1}{5}}).
Решение:
Запишем первое и второе смешанное число в виде суммы целой и дробной части и сложим их, получим выражение вида: (mathbf{10 + frac{2}{5} + 14 + frac{1}{5}}).
Используя переместительное и сочетательное свойство сложения, сгруппируем отдельно целые части смешанных чисел, отдельно дробные части: (mathbf{(10 + 14) + (frac{2}{5} + frac{1}{5})}).
Выполним сложение двух натуральных чисел и сложение двух обыкновенных дробей с одинаковым знаменателем.
(mathbf{(10 + 14) + (frac{2}{5} + frac{1}{5}) = 24 + frac{2 + 1}{5} = 24 + frac{3}{5}})
Представим сумму (mathbf{24 + frac{3}{5}}) в виде смешанного числа:
(mathbf{24 + frac{3}{5} = 24frac{3}{5}})
В таком случае сумма двух смешанных чисел равна:
(mathbf{10frac{2}{5} + 14frac{1}{5} = 24frac{3}{5}})
Обычно все комментарии и рассуждения выполняются устно, а сложение и вычитание смешанных чисел оформляется в виде непрерывной цепочки действий:
(mathbf{10frac{2}{5} + 14frac{1}{5} = color{orange}{10} + color{green}{frac{2}{5}} + color{orange}{14} + color{green}{frac{1}{5}} = (color{orange}{10} + color{orange}{14}) + (color{green}{frac{2}{5}} + color{green}{frac{1}{5}}) = 24 + frac{2 + 1}{5} = 24 + frac{3}{5} = 24frac{3}{5}})
Пример №2.
Сложите два смешанных числа (mathbf{20frac{3}{5}}) и (mathbf{35frac{3}{5}}).
Решение:
Запишем первое и второе смешанное число в виде суммы целой и дробной части и сложим их, получим выражение вида: (mathbf{20 + frac{3}{5} + 35 + frac{3}{5}}).
Выполним сложение двух натуральных чисел и сложение двух обыкновенных дробей с одинаковым знаменателем: (mathbf{(20 + 35) + (frac{3}{5} + frac{3}{5}) = 55 + frac{6}{5}}).
При сложении дробных частей получаем неправильную дробь (mathbf{frac{6}{5}}).
Выделим из нее целую часть.
(mathbf{frac{6}{5} = 6 div 5 = 1frac{1}{5}})
Заменим неправильную дробь (mathbf{frac{6}{5}}) на соответствующее ей смешанное число (mathbf{1frac{1}{5}}).
Сложим целую часть полученного смешанного числа с уже имеющейся.
(mathbf{55 + color{blue}{frac{6}{5}} = 55 + color{blue}{1frac{1}{5}} = 55 + 1 + frac{1}{5} = (55 + 1) + frac{1}{5} = 56 + frac{1}{5} = 56frac{1}{5}})
Запишем решение в общем виде, опуская все комментарии и рассуждения:
(mathbf{20frac{3}{5} + 35frac{3}{5} = 20 + frac{3}{5} + 35 + frac{3}{5} = 55 + frac{6}{5} = 55 + 1frac{1}{5} = (55 + 1) + frac{1}{5} = 56 + frac{1}{5} = 56frac{1}{5}})
Пример №3.
Сложите два смешанных числа (mathbf{15frac{5}{7}}) и (mathbf{3frac{2}{7}}).
Решение:
(mathbf{15frac{5}{7} + 3frac{2}{7} = color{orange}{15} + color{green}{frac{5}{7}} + color{orange}{3} + color{green}{frac{2}{7}} = (color{orange}{15} + color{orange}{3}) + (color{green}{frac{5}{7}} + color{green}{frac{2}{7}}) = 18 + frac{7}{7} = 18 + 1 = 19})
При сложении двух смешанных чисел получили натуральное число.
2. Сложение смешанного числа и натурального числа.
Натуральное число можно представить в виде смешанного числа, дробная часть которого равна нулю.
В таком случае сумму смешанного числа и натурального числа находят как сумму двух смешанных чисел.
Так как дробная часть натурального числа равна нулю, то при сложении натурального и смешанного числа необходимо найти сумму только их целых частей, дробную же часть смешанного числа нужно оставить без изменений.
Пример.
Сложите два числа (mathbf{18frac{1}{3}}) и 4.
Решение:
(mathbf{18frac{1}{3} + 4 = color{orange}{18} + frac{1}{3} + color{orange}{4} = (color{orange}{18} + color{orange}{4}) + frac{1}{3} = 22 + frac{1}{3} = 22frac{1}{3}})
3. Сложение смешанного числа и обыкновенной дроби.
- Сложение смешанного числа и правильной дроби.
Правильную дробь можно представить в виде смешанного числа, целая часть которого равна нулю.
Если целая часть правильной дроби равна нулю, то складывая смешанное число и правильную дробь, находят только сумму дробной части смешанного числа и этой дроби, целую же часть смешанного числа при этом оставляют без изменений.
Пример.
Сложите два числа (mathbf{71frac{3}{10}}) и (mathbf{frac{1}{10}}).
Решение:
(mathbf{71frac{3}{10} + frac{1}{10} = 71 + color{green}{frac{3}{10}} + color{green}{frac{1}{10}} = 71 + (color{green}{frac{3}{10}} + color{green}{frac{1}{10}}) = 71 + frac{4}{10} = 71frac{4}{10}})
- Сложение смешанного числа и неправильной дроби
Возможны два способа сложение смешанного числа с неправильной дробью.
Первый способ: сложение смешанного числа и неправильной дроби можно свести к сумме двух неправильных дробей.
Для этого смешанное число можно представить в виде неправильной дроби и выполнить сложение неправильных дробей.
Второй способ: сложение смешанного числа и неправильной дроби можно свести к сумме двух смешанных чисел.
Для этого из неправильной дроби необходимо выделить целую часть и выполнить сложение двух смешанных чисел.
Рассмотрим несколько примеров.
Пример №1.
Сложите два числа (mathbf{3frac{1}{4}}) и (mathbf{frac{6}{4}}).
Решение:
Переведем неправильную дробь (mathbf{frac{6}{4}}) в смешанное число, разделив с остатком числитель на знаменатель дроби: 6 ÷ 4 = 1 (ост. 2), отсюда (mathbf{frac{6}{4} = 1frac{2}{4}}).
Подставим вместо (mathbf{frac{6}{4}}) соответствующее этой дроби смешанное число (mathbf{1frac{2}{4}}).
(mathbf{3frac{1}{4} + color{blue}{frac{6}{4}} = 3frac{1}{4} + color{blue}{1frac{2}{4}} = 3 + frac{1}{4} + 1 + frac{2}{4} = (3 + 1) + (frac{1}{4} +frac{2}{4}) = 4 + frac{3}{4} = 4frac{3}{4}})
Пример №2.
Сложите два числа (mathbf{3frac{1}{4}}) и (mathbf{frac{6}{4}}).
Решение:
Переведем смешанное число (mathbf{3frac{1}{4}}) в неправильную дробь.
Чтобы перевести смешанное число в неправильную дробь, необходимо умножить целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавить числитель дробной части, затем записать полученный результат суммы в числитель новой дроби, а знаменатель оставить без изменений.
(mathbf{3frac{1}{4} = frac{3 cdot 4 + 1}{4} = frac{13}{4}})
Подставим вместо смешанного числа (mathbf{3frac{1}{4}}) соответствующую ему неправильную дробь (mathbf{frac{13}{4}}).
(mathbf{color{blue}{3frac{1}{4}} + frac{6}{4} = color{blue}{frac{13}{4}} + frac{6}{4} = frac{13 + 6}{4} = frac{19}{4}})
Ответ запишем в виде смешанного числа, для этого из полученной неправильной дроби (mathbf{frac{19}{4}}) выделим целую часть: 19 ÷ 4 = 4 (ост. 3), следовательно, (mathbf{frac{19}{4} = 4frac{3}{4}})
Эта информация доступна зарегистрированным пользователям
Рассмотрим правила вычитания смешанных чисел.
В зависимости от того, какие значения принимают дробные части смешанных чисел, существуют различные варианты вычисления разности.
1. При вычитании смешанных чисел целые части вычитают отдельно, дробные- отдельно.
Вычитание одного смешанного числа из другого сводится к уже известным нам правилам вычитания натуральных чисел и вычитания дробных чисел.
Чтобы найти разность чисел, необходимо из уменьшаемого вычесть вычитаемое.
Запишем алгоритм вычитания смешанных чисел.
Эта информация доступна зарегистрированным пользователям
- Выполнить вычитание целых частей смешанных чисел.
- Выполнить вычитание дробных частей смешанных чисел.
- Сложить полученные результаты.
Сложнее ситуация будет складываться, если дробная часть уменьшаемого меньше дробной части вычитаемого.
В таком случае необходимо:
- Занять одну единицу от целой части уменьшаемого.
- Представить ее в виде дроби, в которой числитель равен знаменателю.
- Прибавить эту дробь к дробной части уменьшаемого.
- Выполнить вычитание целых частей смешанных чисел.
- Выполнить вычитание дробных частей смешанных чисел.
- Сложить полученные результаты.
Рассмотрим на примерах данные правила вычитания смешанных чисел.
Пример №1.
Вычислите разность двух смешанных чисел (mathbf{14frac{2}{5}}) и (mathbf{10frac{1}{5}}).
Решение:
Сравним дробные части смешанных чисел.
Для этого необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.
2– числитель дробной части уменьшаемого смешанного числа (mathbf{14frac{2}{5}}).
1– числитель дробной части вычитаемого смешанного числа (mathbf{10frac{1}{5}}).
Так как 2 > 1, значит (mathbf{frac{color{orange}{2}}{5} > frac{color{green}{1}}{5}})
Поскольку дробная часть уменьшаемого больше дробной части вычитаемого , выполним вычитание целых частей смешанных чисел, выполним вычитание дробных частей смешанных чисел, полученные результаты сложим.
(mathbf{14frac{2}{5} – 10frac{1}{5} = (color{orange}{14} + color{green}{frac{2}{5}}) – (color{orange}{10} + color{green}{frac{1}{5}}) = (color{orange}{14} – color{orange}{10}) + (color{green}{frac{2}{5}} – color{green}{frac{1}{5}}) = 4 + frac{2 – 1}{5} = 4 + frac{1}{5} = 4frac{1}{5}})
Пример №2.
Вычислите разность двух смешанных чисел (mathbf{31frac{2}{7}}) и (mathbf{1frac{4}{7}}).
Решение:
Сравним дробные части смешанных чисел.
Для этого необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.
2– числитель дробной части уменьшаемого смешанного числа (mathbf{31frac{2}{7}}).
4– числитель дробной части вычитаемого смешанного числа (mathbf{1frac{4}{7}}).
2 < 4, следовательно, (mathbf{frac{color{orange}{2}}{7} < frac{color{green}{4}}{7}})
Так как дробная часть уменьшаемого (mathbf{frac{2}{7}}) меньше дробной части вычитаемого (mathbf{frac{4}{7}}), займем единицу от целой части уменьшаемого и представим ее в виде дроби со знаменателем 7 (так как знаменатель всех имеющихся дробей в данном примере равен 7), уменьшив при этом целую часть уменьшаемого числа на единицу.
(mathbf{31frac{2}{7} – 1frac{4}{7} = (31 + frac{2}{7}) – (1 + frac{4}{7}) = (color{red}{31 – 1} + color{green}{1} + frac{2}{7}) – (1 + frac{4}{7}) =})
(mathbf{= (color{red}{30} + color{green}{frac{7}{7}} + frac{2}{7}) – (1 + frac{4}{7}) = (color{purple}{30} + color{blue}{frac{9}{7}}) – (color{purple}{1} + color{blue}{frac{4}{7}}) = (color{purple}{30} – color{purple}{1}) + (color{blue}{frac{9}{7}} – color{blue}{frac{4}{7}}) = 29 + frac{5}{7} = 29frac{5}{7}})
2. Вычитание смешанного числа из натурального числа.
При вычитании смешанного числа из натурального числа так же приходится занимать единицу от уменьшаемого натурального числа и представлять ее в виде дроби, в которой числитель равен знаменателю.
Рассмотрим поясняющий пример.
Вычислите разность чисел 20 и (mathbf{3frac{4}{5}}).
Решение:
Уменьшаемое число 20 не содержит дробную часть, займем у него единицу и представим ее в виде дроби со знаменателем 5 (так как знаменатель всех имеющихся дробей в данном примере равен 5), уменьшив при этом уменьшаемое натуральное число на единицу.
(mathbf{20 – 3frac{4}{5} = 20 – (3 + frac{4}{5}) = (color{red}{20 – 1} + color{green}{1}) – (3 + frac{4}{5}) = (color{red}{19} + color{green}{frac{5}{5}}) – (3 + frac{4}{5}) =})
(mathbf{= (19 – 3) + (frac{5}{5} – frac{4}{5}) = 16 + frac{1}{5} = 16frac{1}{5}})
3. Вычитание натурального числа из смешанного числа.
При вычитании из смешанного числа натурального числа необходимо вычесть из целой части смешанного числа натуральное число, оставив при этом дробную часть без изменений.
Пример.
Вычтем из смешанного числа (mathbf{15frac{1}{5}}) натуральное число 12.
(mathbf{15frac{1}{5} – 12 = (15 + frac{1}{5}) – 12 = (color{orange}{15} + frac{1}{5}) – color{orange}{12} = (color{orange}{15} – color{orange}{12}) + frac{1}{5} = 3frac{1}{5}})
4. Вычитание из смешанного числа обыкновенной дроби.
- Вычитание из смешанного числа правильной дроби.
При вычитании правильной дроби из смешанного числа необходимо вычесть дробь из дробной части этого смешанного числа, а целую часть его оставить неизменной.
Однако, если вычитаемая дробь больше чем дробная часть смешанного числа, то из его целой части придется занять единицу, представив ее в виде дроби, знаменатель которой равен числителю, целую часть смешанного числа при этом необходимо уменьшить на единицу.
Пример№ 1.
Найдите разность чисел (mathbf{19frac{7}{12}}) и (mathbf{frac{4}{12}}).
Решение:
Сравним числитель дробной части смешанного числа и вычитаемой дроби.
Числитель дроби (mathbf{frac{7}{12}}) равен 7.
Числитель дроби (mathbf{frac{4}{12}}) равен 4.
7 > 4, следовательно, (mathbf{frac{color{orange}{7}}{12} > frac{color{green}{4}}{12}}).
В таком случае действия просты, необходимо вычесть дробь из дробной части смешанного числа, а целую часть его оставить неизменной.
(mathbf{19frac{7}{12} – frac{4}{12} = (19 + color{green}{frac{7}{12}}) – color{green}{frac{4}{12}} = 19 + (color{green}{frac{7}{12}} – color{green}{frac{4}{12}}) = 19 + frac{3}{12} = 19frac{3}{12}})
Пример №2.
Найдите значение выражения (mathbf{8frac{7}{11} – frac{8}{11}}).
Решение:
Вычтем из смешанного числа (mathbf{8frac{7}{11}}) обыкновенную дробь (mathbf{frac{8}{11}}).
Сравним числители дробной части смешанного числа и вычитаемой дроби.
Числитель дроби (mathbf{frac{7}{11}}) равен 7.
Числитель дроби (mathbf{frac{8}{11}}) равен 8.
7 < 8, значит (mathbf{frac{color{orange}{7}}{11} < frac{color{green}{8}}{11}}).
Так как дробная часть уменьшаемого смешанного числа меньше вычитаемой дроби, займем единицу из целой части смешанного числа и представим ее в виде дроби со знаменателем 11 (так как знаменатель всех имеющихся дробей в данном примере равен 11), уменьшив при этом целую часть смешанного числа на единицу.
(mathbf{8frac{7}{11} – frac{8}{11} = (8 + frac{7}{11}) – frac{8}{11} = (color{red}{8 – 1} + color{green}{1} + frac{7}{11}) – frac{8}{11} = (color{red}{7} + color{green}{frac{11}{11}} + frac{7}{11}) – frac{8}{11} = })
(mathbf{= (7 + frac{18}{11}) – frac{8}{11} = 7 + (frac{18}{11} – frac{8}{11}) = 7 + frac{10}{11} = 7frac{10}{11}})
5. Вычитание из неправильной дроби смешанного числа.
Первый способ: вычитание смешанного числа из неправильной дроби и неправильной дроби из смешанного числа можно свести к разности двух неправильных дробей.
Для этого смешанное число можно представить в виде неправильной дроби и выполнить вычитание неправильных дробей.
Второй способ: вычитание смешанного числа из неправильной дроби и неправильной дроби из смешанного числа можно свести к разности двух смешанных чисел.
Для этого из неправильной дроби необходимо выделить целую часть и выполнить вычитание двух смешанных чисел.
Рассмотрим несколько примеров.
Пример №1.
Найдите значение выражения (mathbf{frac{122}{3} – 4frac{2}{3}}).
Решение:
Переведем неправильную дробь (mathbf{frac{122}{3}}) в смешанное число, разделив с остатком числитель на знаменатель дроби: 122 ÷ 3 = 40 (ост. 2), значит (mathbf{frac{122}{3} = 40frac{2}{3}}).
Подставим в исходное выражение вместо неправильной дроби (mathbf{frac{122}{3}}) соответствующее ему смешанное число (mathbf{40frac{2}{3}}).
Найдем разность двух смешанных чисел.
(mathbf{color{blue}{frac{122}{3}} – 4frac{2}{3} = color{blue}{40frac{2}{3}} – 4frac{2}{3} = (40 – 4) + (frac{2}{3} – frac{2}{3}) = 36 + 0 = 36})
Дробные части уменьшаемого и вычитаемого оказались равными, в итоге дробная часть оказалась равна нулю.
Пример №2.
Найдите значение выражения (mathbf{frac{21}{3} – 6frac{2}{3}}).
Решение:
Переведем (mathbf{6frac{2}{3}}) в неправильную дробь: (mathbf{6frac{2}{3} = frac{6 cdot 3 + 2}{3} = frac{20}{3}}).
Подставим в исходное выражение вместо смешанного числа (mathbf{6frac{2}{3}}) соответствующую ему неправильную дробь (mathbf{frac{20}{3}}).
Найдем разность двух неправильных дробей.
(mathbf{frac{21}{3} – color{blue}{6frac{2}{3}} = frac{21}{3} – color{blue}{frac{20}{3}} = frac{21 – 20}{3} = frac{1}{3}})
Эта информация доступна зарегистрированным пользователям
Арифметические операции сложения и вычитания часто используют при решении различных задач.
При решении задач арифметическим или алгебраическим способом используют основные свойства математических операций, применяют известные правила упрощения и преобразования выражений.
Часто одну и ту же текстовую задачу можно решить разными способами, отличающимися друг от друга логикой рассуждения.
Эта информация доступна зарегистрированным пользователям
Попробуем решить составную текстовую задачу на сложение и вычитание смешанных чисел.
Задача.
За три дня собрали (mathbf{17frac{2}{3}}) кг ягод.
В первый день собрали (mathbf{5frac{1}{3}}).
Во второй день собрали на (mathbf{frac{8}{3}}) кг больше, чем в первый день.
Сколько килограммов ягод собрали в третий день?
Эта информация доступна зарегистрированным пользователям
1. Решим данную задачу арифметическим способом (составлением выражения).
Запишем кратко условие задачи.
Собрали в первый день: (mathbf{5frac{1}{3}}) кг.
Собрали во второй день: (mathbf{5frac{1}{3} + frac{8}{3}}) кг.
Всего ягод собрали за три дня: (mathbf{17frac{2}{3}}) кг.
Собрали ягод на третий день- неизвестно.
Чтобы найти сколько ягод собрали на третий день необходимо из общего количества ягод, собранных за три дня, вычесть ягоды, собранные в первый и во второй день.
Составим выражение.
(mathbf{17frac{2}{3} – 5frac{1}{3} – (5frac{1}{3} + frac{8}{3})})
Найдем значение полученного выражения.
Данное выражение содержатся сразу несколько арифметических операций и скобки.
Определим порядок действий в данном выражении, используя правила, которые определяют порядок выполнения действий в математических выражениях.
1) Это выражение содержит скобки, поэтому выполним сначала действия в них.
Для этого найдем сумму смешанного числа и неправильной дроби.
Сложение смешанного числа и неправильной дроби можно свести к сумме двух смешанных чисел (из неправильной дроби необходимо выделить целую часть и выполнить сложение двух смешанных чисел).
Переведем неправильную дробь (mathbf{frac{8}{3}}) в смешанное число, разделив с остатком числитель на знаменатель дроби: 8 ÷ 3 = 2 (ост. 2), получаем (mathbf{frac{8}{3} = 2frac{2}{3}}).
(mathbf{5frac{1}{3} + color{blue}{frac{8}{3}} = 5frac{1}{3} + color{blue}{2frac{2}{3}} = color{purple}{5} + color{blue}{frac{1}{3}} + color{purple}{2} + color{blue}{frac{2}{3}} = (5 + 2) + (frac{1}{3} + frac{2}{3}) = 7 + frac{3}{3} = 7 + 1 = 8})
Так как оставшиеся за скобками действия- это действия первой ступени, то они выполняются по порядку слева направо.
2) Найдем разность смешанных чисел (mathbf{17frac{2}{3} – 5frac{1}{3}}).
Чтобы найти разность двух смешанных чисел, необходимо выполнить вычитание целых частей смешанных чисел, затем выполнить вычитание дробных частей этих чисел и сложить полученные результаты.
(mathbf{17frac{2}{3} – 5frac{1}{3} = (color{orange}{17} + color{green}{frac{2}{3}}) – (color{orange}{5} + color{green}{frac{1}{3}}) = (color{orange}{17} – color{orange}{5}) + (color{green}{frac{2}{3}} – color{green}{frac{1}{3}}) = 12 + frac{1}{3} = 12frac{1}{3}})
3) Найдем разность значений, полученных во втором и первом действии, т.е. из смешанного числа (mathbf{12frac{1}{3}}) вычтем натуральное число 8.
Чтобы вычесть из смешанного числа натуральное число, необходимо вычесть из целой части смешанного числа натуральное число, оставив при этом дробную часть без изменений.
(mathbf{12frac{1}{3} – 8 = color{orange}{12} + frac{1}{3} – color{orange}{8} = (color{orange}{12} – color{orange}{8}) + frac{1}{3} = 4 + frac{1}{3} = 4frac{1}{3}}) (кг) ягод собрали на третий день.
Ответ: (mathbf{4frac{1}{3}}) (кг).
Эту же задачу можно решить арифметическим способом, но по действиям.
Запишем кратко условие задачи.
Собрали в первый день: (mathbf{5frac{1}{3}}) кг.
Собрали во второй день: (mathbf{5frac{1}{3} + frac{8}{3}}) кг.
Всего ягод собрали за три дня: (mathbf{17frac{2}{3}}) кг.
Собрали ягод в третий день- неизвестно.
В таком случае решение данной задачи будет состоять из следующих этапов:
- первым делом найдем сколько ягод, собрали во второй день.
- далее, сложив полученный результат с ягодами, которые были собраны в первый день, найдем какое количество ягод собрали за первый и второй день.
- затем полученную сумму вычтем из общего количества ягод, собранных за три дня, в итоге получим сколько килограммов ягод, собрали за третий день.
1) (mathbf{5frac{1}{3} + color{blue}{frac{8}{3}} = 5frac{1}{3} + color{blue}{2frac{2}{3}} = color{purple}{5} + color{blue}{frac{1}{3}} + color{purple}{2} + color{blue}{frac{2}{3}} = (5 + 2) + (frac{1}{3} + frac{2}{3}) = 7 + frac{3}{3} = 7 + 1 = 8}) (кг) ягод собрали во второй день.
2) (mathbf{5frac{1}{3} + 8 = 5 + frac{1}{3} + 8 = (color{blue}{5} + color{blue}{8}) + frac{1}{3} = 13 + frac{1}{3} = 13frac{1}{3}}) (кг) ягод собрали за первый и второй день.
3) (mathbf{17frac{2}{3} – 13frac{1}{3} = (color{orange}{17} + color{green}{frac{2}{3}}) – (color{orange}{13} + color{green}{frac{1}{3}}) = (color{orange}{17} – color{orange}{13}) + (color{green}{frac{2}{3}} – color{green}{frac{1}{3}}) = 4frac{1}{3}}) (кг) ягод собрали на третий день.
Ответ: (mathbf{4frac{1}{3}}) (кг).
2. Решим задачу алгебраическим способом.
Кратко запишем условие задачи.
Собрали в первый день: (mathbf{5frac{1}{3}}) кг ягод.
Собрали во второй день: (mathbf{5frac{1}{3} + frac{8}{3}}) кг ягод.
Пусть х (кг) ягод собрали на третий день.
Зная, что всего собрали за три дня (mathbf{17frac{2}{3}}) кг ягод.
Составим уравнение.
(mathbf{5frac{1}{3} + (5frac{1}{3} + frac{8}{3}) + x = 17frac{2}{3}})
Упростим данное уравнение.
Выполним действие в скобках, т.е. найдем сумму смешанного числа (mathbf{5frac{1}{3}}) и неправильной дроби (mathbf{frac{8}{3}}), полученный результат сложим с первым слагаемым (mathbf{5frac{1}{3}}) (эти действия мы уже выполняли, решая задачу арифметическим способом).
(mathbf{5frac{1}{3} + frac{8}{3} = 5frac{1}{3} + 2frac{2}{3} = (5 + 2) + (frac{1}{3} + frac{2}{3}) = 7 + frac{3}{3} = 7 + 1 = 8})
(mathbf{5frac{1}{3} + 8 = 5 + frac{1}{3} + 8 = (5 + 8) + frac{1}{3} = 13 + frac{1}{3} = 13frac{1}{3}})
Получается, что выражение (mathbf{5frac{1}{3} + (5frac{1}{3} + frac{8}{3})}) тождественноравно выражению (mathbf{13frac{1}{3}}).
Подставим в исходное уравнение вместо суммы (mathbf{5frac{1}{3} + (5frac{1}{3} + frac{8}{3})}) смешанное число (mathbf{13frac{1}{3}}).
Получим простое уравнение с неизвестным слагаемым:
(mathbf{13frac{1}{3} + x = 17frac{2}{3}})
Чтобы найти неизвестное слагаемое, необходимо вычесть из суммы известное слагаемое.
(mathbf{13frac{1}{3} + x = 17frac{2}{3}})
(mathbf{x = 17frac{2}{3} – 13frac{1}{3}})
(mathbf{x = (17 + frac{2}{3}) – (13 + frac{1}{3})})
(mathbf{x = (17 – 13) + (frac{2}{3} – frac{1}{3})})
(mathbf{x = 4 + frac{1}{3}})
(mathbf{x = 4frac{1}{3}}) (кг) ягод собрали на третий день.
Ответ: (mathbf{4frac{1}{3}}) (кг).
Все три варианта решения задачи равноправны, дают одинаковый результат.
Эта информация доступна зарегистрированным пользователям
Читайте также
byesuca639
Вопрос по алгебре:
Найдите сумму целых частей чисел ;-3.8; 0.7 и 4.1.заранее спасибо
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
qunentipl210
Берёшь целые части и складываешь -4 + 0 + 4 = 0.
Ответ: 0
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

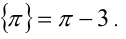
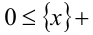
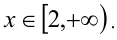
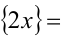
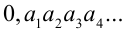
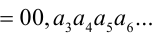
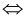
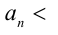
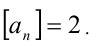
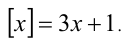
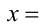
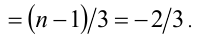
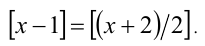
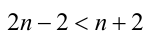
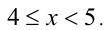
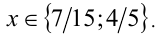
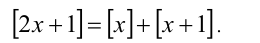
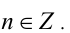
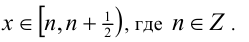
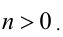
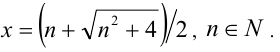
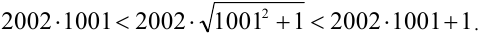
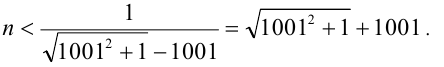
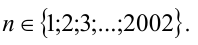


 , поэтому не знаю как быть)
, поэтому не знаю как быть)
