Как найти сумму цифр всех четырехзначных чисел

Содержание:

• 0.1 тЕЫЕОЙЕ
• 0.2 пФЧЕФ
• 0.3 йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
• 1 Другие интересные вопросы и ответы
  • 1.1 Какое среднее число между нулём и бесконечностью?

дБОЩ 6 ГЙЖТ: 0, 1, 2, 3, 4, 5. оБКФЙ УХННХ ЧУЕИ ЮЕФЩТЈИЪОБЮОЩИ ЮЈФОЩИ ЮЙУЕМ, ЛПФПТЩЕ НПЦОП ОБРЙУБФШ ЬФЙНЙ ГЙЖТБНЙ (ПДОБ Й ФБ ЦЕ ГЙЖТБ Ч ЮЙУМЕ НПЦЕФ РПЧФПТСФШУС).

тЕЫЕОЙЕ

вХДЕН ПФДЕМШОП РПДУЮЙФЩЧБФШ УХННХ ФЩУСЮ, УПФЕО, ДЕУСФЛПЧ Й ЕДЙОЙГ ДМС ТБУУНБФТЙЧБЕНЩИ ЮЙУЕМ. оБ РЕТЧПН НЕУФЕ НПЦЕФ УФПСФШ МАВБС ЙЪ РСФЙ ГЙЖТ 1, 2, 3, 4, 5. лПМЙЮЕУФЧП ЧУЕИ ЮЙУЕМ У ЖЙЛУЙТПЧБООПК РЕТЧПК ГЙЖТПК ТБЧОП 6·6·3 = 108, РПУЛПМШЛХ ОБ ЧФПТПН Й ФТЕФШЕН НЕУФЕ НПЦЕФ УФПСФШ МАВБС ЙЪ ЫЕУФЙ ГЙЖТ, Б ОБ ЮЕФЧЈТФПН НЕУФЕ – МАВБС ЙЪ ФТЈИ ГЙЖТ 0, 2, 4. рПЬФПНХ УХННБ ФЩУСЮ ТБЧОБ (1 + 2 + 3 + 4 + 5)·108·1000 = 1620000. лПМЙЮЕУФЧП ЮЙУЕМ У ЖЙЛУЙТПЧБООПК ЧФПТПК ГЙЖТПК ТБЧОП 6·3 = 90 (ОБ РЕТЧПН НЕУФЕ УФПЙФ МАВБС ЙЪ РСФЙ ГЙЖТ). рПЬФПНХ УХННБ УПФЕО ТБЧОБ
(1 + 2 + 3 + 4 + 5)·90·100 = 135000. бОБМПЗЙЮОП УХННБ ДЕУСФЛПЧ ТБЧОБ 13500, Б УХННБ ЕДЙОЙГ – (2 + 4)·5·6·6 = 1080.

пФЧЕФ

йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС

ПМЙНРЙБДБ
оБЪЧБОЙЕ	нПУЛПЧУЛБС НБФЕНБФЙЮЕУЛБС ПМЙНРЙБДБ
ЗПД
оПНЕТ	8
зПД	1945
ЧБТЙБОФ
лМБУУ	7,8
фХТ	2
ЪБДБЮБ
оПНЕТ	1

рТПЕЛФ ПУХЭЕУФЧМСЕФУС РТЙ РПДДЕТЦЛЕ Й .

Я не занимаюсь составлением программ и помнить формулы прогрессий тоже не в состоянии. Однако найти сумму всех трехзначных чисел не сложно. надо просто скомбинировать их правильным образом. Для начала отбросим число 100 и 550, которые пригодятся на последнем этапе подсчета. Потом обратим внимание, что 101+999 = 1100. Такая же сумма будет у всех остальных пар чисел до 549+551. Остается определить, сколько же пар чисел мы имеем 549-100 = 449. Теперь просто умножаем 449 на 1100, и добавляем к этому произведению отброшенные ранее числа 100 и 550. Получается 494550.

Только не надо путаться и добавлять 1000 – это уже четырехзначное число.

Другие интересные вопросы и ответы

Какое среднее число между нулём и бесконечностью?

Отвечу анекдотом: Поймали инопланетяне русского, американца и француза. И говорят: “Отпустим того, кто назовёт такое число, которого мы не знаем”. Американец подумал-подумал и говорит: “миллиард” Инопланетяне: “А, это мы знаем, столько планет в галактике” Француз подумал и говорит: “триллион” “А, ну это мы знаем. Столько звёзд на небе” Русский думает-думает и говорит: “дохрена” “Ого,- удивляются инопланетяне,- а это сколько?” “Ну вот вы приезжайте к нам в Россию, идите по железной дороге и считайте шпалы. Вот как только будет “да нахрен нам все это надо?” – так это и будет ровно половина”

У Вас недостаточно прав для добавления комментариев.
Вам необходимо зарегистрироваться на сайте

Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!

Размещения

№ 1. Имеем 4 разных конверта без марок и 3
разные марки. Сколькими способами можно выбрать
конверт и марку для отправления письма?

Решение:

34 = 12
(способов)

Ответ: 12 способов.

№ 2. В коробке находится 10 белых и 6 черных
шаров.

1) Сколькими способами из коробки можно вынуть
один шар любого цвета?

2) Сколькими способами из коробки можно вынуть
два разноцветных шара?

Решение:

= = = = 16 (способов)

= = 10

Ответ: 16; 60.

№ 3. В корзине лежат 12 яблок и 9 апельсинов (все
разные). Петя выбирает или яблоко, или апельсин,
после него из оставшихся фруктов Надя выбирает
яблоко и апельсин. Сколько возможно таких
выборов? При каком выборе Пети у Нади больше
возможностей выбора?

Решение:

+ = + = 21 + 19

Если Петя берёт 1 яблоко, то у Нади больше
возможностей для выбора.

Ответ: 401. Петя берёт 1 яблоко.

№ 4. Ученику необходимо сдать 4 экзамена на
протяжении 8 дней. Сколькими способами может быть
составлено расписание его экзаменов?

Решение:

= = = 5.

Ответ: 1680

№ 5. Сколькими способами может расположиться
семья из трех человек в четырехместном купе, если
других пассажиров в купе нет?

Решение:

= = . Ответ: 24.

№ 6. Из 30 участников собрания необходимо
выбрать председателя и секретаря. Сколькими
способами это можно сделать?

Решение:

= = = = = 29870(способов).

Ответ: 870.

№ 7. Сколькими способами могут занять первое,
второе и третье места 8 участниц финального
забега на дистанции 100 м?

Решение:

= = = = 6.

Ответ: 336.

№ 8. Сколькими способами можно изготовить
трехцветный флаг с горизонтальными полосами,
если есть материал 7 разных цветов?

Решение:

= = = = 5 = 210
(способов).

Ответ: 210.

№ 9. Сколькими способами организаторы
конкурса могут определить, кто из 15 его
участников будет выступать первым, вторым и
третьим?

Решение:

= = = =

= = =13 = 2780
(способов).

Ответ: 2780.

№ 10. На плоскости отметили 5 точек. Их
необходимо обозначить латинскими буквами.
Сколькими способами это можно сделать, если в
латинском алфавите 26 букв?

Решение:

= = = = 22 (способов)

Ответ: .

№ 11. Сколько четырехзначных чисел можно
составить из цифр 1, 3, 5, 7, 9,если цифры в числе не
повторяются?

Решение:

= = = 2 = 120
(способов).

Ответ: 120.

№ 12*. Сколько четырехзначных чисел можно
составить из цифр 0, 2, 4, 6, 8,если цифры в числе не
повторяются?

Решение:

= = – = 5! -4! = 4!(5 – 1)
= 1.

Ответ: 96.

№ 13. Сколько существует семизначных
телефонных номеров, в которых все цифры разные и
первая цифра отлична от нуля?

Решение:

= = – = – =

= 44 = 4  
(номеров)

Ответ: 544320.

№ 14. Сколько разных трехзначных чисел (без
повторения цифр) можно составить из цифр 1, 2, 3, 4, 5
так, чтобы полученные числа были: 1) четными; 2)
кратными 5?

Решение:

2= = = 2 2) = = = = 2

Ответ: 12; 48.

№ 15*. Решите уравнение: 1) =20; 2) = 6.

Решение:

=20;

= 20 ОДЗ: х

= 20

х² – х – 20 = 0

х₁=5, х₂= – 4(исключить).

Ответ: 5.

= 6.

= 6

= 6 ОДЗ: х

= 6

(х-4)(х-3) = 6

х² -3х -4х + 12 – 6 = 0

х² – 7х + 6 = 0 х₁ = 6, х₂ = 1
(исключить).

Ответ: 6.

Перестановки

№ 1. Сколькими способами 4 мужчины могут
расположиться на четырехместной скамейке?

Решение: Р₄ = 4! = 1 = 24 (способа)

Ответ: 24.

№ 2. Курьер должен разнести пакеты в 7 разных
учреждений. Сколько маршрутов он может выбрать?

Решение: Р₇ = 7! = 1

Ответ: 5040.

№ 3. Сколько существует выражений,
тождественно равных произведению abcde,
которые получаются из него перестановкой
множителей?

Решение: Р₅ = 5! =1 (выражений)

Ответ: 120.

№4. Ольга помнит, что телефон подруги
оканчивается тремя цифрами 5, 7, 8 но забыла, в
каком порядке эти цифры расположены. Укажите
наибольшее число вариантов, которые ей придется
перебрать, чтобы дозвониться подруге.

Решение:Р₃ = 3! = 1(вариантов)

Ответ: 6.

№ 5. Сколько шестизначных чисел (без
повторения цифр) можно составить из цифр:

1) 1, 2, 5, 6, 7, 8; 2) 0, 2, 5, 6, 7, 8?

Решение:

1) Р₆ = 1720.

2) Р₆ – Р₅ = 6! – 5! = 1

Ответ: 1) 720; 2) 600.

№ 6. Сколько среди четырехзначных чисел,
составленных из цифр 3, 5, 7, 9 (без повторения цифр),
есть такие, которые: 1) начинаются с цифры 3; 2)
кратны 5?

Решение:

1) Р₃ =3! = 1 2) Р₃ =3! = 1

Ответ: 1) 6; 2) 6.

№ 7. Найдите сумму цифр всех четырехзначных
чисел, которые можно составить из цифр 1, 3, 5, 7 (без
повторения цифр в числе).

Решение:

Р₄ = 4! = 1 = 24

1+3+5+7 = 16 16

Ответ: 384.

№ 8. В расписании на понедельник шесть уроков:
алгебра, геометрия, иностранный язык, история,
физкультура, химия. Сколькими способами можно
составить расписание уроков на этот день так,
чтобы два урока математики стояли подряд?

Решение:

2.

Ответ: 48.

№ 9*. Сколькими способами можно расставить на
полке 12 книг, из которых 5 книг — это сборники
стихотворений, чтобы сборники стихотворений
стояли рядом в случайном порядке?

Решение:

Р₇₅
= 7! 5! = 1

Ответ: 604800.

№ 10. Найдите, сколькими способами 5 мальчиков
и 5 девочек могут занять в театре в одном ряду
места с 1 по 10. Сколькими способами они могут это
сделать, если мальчики будут сидеть на нечетных
местах, а девочки — на четных?

Решение:

Р₁₀ = 10! =1 – расположения 5 мальчиков и 5 девочек в
любом месте и в любом ряду.

Если мальчики будут сидеть на нечетных местах,
а девочки — на четных, то таких способов будет
равно: Р₅₅
= 5!5! = 1

Ответ: 3628800; 14400.

Сочетания

№ 1. В классе 7-м учащихся успешно занимаются
математикой. Сколькими способами можно выбрать
из них двоих для участия в математической
олимпиаде?

Решение:  = = = = 21(способ).

Ответ: 21.

№ 2. В магазине “Филателия” продается 8
разных наборов марок, посвященных спортивной
тематике. Сколькими способами можно выбрать из
них 3 набора?

Решение:
= = = = 56
(способов).

Ответ: 56.

№ 3. Ученикам дали список из 10 книг, которые
рекомендуется прочитать во время каникул.
Сколькими способами ученик может выбрать из них 6
книг?

Решение:

= = = = 210
(способов).

Ответ: 210.

№ 4. На полке стоит 12 книг: англо-русский
словарь и 11 художественных произведений на
английском языке. Сколькими способами читатель
может выбрать 3 книги, если: 1) словарь ему нужен
обязательно; 2) словарь ему не нужен?

Решение: из 3 книг, которые надо выбрать – нужны
1 словарь и 2 художественные = Р₁ = 1! = 1 (способ) 2
художественные из 11 художественных можно
выбрать = = = = 55
(способов).

Тогда 1 словарь и 2 художественные книги можно
выбрать

= = = = 55 (способов)

Если не нужен словарь, то

= = = = 165
(способов).

Ответ: 55; 165.

№ 5. В классе учатся 16 мальчиков и 12 девочек.
Для уборки территории необходимо выделить
четырех мальчиков и трех девочек. Сколькими
способами это можно сделать?

Решение:

= = = = =
400400(способами)

Ответ: 400400.

Решите упражнения 6–26, используя известные
вам формулы и правила комбинаторики.

№ 6. Во время встречи 16 человек пожали друг
другу руки. Сколько всего сделано рукопожатий?

Решение:

= = = =
120(способов).

Ответ: 120.

№ 7. Группа учащихся из 30 человек решила
обменяться фотографиями.

Сколько всего фотографий необходимо было для
этого?

Решение:

= = = 870
(фотографий).

Ответ: 870.

№ 8. Сколько перестановок можно сделать из
букв слова “Харьков”?

Решение: Р₇ – Р₆ = 7! – 6! = 6!(7-1) = 6! = 1

Ответ: 4320.

№ 9. Бригадир должен откомандировать на
работу бригаду из 5 человек.

Сколько бригад по 5 человек в каждой можно
организовать из 12 человек?

Решение:

= = = = 3

Ответ: 3960.

№ 10. Сколькими разными способами собрание из
40 человек может выбрать из числа своих членов
председателя собрания, его заместителя и
секретаря?

Решение:

= = = = 59280
(способов)

Ответ: 59280.

№ 11. Сколько прямых линий можно провести
через 8 точек, из которых никакие три не лежат на
одной прямой?

Решение:
= = = = 28 (прямых
линий)

Ответ: 28.

№ 12. Сколько разных пятизначных чисел можно
записать с помощью цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 без их
повторения?

Решение:
= = = 2(разных
пятизначных числа)

Ответ: 126.

№ 13. Определите число всех диагоналей
правильного: 1) пятиугольника; 2) восьмиугольника;
3) двенадцатиугольника; 4) пятнадцатиугольника.

Решение: общая формула вычисления диагоналей у
n- угольника

= = = ;

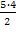1. n=5, то = 10
   (диагоналей)
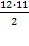2. n=12, то = 66
   (диагоналей)
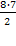3. n=8, то = 28
   (диагоналей)
4. n=15, то =
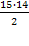   105(диагоналей)

Ответ: 10; 66; 28; 105.

№ 14. Сколько разных трехцветных флагов можно
сшить, комбинируя синий, красный и белый цвета?

Решение: Р₃ = 3! = 1 = 6 (флагов).

Ответ: 6.

№ 15. Сколько разных плоскостей можно
провести через 10 точек, если ни какие три из них
не лежат на одной прямой и никакие четыре точки
не лежат в одной плоскости?

Решение:  = = = 360 (разных
плоскостей)

Ответ: 360.

№ 16*. Сколько разных пятизначных чисел можно
записать с помощью цифр 0, 2, 4, 6, 8 без их
повторения?

Решение: Р₅ – Р₄ = 5! – 4! = 4! (5-1) = 4! 4 = 1 3 = 96 (разных
пятизначных чисел)

Ответ: 96.

№ 17. Среди перестановок из цифр 1, 2, 3, 4, 5
сколько таких, которые не начинаются цифрой 5?
числом 12? числом 123?

Решение: 4! = 1 3 –
перестановок начинаются цифрой 5.

3! = 1 3 6 –
перестановок начинаются цифрой 12.

2! = 1
перестановок начинаются с цифрами 123.

№ 18. Среди сочетаний из 10 букв a, b, c,
… по 4 сколько таких, которые не содержат буквы а?
букв a и b?

Решение:

1) – = – = – = – =

= = 63 (сочетаний
не содержат букву a)

2) ) – = – = – = – =

= = 140
(сочетаний не содержат букву a и b)

Ответ: 126; 140.

№ 19. Среди размещений из 12 букв a, b, c,
… по 5 сколько таких, которые не содержат буквы а?
букв a и b?

Решение:
– = – = – = =7 = 83160
(размещений)

– = – = – = =720(132 – 1) =
94320 (размещений)

Ответ: 83160; 94320.

№ 20. Сколько необходимо взять элементов,
чтобы число размещений из них по 4 было в 12 раз
больше, чем число размещений из них по 2?

Решение:
= 12 ОДЗ: х N;

x>4

= 12

(х-3)(х-2)(х-1)х = 12х(х-1)

(х-3)(х-2) = 12

х² -2х -3х +6 = 12

х² -5х – 6 = 0 =6, =-1

Ответ: 6.

Даны шесть цифр 0,1,2,3,4,5,6. Нужно найти сумму всех четырехзначных чётных чисел, которые можно написать этими цифрами (одна и та же цифра может повторяться).

Мое решение: Сначала я высчитал количество чисел, которые оканчиваются на нуль = 5^3. Остаются числа оканчивающиеся на 2 и 4. Их получается 5*6*6*2. Общее количество четырехзначных чётных чисел 5^3 + 5*6*6*2 = 485. То есть n = 485. Далее можно понять, что эти числа образуют арифметическую прогрессию с разностью 2, в которой первый член = 1000, а последний (наибольший чётный) = 5554, тогда несложно найти сумму = ((5554 + 1002)/)* 485 = 1589345, но этот ответ неверный.

Добавлено через 6 минут

((5554+1000)/2)*485 = 1589345

Добавлено через 4 минуты

Нашёл ошибку. Должно быть просто 5*6*6*3 = 540 и тогда всё верно