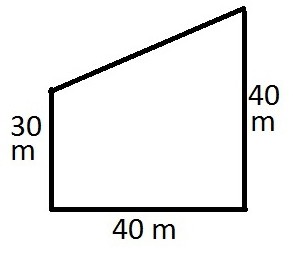
1. Формулы длины диагоналей прямоугольной трапеции по теореме Пифагора
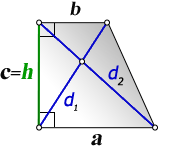
a – нижнее основание
b – верхнее основание
c=h – боковая сторона, равная высоте трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции:
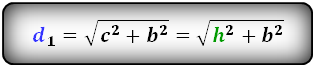
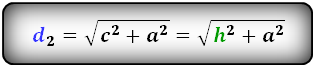
Остальные формулы диагоналей как для произвольной трапеции
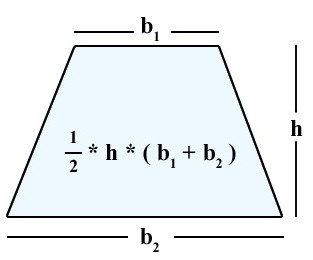
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
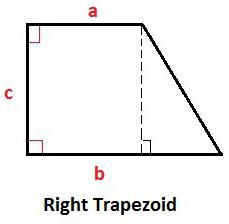
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
| Величина | Ее обозначение |
| a | большее основание |
| b | меньшее основание прямоугольной трапеции |
| c, h | перпендикулярная к основаниям боковая сторона, высота |
| d | наклонная боковая сторона |
| α | острый угол |
| β | тупой угол |
| м | средняя линия трапеции |
| д1 | меньшая диагональ |
| д2 | большая диагональ |
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
c = h.
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a – b) * tg α;
c = √ (d2 – (a – b)2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a – b) /cosα;
d = c / sin α;
d = √ (c2 + (а – b)2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с2 + b2)
или по-другому, заменив «с» на «h»:
d1 = √ (h2 + b2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с2 + b2) или d2 = √ (h2 + а2).
Задача №1
Условие. Площадь прямоугольной трапеции известна и равна 120 дм2. Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с2 + (а – b)2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а – b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2.
Необходимо сделать преобразования, подставив вместо с его значение из условия – 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см2.
Ответ. Искомая площадь 36 см2.
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
Особенности и свойства трапеций
Прежде чем разобраться, как найти площадь прямоугольной трапеции, следует подробнее рассмотреть свойства этого класса фигур. Все они представляют собой выпуклые четырехугольники, у которых две и всего две стороны параллельны между собой. Они называются основаниями и имеют разную длину. Оставшиеся две стороны наклонены друг относительно друга под определенным и неравным нулю углом. Они называются боковыми.
Нетрудно догадаться, что основания фигуры должны всегда отличаться по длине. В противном случае параллельными между собой окажутся также боковые стороны, и получится не трапеция, а прямоугольник или квадрат.
Терминология и элементы
Из определения трапеции следует, что эта фигура состоит из двух оснований и двух боковых сторон. Помимо них, в геометрии выделяют также следующие линейные характеристики:

- Диагонали — соединяющие несмежные (противоположные) вершины отрезки, в общем случае они имеют разную длину и могут быть вычислены из знания всех длин сторон фигуры. Соответствующие формулы имеют вид: D1 = (a*b + d 2 — a*(d 2 -c 2 )/(a-b))^0,5 и D2 = (a*b + c 2 — a*(c 2 -d 2 )/(a-b))^0,5. Здесь буквами a и b обозначены основания, c и d — это боковые стороны.
- Высота — расстояние между параллельными основаниями, она соответствует длине перпендикуляра, опущенного от малого основания к большому. Обычно ее обозначают буквой h. Через четыре стороны фигуры она так же, как и диагонали, может быть рассчитана. Соответствующая формула является несколько громоздкой. Она имеет вид: h = (4*(a-b)^2*d 2 — (d 2 + (a-b)^2 — c 2 )^2)^0,5/(2*(a-b)).
- Средняя линия или медиана M — отрезок, который соединяет середины сторон боковых, его длина однозначно рассчитывается из знания длин обоих оснований. Выражение для M имеет следующую форму: M = (a+b)/2 — полусумма длин оснований.
- В некоторых задачах также встречается отрезок n, который соединяет середины обеих диагоналей. Его длина рассчитывается как полуразница оснований: n = (a-b)/2.
Все формулы для нахождения длин соответствующих линейных элементов трапеции справедливы независимо от значений ее сторон и внутренних углов.
Существующие типы
Несмотря на простоту построения трапеции, она бывает нескольких типов. Последние определяются однозначно с учетом значения внутренних углов фигуры. В геометрии выделяют следующие типы:

- Общий. Этот тип фигуры является наименее симметричным. В ней все четыре угла отличаются друг от друга, при этом два из них являются тупыми, и два острыми. Их расположение может быть либо попарным, либо противоположным. Кроме того, трапеция общего типа имеет разные длины боковых сторон.
- Равнобедренный. Это самый симметричный тип фигуры. Равнобедренная трапеция по определению имеет две одинаковые по длине боковые стороны и, как следствие, равные попарно углы при основаниях (два острых и два тупых). Прямая, проходящая через середины оснований, является осью симметрии фигуры. Ее диагонали равны, а противоположные углы в сумме составляют 180 °. В такую трапецию можно вписать окружность, радиус которой составит половину высоты фигуры (r = h/2), однако, это не всегда возможно.
- Прямоугольный. Как следует из названия, для этого типа трапеции характерно наличие внутренних прямых углов, то есть таких, мера которых составляет 90 °. Поскольку сумма односторонних углов, заключенных между параллельными прямыми, всегда составляет 180 °, то в прямоугольной трапеции всегда существует два прямых угла. Два других угла являются острым и тупым.
Для всех перечисленных типов трапеции справедлив тот факт, что сумма четырех углов составляет 360 °. В любой тип фигуры можно вписать окружность. Для этого необходимо, чтобы выполнялось следующее условие:
a + b = c + d.
Другими словами, сумма длин оснований должна быть в точности равна сумме боковых сторон.
Прямоугольная фигура и ее характеристики
Несмотря на невысокую симметрию трапеции с прямыми углами, работать с ней удобно при решении задач, поскольку можно напрямую использовать теорему Пифагора.
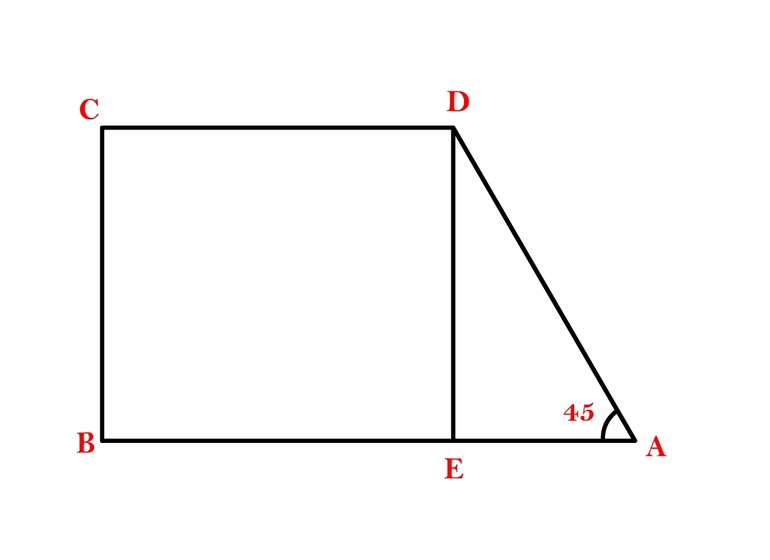
Пусть имеется фигура, в которой a и b — это основания, c — сторона, которая им обоим перпендикулярна и образует с ними прямые внутренние углы, d — боковая сторона, которая наклонена под некоторым углом к основаниям. Из такого построения ясно, что боковая сторона c также является высотой h фигуры.
Углы и диагонали
Формулы для расчета внутренних углов и длин диагоналей в прямоугольной фигуре имеют простой вид. Чтобы найти тупой и острый углы, достаточно рассмотреть прямоугольный треугольник, который образован следующими отрезками:
- перпендикуляром к основанию c;
- боковой стороной d;
- стороной a-b.
Нетрудно доказать, что синус острого угла α при основании может быть рассчитан по следующей формуле:
sin (α) = c/d.
Поскольку вместе с тупым углом β он составляет 180 °, тогда справедливы равенства:
sin (α) = sin (β) = c/d и β = 180 ° – α.
Для вычисления диагоналей прямоугольной трапеции можно воспользоваться общими формулами для D1 и D2.
Однако, для этого типа фигуры их можно упростить, воспользовавшись теоремой Пифагора. Любая из проведенных диагоналей образует внутри рассматриваемой трапеции прямоугольный треугольник, поэтому для D1 и D2 можно записать следующие равенства:
- D1 = (a 2 + c 2 )^0,5;
- D2 = (b 2 + c 2 )^0,5.
Для вычисления диагоналей D1 и D2 необязательно знать длину боковой стороны d.
Вычисление площади
Существует несколько выражений, используя которые можно определить площадь любой трапеции. Для прямоугольной фигуры все эти формулы имеют упрощенный вид. В первую очередь следует отметить общее выражение для площади S, которая равна произведению медианы M на высоту h:
S = M*h.
Для прямоугольной трапеции эта формула преобразуется в следующее равенство:
S = c*(a+b)/2.
Где h=c и M = (a+b)/2.
Удобно определять площадь рассматриваемой фигуры также через ее диагонали D1, D2 и угол их пересечения γ. Эта формула имеет вид:
S = D1*D2/2*sin (γ).
То есть половина произведения диагоналей на синус угла их пересечения дадут площадь всей фигуры. Необходимо отметить, что неважно, какой брать угол (острый или тупой) они связаны друг с другом (в сумме дают 180 °) и их синусы равны. Если диагонали пересекаются под прямым углом, то формула для S сводится к выражению:
S = D1*D2/2.
Существует еще одна формула площади трапеции прямоугольной через ее основания a, b и острый угол α. Применяя следующие рассуждения и выкладки можно ее получить:

- Следует рассмотреть прямоугольный треугольник, ограниченный отрезками c, b-a и d, где основание b больше, чем a.
- Высота c определяется следующей тригонометрической формулой: c = (b-a)*tg (α).
- Площадь фигуры рассчитывается из выражения общего типа: S = (b+a)*(b-a)*tg (α)/2. Эту формулу можно преобразовать таким образом: S = (b 2 — a 2 )*tg (α)/2.
Аналогичную формулу можно использовать, если известен не острый угол α, а тупой β. В этом случае выражение для S примет вид:
S = (a 2 -b 2 )*tg (β)/2.
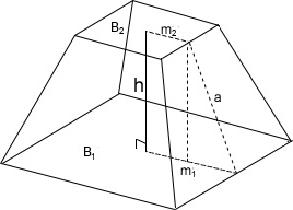
Функция tg (β) здесь является отрицательной величиной, поэтому вычитаемое и уменьшаемое в множителе a-b поменялись местами. Все выражения для расчета площади применимы при определении объема призм в трехмерном пространстве, у которых основания представляют собой трапеции.
Примеры решения задач
Пример 1. Пусть задана прямоугольная трапеция, медиана которой равна 12 см и острый угол при основании составляет 45 °. Также известно, что боковая сторона, которая не является высотой, составляет 10 см. Необходимо рассчитать площадь этой фигуры.
Если рассмотреть треугольник прямоугольный, который образован двумя боковыми сторонами и заданным острым углом, то можно рассчитать высоту фигуры:
h = d*sin (α) = 10*sin (45 °) = 7,071 см.
Поскольку из условия задачи известна медиана, то можно применить общую формулу для определения площади трапеции:
S = h*M = 7,071*12 = 84,852 см 2 .
Любопытно отметить, что для решения этой задачи не понадобилось знать длины каждого из оснований.
Пример 2. Известно, что большее из оснований трапеции прямоугольной имеет длину 12 см, ее наклонная сторона равна 10 см, а угол при основании составляет 53,13 °. Необходимо выяснить, как найти площадь прямоугольной трапеции из этих данных.
Для решения задачи удобно использовать следующие общепринятые обозначения:
- α = 53,13 °;
- b = 12 см;
- d = 10 см.
Рассматривая треугольник с прямым углом, который заключен между сторонами b-a, d и c, можно вычислить все неизвестные длины отрезков:
- c = d*sin (α);
- b-a = d*cos (α), откуда a = b — d*cos (α).
Общая формула для площади трапеции приобретает вид:
S = M*h = (a+b)/2*c = (2*b — d*cos (α))*d*sin (α)/2.
Все величины в формуле известны из условия задачи. Если их подставить, то получится ответ: 72 см2.
Пример 3. Известно, что в трапеции с прямыми углами диагонали составляют 7 см и 11 см, высота фигуры равна 5 см. Необходимо найти ее площадь.

Из теоремы Пифагора следует, что каждое из оснований трапеции может быть вычислено следующим образом:
- a = (D1 2 -c 2 )^0,5 = (49−25)^0,5 = 4,9 см;
- b = (D2 2 -c 2 )^0,5 = (121−25)^0,5 = 9,8 см.
Тогда площадь фигуры составит: S = (a+b)*c/2 = (4,9+9,8)*5/2 = 36,75 см2.
Таким образом, прямоугольная трапеция является простой фигурой, для вычисления площади которой удобно воспользоваться теоремой Пифагора. Существуют несколько формул для определения величины S, параметрами которых являются длины сторон и непрямые углы.
В данной публикации мы рассмотрим определение и основные свойства прямоугольной трапеции.
Напомним, трапеция называется прямоугольной, если углы при одной из ее боковых сторон прямые, т.е. равняются 90°.

- Свойство 1
- Свойство 2
- Свойство 3
-
Свойство 4
Свойство 1
Два угла прямоугольной трапеции обязательно являются прямыми, принадлежат одной боковой стороне, а вершины данных углов – смежные.
Для рисунка выше:
- ∠BAD = ∠ABC = α = 90°
- ∠BAD и ∠ABC принадлежат боковой стороне AB
- Вершины A и B – смежные.
Свойство 2
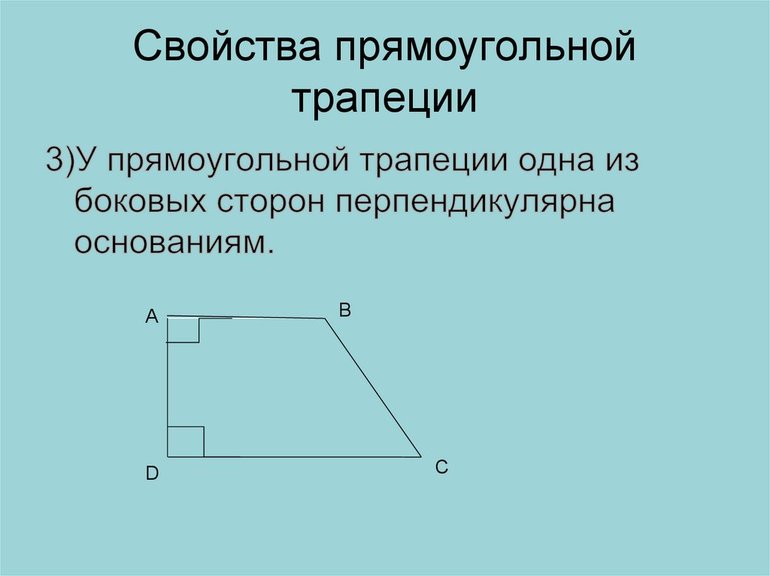
Одна из боковых сторон прямоугольной трапеции перпендикулярна ее основаниям.
На рисунке выше: AB ⊥ AD и AB ⊥ BC.
Свойство 3
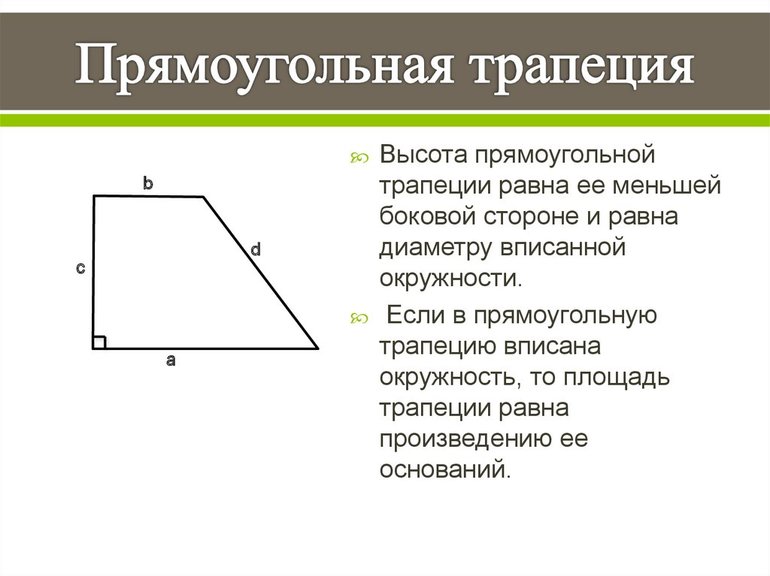
Высота прямоугольной трапеции (h) совпадает с меньшей боковой стороной (AB), перпендикулярной основаниям.

Свойство 4
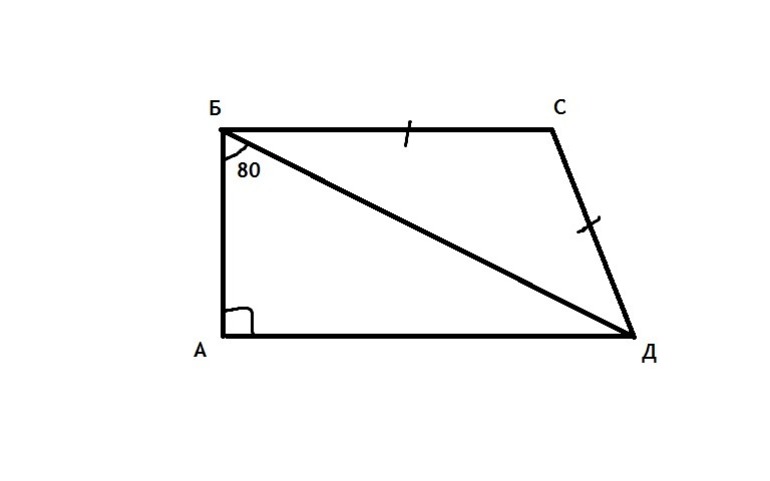
Каждая из диагоналей прямоугольной трапеции делит ее на два треугольника, один из которых, также, является прямоугольным.

- Диагональ AC делит трапецию на треугольники ABC и ACD, причем ΔABC является прямоугольным с прямым углом в вершине B.
- Диагональ BD делит трапецию на ΔABD (прямоугольный) и ΔBCD.
Примечание: остальные свойства, которые применимы ко всем видам трапеций, приведены в нашей публикации – “Что такое трапеция: определение, виды, свойства”.
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
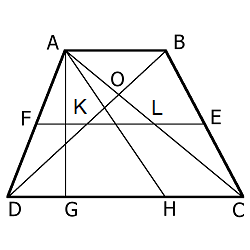
-
Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме
$$
FE = {AB + DC over 2}
$$ -
Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
-
Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е.
$$
KL = {DC – AB over 2}
$$ - Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции

- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции

Площадь трапеции через основания и высоту
$$
S = {AB + DC over 2} * AG
$$
Площадь трапеции через среднюю линию и высоту
$$
S = FE * AG
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC * BD over 2} * sin(∠AOD) = {AC * BD over 2} * sin(∠AOB)
$$
Площадь трапеции через четыре стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 – ({(DC – AB)^2 + AD^2 – BC^2 over 2 * (DC – AB)})^2}
$$
Формулы площади равнобедренной трапеции


Площадь трапеции через стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 – {(DC – AB)^2 over 4}}
$$
Площадь трапеции через стороны и угол
$$
S = AD * sin(∠ADC) * (DC – AD * cos(∠ADC))
$$
$$
S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC))
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC^2 over 2} * sin(∠AOD) = {AC^2 over 2} * sin(∠BOC)
$$
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$
S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB)
$$
Площадь трапеции если в нее вписана окружность
$$
S = {4 * R_В^2 over sin(∠ADC)} = {4 * R_В^2 over sin(∠DAB)}
$$
$$
S = {AB * DC over sin(∠ADC)} = {AB * DC over sin(∠DAB)}
$$
Формулы сторон произвольной трапеции

Основание через другое основание и среднюю линию
$$
AB = 2 * FE – DC
$$
$$
DC = 2 * FE – AB
$$
Основание через другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AG} * sin(∠AOD) – AB
$$
$$
AB = {AC * BD over AG} * sin(∠AOD) – DC
$$
Длины сторон
$$
DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
AB = DC – AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD)
$$
$$
AB = DC – AD * cos(∠ADC) – BC * cos(∠BCD)
$$
$$
AD = {AG over sin(∠ADC)}
$$
$$
BC = {AG over sin(∠BCD)}
$$
Формулы сторон равнобедренной трапеции


Длины сторон
$$
AD = {AG over sin(∠ADC)}
$$
$$
AD = {DC – AB over 2 * cos(∠ADC)}
$$
$$
DC = AB + 2 * AG * ctg(∠ADC)
$$
$$
AB = DC – 2 * AG * ctg(∠ADC)
$$
$$
DC = AB + 2 * AB * cos(∠ADC)
$$
$$
AB = DC – 2 * AB * cos(∠ADC)
$$
Длина основания через диагональ, боковую сторону и другое основание
$$
DC = {AC^2 – DA^2 over AB}
$$
$$
AB = {AC^2 – DA^2 over DC}
$$
Длина боковой стороны через диагональ и основания
$$
AD = sqrt{AC^2 – AB * DC}
$$
Длина основания через высоту, другое основание, диагонали и угол между ними
$$
DC = {AC^2 over AG} * sin(∠AOD) – AB
$$
$$
AB = {AC^2 over AG} * sin(∠AOD) – DC
$$
Длина основания через высоту, другое основание и площадь трапеции
$$
DC = {2 * S over AG} – AB
$$
$$
AB = {2 * S over AG} – DC
$$
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
$$
AD = {S over FE * sin(∠ADC)} = {S over FE * sin(∠DAB)}
$$
Длина боковой стороны через площадь трапеции, основания и угол при основании
$$
AD = {2 * S over (AB + DC) * sin(∠ADC)}
$$
$$
AD = {2 * S over (AB + DC) * sin(∠DAB)}
$$
Формулы сторон прямоугольной трапеции

Длины оснований
$$
DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD)
$$
$$
AB = DC – BC * cos(∠BCD) = DC – AD * ctg(∠BCD)
$$
$$
DC = AB + sqrt{BC^2 – AD^2}
$$
$$
AB = DC – sqrt{BC^2 – AD^2}
$$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AD} * sin(∠AOD) – AB
$$
$$
AB = {AC * BD over AD} * sin(∠AOD) – DC
$$
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG)
$$
DC = {2 * S over AD} – AB
$$
$$
AB = {2 * S over AD} – DC
$$
Формулы диагоналей произвольной трапеции

Длина диагоналей через четыре стороны
$$
BD = sqrt{BC^2 + DC * AB – {DC * (BC^2 – AD^2) over DC – AB}}
$$
$$
AC = sqrt{AD^2 + DC * AB – {DC * (AD^2 – BC^2) over DC – AB}}
$$
Длина диагоналей по теореме косинусов
$$
BD = sqrt{DC^2 + BC^2 – 2 * DC * BC * cos(∠BCD)}
$$
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * AD * cos(∠ADC)}
$$
Длина диагоналей через высоту
$$
BD = sqrt{AG^2 + (DC – AG * ctg(∠BCD))^2}
$$
$$
BD = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
$$
BD = sqrt{DC^2 + BC^2 – 2 * DC * sqrt{BC^2 – AG^2}}
$$
$$
AC = sqrt{AG^2 + (DC – AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠BCD))^2}
$$
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * sqrt{AD^2 – AG^2}}
$$
Длина диагоналей через стороны и другую диагональ
$$
BD = sqrt{AD^2 + BC^2 + 2 * DC * AB – AC^2}
$$
$$
AC = sqrt{AD^2 + BC^2 + 2 * DC * AB – BD^2}
$$
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
$$
BD = {AG * (DC + AB) over AC * sin(∠AOD)}
$$
$$
AC = {AG * (DC + AB) over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
$$
BD = {2 * S over AC * sin(∠AOD)}
$$
$$
AC = {2 * S over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
$$
BD = {2 * FE * AG over AC * sin(∠AOD)}
$$
$$
AC = {2 * FE * AG over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Формулы диагоналей равнобедренной трапеции


Длина диагоналей через стороны
$$
AC = sqrt{AD^2 + AB * DC}
$$
Длина диагоналей по теореме косинусов
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * AD * cos(∠ADC)}
$$
$$
AC = sqrt{DC^2 + AD^2 + 2 * DC * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 – 2 * AB * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 + 2 * AB * AD * cos(∠ADC)}
$$
Длина диагоналей
$$
AC = sqrt{AG^2 + FE^2}
$$
$$
AC = sqrt{AG^2 + {(DC + AB)^2 over 4 }}
$$
$$
AC = sqrt{{AG * (AB + DC) over sin(∠AOD)}} = sqrt{{2 * S over sin(∠AOD)}} = sqrt{{2 * FE * AG over sin(∠AOD)}}
$$
Длина диагоналей через высоту основание и угол при основании
$$
AC = sqrt{AG^2 + (DC – AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
Длина диагоналей через сторону и высоту
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * sqrt{AD^2 – AG^2}}
$$
Формулы диагоналей прямоугольной трапеции

$$
BD = sqrt{AD^2 + AB^2}
$$
$$
AC = sqrt{AC^2 + DC^2}
$$
Формулы средней линии произвольной трапеции

Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC – AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и высоту
$$
FE = {S over AG}
$$
Формулы средней линии равнобедренной трапеции


Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC – AG * ctg(∠ADC) = AB + AG * ctg(∠ADC)
$$
Длина средней линии через основания, боковую сторону и высоту
$$
FE = DC – sqrt{AD^2 – AG^2} = AB + sqrt{AD^2 – AG^2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC^2 over 2 * AG} * sin(∠AOD) = {AC^2 over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и боковую сторону
$$
FE = {S over AD * sin(∠ADC)}
$$
Формулы средней линии прямоугольной трапеции

Длина средней линии через основания, высоту и угол при нижнем основании
$$
FE = DC – AG * {ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠BCD) over 2}
$$
Длина средней линии через основания, боковую сторону и угол при нижнем основании
$$
FE = DC – BC * {cos(∠BCD) over 2}
$$
$$
FE = AB + BC * {cos(∠BCD) over 2}
$$
Длина средней линии через основания и боковые стороны
$$
FE = DC – {sqrt{BC^2 – AD^2} over 2}
$$
$$
FE = AB + {sqrt{BC^2 – AD^2} over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Формулы высоты произвольной трапеции

Длина высоты через четыре стороны
$$
AG = sqrt{AD^2 – ({(DC – AB)^2 + AD^2 – BC^2 over 2 * (DC – AB)})^2}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC) = BC * sin(∠BCD)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC * BD over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC * BD over AB + DC} * sin(∠AOB)
$$
Длина высоты через среднюю линию, диагонали и углы между ними
$$
AG = {AC * BD over 2 * FE} * sin(∠AOD)
$$
$$
AG = {AC * BD over 2 * FE} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы высоты равнобедренной трапеции


Длина высоты через по сторонам
$$
AG = sqrt{AD^2 – {(DC – AB)^2 over 4}}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC)
$$
Длина высоты через основания и прилегающий угол к основанию
$$
AG = {DC – AB over 2} * tg(∠ADC)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC^2 over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC^2 over AB + DC} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы боковых сторон прямоугольной трапеции

Сторона AD
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
$$
BC = sqrt{AD^2 + (DC – AB)^2}
$$
Сторона BC через основания и угол ∠BCD
$$
BC = {DC – AB over cos(∠BCD)}
$$
Сторона BC через Сторону AD
$$
BC = {AD over sin(∠BCD)}
$$
Сторона BC через площадь, среднюю линию и угол ∠BCD
$$
BC = {S over FE * sin(∠BCD)}
$$
Сторона BC через площадь, основания и угол ∠BCD
$$
BC = {2 * S over (AB + DC) * sin(∠BCD)}
$$
