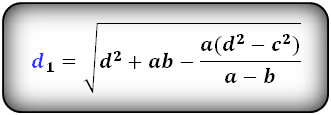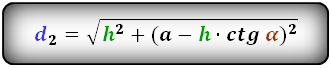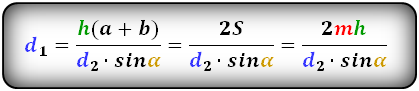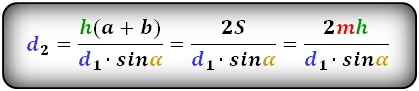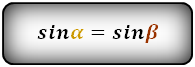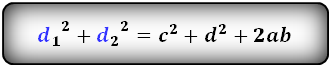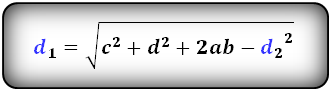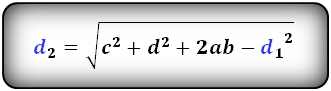Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
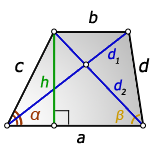
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
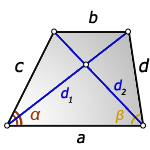
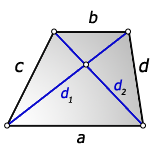
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
d1 , d2 – диагонали трапеции
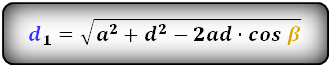
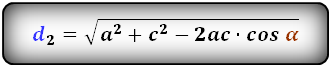
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
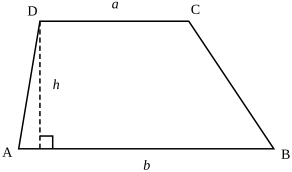
2. Формула длины диагоналей трапеции через высоту
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции через высоту:
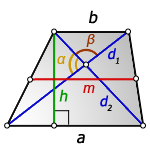
3. Формула длины диагонали трапеции через другую диагональ
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d1 , d2 – диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 23 октября 2013
-
Обновлено: 13 августа 2021
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m – b
b = 2m – a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 – 2ad·cos β
d2 = √a2 + c2 – 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab – | a(d 2 – c2) |
| a – b |
| d2 = | √ | c2 + ab – | a(c2 – d 2) |
| a – b |
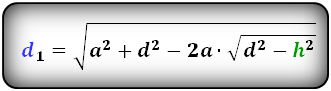
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a – h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a – h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab – d22
d2 = √c2 + d 2 + 2ab – d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 – | ( | (a – b)2 + c2 – d 2 | ) | 2 |
| 2 | 2(a – b) |
5. Формула Герона для трапеции
| S = | a + b | √(p – a)(p – b)(p – a – c)(p – a – d) |
| |a – b| |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2022 года; проверки требуют 27 правок.
Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол») — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны[1]. Часто в определении трапеции опускают последнее условие (см. ниже). Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.
Варианты определения
Существует и другое определение трапеции.
Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны[2][3]. Согласно этому определению, параллелограмм и прямоугольник — частные случаи трапеции. Однако при использовании такого определения большинство признаков и свойств равнобедренной трапеции перестают быть верными (так как параллелограмм становится её частным случаем). Приведённые в разделе Общие свойства формулы верны для обоих определений трапеции.
Связанные определения
Элементы трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Параллельные противоположные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Углом при основании трапеции называется её внутренний угол, образованный основанием с боковой стороной.
Виды трапеций
- Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой[4] или равнобочной[5] трапецией).
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
-
Равнобедренная трапеция
-
Прямоугольная трапеция
Свойства
Основной источник: [6]
- Сумма углов, прилежащих к боковой стороне трапеции, равна
(как сумма двух внутренних односторонних углов при параллельных прямых, содержащих основания трапеции, и секущей, содержащей боковую сторону).
- Средняя линия трапеции параллельна основаниям и равна их полусумме.[7]
- Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен
среднему гармоническому длин оснований трапеции.
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
- Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
- Диагонали трапеции делят её на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, являются равновеликими [имеют одинаковую площадь].
- Если отношение оснований равно
, то отношение площадей треугольников, прилежащих к основаниям, равно
.
- Высота трапеции определяется формулой:
-
- где
— большее основание,
— меньшее основание,
и
— боковые стороны.
-
- Их можно выразить в явном виде:
- Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:
- а при известных основаниях и диагоналях боковые стороны следующие:
- Если же известна высота
, то
- Прямая Ньютона для трапеции совпадает с её средней линией.
Неравенства для отрезков в трапеции
Теорема о четырёх точках трапеции
Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.
Равнобедренная трапеция
Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:
- прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции)[8];
- высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
- углы при любом основании равны;
- сумма противоположных углов равна 180°;
- длины диагоналей равны;
- диагонали трапеции образовывали с одним и тем же основание равные углы;
- из каждой вершины одного основания другое основание было видно под одним и тем же углом[9];
- вокруг этой трапеции можно описать окружность;
- вершинами этой трапеции также являются вершины некоторого антипараллелограмма.
Кроме того
- если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Если 




Вписанная и описанная окружность
- Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
- В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
- Если трапецию можно вписать в окружность — то она равнобедренная.
- Радиус описанной окружности равнобедренной трапеции:[источник не указан 2873 дня]
-
- где
— боковая сторона,
— бо́льшее основание,
— меньшее основание,
— диагонали равнобедренной трапеции.
- Если
, то в равнобедренную трапецию можно вписать окружность радиуса
Площадь
- Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.
Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:
-
- или
- Средняя линия
разбивает фигуру на две трапеции, площади которых соотносятся как[11]
- Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
Формулы площади равнобедренной трапеции
- Площадь равнобедренной трапеции:
-
- где
— боковая сторона,
— бо́льшее основание,
— меньшее основание,
— угол между бо́льшим основанием и боковой стороной[12].
- Площадь равнобедренной трапеции через её стороны
- Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты:
В этом случае средняя линия совпадает по длине с высотой трапеции, т. е. 
История
Слово «трапеция» происходит от греческого слова др.-греч. τραπέζιον «столик» (уменьш. от τράπεζα «стол»), означающего стол. В русском языке от этого слова происходит слово «трапеза» (еда).
Примечания
- ↑ Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 587.
- ↑ Вся элементарная математика. Дата обращения: 6 июля 2015. Архивировано 9 июля 2015 года.
- ↑ Wolfram MathWorld. Дата обращения: 6 июля 2015. Архивировано 19 апреля 2015 года.
- ↑ Коллектив авторов. Современный справочник школьника. 5-11 классы. Все предметы. — Litres, 2015-09-03. — С. 82. — 482 с. — ISBN 9785457410022.
- ↑ М. И. Сканави. Элементарная математика. — 2013. — С. 437. — 611 с. — ISBN 9785458254489.
- ↑ Четырёхугольники. Архивная копия от 16 сентября 2015 на Wayback Machine
- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 99.
- ↑ Эквивалентная формулировка: отрезки, соединяющие середины противоположных сторон трапеции, были взаимно перпендикулярны.
- ↑ Следствие. В случае перпендикулярности диагоналей боковым сторонам трапеция является равнобедренной.
- ↑ Комарова В. В. Экзаменационные вопросы и ответы. Геометрия: 9 и 11 выпускные классы. — М.: АСТ-ПРЕСС, 2000. — 448 с. — ISBN 5-7805-0416-4.
- ↑ Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. 2-е изд., перераб. и доп. — М.: Наука, 1974. — 592 с.
- ↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов 1986. С. 184
Все формулы диагоналей трапеции
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d 1 , d 2 – диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны :
2. Формула длины диагоналей трапеции через высоту
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
h – высота трапеции
d 1 , d 2 – диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
a – нижнее основание
b – верхнее основание
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d 1 , d 2 – диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d 1 , d 2 – диагонали трапеции
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a – h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a – c· cos α – d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 – 2 ad· cos β
d 2 = √ a 2 + c 2 – 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab – | a ( d 2 – c 2 ) |
| a – b |
| d 2 = | √ | c 2 + ab – | a ( c 2 – d 2 ) |
| a – b |
d 1 = √ h 2 + ( a – h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a – h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab – d 2 2
d 2 = √ c 2 + d 2 + 2 ab – d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 – | ( | ( a – b ) 2 + c 2 – d 2 | ) | 2 |
| 2 | 2( a – b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p – a )( p – b )( p – a – c )( p – a – d ) |
| | a – b | |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Диагонали трапеции
Свойства диагоналей трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения – подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции – равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b – основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Свойства треугольников, образованных диагоналями трапеции
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Свойства трапеции, достроенной до треугольника
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Свойства отрезка, параллельного основаниям трапеции
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Формулы нахождения диагоналей трапеции через высоту
Примечание. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа – задайте вопрос на форуме.
Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам – AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Задача .
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение .
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая – то обозначим длину AM = a, длину KD = b ( не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK – прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 – b
Треугольники DBM и ACK – прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
h 2 + (24 – a) 2 = (5√17) 2
и
h 2 + (24 – b) 2 = 13 2
Учтем, что a = 16 – b , тогда в первом уравнении
h 2 + (24 – 16 + b) 2 = 425
h 2 = 425 – (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 – (8 + b) 2 + (24 – b) 2 = 169
-(64 + 16b + b) 2 + (24 – b) 2 = -256
-64 – 16b – b 2 + 576 – 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 – (8 + b) 2 = 425 – (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b – основания трапеции, h – высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ: площадь трапеции равна 80 см 2 .
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/formula/trapezium/
http://profmeter.com.ua/communication/learning/course/course7/lesson181/
[/spoiler]
Свойства трапеции
Итак, что ты должен знать о свойствах трапеции…
Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))
Почему так?
Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая.
Вот и получается, что ( displaystyle angle 1) и ( displaystyle angle 2) – внутренние односторонние углы при параллельных ( displaystyle AD) и ( displaystyle BC) и секущей ( displaystyle AB).
Поэтому ( displaystyle angle 1+angle 2=180{}^circ ).
И точно так же ( displaystyle angle 3) и ( displaystyle angle 4) – внутренние односторонние углы при тех же параллельных ( displaystyle AD) и ( displaystyle BC), но секущая теперь – ( displaystyle CD).
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
Снова порассуждаем об углах:
Опять ( displaystyle AD) и ( displaystyle BC) – параллельные, а диагональ ( displaystyle AC) – секущая. Поэтому ( displaystyle angle 1=angle 2).
А теперь рассмотрим сразу 2 диагонали и 4 угла:
( displaystyle angle 1=angle 2)
( displaystyle angle 3=angle 4)
Что из этого может следовать?
Очень важный факт:
Треугольники ( displaystyle BOC) и ( displaystyle AOD) – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: ( displaystyle K=frac{a}{b}).