Математика, 2 класс. Урок №13.
Длина ломаной. Закрепление
Перечень вопросов, рассматриваемых в теме:
– Как найти длину ломаной?
Глоссарий по теме:
Ломаная – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.
Звенья – отрезки, из которых состоит ломаная.
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
Длина ломаной – это сумма длин всех её звеньев.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35
2. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017 – с.20, 21
3. Математика. Тесты. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017 – с.20, 21, 25
Теоретический материал для самостоятельного изучения
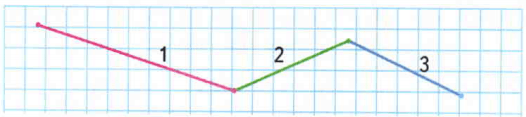
На рисунке мы видим ломаную линию, состоящую из трёх звеньев.
Как найти длину ломаной линии? Это можно сделать двумя способами.
Первый способ. Сначала узнаем длину каждого звена с помощью линейки
Длина первого звена 4 см.
Длина второго звена 6 см.
Длина третьего звена 5 см.
Найдем сумму этих длин.
4+6+5=15 (см)
Найдем длину ломаной вторым способом.
Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.
Накладываем циркуль на второй отрезок, переносим его на прямую.
Накладываем циркуль на третий отрезок, переносим его на прямую.
Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.
Выводы: длину ломаной можно находить двумя способами.
Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.
Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка. Это и будет длина всей ломаной.
Тренировочные задания.
1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см
Варианты ответов:
10 см 8 см 7 см
Правильный вариант:
10 см 8 см 7 см
2. Расположите ломаные линии по порядку: от самой короткой до самой длинной
Правильный вариант: Найдем длину каждой ломаной
6 + 2 + 2 = 10 см
7 + 5 = 12 см
2 + 1 + 3 +2 = 8 см
3 + 1 + 5 = 9 см
Расставим в порядке возрастания:
2 + 1 + 3 + 2 = 8 см
3 + 1 + 5 = 9 см
6 + 2 + 2 = 10 см
7 + 5 = 12 см
Ломаная линия
- Замкнутая и незамкнутая ломаная
- Самопересекающаяся ломаная
- Длина ломаной
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE
или ломаная EDCBA
.
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:
многоугольник ABCDE.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Ответ: 17 см.
Длину ломаной можно узнать двумя способами.
1) Узнать длину каждого звена ломаной и найти сумму этих длин можно так: 5 + 3 + 3 = 11 (см).
А можно так:
2) Начертить прямую. С помощью циркуля отложить на прямой один за другим отрезки, равные по длине звеньям ломаной, и узнать длину всего получившегося отрезка (11 см).
Сравни эти два способа: сколько измерений сделали в первом случае? во втором? Сделай вывод.
reshalka.com
ГДЗ учебник по математике 2 класс Моро. Часть 1. Страница 32. Номер №1
Решение
В первом случае с помощью линейки сделали 3 измерения:
1) измерили длину первого отрезка;
2) измерили длину второго отрезка;
3) измерили длину третьего отрезка.
Во втором случае сделали одно измерение:
измерили суммарную длину трех отрезков.
Вывод: в первом случае мы сделали больше измерений, но меньше действий, а во втором − наоборот, мы сделали много действий, но всего одно измерение. Но так как в первом случае не надо делать лишних чертежей, можно сказать, что этот способ проще.
Геометрическая фигура ломаная состоит из нескольких отрезков с общими начальными и конечными точками.
Отрезки называют звеньями ломаной, а точки — вершинами ломаной.
Если начальная и конечная точка ломаной совпадают, то такую ломаную называют замкнутой.
Если звенья ломаной пересекаются, то такую ломаную называют самопересекающейся.
При назывании ломаной соблюдается последовательность вершин. Если ломаная не замкнутая, то первой пишется название начальной вершины. Для замкнутых ломаных название можно начинать с любой вершины.
Пример:
описание рисунка.
-
У нарисованной не замкнутой ломаной (ABCDE) — (5) вершин и (4) звена;
-
У замкнутой ломаной (FHG) — (3) звена;
-
Одна из самопересекающихся ломаных — (KLMN) — не замкнутая, другая — (TPZV) — замкнутая.
Свойствa ломаной.
1. Длину ломаной определяют как сумму длин звеньев ломаной.
2. Длина отрезка, соединяющего начало и конец ломаной, меньше длины ломаной.
Лекция: Длина отрезка, ломаной, окружности, периметр многоугольника
Если на некоторой прямой имеются две точки, то прямая, ограниченная данными точками называется отрезком.
Для определения длины отрезка необходимо узнать расстояние от одной точки до другой.
Ломаная – это линия, состоящая из некоторого количества различных отрезков.
Для нахождения длины ломаной линии необходимо найти сумму длин всех отрезков.
Для нахождения длины предложенной ломаной следует сложить длины каждого её звена: AB +BC + CD + DE = 64 + 62 + 127 + 52 = 305 (см).
Важно понимать, что отрезки ломанной линии должны находится под углом, отличным от 180 градусов.
Ломаная линия может быть замкнутой или разомкнутой. Если ломаная линия замкнута, то она образует многоугольник.
В данном случае длина ломаной линии и будет являться периметром образованного многоугольника.
На рисунке изображен многоугольник, образованный ломанной ABCDEFА. Чтобы найти периметр многоугольника, следует найти длину заданной ломанной.
Окружность – это частный случай замкнутой кривой. Длина окружности – это длина кривой.
Если кривую, которая образует окружность, выровнять, то можно было бы найти расстояние полученного отрезка. Однако найти длину окружности можно проще. Для этого необходимо провести линию, которая будет проходить через центр, и узнать расстояние отрезка, ограниченного окружностью – это и будет диаметр данной окружности. Длина окружности находится по формуле: