Как найти сумму длин всех рёбер параллелепипеда
У вас возникло затруднение в решении геометрической задачи, связанной с параллелепипедом. Принципы решения таких задач, основанные на свойствах параллелепипеда, изложены в простой и доступной форме. Понять – значит решить. Подобные задачи больше не будут вызывать у вас затруднений.
Инструкция
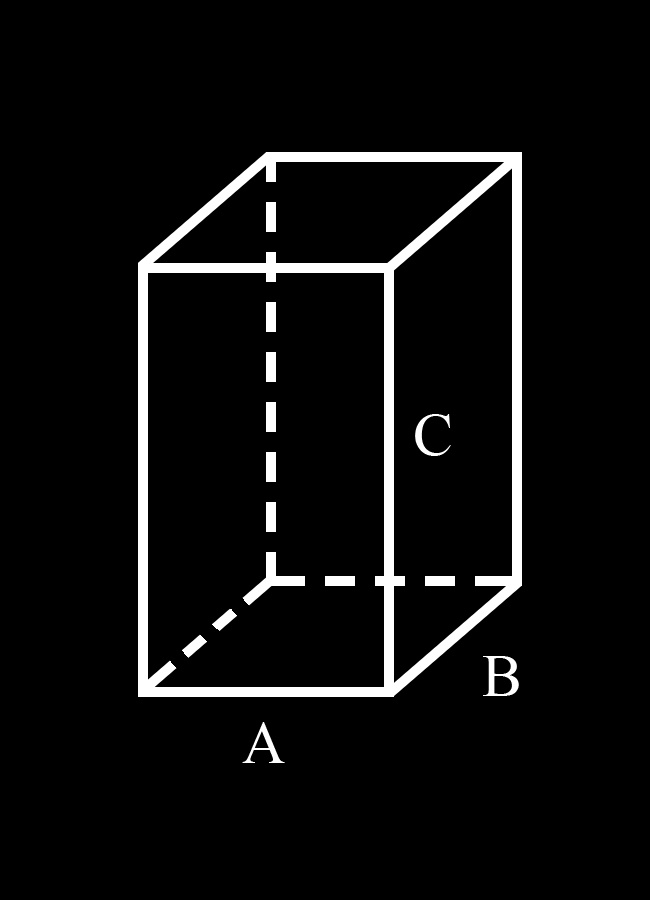
Для удобства введем обозначения:А и В стороны основания параллелепипеда; С – его боковая грань.
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Нужно просто хорошо усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.
Параллелепипед – это призма, основанием которой является параллелограмм.
Параллелепипед имеет 6 граней, и все они являются параллелограммами.
Противоположные грани равны и параллельны. Это важно.
Источники:
- сумма длин ребер прямоугольного параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Ольга Копотева
Знаток
(493)
7 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
Юрий Гринькин
Знаток
(327)
6 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Панкратова Татьяна
Знаток
(260)
4 года назад
как найти сумму длин всех ребер параллелепипеда
Кариночка Ученик (158), Вопрос решён 5 лет назад
11 Нравится Ответить
ЛУЧШИЙ ОТВЕТ
Анна Храпко 7 лет назад
Знаток (276)
L=4(a+b+c)
26 Нравится Пожаловаться
16 ОТВЕТОВ
ЛИЛИЯ Шевченко 3 года назад
Ученик (103)
L=4a+4b+4c
8 Нравится Пожаловаться
Ян Серебряков 3 года назад
Ученик (136)
L=4a+4b+4
2 Нравится Пожаловаться
Артём Фризен 3 года назад
Знаток (309)
L=4(a+b+c)
2 Нравится Пожаловаться
Ольга Копотева 2 года назад
Ученик (230)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
5 Нравится Пожаловаться
Юлия Моисеева 2 года назад
Ученик (133)
L=4(a+b+c)
2 Нравится Пожаловаться
katja maslova 2 года назад
Ученик (204)
L=4(a+b+c)
1 Нравится Пожаловаться
Eekler 2 года назад
Профи (633)
L=4(a+b+c)
Нравится Пожаловаться
Яна Подосенова 2 года назад
Ученик (166)
L=4(a+b+c)
Нравится Пожаловаться
Юрий Гринькин 2 года назад
Знаток (302)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение з
Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)
Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)
Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc
У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tanα=a/d_3 =a/√(b^2+c^2 )
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ – длина;
$b$ – ширина;
$с$ – высота(она же боковое ребро);
$P_{осн}$ – периметр основания;
$S_{осн}$ – площадь основания;
$S_{бок}$ – площадь боковой поверхности;
$S_{п.п}$ – площадь полной поверхности;
$V$ – объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ – длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ – высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ – это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ – радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ – радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ – катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ – длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции. - Квадрат.
$S=a^2$, где $а$ – сторона квадрата.
Пример:
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ – стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
- Учебники
- 5 класс
- Математика 👍
- Мерзляк
- №600

авторы: Мерзляк, Полонский, Якир.
издательство: Вентана-Граф, 2018 г.
Посмотреть глоссарий
Математика 5 класс Мерзляк. Номер №600
- Предыдущее
- Следующее
Найдите сумму длин всех ребер прямоугольного параллелепипеда, измерения которого равны 13 см, 16 см, 21 см.

reshalka.com
Математика 5 класс Мерзляк. Номер №600
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
![]() Посмотреть калькулятор Натуральные числа
Посмотреть калькулятор Натуральные числа
13 * 4 + 16 * 4 + 21 * 4 = 4 * (13 + 16 + 21) = 4 * 50 = 200 см сумма длин всех ребер прямоугольного параллелепипеда.
- Предыдущее
- Следующее
Нашли ошибку?
Посмотреть глоссарий
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
