-
- 0
-
?

-
Комментариев (0)
-
- 0
-
Помещаешь вектор а в конец вектора b, затем соединяешь начало вектора b и конец вектора a. Получившийся вектор будет суммой векторов a и b. Длину вектора находим по теореме Пифагора: = 5

-
Комментариев (0)
Ваш ответ
Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1.
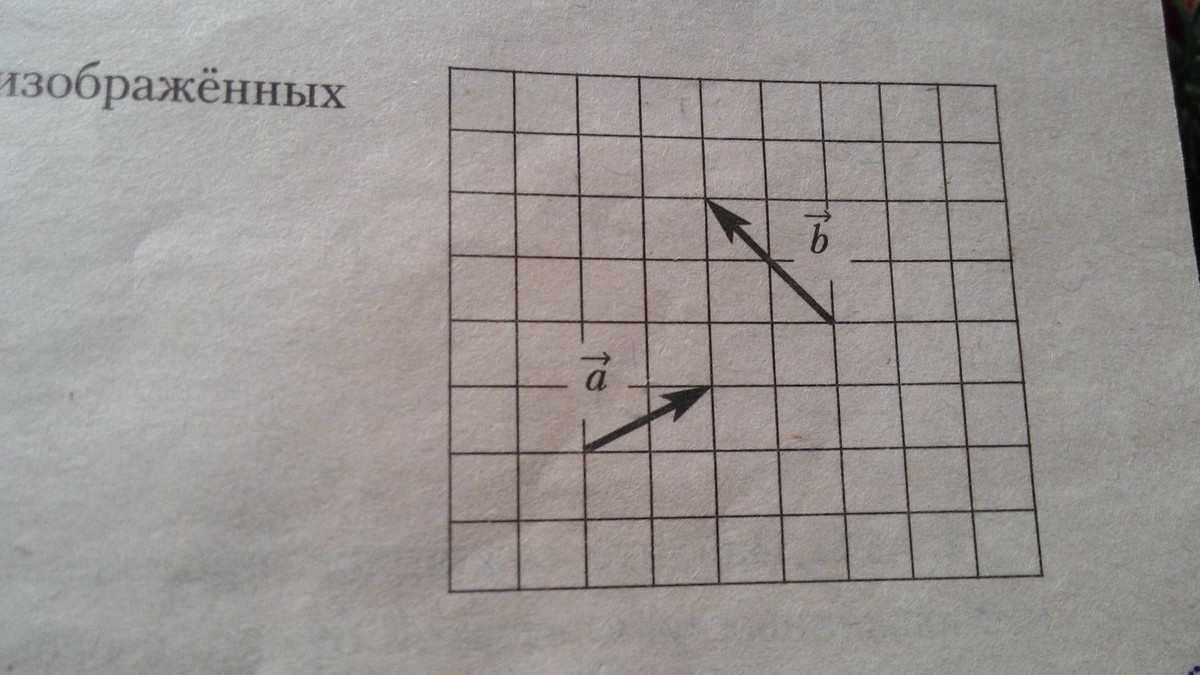
На этой странице вы найдете ответ на вопрос Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1?. Вопрос
соответствует категории Геометрия и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
xakeraverki23
Вопрос по геометрии:
Найдите длину суммы векторов a и b,изображенных на клетчатой бумаге с размером клетки 1 на 1.
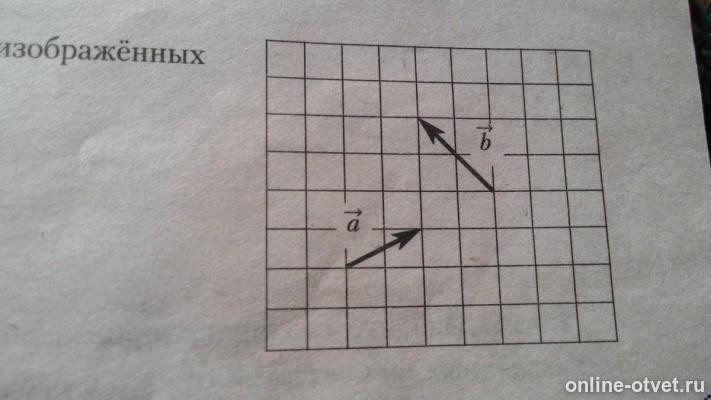
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
nsldreyed373
Рисуем вектора рядом, так, чтобы из конца вектора А начинался вектор B, при этом сохраняем их направление, теперь по клеточкам считаем расстояние от начала вектора А до конца вектора В.
Ответ: 3 клеточки.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Сумма векторов. Длина вектора. Задачи!
Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.
Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
Вектор — это направленный отрезок.
Все векторы, имеющие одинаковое направление и равные по длине являются равными.
*Все представленные выше четыре вектора равны!
То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.
Вектор может быть обозначен латинскими заглавными буквами, например:
При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.
Ещё вектор обозначается одной буквой латинского алфавита (прописной):
Возможно также обозначение без стрелок:
Суммой двух векторов АВ и ВС будет являться вектор АС .
Записывается как АВ + ВС = АС .
Это правило называется – правилом треугольника.
То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).
Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:
Перенесём вектор b, или по-другому – построим равный ему:
Как находится сумма нескольких векторов? По тому же принципу:
Это правило является следствием изложенного выше.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a, и мы можем построить вектор, который будет являться их суммой:
Ещё немного важной информации, необходимой для решения задач.
Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:
Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.
Пусть даны два вектора, найдём их разность:
Мы построили вектор противоположный вектору b, и нашли разность.
Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:
То есть, координаты вектора представляют собой пару чисел.
И координаты векторов имеют вид:
Модулем вектора называется его длина, определяется по формуле:
Формула для определения длины вектора, если известны координаты его начала и конца:
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО .
Найдём вектор, который будет являться результатом АО – ВО:
АО – ВО = АО +(– ВО )= АВ
То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ + AD .
Найдём вектор, который будет являться суммой векторов AD и AB . Вектор BC равен вектору AD . Значит AB + AD = AB + BC = AC
Длина вектора AC это длина диагонали ромба АС, она равна 16.
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО + ВО .
Найдём вектор, который будет являться суммой векторов АО и ВО . Вектор ВО равен вектору OD, з начит
Длина вектора AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:
По теореме Пифагора:
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО – ВО .
Найдём вектор, который будет являться результатом АО – ВО :
Длина вектора АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:
По теореме Пифагора:
Стороны правильного треугольника ABC равны 3.
Найдите длину вектора АВ – АС .
Найдём результат разности векторов:
Длина вектора СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.
27663. Найдите длину вектора а (6;8).
27664. Найдите квадрат длины вектора АВ .
27707. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АС .
27708. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов AB и AD .
27709. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов AB и AD .
27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов АО и ВО .
27713. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ .
27715. Диагонали ромба ABCD равны 12 и 16.
Найдите длину вектора АВ – AD .
27716. Диагонали ромба ABCD равны 12 и 16.
Найдите длину вектора АВ – АС .
Стороны правильного треугольника ABC равны 2√3. Найдите длину вектора АВ + АС .
В будущем мы продолжим рассматривать задачи с векторами, не пропустите! Задания будут связаны с координатами векторов, скалярным произведением.
На этом всё. Успеха вам!
С уважением, Александр
Вступительный экзамен по математике. Преподаватели приглашают первого абитуриента:
— Сколько будет два плюс два?
— Три! — Нет! — Пять! — Нет! — Шесть!
— Неправильно! Да… дурак, но ищущий… берем!
Заходит второй абитуриент:
— Сколько будет два плюс два?
— Три! — Нет! — Три! — Нет! — Три!
— Неправильно! Да… дурак, но настырный… берем!
Заходит третий абитуриент:
— Сколько будет два плюс два?
— Четыре, конечно!
— Да… умный. Но мест уже нет!
Сложение векторов: длина суммы векторов и теорема косинусов
Определения скалярного произведения векторов через угол между ними
Сложение векторов по правилу треугольника (суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора приложено к концу вектора ) даёт возможность упрощать выражение перед вычислением произведений векторов.
Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке “Векторы и операции над векторами”.
Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С – не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия – одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.
При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть и – векторы, – угол между ними, а – сумма векторов как результат сложения векторов по правилу треугольника. Тогда верно следующее соотношение:
,
где – угол, смежный с углом . У смежных углов одна сторона общая, а другие стороны лежат на одной прямой (см. рисунок выше).
Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:
.
В случае вычитания векторов () происходит сложение вектора с вектором , противоположным вектору , то есть имеющим ту же длину, но противоположным по направлению. Углы между и и и между и являются смежными углами, у них, как уже было отмечено, одна сторона общая, а другие стороны лежат на одной прямой. В случае вычитания векторов для нахождения длины разности векторов нужно знать следующее свойство косинусов смежных углов:
косинусы смежных углов равны по абсолютной величине (величине по модулю), но имеют противоположные знаки.
Перейдём к примерам.
Сложение векторов – решение примеров
Пример 1. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .
Решение. Из элементарной тригонометрии известно, что .
Шаг 1. Выполняем сложение векторов. Находим длину суммы векторов, поставляя в формулу длины косинус угла, смежного с углом между векторами:
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус “изначального” угла:
Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Пример 2. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .
Пример 3. Даны длины векторов и длина их суммы . Найти длину их разности .
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:
Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус “изначального” угла будет со знаком плюс.
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус “изначального” угла:
Пример 4. Даны длины векторов и длина их разности . Найти длину их суммы .
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус “изначального” угла (задача обратная по отношению к примеру 1) и находим его:
Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между и :
Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:
Пример 5. Векторы и взаимно перпендикулярны, а их длины . Найти длину их суммы и и длину их разности .
Два смежных угла, как нетрудно догадаться из приведённого в начале урока определения, в сумме составляют 180 градусов. Следовательно, смежный с прямым углом (90 градусов) угол – тоже прямой (тоже 90 градусов). Косинус такого угла равен нулю, то же самое относится и к косинусу смежного угла. Поэтому, подставляя это значение в выражения под корнем в формуле длины суммы и разности векторов, получаем нули как последние выражения – произведения под знаком корня. То есть длины суммы и разности данных векторов равны, вычисляем их:
Пример 6. Какому условию должны удовлетворять векторы и , чтобы имели место слелующие соотношения:
1) длина суммы векторов равна длине разности векторов, т. е. ,
2) длина суммы векторов больше длины разности векторов, т. е. ,
3) длина суммы векторов меньше длины разности векторов, т. е. ?
Находим условие для первого соотношения. Для этого решаем следующее уравнение:
То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.
Находим условие для второго соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).
Находим условие для третьего соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.
Сложение и вычитание векторов.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Сложение и вычитание векторов.
Сумма двух векторов. Законы сложения векторов. Правило параллелограмма.
Представим себе такую ситуацию. Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой. Сейчас мы описали принцип первого правила сложения векторов.
Чтобы найти вектор суммы двух векторов и , нужно:
совместить параллельным переносом начало вектора с концом вектора ;
провести вектор из начала вектора в конец вектора ;
получившийся вектор и есть вектор суммы: .
Если к вектору прибавить нулевой вектор по правилу треугольника, то получим вектор , т.е. справедливо равенство: .
Утверждение. Если и – произвольные точки, то .
Сложение векторов подчиняется алгебраическим законам.
ТЕОРЕМА. Для любых векторов и справедливы равенства:
Доказательство теоремы в случае, когда векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно. Мы рассмотрим случай, когда данные векторы неколлинеарны.
1). Отметим произвольную точку и отложим от этой точки вектор . Воспользуемся правилом треугольника и прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок слева).
Теперь от точки и отложим вектор . По правилу треугольника прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок справа).
– параллелограмм и точка совпадает с точкой . Значит, , т.е.
2). От точки отложим вектор , от точки отложим вектор , а от точки – вектор . Найдём суммы векторов по правилу треугольника.
При доказательстве первой формулы получился параллелограмм, причём, из точки выходят два вектора и , а вектор их суммы является диагональю параллелограмма. На основе этого возникает второе правило геометрического сложения векторов.
Чтобы найти вектор суммы двух векторов и , нужно:
совместить параллельным переносом начала векторов и ;
на этих векторах достроить параллелограмм;
вектором суммы является вектор, который лежит на диагонали параллелограмма, имеющий своё начало в начале исходных векторов.
Сумма нескольких векторов.
Сложение нескольких векторов происходит по принципу правила треугольника. Складываются два вектора, к вектору суммы прибавляется следующий вектор и т.д. Приведём пример.
Отметим точку и отложим от неё вектор . Прибавим к нему вектор по правилу треугольника. . Теперь к вектору прибавим вектор . . К вектору прибавляем вектор . . Осталось к вектору прибавить вектор . .
Итак, . Значит, суммой векторов является вектор, с началом в начале первого вектора и концом – в конце последнего. Такое сложение векторов называется правилом многоугольника.
Чтобы найти вектор суммы нескольких векторов, нужно:
последовательно совместить параллельным переносом начало последующего вектора с концом предыдущего;
вектором суммы всех векторов является вектор, с началом в начале первого вектора и концом – в конце последнего.
Определение. Разностью двух векторов и называется такой вектор , что при сложении его с вектором получается вектор .
Вычитание векторов можно производить, руководствуясь двумя понятиями: следствием из правила треугольника сложения векторов; определением разности двух чисел. Разберём каждое из них.
Сложим векторы и по правилу треугольника. По рисунку видно, что . Отсюда, и . Значит, разность двух векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда два правила:
Чтобы найти вектор разности двух векторов, нужно:
совместить параллельным переносом начала этих векторов;
вектором разности является вектор с началом в конце второго вектора и концом в конце первого вектора.
Чтобы найти вектор разности двух векторов, нужно:
совместить параллельным переносом концы этих векторов;
вектором разности является вектор с началом в начале первого вектора и концом в начале второго вектора.
Далее, из алгебры мы знаем, что для того, чтобы из числа вычесть число , нужно к числу прибавить число, противоположное числу , т.е. . Такое же правило справедливо и для векторов.
ТЕОРЕМА. Для любых векторов справедливо равенство:
1. Найдём разность векторов по I правилу. Вектором разности является вектор (рисунок слева). А теперь найдём сумму векторов по правилу треугольника, где – вектор, противоположный вектору . Вектором суммы является вектор (рисунок справа). Не трудно заметить, что . Они сонаправлены и имеют одинаковые модули.
2. А теперь докажем то же самое аналитически. По определению разности векторов,
Что и требовалось доказать.
Из этой теоремы следует третье правило вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный второму.
Используя это правило вычитания векторов, способ сложения векторов выбирается произвольно.
Вектор является суммой векторов и . Определите, какой из четырёх рисунков верный.
Проведите векторы . Какая геометрическая фигура у вас получилась?
Вектор является разностью векторов и . Определите, какой из четырёх рисунков верный.
Вектор является суммой векторов и . Определите, какой из четырёх рисунков верный.
Выразите вектор через векторы , используя рисунок.
Выразите вектор через векторы , используя рисунок.
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?
В квадрате проведены диагонали и . Укажите номера верных утверждений.
– параллелограмм. Найдите сумму векторов .
– прямоугольник. Диагонали и пересекаются в точке . Укажите номера верных утверждений.
параллелограмм. Выразите векторы и через векторы и .
– параллелограмм. Выразите векторы и через векторы и .
– прямоугольник. Выразите векторы и через векторы и .
– параллелограмм. Выразите векторы и через векторы и .
Найдите длины векторов , изображённых на клетчатой бумаге с размерами клетки 1 х 1.
Две стороны прямоугольника равны 20 и 21. Найдите длину суммы векторов и .
Две стороны прямоугольника равны 7 и 24. Найдите длину разности векторов и .
На каждом рисунке найдите длину вектора (размеры клетки 1 х 1).
На каждом рисунке найдите длину суммы векторов и (размеры клетки 1 х 1).
На каждом рисунке найдите длину разности векторов и , изображённых на клетчатой бумаге с размерами клетки 1 х 1.
Краткое описание документа:
Теоретическая часть данной разработки содержит определения, свойства, правила, связанные с геометрическим сложением и вычитанием векторов. К каждому понятию предложен рисунок, разобраны примеры. Практическая часть разработки содержит задания на построение суммы и разности векторов, а также аналитическое определение суммы и разности векторов. Есть задания, встречающиеся на ОГЭ.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 943 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 679 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 306 человек из 67 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 503 229 материалов в базе
Материал подходит для УМК
«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
§ 2. Сложение и вычитание векторов
Другие материалы
- 16.10.2019
- 800
- 0
- 16.10.2019
- 205
- 0
- 15.10.2019
- 133
- 0
- 15.10.2019
- 151
- 1
- 15.10.2019
- 145
- 2
- 15.10.2019
- 913
- 0
- 20.09.2019
- 211
- 0
- 19.09.2019
- 1224
- 247
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 16.10.2019 4023
- DOCX 370.1 кбайт
- 72 скачивания
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Колесник Марина Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 года и 10 месяцев
- Подписчики: 0
- Всего просмотров: 260707
- Всего материалов: 132
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Большинство российских вузов используют смешанный формат обучения
Время чтения: 1 минута
В Петербурге введут новые COVID-ограничения для несовершеннолетних
Время чтения: 2 минуты
В Москве отмечается беспрецедентный рост заболеваемости коронавирусом среди детей
Время чтения: 2 минуты
Каждый второй российский студент недоволен своим вузом
Время чтения: 1 минута
Большинство российских школьников недовольны качеством питания в столовых
Время чтения: 1 минута
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
[spoiler title=”источники:”]
http://function-x.ru/vectors_cosinus.html
http://infourok.ru/slozhenie-i-vichitanie-vektorov-3887260.html
[/spoiler]
