Ольга Копотева
Знаток
(493)
7 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
Юрий Гринькин
Знаток
(327)
6 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Панкратова Татьяна
Знаток
(260)
4 года назад
как найти сумму длин всех ребер параллелепипеда
Кариночка Ученик (158), Вопрос решён 5 лет назад
11 Нравится Ответить
ЛУЧШИЙ ОТВЕТ
Анна Храпко 7 лет назад
Знаток (276)
L=4(a+b+c)
26 Нравится Пожаловаться
16 ОТВЕТОВ
ЛИЛИЯ Шевченко 3 года назад
Ученик (103)
L=4a+4b+4c
8 Нравится Пожаловаться
Ян Серебряков 3 года назад
Ученик (136)
L=4a+4b+4
2 Нравится Пожаловаться
Артём Фризен 3 года назад
Знаток (309)
L=4(a+b+c)
2 Нравится Пожаловаться
Ольга Копотева 2 года назад
Ученик (230)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
5 Нравится Пожаловаться
Юлия Моисеева 2 года назад
Ученик (133)
L=4(a+b+c)
2 Нравится Пожаловаться
katja maslova 2 года назад
Ученик (204)
L=4(a+b+c)
1 Нравится Пожаловаться
Eekler 2 года назад
Профи (633)
L=4(a+b+c)
Нравится Пожаловаться
Яна Подосенова 2 года назад
Ученик (166)
L=4(a+b+c)
Нравится Пожаловаться
Юрий Гринькин 2 года назад
Знаток (302)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение з
Формула суммы длин всех рёбер параллелепипеда. Как найти сумму длин всех рёбер параллелепипеда
«Вычисление объёма параллелепипеда» – 2. Объем прямоугольного параллелепипеда. Задание 1: Вычислить объемы фигур. 1. Математика 5 класс. 3. 4.
«Прямоугольный параллелепипед 5 класс» – Что такое объем? Прямоугольный параллелепипед. Другая формула объема прямоугольного параллелепипеда. Объем прямоугольного параллелепипеда. Формула объема куба. Пример. Объем куба. Вершин – 8. Математика, 5 класс Логунова Л.В. Ребер – 12. Куб. Кубический сантиметр. Ребро куба равно 5 см. Граней – 6.
«Урок Прямоугольный параллелепипед» – 12. С1. В1. Длина. Параллелепипед. Вершины. Ребра. А1. Ширина. D. Грани. D1. 8. В. Прямоугольный параллелепипед.
«Объем параллелепипеда» – Значит, по правилу вычисления объема, получаем: 3х3х3=27 (см3). Еще в древности людям требовалось измерять количества каких-либо веществ. В литрах обычно измеряют объемы жидкостей и сыпучих веществ. В Древнем Вавилоне единицами объемов служили кубы. Теперь определим что же такое единицы объемов? Тема урока: Объем параллелепипеда.
«Прямоугольный параллелепипед» – Параллелепипед. Прямоугольный параллелепипед. МОУ «Гимназия» №6. Слово встречалось у древнегреческих ученых Евклида и Герона. Работу выполнила Ученица 5 «В» класса Мендыгалиева Алина. Длина Ширина Высота. Параллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Вершины. Грани параллелепипеда, не имеющие общих вершин, называются противоположными.
«Объем прямоугольного параллелепипеда» – Ребрами. 3. БЛИЦ – ОПРОС (I часть). A, в, с, d. Объемная. Какие ребра равны ребру АЕ? AE, EF, EH. 1. Любой куб является прямоугольным параллелепипедом. Квадраты. 5. У куба все ребра равны. 8. Прямоугольник. 12. 3. У куба все грани являются квадратами. Назовите ребра, имеющие вершину E.
Всего в теме
35 презентаций
В геометрических задачах довольно часто возникает необходимость нахождения каких-либо характеристик прямоугольного параллелепипеда. На самом деле, это задача несложная.
Для того, чтобы её решить, необходимо знать свойства параллелепипеда. Если их понять, то и решать задачи потом будет не так сложно. В качестве примера попробуем найти сумму длин всех рёбер прямоугольного параллелепипеда.
Быстрая навигация по статье
Подготовка
Для того чтобы было удобно, необходимо определиться с обозначениями: стороны прямоугольного параллелепипеда назовём А и В, а его боковую грань – С.
Теперь, если внимательно присмотреться, можно сделать вывод, что в основании прямоугольного параллелепипеда лежит параллелограмм. Все его рёбра, при этом, будут иметь длины сторон А и В.
Найти сумму длин всех рёбер можно будет только в том случае, если понимать, что такое параллелограмм. Для тех, кто не помнит, следует сказать, что параллелограмм – это четырёхугольник, противоположные стороны которого равны между собой и параллельны.
Рассуждения
У параллелограмма противоположные стороны равны между собой. Получается, что напротив стороны А лежит такая же сторона А. Исходя из определения параллелограмма понятно, что верхняя грань его тоже равна А. Получается, что сумма длин всех сторон данного параллелограмма равна 4А.
Аналогичные рассуждения могут быть приведены и для стороны В — получается, что сумма сторон параллелограмма, созданного из стороны В, будет равняться 4 В.
Если внимательно присмотреться, то можно сделать вывод, что боковые грани прямоугольного параллелепипеда – это тоже параллелограммы. Причём, ребро С одновременно относится к двум соседним граням прямоугольного параллелепипеда. И аналогично представленными выше рассуждениям, сумма длин всех рёбер будет равняться 4 С.
Решение
Теперь остаётся найти сумму длин всех рёбер просто просуммировав все прямоугольные параллелограммы. И получается, что эта сумма равняется: 4А+4В+4С или 4(А+В+С).
Можно рассмотреть частный случай, когда необходимо будет найти сумму длин всех рёбер не прямоугольного параллелепипеда, а куба — в таком случае эта сумма будет равна 12 А.
Для того чтобы решить любые геометрические задачи, всегда надо хорошо знать определения, в чём вы только что и убедились.
У вас появилось затруднение в решении геометрической задачи, связанной с параллелепипедом. Тезисы решения таких задач, основанные на свойствах параллелепипеда
, высказаны в примитивный и доступной форме. Осознать – значит решить. Сходственные задачи огромнее не будут вызывать у вас сложностей.
Инструкция
1.
Для комфорта введем обозначения:А и В стороны основания параллелепипеда
; С – его боковая грань.
2.
Таким образом, в основании параллелепипеда
лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что супротив стороны А лежит равная ей сторона А. От того что противолежащие грани параллелепипеда
равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3.
То же дозволено сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда
равна В. Верхняя (противолежащая) грань параллелепипеда
тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4.
Боковые грани параллелепипеда
тоже являются параллелограммами (вытекает из свойств параллелепипеда
). Ребро С единовременно является стороной 2-х соседних граней параллелепипеда
. От того что противоположные грани параллелепипеда
попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5.
Таким образом, сумма всех ребер параллелепипеда
: 4А+4В+4С либо 4(А+В+С)Частный случай прямого параллелепипеда
– куб. Сумма всех его ребер равна 12А.Таким образом, решение задачи касательно пространственного тела неизменно дозволено свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Надобно примитивно отменно усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.Параллелепипед – это призма, основанием которой является параллелограмм. Параллелепипед имеет 6 граней, и все они являются параллелограммами. Противоположные грани равны и параллельны. Это главно.
1) Параллелепипед – это называется призма, основание которой параллелограм. Все грани параллелепипеда – параллелограммы. Параллелепипед, четыре боковые грани которого – прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
2) У прямоугольного параллелепипеда 12 ребер. Причем, среди них есть равные и их по 4.
3) Таким образом, (13 + 16 + 21) * 4 = 50 * 4 = 200 см – сумма длин всех ребер параллелепипеда.
Ответ: 200 см.
Понятие прямоугольного параллелепипеда
Прямоугольный параллелепипед представляет собой многогранник, построенный из шести граней, каждая из которых прямоугольник. Противолежащие грани параллелепипеда равны. У прямоугольного параллелепипеда 12 ребер и 8 вершин. Три ребра, выходящие из одной вершины, называют измерениями параллелепипеда или его длиной, высотой и шириной. Таким образом, у прямоугольного параллелепипеда есть четверки равных по длине ребер: 4 высоты, 4 ширины и 4 длины.
Форму прямоугольного параллелепипеда имеют, например:
- кирпич;
- домино;
- коробок спичек;
- аквариум;
- пачка сигарет;
- дипломат;
- ящик.
Частным случаем прямоугольного параллелепипеда является куб. Куб – это геометрическое тело в форме прямоугольного параллелепипеда, но при этом все его грани имеют форму квадрата, поэтому все его ребра равны. У куба 6 граней (равных друг другу по площади), 12 ребер (равных друг другу по длине) и 8 вершин.
Вычисление суммы длин всех ребер прямоугольного параллелепипеда
Обозначим измерения параллелепипеда: a – длина, b – ширина, c – высота.
Дано: a = 13 см, b = 16 см, c = 21 см.
Найти: сумму длин всех ребер прямоугольного параллелепипеда.
Так как прямоугольный параллелепипед имеет 4 высоты, 4 ширины и 4 длины (равных между собой), то:
1) 4 * 13 = 52 (см) – сумма длин параллелепипеда;
2) 4 * 16 = 64 (см) – суммарное значение ширины параллелепипеда;
3) 4 * 21 = 84 (см) – сумма высот параллелепипеда;
4) 52 + 64 + 84 = 200 (см) – сумма длин всех ребер прямоугольного параллелепипеда.
Таким образом, для нахождения суммы длин всех ребер прямоугольного параллелепипеда можно вывести формулу: Z = 4a + 4b + 4c (где Z – сумма длин ребер).
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория “Ахиллес и черепаха”. Вот как она звучит:
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что “… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса…
” [Википедия, ” Апории Зенона “]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие “бесконечность” в этой ситуации, то правильно будет говорить “Ахиллес бесконечно быстро догонит черепаху”.
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию “Ахиллес и черепаха” очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто – достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве – это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
среда, 4 июля 2018 г.
Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.
Как видите, “во множестве не может быть двух идентичных элементов”, но если идентичные элементы во множестве есть, такое множество называется “мультимножество”. Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова “совсем”. Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики не прятались за фразой “чур, я в домике”, точнее “математика изучает абстрактные понятия”, есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его “математическое множество зарплаты”. Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
В первую очередь, сработает логика депутатов: “к другим это применять можно, ко мне – низьзя!”. Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами – на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует – всё решают шаманы, наука здесь и близко не валялась.
Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова – значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов – у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких “мыслимое как не единое целое” или “не мыслимое как единое целое”.
воскресенье, 18 марта 2018 г.
Сумма цифр числа – это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.
Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу “Сумма цифр числа”. Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры – это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: “Найти сумму графических символов, изображающих любое число”. Математики эту задачу решить не могут, а вот шаманы – элементарно.
Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.
1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.
2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки – это не математическое действие.
3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.
4. Складываем полученные числа. Вот это уже математика.
Сумма цифр числа 12345 равна 15. Вот такие вот “курсы кройки и шитья” от шаманов применяют математики. Но это ещё не всё.
С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.
Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых – нет. Реальность состоит не только из чисел.
Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.
Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.
Табличка на двери
Открывает дверь и говорит:
Ой! А это разве не женский туалет?
– Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?
Женский… Нимб сверху и стрелочка вниз – это мужской.
Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,
Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:
Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
1А – это не “минус четыре градуса” или “один а”. Это “какающий человек” или число “двадцать шесть” в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.
Как найти сумму длин всех рёбер параллелепипеда
У вас возникло затруднение в решении геометрической задачи, связанной с параллелепипедом. Принципы решения таких задач, основанные на свойствах параллелепипеда, изложены в простой и доступной форме. Понять – значит решить. Подобные задачи больше не будут вызывать у вас затруднений.
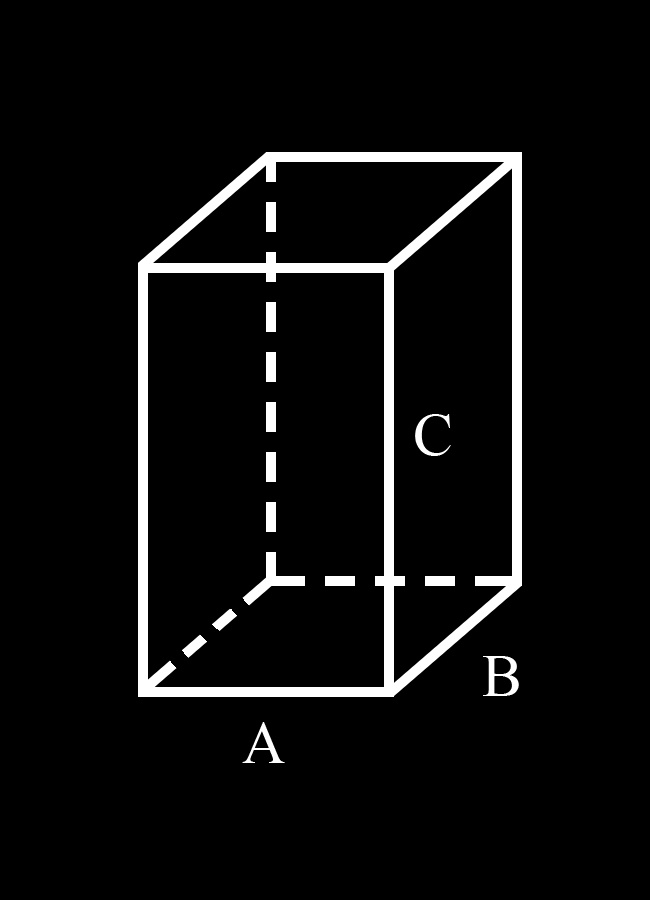
Инструкция
Для удобства введем обозначения:А и В стороны основания параллелепипеда; С – его боковая грань.
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Нужно просто хорошо усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.
Параллелепипед – это призма, основанием которой является параллелограмм.
Параллелепипед имеет 6 граней, и все они являются параллелограммами.
Противоположные грани равны и параллельны. Это важно.
Источники:
- сумма длин ребер прямоугольного параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
По условию задачи дан прямоугольный параллелепипед ABCDA1B1C1D1 с измерениями a; b и c:
a = 0,24 м;
b = 0,4 м;
с = 1,5 м;
В задаче требуется найти объем, площадь поверхности и сумму длин всех ребер этого параллелепипеда.
Формула для площади поверхности
У параллелепипеда шесть граней:
- нижнее основание ABCD;
- верхнее основание A1B1C1D1;
- четыре боковые грани AA1B1B; BB1C1C; CC1D1D; DD1A1A.
В прямоугольном параллелепипеде все грани являются прямоугольниками, а ребра равны:
|AB| = |CD| = |A1B1| = |C1D1| = а;
|BC| = |AD| = |B1C1| = |A1D1| = b;
|AA1| = |BB1| = |CC1| = |DD1| = c.
Сумма L длин всех 12 ребер равна:
L = 4 * a + 4 * b + 4 * c = 4 * (a + b + c);
Площадью поверхности параллелепипеда называют сумму площадей всех шести граней. Площади оснований одинаковы:
S1 = |AB| * |BC| = |A1B1| * |B1C1| = a * b;
Площади боковых граней AA1B1B и CC1D1D одинаковы и равны:
S2 = |AB| * |AA1| = |CD| * |CC1| = a * c;
Равны и площади оставшихся двух граней BB1C1C и DD1A1A:
S3 = |BC| * |BB1| = |AD| * |AA1| = b * c;
Площадь поверхности равна:
S = 2 * S1 + 2 * S2 + 2 * S3 = 2 * a * b + 2 * a * c + 2 * b * c = 2 * (a * b + a * c + b * c);
Объем прямоугольного параллелепипеда равен проведению трех его измерений:
V = S1 * |AA1| = a * b * c;
Вычисление требуемых параметров
Подставляя исходные данные, получаем:
L = 4 * (0,24 + 0,4 + 1,5) = 8,56 (м);
S = 2 * (0,24 * 0,4 + 0,24 * 1,5 + 0,4 * 1,5) = 2,112 (м^2);
V = 0,24 * 0,4 * 1,5 = 0,144 (м^3);
Ответ: L = 8,56 (м); S = 2,112 (м^2); V = 0,144 (м^3);
