Решение уравнений с дробями

О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 – 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 – 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x – 2 – 7 x + 2 = 8 x 2 – 4
Начать следует с области допустимых значений:
x 2 – 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 – 4 = ( x – 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x – 2 – 7 x + 2 = 8 x 2 – 4
x ( x – 2 ) ( x + 2 ) x – 2 – 7 ( x – 2 ) ( x + 2 ) x + 2 = 8 ( x – 2 ) ( x + 2 ) ( x – 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) – 7 ( x – 2 ) = 8
x 2 + 2 x – 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 – 7 – x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 – 7 – x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ – 2
x 2 + 7 x + 10 ≠ 0
D = 49 – 4 · 10 = 9
x 1 ≠ – 7 + 3 2 = – 2
x 2 ≠ – 7 – 3 2 = – 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x – x 1 ) ( x – x 2 )
x x + 2 + x + 1 x + 5 – 7 – x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 – 7 – x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 –
– ( 7 – x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) – 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 – 7 + x = 0
2 x 2 + 9 x – 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x – 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x – 2 – 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x – 2 – 3 ( x – 2 ) x + 4 – 1 ( x – 2 ) ( x + 4 ) = 0
4 ( x + 4 ) – 3 ( x – 2 ) – ( x – 2 ) ( x + 4 ) ( x – 2 ) ( x + 4 ) = 0
4 x + 16 – 3 x + 6 – ( x 2 + 4 x – 2 x – 8 ) ( x – 2 ) ( x + 4 ) = 0
x + 22 – x 2 – 4 x + 2 x + 8 ( x – 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
– x 2 – x + 30 ( x – 2 ) ( x + 4 ) = 0 ⇔ – x 2 – x + 30 = 0 ( x – 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x – 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
– x 2 – x + 30 = 0 _ _ _ · ( – 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 – 2 x – x x – 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x – 2 ) – x x x – 2 – 3 ( x – 2 ) x = 0
x + 2 – x 2 – 3 ( x – 2 ) x ( x – 2 ) = 0
x + 2 – x 2 – 3 x + 6 x ( x – 2 ) = 0
– x 2 – 2 x + 8 x ( x – 2 ) = 0 ⇔ – x 2 – 2 x + 8 = 0 x ( x – 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
– x 2 – 2 x + 8 = 0 _ _ _ · ( – 1 )
Корни квадратного уравнения:
x 1 = – 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 – x – 6 x – 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 – x – 6 1 x – 3 – x ( x – 3 ) – 2 ( x – 3 ) = 0
x 2 – x – 6 – x ( x – 3 ) – 2 ( x – 3 ) x – 3 = 0
x 2 – x – 6 – x 2 + 3 x – 2 x + 6 x – 3 = 0
0 x x – 3 = 0 ⇔ 0 x = 0 x – 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x – 2 – 3 x + 2 = 20 x 2 – 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x – 2 – 3 ( x – 2 ) x + 2 – 20 1 ( x – 2 ) ( x + 2 ) = 0
5 ( x + 2 ) – 3 ( x – 2 ) – 20 ( x – 2 ) ( x + 2 ) = 0
5 x + 10 – 3 x + 6 – 20 ( x – 2 ) ( x + 2 ) = 0
2 x – 4 ( x – 2 ) ( x + 2 ) = 0 ⇔ 2 x – 4 = 0 ( x – 2 ) ( x + 2 ) ≠ 0
( x – 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x – 3 x – 5 + 1 x = x + 5 x ( x – 5 )
Начнем с определения ОДЗ:
– 5 ≠ 0 x ≠ 0 x ( x – 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x – 3 x – 5 + 1 x = x + 5 x ( x – 5 ) · x ( x – 5 )
( x – 3 ) x ( x – 5 ) x – 5 + x ( x – 5 ) x = ( x + 5 ) x ( x – 5 ) x ( x – 5 )
( x – 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 – 3 x + x – 5 = x + 5 → x 2 – 2 x – 5 – x – 5 = 0 → x 2 – 3 x – 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = – 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
Урок по теме “Решение дробных рациональных уравнений”. 8-й класс
Разделы: Математика
Класс: 8
Цели урока:
- формирование понятия дробных рационального уравнения;
- рассмотреть различные способы решения дробных рациональных уравнений;
- рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
- обучить решению дробных рациональных уравнений по алгоритму;
- проверка уровня усвоения темы путем проведения тестовой работы.
- развитие умения правильно оперировать полученными знаниями, логически мыслить;
- развитие интеллектуальных умений и мыслительных операций – анализ, синтез, сравнение и обобщение;
- развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
- развитие критического мышления;
- развитие навыков исследовательской работы.
- воспитание познавательного интереса к предмету;
- воспитание самостоятельности при решении учебных задач;
- воспитание воли и упорства для достижения конечных результатов.
Тип урока: урок – объяснение нового материала.
Ход урока
1. Организационный момент.
Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить? Какие нет и почему?

Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».
2. Актуализация знаний. Фронтальный опрос, устная работа с классом.
А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:
- Что такое уравнение? (Равенство с переменной или переменными.)
- Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа – в правую. Привести подобные слагаемые. Найти неизвестный множитель).
- Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
- Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
- Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
- Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)
3. Объяснение нового материала.
Решить в тетрадях и на доске уравнение №2.

Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).

х 2 -4х-2х+8 = х 2 +3х+2х+6
х 2 -6х-х 2 -5х = 6-8

Решить в тетрадях и на доске уравнение №4.

Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).

Теперь попытайтесь решить уравнение №7 одним из способов.
[spoiler title=”источники:”]
http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya
http://urok.1sept.ru/articles/559882
[/spoiler]
Решение уравнений с дробями

О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:


Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:


На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение: 
- Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Как решать уравнения с дробями. Показательное решение уравнений с дробями.
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
x=45-20=25
Другой пример, когда неизвестное находится в знаменателе:
Уравнения такого типа называются дробно-рациональными или просто дробными.
Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:
- значение переменной, обращающее в 0 знаменатель, корнем быть не может;
- нельзя делить или умножать уравнение на выражение =0.
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
Избавляемся от знаменателя путем умножения всех членов уравнения на х
И решаем обычное уравнение
5x – 2х = 1
3x = 1
х = 1/3
Решим уравнение посложнее:
Здесь также присутствует ОДЗ: х -2.
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):
Это самое обычное умножение дробей, которое мы уже рассмотрели выше
Запишем это же уравнение, но несколько по-другому
Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
х = 4 – 2 = 2, что соответствует нашей ОДЗ
Для закрепления материала рекомендуем еще посмотреть видео.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Алгебра. Урок 4. Уравнения, системы уравнений
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Линейные уравнения
Линейные уравнения
Линейное уравнение – уравнение вида a x = b , где x – переменная, a и b некоторые числа, причем a ≠ 0 .
Примеры линейных уравнений:
- 3 x = 2
- 2 7 x = − 5
Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.
Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.
Для того, чтобы решить линейное уравнение , необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного линейного уравнения: x = b a .
Примеры решения линейных уравнений:
- 2 x + 1 = 2 ( x − 3 ) + 8
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b :
Для начала раскроем скобки:
2 x + 1 = 4 x − 6 + 8
В левую часть переносятся все слагаемые с x , в правую – числа:
Теперь поделим левую и правую часть на число ( -2 ) :
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
x 2 + 3 x − 8 = x − 1
Это уравнение не является линейным уравнением.
Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)
- 2 x − 4 = 2 ( x − 2 )
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 2 x = − 4 + 4
И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 4 = 2 x − 16
2 x − 2 x = − 16 + 4
В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.
Квадратные уравнения
Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .
Алгоритм решения квадратного уравнения:
- Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
- Выписать, чему равны в числах коэффициенты: a = … b = … c = …
- Вычислить дискриминант по формуле: D = b 2 − 4 a c
- Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
- Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
- Если D 0, решений нет: x ∈ ∅
Примеры решения квадратного уравнения:
- − x 2 + 6 x + 7 = 0
a = − 1, b = 6, c = 7
D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64
D > 0 – будет два различных корня:
x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7
Ответ: x 1 = − 1, x 2 = 7
a = − 1, b = 4, c = − 4
D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0
D = 0 – будет один корень:
x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2
a = 2, b = − 7, c = 10
D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31
D 0 – решений нет.
Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!
Разложение квадратного трехчлена на множители
Квадратный трехчлен можно разложить на множители следующим образом:
a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )
где a – число, коэффициент перед старшим коэффициентом,
x – переменная (то есть буква),
x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.
Если квадратное уравнение имеет только один корень , то разложение выглядит так:
a x 2 + b x + c = a ⋅ ( x − x 0 ) 2
Примеры разложения квадратного трехчлена на множители:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2
Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:
- c = 0 ⇒ a x 2 + b x = x ( a x + b )
- b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.
Дробно рациональные уравнения
Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .
Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .
Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.
ОДЗ – область допустимых значений переменной.
В выражении вида f ( x ) g ( x ) = 0
ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).
Алгоритм решения дробно рационального уравнения:
- Привести выражение к виду f ( x ) g ( x ) = 0 .
- Выписать ОДЗ: g ( x ) ≠ 0.
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Пример решения дробного рационального уравнения:
Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.
Решение:
Будем действовать в соответствии с алгоритмом.
- Привести выражение к виду f ( x ) g ( x ) = 0 .
Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:
x 2 − 4 2 − x − 1 2 − x = 0
x 2 − 4 2 − x − 2 − x 2 − x = 0
x 2 − 4 − ( 2 − x ) 2 − x = 0
x 2 − 4 − 2 + x 2 − x = 0
x 2 + x − 6 2 − x = 0
Первый шаг алгоритма выполнен успешно.
Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:
x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.
a = 1, b = 1, c = − 6
D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25
D > 0 – будет два различных корня.
x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Корни, полученные на предыдущем шаге:
Значит, в ответ идет только один корень, x = − 3.
Системы уравнений
Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y ) , которые объединены в общую систему фигурной скобкой.
Пример системы уравнений
Решить систему уравнений – найти пару чисел x и y , которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.
Существует два метода решений систем линейных уравнений:
- Метод подстановки.
- Метод сложения.
Алгоритм решения системы уравнений методом подстановки:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
- Найти оставшуюся неизвестную.
Решить систему уравнений методом подстановки
Решение:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
3 ( 8 − 2 y ) − y = − 4
y = − 28 − 7 = 28 7 = 4
- Найти оставшуюся неизвестную.
x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0
Ответ можно записать одним из трех способов:
Решение системы уравнений методом сложения.
Метод сложения основывается на следующем свойстве:
Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.
Решить систему уравнений методом сложения
Давайте избавимся в данном примере от переменной x . Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3 . Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент ( − 3 ) . Для этого домножим левую и правую часть первого уравнения на ( − 3 ) .
Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.
( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )
− 3 x − 6 y + 3 x − y = − 24 − 4
y = − 28 − 7 = 28 7 = 4
Осталось найти переменную x . Для этого подставим y = 4 в любое из двух уравнений системы. Например, в первое.
Ответ можно записать одним из трех способов:
Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.
источники:
http://reshit.ru/Kak-reshat-uravneniya-s-drobyami
http://epmat.ru/modul-algebra/urok-4-uravneniya-sistemy-uravnenij/
сложи дроби
x−1×2−xy+1−yxy−y2
.
Решение:
1) знаменатели дробей раскладываем на множители:
.
2) Находим общий знаменатель:
у знаменателя первой дроби (x (x – y)), по сравнению со знаменателем второй дроби, не хватает множителя (y); поэтому общим знаменателем этих дробей является
xx−y⋅y=xyx−y
.
3) Приводим дроби к общему знаменателю, складываем их и упрощаем результат:
x−1x(x−y)+1−yy(x−y)=x−1yx(x−y)+1−yxy(x−y)=xy−y+x−yxxy(x−y)=
.
Алгебраические дроби складывают и вычитают по
правилам сложения и вычитания
обыкновенных дробей.
Сложение алгебраических дробей
Запомните!
![]()
Складывать можно только дроби с одинаковыми знаменателями!
Нельзя складывать дроби без преобразований
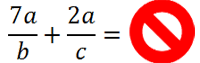
Можно складывать дроби
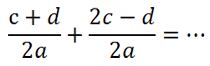
При сложении алгебраических дробей с одинаковыми знаменателями:
- числитель первой дроби складывается с числителем второй дроби;
- знаменатель остаётся прежним.
Рассмотрим пример сложения алгебраических дробей.
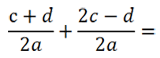
Так как знаменатель у обеих дробей «2а», значит, дроби можно сложить.
Сложим числитель первой дроби с числителем второй дроби, а знаменатель оставим прежним.
При сложении дробей в полученном числителе
приведем подобные.
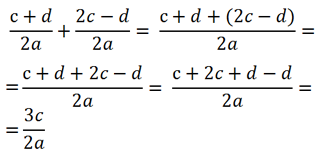
Вычитание алгебраических дробей
Запомните!
![]()
Вычитать можно только дроби с одинаковыми знаменателями!
При вычитании алгебраических дробей с одинаковыми знаменателями:
- из числителя первой дроби вычитается числитель второй дроби.
- знаменатель остаётся прежним.
Важно!

Обязательно заключите в скобки весь числитель вычитаемой дроби.
Иначе вы сделаете ошибку в знаках при раскрытии скобок вычитаемой дроби.
Рассмотрим пример вычитания алгебраических дробей.
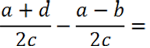
Так как у обеих алгебраических дробей знаменатель «2с», значит, эти дроби можно вычитать.
Вычтем из числителя первой дроби «(a + d)» числитель второй дроби
«(a − b)».
Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем
правило раскрытия скобок.
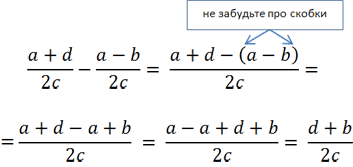
Приведение алгебраических дробей к общему знаменателю
Рассмотрим другой пример. Требуется сложить алгебраические дроби.
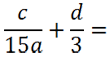
В таком виде сложить дроби нельзя, так как у них разные знаменатели.
Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю.
Правила приведения алгебраических дробей к общему знаменателю очень похожи на
правила приведения к общему знаменателю
обыкновенных дробей.
.
В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.
Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.
- Работаем с числовыми коэффициентами. Определяем
НОК
(наименьшее общее кратное) для всех числовых коэффициентов. - Работаем с многочленами. Определяем все различные многочлены в наибольших степенях.
- Произведение числового коэффициента и всех различных многочленов в наибольших степенях и будет общим знаменателем.
- Определяем, на что нужно умножить каждую алгебраическую дробь, чтобы получить общий знаменатель.
Вернемся к нашему примеру.
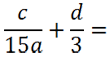
Рассмотрим знаменатели «15a» и «3» обеих дробей и найдем для них общий знаменатель.
- Работаем с числовыми коэффициентами. Находим НОК (наименьшее общее кратное — это число, которое без остатка
делится на каждый числовый коэффициент).
Для «15» и «3» — это «15». - Работаем с многочленами. Необходимо перечислить все многочлены в наибольших степенях.
В знаменателях «15a» и «5» есть только
один одночлен — «а». - Перемножим НОК из п.1 «15» и одночлен «а» из п.2. У нас получится «15a». Это и будет общим знаменателем.
- Для каждой дроби зададим себе вопрос: «На что нужно умножить знаменатель этой дроби, чтобы получить «15a»?».
Рассмотрим первую дробь. В этой дроби и так знаменатель «15a», значит, ее не требуется ни на что умножать.
Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить «3», чтобы получить «15a»?»
Ответ — на «5a».
При приведении к общему знаменателю дроби умножаем на «5a»
и числитель, и знаменатель.
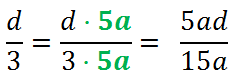
Сокращенную запись приведения алгебраической дроби к общему знаменателю можно записать через
«домики».
Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.
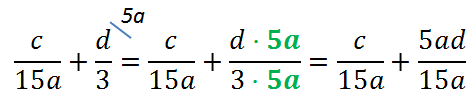
Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.
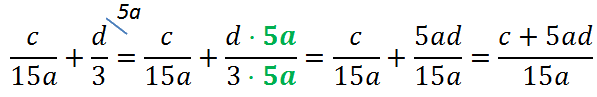
Рассмотрим пример вычитания дробей с разными знаменателями.
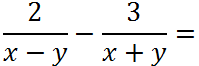
В таком виде вычитать дроби нельзя, так как у них разные знаменатели. Чтобы вычесть дроби, необходимо привести их к общему знаменателю.
Рассмотрим знаменатели «(x − y)» и «(x + y)» обеих дробей и найдем для них общий знаменатель.
- Работаем с числовыми коэффициентами. Числовых коэффициентов в знаменателях нет, поэтому переходим к многочленам.
- Работаем с многочленами. Находим все различные многочлены из знаменателей в наибольших степенях и перемножаем их.
Важно!

Многочлены необходимо рассматривать целиком!
Для удобства заключайте целый многочлен в скобки.
У нас есть два различных многочлена в знаменателях «(x − y)» и «(x + y)».
Их произведение будет общим знаменателем, т.е. «(x − y)(x + y)» — общий знаменатель.
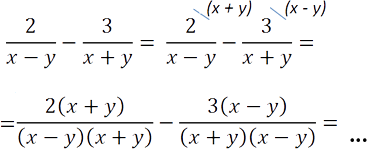
Теперь дроби можно вычитать, т.к. у них одинаковый знаменатель.
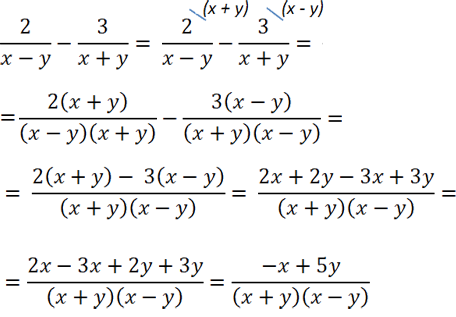
Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения
В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать
формулы сокращенного умножения.
Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.
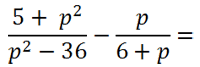
В первой алгебраической дроби знаменатель «(p2 − 36)». Очевидно, что к нему можно
применить формулу разности квадратов.
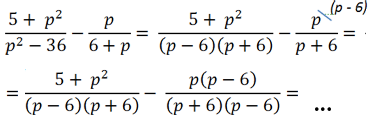
После разложения многочлена «(p2 − 36)» на произведение
многочленов
«(p + 6)(p − 6)»
видно, что в дробях повторяется многочлен «(p + 6)».
Значит, общим знаменателем дробей будет произведение многочленов «(p + 6)(p − 6)».
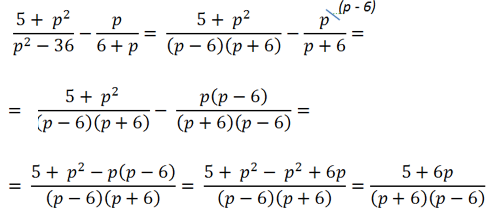
Важно!

Прежде чем приводить многочлены к общему знаменателю, попытайтесь
использовать формулы сокращённого умножения или вынесение общего множителя за скобки.
Примеры сложения и вычитания дробей с разными знаменателями с использованием формул сокращенного умножения.
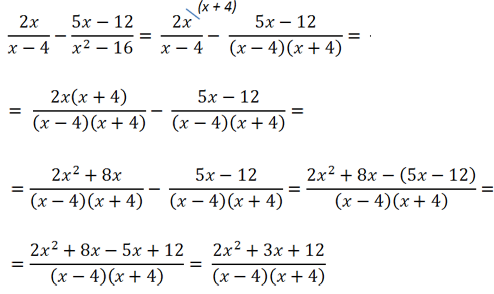
Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки
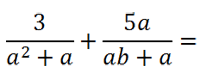
На первый взгляд одинаковых многочленов в обеих дробях нет.
Вынесем общий множитель
«а» за скобки в обоих знаменателях.
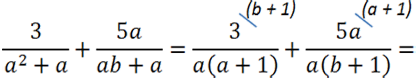
После вынесения общего множителя «а» за скобки, в
обоих знаменателях появился одинаковый одночлен «а».
Значит, общий знаменатель для обеих дробей будет выглядеть так: «а(а + 1)(b + 1)».

Сложение алгебраической дроби с одночленом или числом
Рассмотрим пример. Требуется сложить алгебраическую дробь с одночленом (буквой).
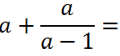
Чтобы сложить одночлен или число с алгебраической дробью,
нужно представить одночлен в виде дроби со знаменателем «1».
Представим одночлен «а» как алгебраическую дробь со знаменателем «1».
Подобное действие можно сделать, так как при делении на единицу получается тот же самый одночлен.
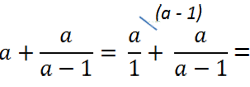
Теперь приведем алгебраические дроби к общему знаменателю «(а − 1)» и решим пример.
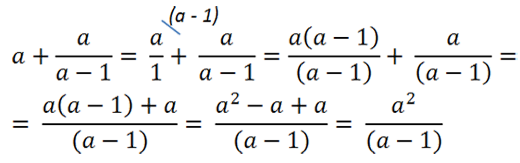
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Линейные уравнения с дробями не содержат переменной в знаменателе. Чтобы решить линейное уравнение с дробями, удобно избавиться от знаменателей.
Для этого нужно найти наименьший общий знаменатель всех входящих в уравнение дробей и обе части уравнения умножить на это число.
![]()
Наименьший общий знаменатель данных дробей равен 6. Дополнительный множитель к первой дроби равен 2, ко второй — 3, к 5 — 6. Умножаем обе части уравнения на наименьший общий знаменатель:
Можно, конечно, сразу же умножить дополнительный множитель на числитель каждой дроби. Но, к сожалению, наибольшее количество ошибок при решении линейных уравнений с дробями допускается именно на этом шаге. Скобки — друзья ученика :). Поэтому лучше воспользоваться их помощью:
-

- Особенно полезны скобки в случае, когда перед дробью стоит знак «минус».
- После раскрытия скобок можно сразу же перенести неизвестные в одну сторону уравнения, известные — в другую (не забыв при переносе изменить их знаки), а можно сначала упростить каждую часть, приведя подобные слагаемые, а потом уже переносить.
- Ответ: -34.
- Здесь наименьший общий знаменатель дробей равен 12. Находим дополнительный множитель к каждой дроби и умножаем обе части уравнения на 12:
- Раскрываем скобки и упрощаем
- Обе части уравнения делим на число, стоящее перед иксом:
- Ответ: -5.
- Уравнения такого вида можно решить, использовать основное свойство пропорции (в верной пропорции произведение крайних членов равно произведению средних членов):
- при делении двух отрицательных чисел получается положительное число, поэтому минусы можно сразу же не писать.
- Если это возможно, лучше ответ записать в виде десятичной дроби:
- Ответ: 0,1875.
Источник: http://www.algebraclass.ru/linejnye-uravneniya-s-drobyami/
Матвокс ⋆ решение дробных уравнений. пример 8 ⋆ энциклопедия математики
Для решения этого уравнения не будем применять основное свойство пропорций.
Перенесем все в левую часть уравнения:

- На этом шаге нужно приводить все слагаемые к общему знаменателю.
- Если внимательно посмотреть на знаменатели дробей, то можно увидеть, что один из них – это квадратный трехчлен.
- В таких ситуациях нужно всегда пытаться разложить его на множители, так как это может позволить упростить поиск общего знаменателя.
- Таким образом, разложим на множители:

Для этого приравняем к нулю и решим полученное квадратное уравнение:
Найдем дискриминант:

Корнями квадратного уравнения будут:

И:

Разложим уравнение на множители:

Уравнение примет вид:

Очевидно, данное разложение на множители сильно упростило дальнейшие вычисления.
Приведем слагаемые к общему знаменателю и запишем в виде одной дроби:
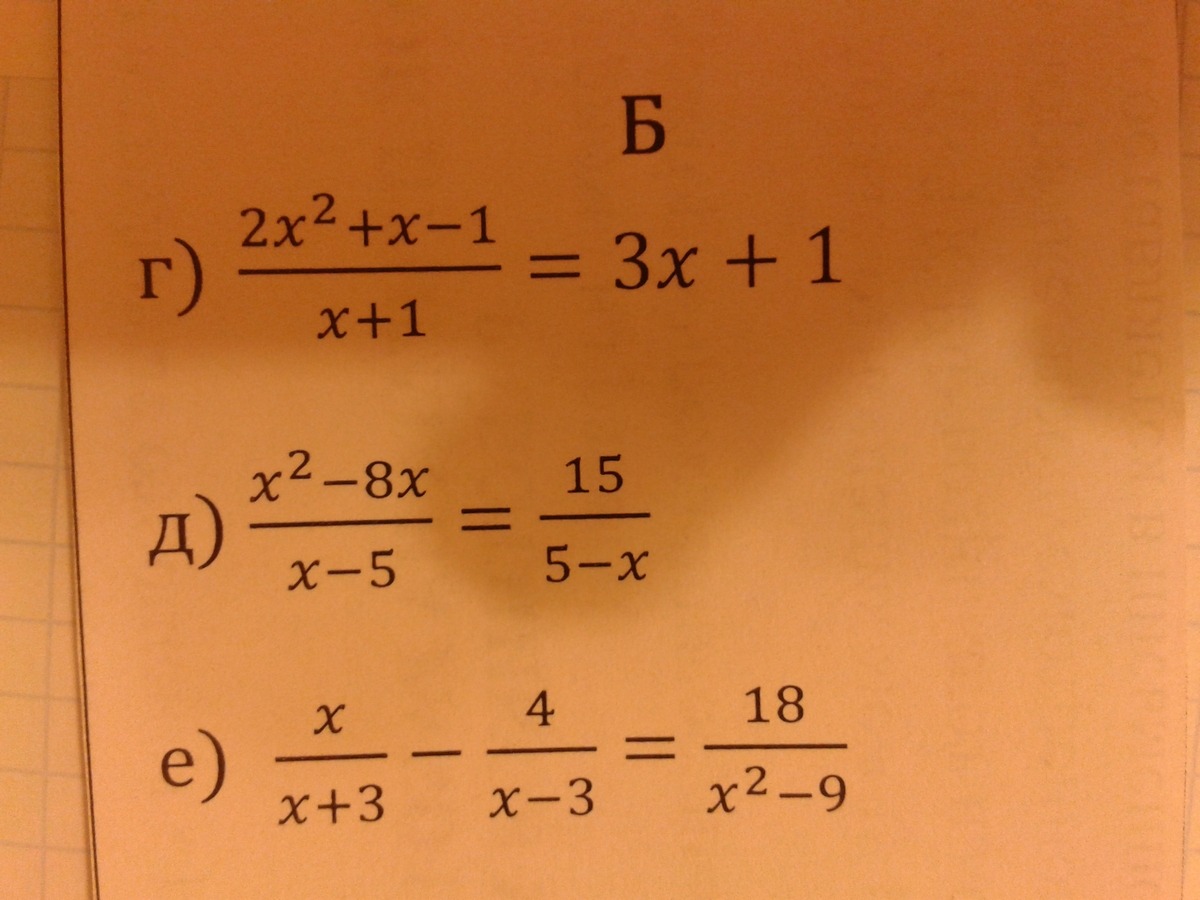
Отсюда:

- Упростим:
- Отсюда:
В числителе записано выражение, а не число, значит переходим к шагу 7.
- Приравняем числитель к нулю и решим полученное уравнение:
- Так как можно все элементы уравнения делить на любое число, отличное от нуля, то разделим их на -2:
- Это квадратное уравнение. Решим его с помощью дискриминанта:
- Корнями квадратного уравнения будут:
- и
- Полученные корни не сложные для дальнейших вычислений, и, если посмотреть на знаменатель, то и он не сложный для нахождения ОДЗ.
- Поэтому в данном случае можно выбрать любой из вариантов алгоритма.
Найдем ОДЗ изначального уравнения. Поэтому переходим к шагу 9 алгоритма.
- Найдем значения, при которых знаменатель изначального уравнения не равен нулю:
- Произведение не равно нулю, когда каждый из множителей не равен нулю:
- Отсюда:
- На этом шаге выберем корни уравнения, полученные на шаге 7, попадающие в ОДЗ.
- Итак:
- и
- При этом:
- и
- Таким образом, корень, равный -2 не попадает в ОДЗ, и значит его нужно исключить из ответа.
Можно провести проверку корня.
- Ответ:
- Корень дробного уравнения равен 1:
Источник: https://mathvox.ru/algebra/uravneniya-reshenie-uravnenii/glava-3-drobnie-uravneniya/reshenie-drobnih-uravnenii-primer-8/
Как решать уравнения с дробями. Показательное решение уравнений с дробями
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
- Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45 - x=45-20=25
- Другой пример, когда неизвестное находится в знаменателе:
- b/x + c = d
- Уравнения такого типа называются дробно-рациональными или просто дробными.
- Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:
- значение переменной, обращающее в 0 знаменатель, корнем быть не может;
- нельзя делить или умножать уравнение на выражение =0.
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
1/x + 2 = 5
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
- Избавляемся от знаменателя путем умножения всех членов уравнения на х
- 1 + 2x = 5х
- И решаем обычное уравнение
- 5x – 2х = 1
3x = 1 - х = 1/3
- Ответ: х = 1/3
- Решим уравнение посложнее:
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):

Это самое обычное умножение дробей, которое мы уже рассмотрели выше

Запишем это же уравнение, но несколько по-другому

- Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
- 4 = х + 2
- х = 4 – 2 = 2, что соответствует нашей ОДЗ
- Ответ: х = 2.
- Для закрепления материала рекомендуем еще посмотреть видео.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в х.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Источник: https://reshit.ru/Kak-reshat-uravneniya-s-drobyami
Уравнение неизвестный числитель дроби. Как решать уравнения с дробями по математике
Уравнение — это равенство, содержащее букву, значение которой надо найти.
В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы « x » [икс] и « y » [игрек].
— это значение буквы, при котором из уравнения получается верное числовое равенство.
— значит найти все его корни или убедиться, что корней нет.
Решив уравнение, всегда после ответа записываем проверку.
Информация для родителей
Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа».
Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.
Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.
Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке «Законы арифметики».
Решение уравнений на сложение и вычитание
- Как найти неизвестноеслагаемое
- Как найти неизвестноеуменьшаемое
- Как найти неизвестноевычитаемое
- Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
- Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
- x + 9 = 15x = 15 − 9x = 6
- Проверка
- x − 14 = 2x = 14 + 2x = 16
- Проверка
- 16 − 2 = 1414 = 14
- 5 − x = 3x = 5 − 3x = 2
- Проверка
Решение уравнений на умножение и деление
- Как найти неизвестныймножитель
- Как найти неизвестноеделимое
- Как найти неизвестныйделитель
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
- Чтобы найти неизвестное делимое, надо частное умножить на делитель.
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
- y · 4 = 12y = 12: 4y = 3
- Проверка
- y: 7 = 2y = 2 · 7y = 14
- Проверка
- 8: y = 4y = 8: 4y = 2
- Проверка
- Уравнение — это равенство, содержащее букву, знамение которой нужно найти.
Решение уравнения — это тот набор значений букв, при котором уравнение превращается в верное равенство:
- Напомним, что для решения уравнении
надо слагаемые с неизвестным перенести в одну часть равенства, а числовые слагаемые в другую, привести подобные и получить такое равенство: - Из последнего равенства определим неизвестное по правилу: «один из множителей равен частному, деленному на второй множитель».
- Так как рациональные числа а и Ь могут иметь одинаковые и разные знаки, то знак неизвестного определяется по правилам деления рациональных чисел.
Порядок решения линейных уравнений
- Линейное уравнение необходимо упростить, раскрыв скобки и выполнив действия второй ступени (умножение и деление).
- Перенести неизвестные в одну сторону от знака равенства, а числа — в другую сторону от знака равенства, получив тождественное заданному равенство,
- Привести подобные слева и справа от знака равенства, получив равенство вида ax
= b
. - Вычислить корень уравнения (найти неизвестное х
из равенства x
= b
: a
), - Выполнить проверку, подставив неизвестное в заданное уравнение.
- Если получим тождество в числовом равенстве, то уравнение решено верно.
Особые случаи решения уравнений
- Если уравнение
задано произведением, равным 0, то для его решения используем свойство умножения: «произведение равно нулю, если один из сомножителей или оба сомножителя равны нулю».
- 27 (x
— 3) = 0 27 не равно 0, значит x
— 3 = 0 - У второго примера два решения уравнения, так как это уравнение второй степени:
- Если коэффициенты уравнения являются обыкновенными дробями, то прежде всего надо избавиться от знаменателей.
Для этого:
- Найти общий знаменатель;
- Определить дополнительные множители для каждого члена уравнения;
- Умножить числители дробей и целые числа на дополнительные множители и записать все члены уравнения без знаменателей (общий знаменатель можно отбросить);
- Перенести слагаемые с неизвестными в одну часть уравнения, а числовые слагаемые — в другую от знака равенства, получив равносильное равенство;
- Привести подобные члены;
Основные свойства уравнений
- В любой части уравнения можно приводить подобные слагаемые или раскрывать скобку.
- Любой член уравнения можно переносить из одной части уравнения в другую, изменив его знак на противоположный.
- Обе части уравнения можно умножать (делить) на одно и то же число, кроме 0.
- В примере выше для решения уравнения были использованы все его свойства.
Как решить уравнение с неизвестным в дроби
Иногда линейные уравнения принимают вид, когда неизвестное
оказывается в числителе одной или нескольких дробей. Как, например, в уравнении ниже.
В таких случаях подобные уравнения можно решить двумя способами.
I способ решения Сведение уравнения к пропорции
При решении уравнений способом пропорции необходимо выполнить следующие действия:
Итак, вернемся к нашему уравнению. В левой части у нас и так стоит только одна дробь, поэтому в ней не нужны никакие преобразования.
Будем работать с правой частью уравнения. Упростим правую часть уравнения так, чтобы там осталась только одна дробь. Для этого вспомним правила сложения числа с алгебраической дробью.

Теперь используем правило пропорции и решим уравнение до конца.
Источник: https://svfan.ru/uravnenie-neizvestnyi-chislitel-drobi-kak-reshat-uravneniya-s-drobyami-po/
Действия с дробями 7 класс, повторение, сравнение, сокращение, решение уравнений
В начале первой четверти семиклассники на уроках математики активно повторяют все действия, как с обыкновенными, так и с десятичными дробями. И делают они это не просто так.
В 7 классе по программе обучения начинается алгебра. Дроби будут состоять уже из алгебраических выражений, многочленов. Все действия с такими уже дробями основываются на умении решать обыкновенные дроби в пятом шестом классе.
Дроби повторение 7 класс
Повторение начинается с самых простых примеров на все арифметические действия с обыкновенными дробями. Не забываем, что там где знаменатели разные следует найти общий, и только потом выполнять действия.
Сравнение дробей 7 класс
Для того, чтобы научиться сравнивать дроби, нужно узнать несколько способов по их сравнению, и выбрать для себя более понятный и удобный.
Основные правила сравнения дробей:
В первом правиле мы сравниваем только числители, так как знаменатели равны. Мы уже говорили, что знамен.-это общее количество долей, а числитель показывает сколько их взято из общего, следовательно, чем больше долей взято, тем и дробь соответственно больше.
При одинаковых числ-х сравнивают только знамен. Чем он меньше, тем больше дробь. Разберемся, почему так. К примеру разделите 10 на 5 и 10 на 2, очевидно, что второе частное больше первого. Поэтому, если сравнить 10/5 и 10/2, то 10/2 будет больше.
В десятичных дробях мы сравниваем их соответствующие целые части и дробные. Если первые равны, то мы сравниваем десятые, сотые и т.д. Поэтому для сравнения мы должны уравнивать количество дес.знаков.
Также можно сравнить две обыкн.дроби используя число, которое находится в ряду между ними. Какая из дробей окажется больше этого числа, та и будет большей в примере.
Вот несколько интересных способов, как можно сравнить дроби:
Если от вас требуется сравнить десятичную и обыкновенную дроби, можно перевести одну из них в более удобную для вас. И сравнивать вы уже будите либо обыкновенные, либо десятичные.
Еще один хороший способ, дополнить до единицы. Чем больше нужно добавить дроби, чтобы получить целое, тем она будет меньше.
Можно использовать и перекрестное правило, как в пропорции. Для этого умножаем смотрящие друг на друга числители и знаменатели.
Правила дробей 7 класс
- Начиная изучать рациональные дроби в седьмом классе, стоит познакомиться с рядом правил, которым подчиняются действия с ними.
- К рациональным дробям применяются те же правила, что и к обыкн-м.
- Для выполнения всех арифметических действий, следует знать несколько формул сокращенного умножения:
- Эти формулы понадобятся на уроках математики до 11 класса, поэтому их лучше выучить сразу в седьмом.
Действия с дробями 7 класс
Как в пятом и шестом, так же и в седьмом классе, дроби в основном складывают, вычитают, умножают и делят. Есть еще сокращение и сравнение. Рациональные дроби также называют алгебраическими.
Сложение и вычитание.
К примеру, b/3 + c/3. Это сумма рациональных или алгебраических дробей. Решением будет: b+c/3.
Еще пара примеров.
Умножение и деление.
Так же как и с обыкновенными дробями, умножать будем числитель на числитель, и знам. на знаменатель. Очень важно обратить внимание на то, что вы умножаете многочлены, поэтому каждый числитель и знаменатель лучше взять в скобки. Так вы сможете избежать ненужных ошибок.
И деление выполняется в точности также как и в обык.дробях. Первую дробь оставьте на месте без изменений, поменяйте частное на умножение, вторую дробь переверните.
Сложение и вычитание дробей 7 класс
Никогда не начинайте выполнять действия не упростив выражения. Выполните все возможные преобразования и пример решится намного легче и быстрее. Также числители второй и последующих дробей при сложении и вычитании стоит взять в скобки. Очень часто возникают ошибки только из-за одного неправильно поставленного знака. Будьте внимательны.
Если перед скобкой стоит , раскрываем ее, не меняя знаки внутри. Если >, то все меняем на противоположные.
Пример.
Знаменатели совершенно одинаковые, находим сумму числ. Приведите подобные, это с и 2с, d и -d, которые в свою очередь взаимно уничтожаются, так как имеют разные знаки. В итоге остается с+2с = 3с. Ответ: 3с/2а.
Все намного проще, если знам. одинаковые. С разными нужно немного подумать.
Пример.
В примере два знам. 15а и 3. Нам нужно найти общий. В этом случае проще домножить 3 так, чтобы получить 15а. Для этого 3 умножаем на 5а. Но чтобы действие было верным, применяем основное свойство дроби, и на 5а умножим еще и числитель. Далее складываем дроби с один.знам.
Деление и умножение дробей 7 класс
Разберем сразу примеры, так как правила уже обговорены выше.
В примере выше требуется разделить алгебраические дроби, содержащие выражения со степенью. Здесь важно вспомнить, что при сокращении степеней мы вычитаем из большей степени меньшую.
Первую дробь мы оставили без изменений, вторую перевернули, заменив действие на умножение. Теперь ищем, что можно сократить. Сначала смотри на числовые коэффициенты. Сокращаем 7 и 35, 9 и 18. Затем сокращаем буквенную часть.
Для удобства возьмите каждый многочлен в скобки. Мы видим, что сразу можно сократить скобку (7-х). Многие допускают ошибку, считая что (a-b) и (a+b) сократимы, это большая ошибка. Ведь к примеру, 5-2 и 5+2 совершенно разные выражения.
Конечные десятичные дроби 7 класс
Десятичные дроби отличаются друг от друга по количеству знаков (цифр) после запятой. Соответственно своему названию, у конечной десятичной дроби после запятой, конечное число знаков: 5, 0235; 2,3654; 0,12 и т.д.
Любую такую дробь можно перевести обратно в обыкновенную. 2,36 = 2 целых 36/100. Но не каждую обыкновенную можно представить в виде конечной дес.дроби. В таком случае уже получается бесконечная дес.дробь.
Уравнения с дробями 7 класс на примерах с пояснением
Уравнения с дробями можно решить используя пропорцию, или светси решение к этому. Первое уравнение и ему подобные очень просто и быстро решается пропорцией. Используем умножение .
Бывают и более сложные уравнения, которые нужно преобразовать.
Здесь уже нужно вспомнить правило умножения скобки на число или раскрытие скобок. На число перед скобкой умножаем каждое слагаемое в скобке. Значит 7 умножим и на 2, и на (-х). Далее решаем как обычное линейное уравнение.
В следующем уравнении разберем два способа решения.
Первый вариант решения основывается на избавлении от знаменателей, дабы превратить дробное уравнение в линейное. Для этого умножаем каждое слагаемое на общий для дробей знаменатель. В нашем случае 45.
Сокращаем и получаем линейное уравнение. Раскрываем в нем скобки, находим подобные слагаемые.
Вторым вариантом будет приведение к общему знаменателю в правой части, и сведению решения к пропорции.
Сокращение дробей 7 класс
При сокращении рациональных дробей используем правило сокращения обык.др. Числитель и знаменатель делим на один многочлен.
Запомните, что разные буквенные части мы не сокращаем, только одинаковые.
Дроби, в числ. и знамен. которых стоит выражение (многочлен) тоже сократимы. В таких дробях можно сокращать только одинаковые многочлены. Многочлены разделены между собой умножением.
Также можно использовать формулы сокращ. умножения.
Еще пара примеров:
Источник: https://luckclub.ru/dejstviya-s-drobyami-7-klass-povtorenie-sravnenie-sokrashhenie-reshenie-uravnenij
10 Методы решения уравнений, содержащих целые или дробные части
К
числу нестандартных относятся методы
решения уравнений, которые содержат
целые и (или) дробные части действительных
чисел. В программе школьной математики
методы решения таких уравнений не
изучаются. В настоящем разделе применение
существующих методов и приемов
иллюстрируется на примерах решения
ряда уравнений.
Целой
частью действительного числа (илиАнтье)
называется
наибольшее целое число, не превосходящее
,
и это число обозначается.
Очевидно, что
png»>Разностьназывается дробной частью числа(илиМантисса)
и
обозначается через Из определения следует, что
png»>Кроме того, справедливо равенство
Отметим
некоторые свойства введенного выше
понятия целой части действительного
числа.
Перейдем
теперь к рассмотрению уравнений,
содержащих целую и (или) дробную части
неизвестной переменной.
Задачи
и решений
Пример
10.1. Решить
уравнение
Решение.
Поскольку
являются целым числом, то- тоже целое число. Следовательно, число
png»>также является целым. В таком случаеи уравнение (10.3) принимает видЦелыми корнями последнего уравнения
являются
qmhj/img-Aj5vlr.png»>
Пример
10.2. Решить
уравнение
Решение.
Рассмотрим
последовательно три случая.
Если
,
т.е. решением уравнения (10.4) могут быть
только
Пусть
тогда из уравнения (10.4) следует, чтоТак
как,
то получаем систему неравенств
Если
Следовательно, уравнение (10.4) не имеет
корней среди
Пример
10.3. Решить
уравнение
Решение.
Используя
свойство (10.2), можно записать
Отсюда,
принимая во внимание уравнение (10.5),
следуют неравенства
Поскольку
в этом случае следует,
что.
Так как- целое число, то отсюда получаем, что
png»>Следовательно, имеем
Из
уравнения (10.5) следует, что – целое число. Так как
png»>то остается лишь проверить целые значенияНетрудно установить, что решениями
(10.5) являются
qmhj/img-kYkNrI.png»>
Пример
10.4. Решить
уравнение
(10.7)
Решение.
Из
формулы (10.1) следует, что В этой связи уравнение (10.7) можно
переписать, как
Отсюда
следует уравнение
(10.8)
Очевидно,
что является корнем уравнения (10.8). Положим,
чтоТогда разделим обе части уравнения
(10.9) наи получим уравнение
Рассмотрим
последовательно несколько случаем.
Если
В таком случае
Пример
10.5. Решить
уравнение
Решение.
Решая
тригонометрическое уравнение (10.10),
получаем
(10.11)
где
– целое число. Из уравнения (10.11) получаем
совокупность двух уравнений
png»>Левые части обоих уравнений являются
целыми числами, в то время как их правые
части (за исключением случая
png»>в первом уравнении) принимают иррациональные
значения.
Следовательно,
равенство в уравнениях совокупности
может иметь место только в том случае,
когда правые их части являются
рациональными (точнее, целыми) числами.
А это возможно лишь в первом уравнении
при условии, что В этом случае получаем уравнение
png»>откуда следует
Ответ:
Пример
10.6. Решить
уравнение
Решение.
Левая
часть уравнения (10.12) принимает только
целые значения, поэтому число является целым.
Так
как то при любом целоммногочленпредставляет собой произведение трех
последовательно расположенных на
числовой оси
qmhj/img-b1a3G_.png»>целых чисел, среди которых имеется хотя
бы одно четное число и число, кратное
трем. Следовательно, многочленделится набез остатка, т.е.
png»>является целым числом.
В
этой связи и уравнение (10.12) принимает видили
Так
как то корнями уравнения (10.13) являются
Ответ:
Пример
10.7. Доказать
равенство
Доказательство.
Любое число можно представить или какгде- целое число и
Рассмотрим
два возможных случая.
-
Пусть Так как
Таким
образом, равенство (10.14) выполняется для
каждого из двух рассмотренных выше
случаем. Следовательно, равенство
(10.14) доказано.
Заключение
В
результате работы над дипломным проектом
был проведен анализ решения нестандартных
типов решения тестовых задач. Все
рассмотренные задачи, решаемые
нестандартными методами, классифицированы
по следующим типам:
-
метод функциональной подстановки
-
методы, основанные на применении численных неравенств,
-
метод тригонометрической подстановки;
-
методы, основанные на монотонности функций,
-
методы решения функциональных уравнений,
-
методы, основанные на применении векторов,
-
комбинированные методы,
-
методы, основанные на использовании ограниченности функций,
-
методы решения симметрических систем уравнений,
-
методы решения уравнений, содержащих целые или дробные части числа.
-
В
каждом из этих типов рассмотрены
конкретные примеры и методы их решения. -
Материал,
содержащийся в дипломной работе,
представляет собой основу методического
пособия, которое можно при определенной
доработке, внедрять как в школьный
процесс, так и при подготовке абитуриентов
к поступлению. -
Список
использованных источников
-
Азаров, В.И. Функциональные методы решения задач [текст] : учебное пособие / В.И. Азаров, О.П. Тавгень, В.С. Федосенко. – Мн. :БГУ,1994.
-
Азаров, А.И Экзамен по математике: руководство к решению задач [текст] : справочное пособие / С.В. Пруцко, В.С. Федосенко. – Мн. :ТетраСистем, 2001.
-
Ивлев, Б.М. Задачи повышенной трудности по алгебре и началам анализа [текст] : учебное пособие / Б.М. Ивлев, А.М.Абрамов, Ю.П. Дудницин, С.И. Шварцбург. -М. :Просвещение, 1990.
-
Габринович, В.А. Решим любую задачу [текст] : учебное пособие / В.А. Габринович, В.И. Громак. – Мн. :Асар, 1996.
-
Мандрик, П.А. Экзамен по математике на пять [текст] : учебное пособие / П.А. Мандрик, В.И. Репников. – Мн. :тетраСистемс, 1999.
-
Олехник, С.Н. Нестандартные методы решений уравнений и неравенств [текст] : учебное пособие / С.Н. Олехник, М.К. Потапов, П.И. Пасаиченуо. – М. :МГУ, 1991.
-
Пруцко, С.В. Экзамен по математике [текст] : руководство к решению задач : учебное пособие / С.В. Пруцко, А.И. Азаров, В.С. Федосенко. – МН. :тетраСистемс, 2001.
-
Пруцко, С.В. руководство к решению конкурсных задач по математике [текст] : учебное пособие / С.В. Пруцко, А.И. Азаров, В.С. Федосенко. – МН. :тетраСистемс, 1999.
-
Сборник задач по математике для поступающих во втузы [текст] / под редакцией М.И.Сканави. – Мн. :Высшая школа, 1990.
-
Супрун, В.П. Избранные задачи повышенной сложности по математике [текст] / В.П. Супрун. Мн. :Полымя, 1998.
-
Супрун, В.П. Нестандартные методы решения задач по математике [текст] / В.П. Супрун. –Мн. :Полымя, 2000.
Источник: https://studfile.net/preview/5792561/page:8/
