Содержание:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
- Сложение смешанных дробей
Сложение дробей с одинаковыми знаменателями
Определение
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме
числителей исходных дробей, а знаменатель – знаменателю дробей, то есть
$frac{a}{b}+frac{c}{b}=frac{a+c}{b}$
Чтобы сложить две дроби с одинаковым знаменателем, надо сложить
их числители и результат записать в числитель, а
знаменатель оставить без изменения.
Пример
Задание. Найти сумму дробей
$frac{3}{11}$ и
$frac{7}{11}$
Решение. $frac{3}{11}+frac{7}{11}=frac{3+7}{11}=frac{10}{11}$
Ответ. $frac{3}{11}+frac{7}{11}=frac{10}{11}$
Если в результате сложения получается дробь, числитель и знаменатель которой можно сократить,
то для конечного результата выполняем и сокращение дроби.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму дробей
$frac{3}{14}$ и
$frac{11}{14}$
Решение. Складываются дроби с одинаковым знаменателем,
поэтому просто складываем числитель, а знаменатель оставляем исходный:
$frac{3}{14}+frac{11}{14}=frac{14}{14}$
Полученная дробь $frac{14}{14}$ является
неправильной, у которой числитель равен знаменателю, и такая дробь равна единице, то есть
$frac{3}{14}+frac{11}{14}=frac{14}{14}=1$
Ответ. $frac{3}{14}+frac{11}{14}=1$
Сложение дробей с разными знаменателями
Определение
Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а
далее складывать как дроби с общим знаменателем.
Пример
Задание. Сложить дроби
$frac{2}{3}$ и
$frac{1}{8}$
Решение. Так как дроби с разными знаменателями, то вначале приведем их к
наименьшему общему знаменателю. Для этого найдем НОК чисел 3 и 8:
НОК (3, 8) = 24
Дополнительные множители к каждой из дробей соответственно:
$24 : 3=8,24 : 8=3$
то есть
$frac{2}{3}+frac{1}{8}=frac{2^{8}}{3}+frac{1^{3}}{8}=frac{2 cdot 8+1 cdot 3}{24}=frac{16+3}{24}=frac{19}{24}$
Ответ. $frac{2}{3}+frac{1}{8}=frac{19}{24}$
Замечание. После первого знака равенства справа вверху у каждой дроби указан дополнительный множитель к ней.
Сложение смешанных дробей
Определение
Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.
Пример
Задание. Вычислить сумму дробей
3$frac{2}{5}$ и
4$frac{7}{10}$
Решение. В данном случае складываем отдельно целые и дробные части:
$3 frac{2}{5}+4 frac{7}{10}=(3+4)+left(frac{2}{5}+frac{7}{10}right)$
Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 10, так как НОК
знаменателей 5 и 10. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 2 и 1:
$3 frac{2}{5}+4 frac{7}{10}=7+frac{2^{2}}{5}+frac{7^{1}}{10}=7+frac{2 cdot 2+7 cdot 1}{10}=7+frac{11}{10}=7 frac{11}{10}$
Так как дробная часть представляет собой
неправильную дробь, то выделяем целую часть:
$3 frac{2}{5}+4 frac{7}{10}=7 frac{11}{10}=7left(1+frac{1}{10}right)=8 frac{1}{10}$
Ответ. $3 frac{2}{5}+4 frac{7}{10}=8 frac{1}{10}$
Читать следующую тему: вычитание дробей.
Тема дроби объяснение.
Чему равна дробь, числитель которой равен знаменателю? Как сравнивать, складывать, вычитать и умножать дроби с одинаковыми числителем и знаменателем?
Рассмотрим на примерах дроби с одинаковыми числителем и знаменателем.
Проработайте примеры дробей внимательно.
Чему равна дробь, числитель которой равен знаменателю?
Дробь числитель которой равен знаменателю равна единице.
Пример.
Почему дробь, числитель которой равен знаменателю, равна единице?
Дробь – это другой способ записи деления. Смотрите в Дроби объяснение.
Значит дробь мы можем представить в виде деления:
Сравнение дробей с одинаковыми числителями и знаменателями
Дроби с одинаковыми числителями и знаменателями всегда равны.
Сложение дробей с одинаковыми знаменателями и числителями
Сложение дробей с одинаковыми знаменателями и числителями делается так: числители складываются, а знаменатель остается неизменным.
Пример.
| 5 | + | 5 | = | 5 + 5 | = | 10 | = 2 |
|---|---|---|---|---|---|---|---|
| 5 | 5 | 5 | 5 |
Вычитание дробей с одинаковыми числителями и знаменателями
Вычитание дробей с одинаковыми числителями и знаменателями всегда дает ноль.
Пример.
Умножение дробей с одинаковыми знаменателями и числителями
Умножение дробей с одинаковыми знаменателями и числителями всегда дает единицу.
Пример.
Я конечно знаю, что для сложения простые дроби надо свести к общему знаменателю. В противном случае это будет также глупо и бессмысленно, как пытаться складывать километры и литры, ибо они не будут иметь ничего общего. Не зря ведь дроби сводят к общему знаменателю еще и тогда, когда хотят их сравнить.
Однако, дроби еще могут иметь общий числитель. И тогда их тоже можно сравнить. А раз их можно сравнить, то не было бы логичным предположить, что должен существовать способ сложить(а также вычитать, умножать, делить) их? Разумеется, без приведения к общему знаменателю.
Данная мысль пришла мне сейчас в голову, когда я решал одну задачу. Изначально пример был сложней, но мне удалось преобразовать его в более простой. А именно:
5/9 + 5/12 + 5/18
Я сначала сложил 5/9 и 5/18, получилось 5/6. Потом сложил 5/6 и 5/12, получилось 5/4.
Неужели это все просто чистое совпадения(или как вариант, небольшая шутка автора. А сами числа были найдены вслепую) и тут в принципе не может быть никакой закономерности?
Сложение дробей
Сложение дробей с одинаковыми знаменателями:
Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.
Формула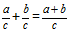 
Сложим две дроби с одинаковым с одинаковыми знаменателями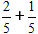 
По формуле складываем числители, а знаменатель оставляем исходный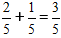 
Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.
Пример: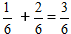 
При сокращении дроби у нас получится число 1/2
Сложение дробей с разными знаменателями:
Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.
Задача: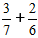 
Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК – наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение: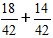 
2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21
Сложение дроби и целого числа:
Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.
Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби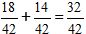 
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.
Пример: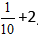 
Решение: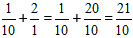 
Вычисляем целую часть, и получаем ответ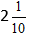 
Сложение смешанных дробей:
Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.
Формула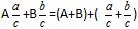 
Пример: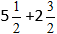 
Подставляем цифры в формулу: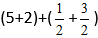 
Получаем: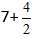 
Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.
Сложение дробей с помощью онлайн калькулятора:
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель – знаменателю дробей, то есть ab+cb=a+bcfrac{a}{b} + frac{c}{b} = frac{a+b}{c}.
Сложение дробей с одинаковыми знаменателями
Чтобы сложить две дроби с одинаковым знаменателем, надо сложить их числители и результат записать в числитель, а знаменатель оставить без изменения.
Примеры решения задач
Задание
Найти сумму дробей 513frac{5}{13} и 113.frac{1}{13}.
Решение
513+113=613frac{5}{13} + frac{1}{13} = frac{6}{13}
Задание
Найти сумму дробей 512frac{5}{12} и 112frac{1}{12}.
Решение
Складываются дроби с одинаковым знаменателем, поэтому просто складываем числитель, а знаменатель оставляем исходный:
512+112=612frac{5}{12} + frac{1}{12} = frac{6}{12}.
Полученную можно упростить – путем сокращения числителя и знаменателя на 6, то есть 512+112=612=12frac{5}{12} + frac{1}{12} = frac{6}{12} = frac {1}{2}.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а далее складывать как дроби с общим знаменателем.
Пример решения задачи
Задание
Сложить дроби 13frac{1}{3} и 12frac{1}{2}.
Решение
Так как дроби с разными знаменателями, то вначале приведем их к наименьшему общему знаменателю. Для этого найдем НОК чисел 2 и 3:
НОК (3, 2) = 6
Дополнительные множители к каждой из дробей соответственно: 6:3=2, 6:2=3, то есть
13+12=26+36=2+36=56.frac{1}{3} + frac{1}{2} = frac{2}{6} + frac{3}{6} = frac{2+3}{6} = frac{5}{6}.
Сложение смешанных дробей
Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.
Пример решения задачи
Задание
Вычислить сумму дробей 2122frac{1}{2} и 3133frac{1}{3}.
Решение
В данном случае складываем отдельно целые и дробные части:
212+313=(2+3)+(12+13).2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}).
Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 6. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 3 и 2:
212+313=(2+3)+(12+13)=2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}) =
=5+(36+26)=5+56=556.= 5 +(frac{3}{6} +frac{2}{6}) = 5+frac{5}{6} = 5 frac{5}{6}.
На нашем сайте вы можете заказать задачу по алгебре недорого от опытных исполнителей!
