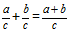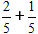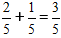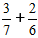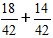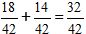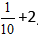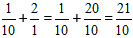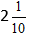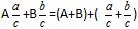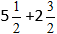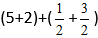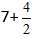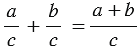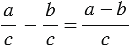Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
-
Числовые — состоят из чисел, например, 5/9 или (1,5 − 0,2)/15.
-
Алгебраические — состоят из переменных, например, (x + y)/(x − y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной называют такую дробь, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1/4.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.
- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить сумму двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное знаменателей (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в произведении дают значения знаменателей складываемых дробей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 × 2 × 3 × 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
- 90 : 15 = 6,
- 90 : 18 = 5.
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, тренируйтесь решать примеры на сложение дробей как можно чаще.
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель – знаменателю дробей, то есть ab+cb=a+bcfrac{a}{b} + frac{c}{b} = frac{a+b}{c}.
Сложение дробей с одинаковыми знаменателями
Чтобы сложить две дроби с одинаковым знаменателем, надо сложить их числители и результат записать в числитель, а знаменатель оставить без изменения.
Примеры решения задач
Задание
Найти сумму дробей 513frac{5}{13} и 113.frac{1}{13}.
Решение
513+113=613frac{5}{13} + frac{1}{13} = frac{6}{13}
Задание
Найти сумму дробей 512frac{5}{12} и 112frac{1}{12}.
Решение
Складываются дроби с одинаковым знаменателем, поэтому просто складываем числитель, а знаменатель оставляем исходный:
512+112=612frac{5}{12} + frac{1}{12} = frac{6}{12}.
Полученную можно упростить – путем сокращения числителя и знаменателя на 6, то есть 512+112=612=12frac{5}{12} + frac{1}{12} = frac{6}{12} = frac {1}{2}.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а далее складывать как дроби с общим знаменателем.
Пример решения задачи
Задание
Сложить дроби 13frac{1}{3} и 12frac{1}{2}.
Решение
Так как дроби с разными знаменателями, то вначале приведем их к наименьшему общему знаменателю. Для этого найдем НОК чисел 2 и 3:
НОК (3, 2) = 6
Дополнительные множители к каждой из дробей соответственно: 6:3=2, 6:2=3, то есть
13+12=26+36=2+36=56.frac{1}{3} + frac{1}{2} = frac{2}{6} + frac{3}{6} = frac{2+3}{6} = frac{5}{6}.
Сложение смешанных дробей
Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.
Пример решения задачи
Задание
Вычислить сумму дробей 2122frac{1}{2} и 3133frac{1}{3}.
Решение
В данном случае складываем отдельно целые и дробные части:
212+313=(2+3)+(12+13).2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}).
Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 6. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 3 и 2:
212+313=(2+3)+(12+13)=2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}) =
=5+(36+26)=5+56=556.= 5 +(frac{3}{6} +frac{2}{6}) = 5+frac{5}{6} = 5 frac{5}{6}.
На нашем сайте вы можете заказать задачу по алгебре недорого от опытных исполнителей!
Тест по теме «Сложение дробей»
Сложение дробей
Сложение дробей с одинаковыми знаменателями:
Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.
Формула
Сложим две дроби с одинаковым с одинаковыми знаменателями
По формуле складываем числители, а знаменатель оставляем исходный
Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.
Пример: 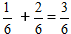
Сложение дробей с разными знаменателями:
Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.
Задача:
Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК – наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение:
2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21
Сложение дроби и целого числа:
Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.
Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.
Пример:
Решение:
Вычисляем целую часть, и получаем ответ
Сложение смешанных дробей:
Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.
Формула
Пример:
Подставляем цифры в формулу:
Получаем:
Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.
Сложение дробей с помощью онлайн калькулятора:
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Сложение и вычитание дробей с одинаковыми знаменателями
Ранее мы выполняли сложение и вычитание натуральных чисел. С дробными числами, или дробями, также можно выполнять данные действия.
Рассмотрим брусок:
Разделим его на 6 равных частей – долей:
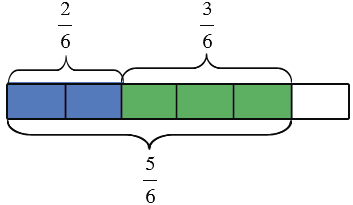
Закрасим две доли синим цветом и три – зеленым:
То есть получим, что две шестых закрашены синим, три шестых – зеленым, а всего закрашено пять шестых:
То есть мы можем сделать вывод, что:
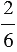
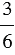
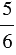
Опираясь на данный пример, можно сформулировать следующее правило:
Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Мы знаем, что вычитание натуральных чисел определяется на основе сложения: вычесть из одного числа другое – это значит найти такое число, которое при сложении с вычитаемым дает уменьшаемое. Аналогично вычитание дробей дается на основе их сложения.
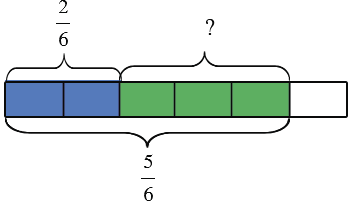
Например, рассмотрим наш брусок:
Нам известно, что на нем закрашено пять шестых частей, из которых две части синие, а остальные зеленые, нам надо найти какая часть бруска закрашена зеленым цветом:
Чтобы ответить на поставленный вопрос, нам надо найти разность дробей 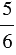
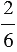
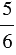
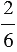
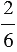
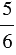
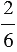
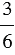
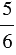
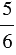
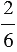
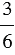
Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1014,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1019,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1042,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1099,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1251,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1369,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1731,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 743,
Мерзляк, Полонский, Якир, Учебник
Номер 1187,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 292,
Мерзляк, Полонский, Якир, Учебник
Номер 299,
Мерзляк, Полонский, Якир, Учебник
Номер 469,
Мерзляк, Полонский, Якир, Учебник
Номер 693,
Мерзляк, Полонский, Якир, Учебник
Номер 898,
Мерзляк, Полонский, Якир, Учебник
Номер 991,
Мерзляк, Полонский, Якир, Учебник
Номер 1006,
Мерзляк, Полонский, Якир, Учебник
Номер 1124,
Мерзляк, Полонский, Якир, Учебник
Задание 1081,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1226,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 5,
Мерзляк, Полонский, Якир, Учебник
Номер 74,
Мерзляк, Полонский, Якир, Учебник
Номер 113,
Мерзляк, Полонский, Якир, Учебник
Номер 114,
Мерзляк, Полонский, Якир, Учебник
Номер 255,
Мерзляк, Полонский, Якир, Учебник
Номер 348,
Мерзляк, Полонский, Якир, Учебник
Номер 386,
Мерзляк, Полонский, Якир, Учебник
Номер 481,
Мерзляк, Полонский, Якир, Учебник
Номер 646,
Мерзляк, Полонский, Якир, Учебник
Номер 1040,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 66,
Мерзляк, Полонский, Якир, Учебник
Номер 113,
Мерзляк, Полонский, Якир, Учебник
Номер 135,
Мерзляк, Полонский, Якир, Учебник
Номер 185,
Мерзляк, Полонский, Якир, Учебник
Номер 214,
Мерзляк, Полонский, Якир, Учебник
Номер 242,
Мерзляк, Полонский, Якир, Учебник
Номер 243,
Мерзляк, Полонский, Якир, Учебник
Номер 251,
Мерзляк, Полонский, Якир, Учебник
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 255,
Мерзляк, Полонский, Якир, Учебник
Содержание:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
- Сложение смешанных дробей
Сложение дробей с одинаковыми знаменателями
Определение
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме
числителей исходных дробей, а знаменатель – знаменателю дробей, то есть
$frac{a}{b}+frac{c}{b}=frac{a+c}{b}$
Чтобы сложить две дроби с одинаковым знаменателем, надо сложить
их числители и результат записать в числитель, а
знаменатель оставить без изменения.
Пример
Задание. Найти сумму дробей
$frac{3}{11}$ и
$frac{7}{11}$
Решение. $frac{3}{11}+frac{7}{11}=frac{3+7}{11}=frac{10}{11}$
Ответ. $frac{3}{11}+frac{7}{11}=frac{10}{11}$
Если в результате сложения получается дробь, числитель и знаменатель которой можно сократить,
то для конечного результата выполняем и сокращение дроби.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму дробей
$frac{3}{14}$ и
$frac{11}{14}$
Решение. Складываются дроби с одинаковым знаменателем,
поэтому просто складываем числитель, а знаменатель оставляем исходный:
$frac{3}{14}+frac{11}{14}=frac{14}{14}$
Полученная дробь $frac{14}{14}$ является
неправильной, у которой числитель равен знаменателю, и такая дробь равна единице, то есть
$frac{3}{14}+frac{11}{14}=frac{14}{14}=1$
Ответ. $frac{3}{14}+frac{11}{14}=1$
Сложение дробей с разными знаменателями
Определение
Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а
далее складывать как дроби с общим знаменателем.
Пример
Задание. Сложить дроби
$frac{2}{3}$ и
$frac{1}{8}$
Решение. Так как дроби с разными знаменателями, то вначале приведем их к
наименьшему общему знаменателю. Для этого найдем НОК чисел 3 и 8:
НОК (3, 8) = 24
Дополнительные множители к каждой из дробей соответственно:
$24 : 3=8,24 : 8=3$
то есть
$frac{2}{3}+frac{1}{8}=frac{2^{8}}{3}+frac{1^{3}}{8}=frac{2 cdot 8+1 cdot 3}{24}=frac{16+3}{24}=frac{19}{24}$
Ответ. $frac{2}{3}+frac{1}{8}=frac{19}{24}$
Замечание. После первого знака равенства справа вверху у каждой дроби указан дополнительный множитель к ней.
Сложение смешанных дробей
Определение
Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.
Пример
Задание. Вычислить сумму дробей
3$frac{2}{5}$ и
4$frac{7}{10}$
Решение. В данном случае складываем отдельно целые и дробные части:
$3 frac{2}{5}+4 frac{7}{10}=(3+4)+left(frac{2}{5}+frac{7}{10}right)$
Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 10, так как НОК
знаменателей 5 и 10. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 2 и 1:
$3 frac{2}{5}+4 frac{7}{10}=7+frac{2^{2}}{5}+frac{7^{1}}{10}=7+frac{2 cdot 2+7 cdot 1}{10}=7+frac{11}{10}=7 frac{11}{10}$
Так как дробная часть представляет собой
неправильную дробь, то выделяем целую часть:
$3 frac{2}{5}+4 frac{7}{10}=7 frac{11}{10}=7left(1+frac{1}{10}right)=8 frac{1}{10}$
Ответ. $3 frac{2}{5}+4 frac{7}{10}=8 frac{1}{10}$
Читать следующую тему: вычитание дробей.