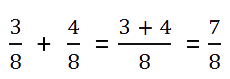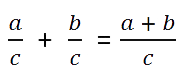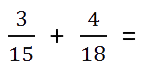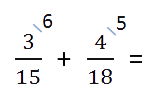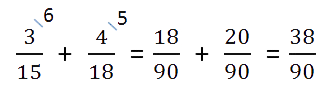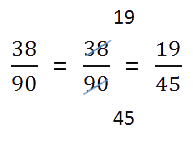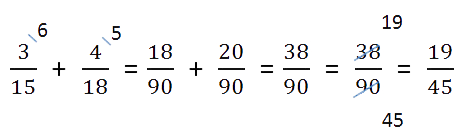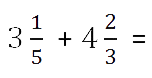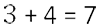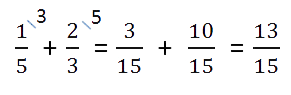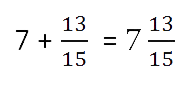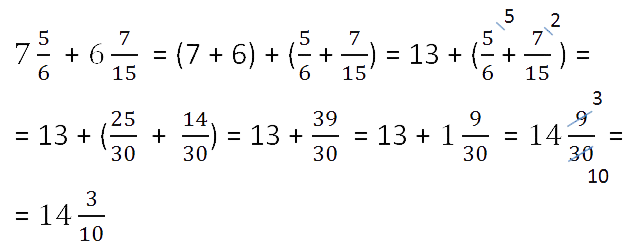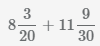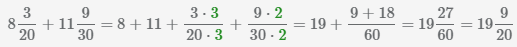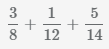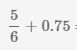Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Сложение дробей
Поддержать сайт
При сложении дробей могут встретиться разные случаи.
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают
числители, а знаменатель оставляют тот же.
Пример.
C помощью букв это правило сложения можно записать так:
Запомните!
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться
следующими правилами.
- Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти
наименьшее общее кратное знаменателей.
Пример. Сложить дроби.
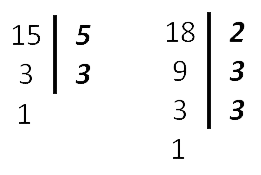
Как найти общий знаменатель
Находим НОК (15, 18).
НОК (15, 18) = 3 · 2 · 3 · 5 = 90
- Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1)
делим по очереди на знаменатель каждой дроби.Полученные числа и будут дополнительными множителями
для каждой из дробей. Множители записываем над числителем дроби справа сверху.90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
- Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь
основным свойством дроби.После умножения в знаменателях
обеих дробей должен получиться наименьший общий знаменатель.
Затем складываем дроби как дроби с одинаковыми знаменателями.
- Проверяем полученную дробь.
- Eсли в результате получилась
неправильная дробь,
результат записываем в виде смешанного числа. Проверим нашу
дробь.38 < 90
У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
- Eсли в результате получилась
- Ещё раз весь пример целиком.
Сложение смешанных чисел
Сочетательное и переместитительное свойства сложения позволяют привести
сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Чтобы сложить смешанные числа нужно.
- Отдельно сложить их целые части.
Пример.
Складываем целые части.
- Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то
сначала приводим их к общему знаменателю, а затем складываем. - Сложить полученные результаты из пунктов 1 и 2.
- Если при сложении дробных частей получилась неправильная дробь, то нужно
выделить целую часть из этой дроби и прибавить к полученной
в пункте 1 целой части.
Ещё один пример на сложение смешанных чисел.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
24 декабря 2018 в 11:19
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
2 января 2019 в 14:18
Ответ для Baur Nurgazinov
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
1) приводим все дроби к общему знаменателю
(2 -1 ) · х=
2) Вычислаем разность в скобках
( — ) · х=
· х=
сократим дроби на 3
· х=
3) вычисляем х
х= :
По правилу деления дробей делитель переворачиваем
x= · =
4 — сокращаем
х=3
Проверка:
(2 -1 ) · 3=( – ) · 3= · 3= · 3 = · = =
Ответ верный
0
Спасибо
Ответить
24 января 2017 в 19:44
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
24 января 2017 в 21:12
Ответ для Фанис Газизов
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
?
0
Спасибо
Ответить
1 марта 2016 в 18:39
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
спасибо сайт класс тему не понял
| было очень непонятно |
| теперь понятно + + |
+ + + + · + + + + +
0
Спасибо
Ответить
19 сентября 2016 в 13:05
Ответ для Денис Демидов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
6 февраля 2016 в 18:54
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Сложи
числа 30 и
числа 14.
0
Спасибо
Ответить
10 февраля 2016 в 19:03
Ответ для Денис Бочин
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
1) от 30=;
2)
от 14=
2)
+ ===24=24
0
Спасибо
Ответить
14 января 2016 в 15:31
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
2/6 или1/2 сравнение дробей
0
Спасибо
Ответить
14 января 2016 в 18:05
Ответ для Анжела Волк
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
больше
0
Спасибо
Ответить
19 сентября 2016 в 10:33
Ответ для Анжела Волк
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Отрицательное число всегда меньше положительного =)
0
Спасибо
Ответить
27 декабря 2015 в 20:00
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
19 сентября 2016 в 10:07
Ответ для Надежда Егина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
· a12· b4 · · a8· b5 = · a20 · b9=125· a20 · b9При раскрытии скобок отбросил знак ?, т.к. степень чётная, а значит получится +.
0
Спасибо
Ответить
21 апреля 2015 в 15:17
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
1) 15 — 7
4/7= 2) 20
4/5 — 1
5/6 *
1/3
3) 5
1/3 + 4
1/3 +
2/5
0
Спасибо
Ответить
14 апреля 2016 в 12:32
Ответ для Алина Гимадеева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Судя по всему, не разобрались с использованием кнопки дробь. Интерпретирую задачу следующим образом:
1) 15 ? 7
=8
2) 20
? 1 · = ? = = = =9 — похоже ошибка в примере, он гораздо сложнее двух других.
3) 5
+4 + = 9 + = + = = =10
0
Спасибо
Ответить
7 апреля 2015 в 20:06
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
как решить?4
+
0
Спасибо
Ответить
7 апреля 2015 в 21:13
Ответ для Александр Гридюшко
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
4+ = + = + = = = = 6
0
Спасибо
Ответить
14 апреля 2015 в 16:55
Ответ для Александр Гридюшко
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
4 + = + = = =16:3=1
0
Спасибо
Ответить
16 апреля 2015 в 19:06
Ответ для Александр Гридюшко
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Asel не правильно
0
Спасибо
Ответить
Чтобы сложить смешанные числа, надо записать их в виде неправильных дробей, а затем сложить как обыкновенные дроби.
Часто удобней вначале сложить целые части, а затем дробные части, избегаю преобразования в неправильную дробь.
Пример Сложить смешанные числа 
Сократим дробь 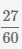
и деления полученного числа на числитель и знаменатель, НОД(27,60)=3,
получим 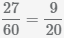
Пример Найти сумму смешанных чисел 
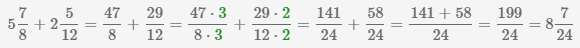
В результате сложения также получим смешанное число.
Сложение нескольких дробей
Пример Сложить 3 дроби 
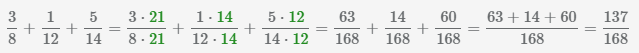
Сложение обыкновенных и десятичных дробей
Пример Найти сумму 
Для сложения десятичных и обыкновенных дробей нужно преобразовать их к одному формату. В данном примере преобразуем десятичную дробь
0.75 в обыкновенную дробь 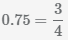

Математика
5 класс
Урок № 56
Сложение дробей с разными знаменателями
Перечень рассматриваемых вопросов:
– сумма дробей с разными знаменателями;
– моделирование сложения дробей с помощью реальных объектов, рисунков и схем.
Тезаурус
Сумма дробей с общим знаменателем – это дробь, числитель которой равен сумме числителей, а знаменатель равен знаменателю данных дробей.
Наименьший общий знаменатель (НОЗ) – это минимальное число, которое делится на знаменатели всех дробей выражения.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Сумма дробей с общим знаменателем – это дробь, числитель которой равен сумме числителей, а знаменатель равен знаменателю данных дробей.
Соответственно, чтобы выразить одну четверть часа в минутах, нужно привести дробь к знаменателю шестьдесят, то есть и числитель, и знаменатель умножить на пятнадцать.
Значит, общее расстояние, которое проехала Аня:
560 м + 450 м = 1010 м
Ответ: 1010 м
В задачах мы приводили все числа к одним единицам измерения, то есть складывали однородное. Это правило справедливо и для дробей с разными знаменателями.
Чтобы сложить две дроби с разными знаменателями, их надо привести к общему знаменателю, а затем применить правило сложения дробей с общим знаменателем.
Но казалось бы тема всем или многим знакомая, а некоторым, и не очень интересная. А вот бывает, что и самим приходится складывать такие дроби, или своим детям объяснять. А вот это святое – объяснить своему сыну или внучке, учащимся с 4 по 7 (даже) классы, эту тему. И если это тема в своё время как-то не зацепилась в голове, то сейчас самое время, чуть обратить на этот момент внимание.
Для рассмотрения будем брать дроби, знаменатели которых не имеют общих множителей. Пусть нужно сложить такие дроби:
3/7 + 5/9 = ?
Пояснение к быстрой методике дам на рисунке и в статье.
В числителе сумма произведений цифр по красной стрелке и по зелёной стрелке, а в знаменателе – произведение знаменателей обоих дробей.
Считаем: (3*9 + 5*7)/7*9 = (27 + 35)/63 = 62/63.
Как и предполагалось получились числа, которые нельзя сократить. Если некратные знаменатели, то и в сумме дробей получим несократимую дробь. И если в задании будет сумма дробей с различными знаменателями, причём, не кратными, то и дробь будет несократимая в результате. Поэтому выбрать верный ответ в таких суммах легко, Пройдите тест по закреплению материала.
Форма тесты : сложение дробей.
Что хочу подчеркнуть, выбрать сумму дробей, из трёх предложенных ответов не сложно, если знать, что в каждом приведённом примере, должна получиться несократимая дробь, потому что в сумме участвуют дроби, которые состоят из чисел, которые не имеют общих множителей. Поэтому и сумма не будет иметь общих множителей в числителе и в знаменателе. И выбрать это можно устно.
Так, например, в примере 1. из трёх ответов 43/55, 45/55, 40/55, две из дробей несократимые, а 43/55, дробь несократимая, и это ответ. Понятно? Если не очень понятно, то пишите в комментариях, и будем объяснять.
Вариант 2. 31/20 – несократимая дробь.
Вариант 3. 63/80 – несократимая дробь, ответ.
Вот на этой основе и решаются такие примеры устно. Можно решать и по-другому, письменно, с карандашиком, и решать. По рисунку, приведённому вверху легко понять:
Сумма произведений чисел по красной стрелке плюс произведение средних чисел по зелёной стрелке делится на произведение знаменателей дробей. Всё просто по рисунку, или сами накидайте рисунок. Дроби это не сложно.
Спасибо за прочтение. И подписывайтесь на канал. Делитесь статьёй в соцсетях.
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель – знаменателю дробей, то есть ab+cb=a+bcfrac{a}{b} + frac{c}{b} = frac{a+b}{c}.
Сложение дробей с одинаковыми знаменателями
Чтобы сложить две дроби с одинаковым знаменателем, надо сложить их числители и результат записать в числитель, а знаменатель оставить без изменения.
Примеры решения задач
Задание
Найти сумму дробей 513frac{5}{13} и 113.frac{1}{13}.
Решение
513+113=613frac{5}{13} + frac{1}{13} = frac{6}{13}
Задание
Найти сумму дробей 512frac{5}{12} и 112frac{1}{12}.
Решение
Складываются дроби с одинаковым знаменателем, поэтому просто складываем числитель, а знаменатель оставляем исходный:
512+112=612frac{5}{12} + frac{1}{12} = frac{6}{12}.
Полученную можно упростить – путем сокращения числителя и знаменателя на 6, то есть 512+112=612=12frac{5}{12} + frac{1}{12} = frac{6}{12} = frac {1}{2}.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а далее складывать как дроби с общим знаменателем.
Пример решения задачи
Задание
Сложить дроби 13frac{1}{3} и 12frac{1}{2}.
Решение
Так как дроби с разными знаменателями, то вначале приведем их к наименьшему общему знаменателю. Для этого найдем НОК чисел 2 и 3:
НОК (3, 2) = 6
Дополнительные множители к каждой из дробей соответственно: 6:3=2, 6:2=3, то есть
13+12=26+36=2+36=56.frac{1}{3} + frac{1}{2} = frac{2}{6} + frac{3}{6} = frac{2+3}{6} = frac{5}{6}.
Сложение смешанных дробей
Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.
Пример решения задачи
Задание
Вычислить сумму дробей 2122frac{1}{2} и 3133frac{1}{3}.
Решение
В данном случае складываем отдельно целые и дробные части:
212+313=(2+3)+(12+13).2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}).
Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 6. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 3 и 2:
212+313=(2+3)+(12+13)=2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}) =
=5+(36+26)=5+56=556.= 5 +(frac{3}{6} +frac{2}{6}) = 5+frac{5}{6} = 5 frac{5}{6}.
На нашем сайте вы можете заказать задачу по алгебре недорого от опытных исполнителей!