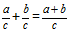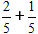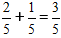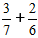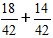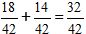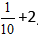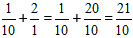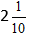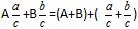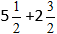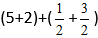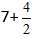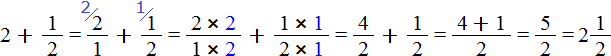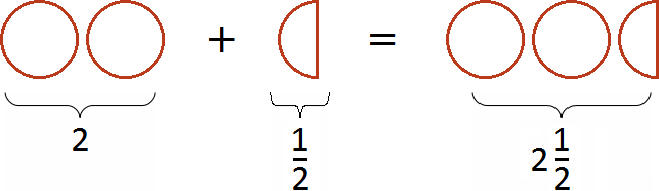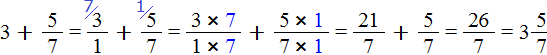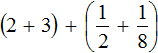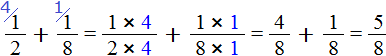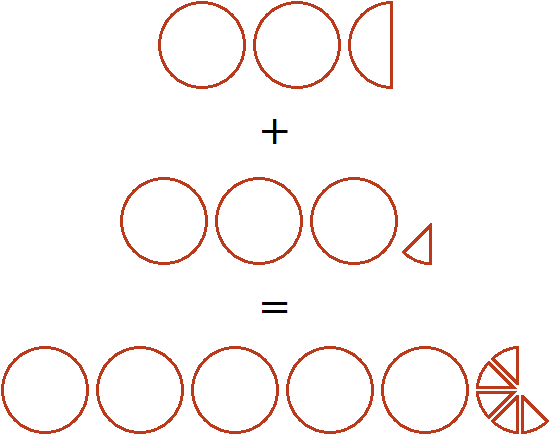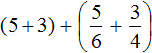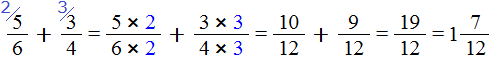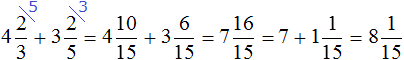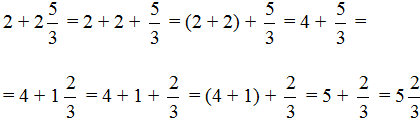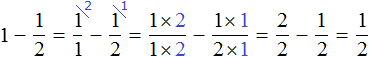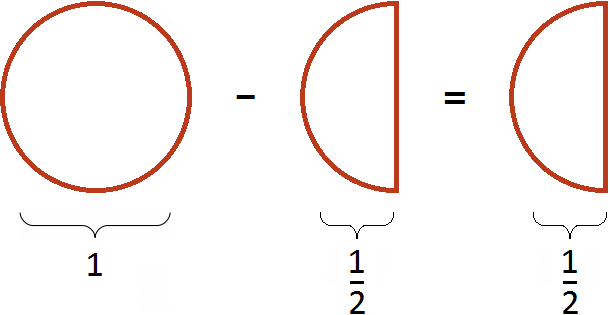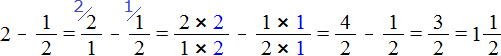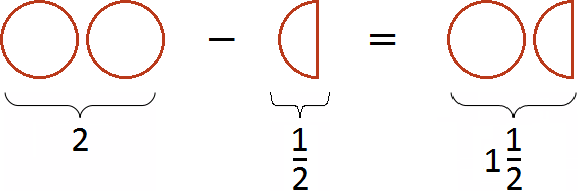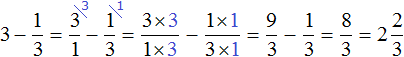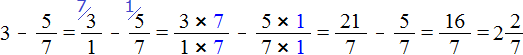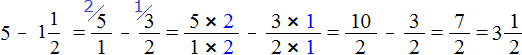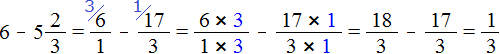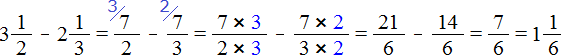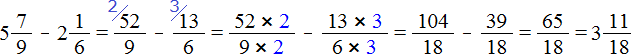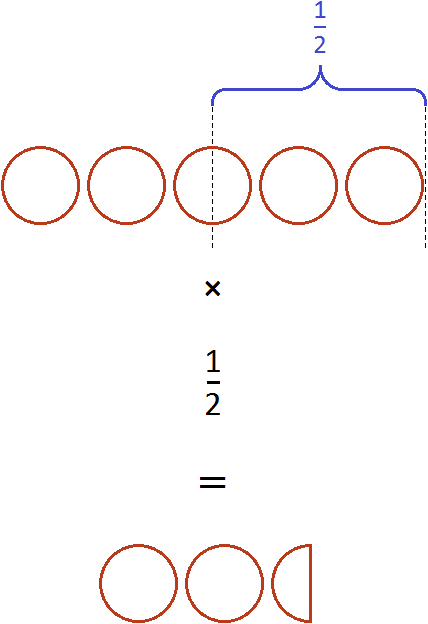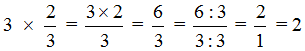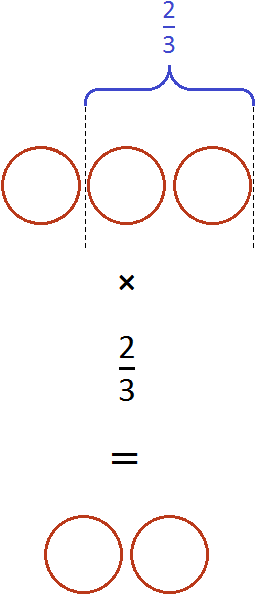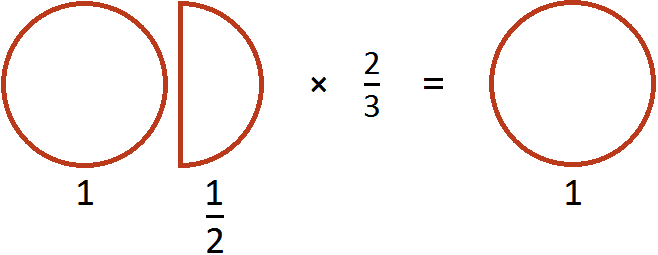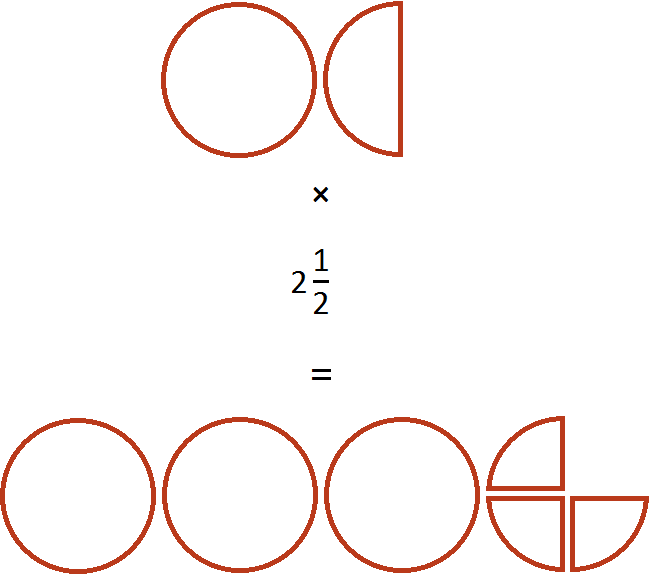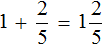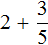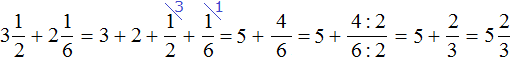Как найти сумму дроби с целым числом

Как найти сумму дроби с целым числом

Сложение дробей

Сложение дробей с одинаковыми знаменателями:

Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.

Формула

Сложим две дроби с одинаковым с одинаковыми знаменателями

По формуле складываем числители, а знаменатель оставляем исходный

Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.

Пример: 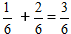При сокращении дроби у нас получится число 1/2

Сложение дробей с разными знаменателями:

Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.
Задача:

Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК – наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение:

2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21

Сложение дроби и целого числа:

Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.

Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.

Пример:

Решение:
Вычисляем целую часть, и получаем ответ

Сложение смешанных дробей:

Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.
Формула
Пример:
Подставляем цифры в формулу:
Получаем:

Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.

Сложение дробей с помощью онлайн калькулятора:

×

Пожалуйста напишите с чем связна такая низкая оценка:

×

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.

Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.

Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.

Сложение целого числа и правильной дроби

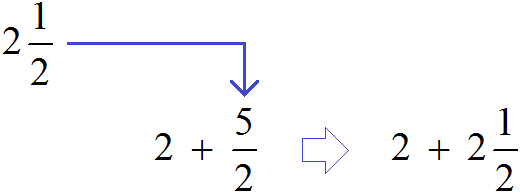
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь одна вторая. Чтобы решить этот пример, нужно число 2 представить в виде дроби две первых . Затем сложить дроби с разными знаменателями:

два прибавить одну вторую будет две целых одна вторая

А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: два плюс одна вторая, а конец так: две целых одна вторая. Различие в том, что в первом случае число 2 и дробь одна вторая соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что две целых одна вторая это свёрнутая форма записи смешанного числа, а два плюс одна вторая — развёрнутая.

Когда перед нами смешанное число вида две целых одна вторая , мы должны понимать, что знак сложения опущен.

Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.

Значит значение выражения два плюс одна вторая равно две целых одна вторая

два плюс одна вторая будет две целых и одна вторая

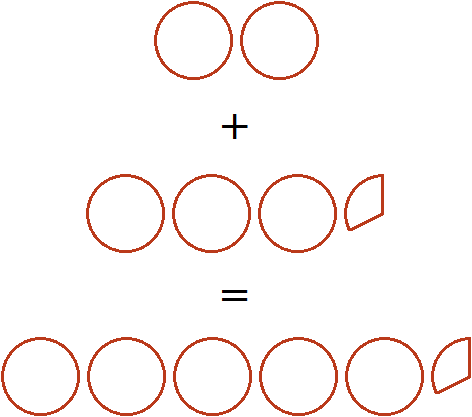
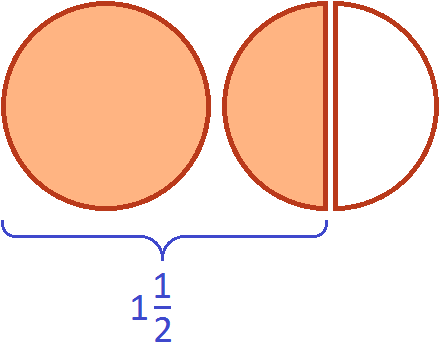
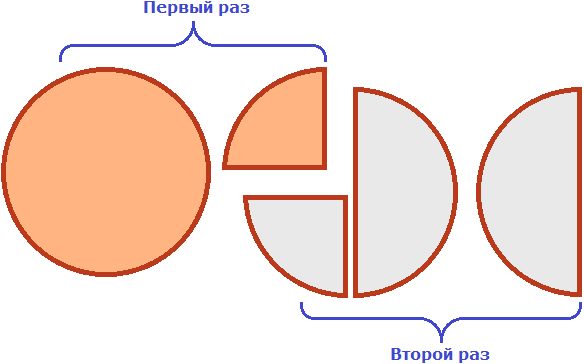
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:

две целых плюс половина решение в пиццах

Пример 2. Найти значение выражения 152

Представим число 3 в виде дроби 1522. Затем сложим дроби с разными знаменателями:

1523

Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:

1526

Пример 3. Найти значение выражения две плюс две пятых

Можно записать вместе число 2 и дробь пять вторых, но этот ответ не будет окончательным, поскольку в дроби пять вторых можно выделить целую часть.

Поэтому в данном примере сначала нужно выделить целую часть в дроби пять вторых . Пять вторых это две целых и одна вторая:

выделение целой части в дроби пять вторых

Теперь в главном выражении две плюс две пятых вместо дроби пять вторых запишем смешанное число две целых одна вторая

две плюс две пятых шаг 2

Получили новое выражение два плюс две целых одна вторая. В этом выражении смешанное число две целых одна вторая запишем в развёрнутом виде:

два плюс два плюс одна вторая

Применим сочетательный закон сложения. Сложим две двойки, получим 4:

четыре плюс половина

Теперь свернём полученное смешанное число:

четыре плюс половина сворачивание

Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:

две плюс две пятых окончательное решение

Сложение смешанных чисел

Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения 1531. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.

Для начала запишем смешанные числа в развёрнутом виде:

1532

Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:

2 plus 3 plus 1 na 2 plus 1 na 8

Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:

5 plus 1 na 2 plus 1 na 8

Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:

1535

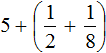
Получили  1536 . Теперь в главном выражении 5 plus 1 na 2 plus 1 na 8 заменяем дробные части на полученную дробь 1536

1537

Теперь свернем полученное смешанное число:

1538

Таким образом, значение выражения 1531 равно 1539. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:

5 plus 1 na 2 plus 1 na 8 pic

Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:

15310

Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.

Пример 2. Найти значение выражения 5 на 5 на 6 плюс 3 на 3 на 4 пример

Запишем смешанные числа в развёрнутом виде:

5 на 5 на 6 плюс 3 на 3 на 4 рисунок 1

Сгруппируем целые и дробные части по отдельности:

5 на 5 на 6 плюс 3 на 3 на 4 рисунок 2

Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8

5 на 5 на 6 плюс 3 на 3 на 4 рисунок 3

Теперь вычислим дробные части:

1544

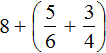
Получили смешанное число 1545. Теперь в главном выражении 5 на 5 на 6 плюс 3 на 3 на 4 рисунок 3 заменяем выражение в скобках на полученное смешанное число 1545

5 на 5 на 6 плюс 3 на 3 на 4 рисунок 4

Получили выражение 5 на 5 на 6 плюс 3 на 3 на 4 рисунок 4. В данном случае число 8 надо прибавить к целой части смешанного числа 1545 . Для этого смешанное число 1545 можно временно развернуть, чтобы было понятнее, что с чем складывать:

1547

Сложим целые части. Получаем 9

1549

Сворачиваем готовый ответ:

1550

Таким образом, значение выражения 5 на 5 на 6 плюс 3 на 3 на 4 пример равно 1551.

Полное решение этого примера выглядит следующим образом:

1552

Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:

Чтобы сложить смешанные числа, надо:

  • привести дробные части этих чисел к общему знаменателю;
  • отдельно выполнить сложение целых и дробных частей.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.

Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.

Пример 3. Найти значение выражения 4 na 2 na 3 plus 3 na 2 na 5

Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:

4 na 2 na 3 plus 3 na 2 na 5 step 2

Сложение целого и смешанного числа

Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число 1561 . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:

1562

Здесь смешанная дробь 1561 была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ 1563.

Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:

2 plus 3 na 1 na 3 pic

Пример 2. Найти значение выражения 1564

В этом примере, как и в предыдущем, нужно сложить целые части:

1573

Осталось свернуть целую и дробную части, но дело в том, что дробная часть 1574  представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:

1575

Вычитание дроби из целого числа

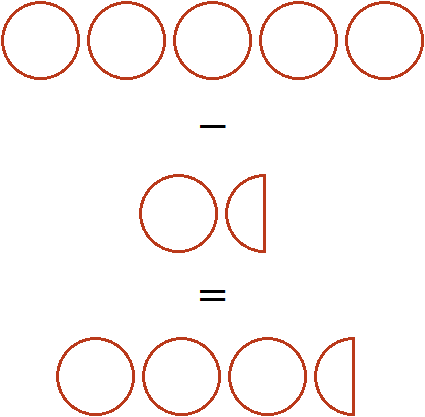
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь одна вторая. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби 1na1 , и выполнить вычитание дробей с разными знаменателями:

1 na 1 minus 1 na 2 ravno 1 na 2 step 1

Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:

1 na 1 minus 1 na 2 ravno 1 na 2 step 2

Пример 2. Найти значение выражения 1581.

Представим число 2 в виде дроби 14167 , и выполним вычитание дробей с разными знаменателями:

1582

Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:

2 minus 1 na 2 рисунок 1

Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения 3 минус 1 на 3, не приводя на бумаге никаких вычислений.

Представим, что число 3 это три пиццы:

3 na 1 na 2 рисунок 1

Нужно вычесть из них одна третья. Мы помним, что треть выглядит следующим образом:

3 минус 1 на 3 рисунок 2

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

3 минус 1 на 3 рисунок 3

Получилось две целых две третьих (две целых и две трети пиццы).

Чтобы убедиться в правильности решения, можно найти значение выражения 3 минус 1 на 3 обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:

3 минус 1 на 3 решение

Пример 3. Найти значение выражения 1591

Представим число 3 в виде дроби 1592. Затем выполним вычитание дробей с разными знаменателями:

1593

Вычитание смешанного числа из целого числа

Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения пять минус одна целая и одна вторая .

Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число одна целая и одна вторая перевести в неправильную дробь. После перевода смешанного числа одна целая и одна вторая в неправильную дробь, получим дробь 15123. Теперь выполним вычитание дробей с разными знаменателями:

15124

Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:

5-1 na 1 na 2 рисунок

Пример 2. Найти значение выражения 15131

Представим 6 в виде дроби 15132 , а смешанное число 15133, в виде неправильной дроби. После перевода смешанного числа 15133  в неправильную дробь, получим дробь 15134. Теперь выполним вычитание дробей с разными знаменателями:

15135

Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.

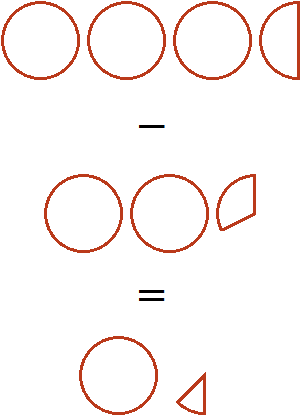
К примеру, если нужно быстро найти значение выражения 2 minus 2 na 3 step 1, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

2 minus 2 na 3 step 3

Тогда от той пиццы, от которой отрезали две третьих останется одна третья пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:

2 minus 2 na 3 step 2

Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.

Вычитание смешанных чисел

Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения: 15141

Чтобы решить этот пример, нужно смешанные числа 15142 и 15143 перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:

15144

Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:

3 na 1 na minus 2 na 1 na 3 рисунок

Пример 2. Найти значение выражения 15141

Переводим смешанные числа 15142 и 15143 в неправильные дроби и выполняем вычитание дробей с разными знаменателями:

15144

К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.

А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.

Умножение целого числа на дробь

Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.

Например, умножим число 5 на дробь одна вторая. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби одна вторая, а знаменатель оставить без изменения:

15151

В ответе получилась неправильная дробь. Выделим в ней целую часть:

15152

Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:

5 na 1 na 2 рисунок

Пример 2. Найти значение выражения 15161

Умножим число 3 на числитель дроби 15163

15162

В ответе получилась неправильная дробь 15164, но мы выделили её целую часть и получили 2.

Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:

15165

Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:

3 na 2 na 3 рисунок

Пример 3. Найти значение выражения 15171

Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:

15172

Пример 4. Найти значение выражения 15181

Умножим число 3 на числитель дроби одна вторая

15183

Умножение смешанного числа на дробь

Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.

Пример 1. Найти значение выражения 2 na 1 na 2 na 2 na 3 ravno 1

Переведём смешанное число  в неправильную дробь. После перевода это число превратится в дробь три вторых. Затем можно будет умножить эту дробь на две третьих

2 na 1 na 2 na 2 na 3 ravno 1 решение

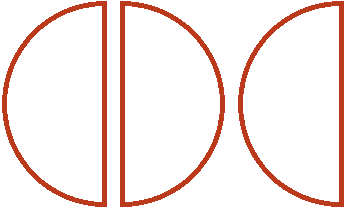
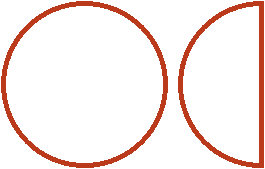
Допустим, имеются одна целая и половина пиццы:

2 na 1 na 2 na 2 na 3 ravno 1 рисунок 1

Умножить эти куски на две третьих означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:

2 na 1 na 2 na 2 na 3 ravno 1 рисунок 2

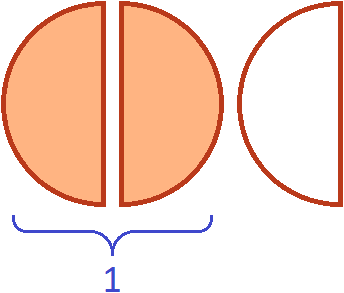
Теперь если мы возьмем две третьих (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:

2 na 1 na 2 na 2 na 3 ravno 1 рисунок 3

Поэтому значение выражения 2 na 1 na 2 na 2 na 3 ravno 1 было равно 1

2 na 1 na 2 na 2 na 3 ravno 1 рисунок 4

Умножение смешанных чисел

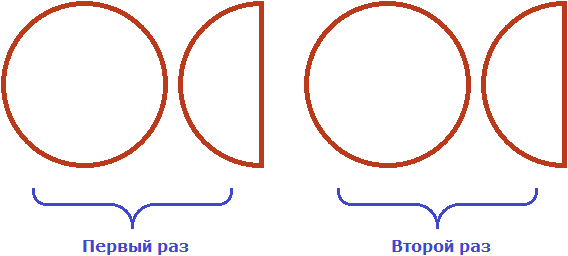
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить  и две целых одна вторая. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:

1 na 1 na 2 na 2 na 1 na 2 решение

Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:

1 na 1 na 2 na 2 na 1 na 2 рисунок 1

Теперь разберемся со смешанным множителем две целых одна вторая. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще одна вторая раза.

С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:

1 na 1 na 2 na 2 na 1 na 2 рисунок 2

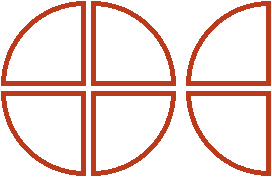
Но ещё осталось взять одна вторая от изначальной целой пиццы и половины, ведь множителем было смешанное число две целых одна вторая. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:

1 na 1 na 2 na 2 na 1 na 2 рисунок 3

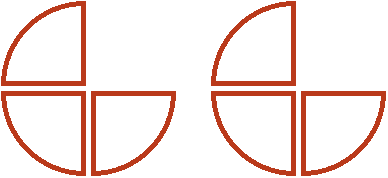
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является три четвёртых пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:

1 na 1 na 2 na 2 na 1 na 2 рисунок 4

А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является три четвёртыхпиццы.

Поэтому значение выражения 1 na 1 na 2 na 2 na 1 na 2 равно 3 na 3 na 4

1 na 1 na 2 na 2 na 1 na 2 рисунок 5

Пример 2. Найти значение выражения 2 на 1 на 3 на 3 на 1 на 4 пример

Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:

2 на 1 на 3 на 3 на 1 на 4 решение

Деление целого числа на дробь

Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.

Например, разделим число 3 на дробь одна вторая. Здесь число 3 — это делимое, а дробь одна вторая — делитель.

Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби одна вторая. А обратная дробь для дроби одна вторая это дробь две первых. Поэтому умножаем число 3 на дробь 15221

3 na 1 na 2 решение

Допустим, имеются три целые пиццы:

3 na 1 na 2 рисунок 1

Если мы зададим вопрос «cколько раз одна вторая (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».

Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:

3 na 1 na 2 рисунок 2

Поэтому значение выражения 3 na 1 na 2 выражение равно 6.

Пример 2. Найти значение выражения 2 на 3 на 2 пример

Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби три вторых. А обратная дробь для дроби три вторых это дробь две третьих

2 на 3 на 2 решение

Допустим, имеются две целые пиццы:

2 на 3 на 2 рисунок 1

Зададим вопрос «Сколько раз три вторых пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби три вторых. После выделения целой части в этой дроби получим 

Теперь поставим вопрос так: «Сколько раз  (одна целая и половина пиццы) содержится в двух пиццах?».

Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

2 на 3 на 2 рисунок 5

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

2 на 3 на 2 рисунок 2

А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

2 на 3 на 2 рисунок 4

Поэтому значение выражения 2 на 3 на 2 пример равно одна целая одна третья

Пример 3. Найти значение выражения 5 na 9 na 2

Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби 9 na 4. А обратная дробь для дроби 9 na 4 это дробь 4 na 9. Поэтому умножаем число 5 на 4 na 9

5 na 9 na 4 решение

Дробь 9 na 4 это 2 целых и одна четвертая. Проще говоря, две целые и четверть пиццы:

5 na 9 na 4 рисунок 1

А выражение 5 na 9 na 2 определяет сколько раз  содержится в пяти целых пиццах. Ответом было смешанное число 2 na 2 na 9.

То есть  пиццы содержится в пяти целых пиццах 2 na 2 na 9 раза.

Давайте нащупаем в пяти пиццах два раза по 

5-1 na 1 na 2 рисунок 3

Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой две девятых от , которые не вместились. Двумя девятыми они являются по той причине, что в  пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:

5-1 na 1 na 2 рисунок 4

Поэтому значение выражения 5 na 9 na 2 равно 2 na 2 na 9

Деление дроби на целое число

Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.

Пример 1. Разделим дробь одна вторая на число 2

Чтобы разделить дробь одна вторая на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь одна вторая

1 на 2 на 2 решение

Пусть имеется половина пиццы:

рисунок половина пиццы

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:

1 na 2 na 2 рисунок

Поэтому значение выражения 1 na 2 na 2 равно одна четвертая

Пример 2. Найти значение выражения 5 на 7 на 2 пример

Чтобы решить этот пример, нужно дробь 5 на 7 умножить на число, обратное числу 2. Обратное числу 2 это дробь одна вторая

5 на 7 на 2 решение

Пример 3. Найти значение выражения 3 на 5 на 3 пример

Умножаем первую дробь Три пятых на число, обратное числу 3. Обратное числу 3 это дробь одна третья

3 на 5 на 3 решение

Деление целого числа на смешанное число

Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .

Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.

Переведём делитель  в неправильную дробь, получим три вторых. Затем умножим 2 на дробь, обратную дроби три вторых. Обратная для дроби три вторых это дробь две третьих

2 на 1 на 1 на 2 решение

Допустим, имеются две целые пиццы:

2 на 3 на 2 рисунок 1

Зададим вопрос «Сколько раз  (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

2 на 3 на 2 рисунок 2

А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

2 на 3 на 2 рисунок 4

Поэтому значение выражения 2 на 1 на 1 на 2 пример равно одна целая одна третья

Пример 2. Найти значение выражения 5 на 2 на 1 на 7 пример

Переводим делитель 2 на 1 на 7 в неправильную дробь, получаем 15 на 7. Теперь умножаем число 5 на дробь, обратную дроби 15 на 7. Обратная для дроби 15 на 7 это дробь 7 на 15

5 на 2 на 1 на 7 решение

Сначала мы получили ответ 152611, затем сократили эту дробь на 5, и получили 7 на 3, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ две целых одна третья

Деление смешанного числа на целое число

Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.

Например, разделим  на 2. Чтобы решить этот пример, нужно делимое  перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.

Переведём смешанное число  в неправильную дробь, получим три вторых.

Теперь умножаем три вторых на число, обратное числу 2. Обратное числу 2 это дробь одна вторая

1 на 1 на 2 на 2 решение

Допустим, имеется одна целая и половина пиццы:

1 на 1 на 2 на 2 рисунок 1

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

1 на 1 на 2 на 2 рисунок 2

Затем разделим поровну на две части и половину:

1 на 1 на 2 на 2 рисунок 3

Теперь если мы сгруппируем эти кусочки на две группы, то получим по три четвёртых пиццы в каждой группе:

1 на 1 на 2 на 2 рисунок 3

Поэтому значение выражения 1 на 1 на 2 на 2 пример равно три четвёртых

Пример 2. Найти значение выражения 3 на 1 на 5 на 4 пример

Переведём делимое 3 на 1 на 5 на 4 в неправильную дробь, получим 16 на 5. Теперь умножаем 16 на 5 на число, обратное числу 4. Обратное числу 4 это дробь 15294.

3 на 1 на 5 на 4 решение

Деление смешанных чисел

Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.

Пример 1. Найти значение выражения 2 на 1 на 2 на 1 на 1 на 4 шаг 1

Переведём смешанные числа в неправильные дроби. Получим следующее выражение:

2 на 1 на 2 на 1 на 1 на 4 шаг 2

Как решать дальше мы уже знаем. Первую дробь пять вторых нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь 4 на 5 .

Дорешаем данный пример до конца:

2 на 1 на 2 на 1 на 1 на 4 шаг 3

Допустим, имеются две целые и половина пиццы:

2 на 1 на 2 на 1 на 1 на 4 рисунок 1

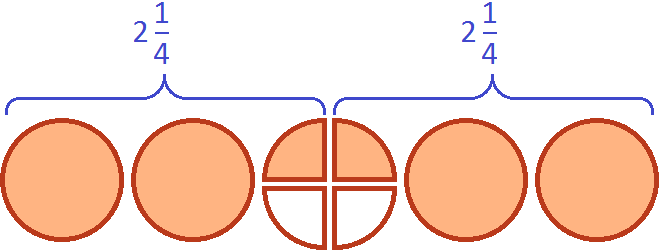
Если зададим вопрос «Сколько раз одна целая одна четвертая (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:

2 на 1 на 2 на 1 на 1 на 4 шаг 4

Пример 2. Найти значение выражения 15311

Переведём смешанные числа в неправильные дроби. Получим следующее выражение:

15312

Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь 15314

15316

Сначала мы получили дробь15317. Эту дробь мы сократили на 9. В результате получили дробь 15318, но такой ответ нас тоже не устроил и мы выделили в дроби 15318 целую часть. В результате получили окончательный ответ 15319.

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

Решение:

Задание 2. Найдите значение выражения:

Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже


Источник


Download Article


Download Article

Performing operations on different types of numbers can be a difficult task at times. Do you often forget the method? Don’t worry, in this article, wikiHow explains how you can add fractions to whole numbers using a fairly simple and quick method that saves you time and procrastination.

Steps

  1. Image titled How to add fractions to whole numbers step 1.png

    1

    Convert your whole number into a fraction. To do this, simply add a denominator of 1to your whole number.

  2. Image titled How to add fractions to whole numbers step 2.png

    2

    Multiply your fractions to have the same denominator. Look at the original fraction in your problem, and use its denominator to multiply with your other fraction.

    Advertisement

  3. Image titled How to add fractions to whole numbers step 3.png

    3

    Add both fractions. Now that you’ve got two fractions of the same denominator, add both fractions’ numerators, leaving the denominator as it is.

  4. Image titled How to add fractions to whole numbers step 4.png

    4

    Simplify your fraction. Convert your improper fraction to a mixed fraction. Doing this can get you either a mixed fraction, or a whole number. both would be correct depending on the numerator and denominator divisibility.

    5. Advertisement

Add New Question

  • Question

    Do you have to turn it into a mixed number?

    Community Answer

    No, the answer is correct without turning it into a mixed number. It’s just that mixed numbers are often more easily grasped than the equivalent improper fractions.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

  • If you have difficulty with your multiplication tables, using a calculator for the necessary parts can be okay as long as you have permission from your teacher.

Thanks for submitting a tip for review!

Advertisement

About This Article

Thanks to all authors for creating a page that has been read 33,432 times.

Did this article help you?

Источник

Как сложить смешанную и целое

Как сложить смешанную и целое, рассмотрим процесс сложения смешанной дроби и целого числа, и также , как складывать смешанную дробь и целое число на калькуляторе!?

О сложении смешанной дроби и целого :

  1. Правило сложения смешанной дроби и целого числа.
  2. Как сложить смешанную и целое!?
  3. Сложить смешанную дробь и целое число на калькуляторе.

  1. Правило сложения смешанной дроби и целого числа.

    Для того, чтобы сложить смешанную дробь и целое число нужно к целому числу смешанной дроби прибавить целое число! И это все правило!

    Рассмотрим данное правило на примере :

    Пример : как сложить смешанную дробь и число

    Предположим, что нам требуется прибавить к смешанной дроби : одна целая, одна вторая 1|1/2 прибавить число 2.

    1|1/2 + 2

    Берем целое у смешанной дроби складываем с целым числом :

    1|1/2 + 2 = (1 + 2) + 1/2 = 3 + 1/2 = 3|1/2

    Результат сложения смешанной дроби и целого числа :

    1|1/2 + 2 = 3|1/2

  2. Как сложить смешанную и целое!?

    Вообще, данное сложение – сложить смешанную и целое – одно из самых простых в сложении дробей!

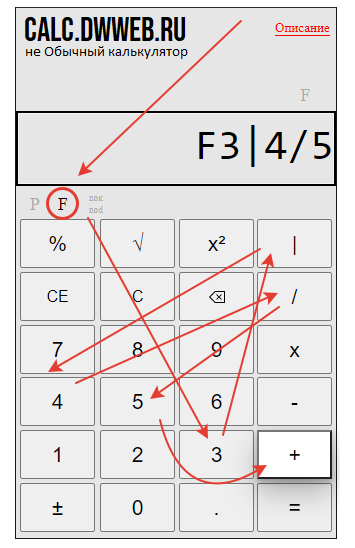
    Давайте рассмотрим, какой-то пример посложнее, пусть это будет 3|4/5 + 12 :

    3|4/5 + 12

    Поступаем с данным выражением аналогично выше приведенном правилу :

    Отделяем целы,

    3 + 4/5 + 12

    складываем целые :

    (3 + 12) + 4/5 = 15 + 4/5

    Возвращаем полученное целое к дроби :

    15 + 4/5 = 15|4/5

    Как проверить правильность вашего сложения смешанной и целого числа!?

    Для этого, сложим смешанную и целое число на калькуляторе

  3. Сложить смешанную дробь и целое число на калькуляторе.

    Не будем придумывать новые числа для сложения смешанной дроби и целого числа на калькуляторе., возьмем выге привелденный пример!
    3|4/5 + 12

    Набираем смешанную дробь на калькуляторе

    Нажимаем кнопку плюс – “+”.

    Сложить смешанную дробь и целое число на калькуляторе.

    Набираем целое число, которое будем прибавлять – 12.

    Нажимаем равно – “=”.

    Сложить смешанную дробь и целое число на калькуляторе.

    Получаем результат сложения смешанной дроби и целого числа :

    Сложить смешанную дробь и целое число на калькуляторе.

Не благодарите, но ссылкой можете поделиться!

COMMENTS+

 
BBcode

Источник

Что такое дробь в математике? 

Дробь – число, составленное из одной или нескольких равных долей единицы.

Это — само определение дроби. А более подробно ответ на вопрос «что такое дробь» (а также что такое «единица» в определении дроби) представлен ниже на конкретных примерах, а также в обучающем видео.

Пример 1.

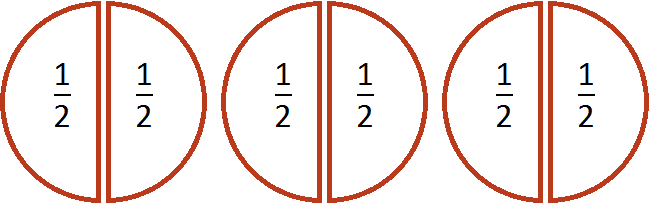
Круг разделили на две равные части, и одну из них взяли. Имеем дробь ½. Числитель дроби (1) показывает, сколько равных частей круга взяли (взяли одну часть). Знаменатель дроби показывает, на сколько равных частей разделили круг (делили его на две равные части).

Пример 2.

Круг разделили на три равные части. Взяли одну часть (т.е. 1/3). Взяли две части (т.е. 2/3).

Пример 3.

Торт разрезали на 8 равных кусков. Каждый кусок – это 1/8 торта. Папе в тарелку положили два куска (т.е. 2/8 торта), а бабушке – три куска (т.е. 3/8 торта).

Совершенно не обязательно «единица» в определении дроби на практике должна быть представлена кругом или тортом (как обычно её представляют в примерах из учебников) или чем-то монолитным физически.

Пример 4.

Бабушка купила 18 мотков пряжи. Себе она оставила 13 мотков (т.е. 13/18 покупки), а 5 мотков (т.е. 5/18 покупки) отдала внучке. В результате у внучки оказалось 5/13 того, что оставила себе бабушка. В данном примере сначала за единицу была принята вся покупка (18/18 = 1), а потом – то, что оставила себе бабушка (13/13 = 1).

Что такое смешанное число?

Смешанное число – число, в состав которого входит целое число и дробь. Например, 3½, 97/8. Читается это так: «три целых, одна вторая», «девять целых, семь восьмых» или «три целых и одна вторая», «девять целых и семь восьмых». Иногда слово «целых» пропускают и говорят так: «три и одна вторая», «девять и семь восьмых». Число 3½ можно представить, например, как три целых торта (обязательно одинаковых) и половину от четвертого такого же торта. Наглядно ответ на вопрос «что такое смешанное число» представлен в обучающем видео.  

Правильные и неправильные дроби

Числитель может быть меньше знаменателя, больше знаменателя или равен ему. В зависимости от этого различают дроби «правильные» и «неправильные». 

Правильная дробь – дробь, у которой числитель меньше знаменателя. Например, ½, 5/6, 9/10, 11/125, 144/145. 

Неправильная дробь – дробь, у которой числитель больше знаменателя или равен ему. Например, 3/2, 6/5, 10/9, 125/125, 145/144.

Как представить в своем воображении правильную дробь – описано в примерах выше. А неправильную дробь можно представить так (см. примеры ниже).

Пример.

На празднование дня рождения купили два одинаковых торта. Их оба порезали на одинаковое число кусков (на 8 кусков порезали первый торт и на столько же кусков порезали второй торт, всего получилось 8 + 8 = 16 одинаковых кусков). Но горячие блюда оказались настолько калорийными, что и первый торт был съеден не весь (5 кусков было съедено, а 3 куска остались на блюде), а второй торт (8 кусков) вообще остался нетронутым. Итого съедено было 5/8 одного торта, или 5/16 всего десерта. (5/8 и 5/16 – правильные дроби). А что осталось? Остался один целый торт (нарезанный на 8 кусков, т.е. 1 = 8/8) и ещё 3/8 такого же торта. Т.е. осталось 11/8 торта (одиннадцать восьмых, это неправильная дробь, т.к. числитель больше знаменателя).

Обращение неправильной дроби в смешанное число 

Чтобы обратить неправильную дробь в смешанное число, нужно числитель дроби разделить на знаменатель и найти остаток; частное покажет число целых единиц, а остаток – число долей единицы. 

Пример 1.

Нужно обратить неправильную дробь 25/4 в смешанное число.

Последовательность действий следующая.

1) Делить 25 на 4. Целых получается 6.

2) Умножить 6 (целых) на 4 (знаменатель), результат равен 24.

3) Вычесть 24 из 25 – и получается остаток 1.

В результате получено смешанное число 61/4 (шесть целых и одна четвертая).

Пример 2.

Нужно обратить неправильную дробь 106/14 в смешанное число.

Последовательность действий следующая.

1) Делить 106 на 14. Целых получается 7.

2) Умножить 7 (целых) на 14 (знаменатель), результат равен 98.

3) 106 – 98 = 8.

В результате получено смешанное число 78/14 (семь целых и восемь четырнадцатых).

Ответ на вопрос «Из какой дроби можно выделить целую часть?» следующий. В правильной дроби числитель меньше знаменателя, следовательно, результат деления числителя на знаменатель меньше единицы. Поэтому из правильной дроби выделить целую часть нельзя. Целую часть можно выделить из неправильной дроби, в процессе её обращения в смешанное число. Эта процедура рассмотрена в примерах выше, а также наглядно показана в обучающем видео.

Обращение смешанного числа в неправильную дробь

Чтобы обратить смешанное число в неправильную дробь, нужно:

– знаменатель умножить на целую часть;

– к полученному произведению прибавить числитель, сделать эту сумму числителем искомой дроби, а знаменатель оставить прежний.

Ниже смешанные числа из предыдущих примеров (61/4 и 78/14) снова обращены в неправильные дроби:

Пример 1.

Требуется смешанное число 61/4 обратить в неправильную дробь.

6 (целых)*4 (знаменатель) = 24,

24 + 1 (числитель) = 25 (будет числителем неправильной дроби),

Неправильная дробь: 25/4.

Пример 2.

Требуется смешанное число 78/14 обратить в неправильную дробь.

7 (целых)*14 (знаменатель) = 98,

98 + 8 (числитель) = 106 (будет числителем неправильной дроби),

Неправильная дробь: 106/14.

Другие примеры.

63/4 = (6*4 + 3)/4 = (24+3)/4 = 27/4

53/8 = (5*8 + 3)/8 = (40+3) / 8 = 43/8

2514/88 = (25*88 + 14)/88 = (2200 + 14) / 88 = 2214/88

Основное свойство дроби

При одновременном увеличении или уменьшении числителя и знаменателя в одинаковое число раз дробь не изменится.

a/b = am / bm 

1/2 = 2/4 = 4/8

Представить себе это можно так. Разрезали торт на четыре равные части, и одну взяли себе. Т.е. взяли ¼ торта. Но каждый кусок можно ещё разрезать, например, пополам (а весь торт при этом был бы разрезан не на 4, а на 8 равных частей). Наша доля осталась бы прежней (1/4), но состояла бы она из двух кусков меньшей в два раза величины (т.е. 2/8). Или торт можно было бы разрезать не на 4 и не на 8, а на 12 равных частей. Взяли бы мы тогда себе 3 куска (т.е. 3/12). Но и 2/8, и 3/12 составляет ту же ¼ часть торта. Ни больше, ни меньше.

Как и зачем сокращать дроби

Сокращением дроби называется замена её другой, равной ей дробью с меньшими членами, путём деления числителя и знаменателя на одно и то же число.

Таким образом, сокращение дроби основано на основном её свойстве.

Зачем сокращать дроби? Взятую часть торта из предыдущего примера (3/12 или 2/8) легче представить в своём воображении, если эти дроби сократить. В дроби 3/12 и числитель, и знаменатель делятся без остатка на 3, результат – ¼. В дроби 2/8 и числитель, и знаменатель делятся без остатка на 2, результат – ¼. Представить ¼ торта гораздо легче, чем представить 2/8, 3/12 или же 6/24 торта.

Другие примеры сокращения дробей:

18/56 = (2*9) / (2*28) = 9/28

27/33 = (3*9) / (3*11) = 9/11

30/250 = (3*10) / (25*10) = 3/25

Иногда задают вопрос «Можно ли сокращать дроби при их сложении и вычитании?». Можно и нужно сокращать эти дроби, только ни в коем случае не «друг с другом», т.е. не числитель одной дроби со знаменателем другой. Сокращать нужно каждую дробь в отдельности, но нужно при этом помнить и о том, что дроби для их сложения или вычитания должны быть приведены к одному общему знаменателю (и желательно – именно к наименьшему общему знаменателю). А вот при умножении дробей сокращать можно числитель дроби со знаменателем как этой дроби, так и со знаменателем другой дроби. Поскольку деление дробей заменяется операцией умножения, то сказанное выше можно распространить и на операцию деления дробей. Рекомендуется скачать решенные примеры с дробями, где были выполнены такие преобразования.

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить прежний.

Например,

3/5 + 1/5 = 4/5 (сложили числители 3 + 1 = 4, а знаменатель (5) оставили прежний).

Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно вычесть числитель вычитаемого из числителя уменьшаемого, а знаменатель дроби оставить прежний.

Например,

6/15 – 4/15 = 2/15 (числитель 6 – 4 = 2, знаменатель (15) прежний).

Приведение дробей к наименьшему общему знаменателю

Чтобы выполнить сложение или вычитание дробей, имеющих разные знаменатели, нужно предварительно привести их к общему знаменателю. Этим знаменателем должно стать общее кратное знаменателей данных дробей.

Например, дроби 2/5 и 3/15 можно было бы привести к общему знаменателю 15, 30, 45, 75, 150 или ещё большему, но объем вычислительной работы будет намного меньшим, если приводить дроби именно к наименьшему общему знаменателю (в данном случае — 15).

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

– найти наименьшее общее кратное всех знаменателей;

– для каждого знаменателя определить дополнительный множитель (разделив новый знаменатель на прежний);

– числитель и знаменатель каждой дроби умножить на соответствующий дополнительный множитель её знаменателя.

Пример 1.

Дроби 2/5 и 3/15.

Знаменатель первой дроби: 5 = 1*5

Знаменатель второй дроби: 15 = 3*5

Наименьшее общее кратное знаменателей: 3*5 = 15 (новый знаменатель дробей)

Дополнительный множитель для знаменателя первой дроби: 15 / 5 = 3

Дополнительный множитель для знаменателя второй дроби: 15 / 15 = 1

Новый числитель первой дроби: 3*2 = 6

Новый числитель второй дроби: 3 (в данном случае первая дробь приводится к знаменателю второй дроби).

Итак, ответ: 6/15 и 3/15.

Пример 2.

Дроби 2/5 и 4/7.

Знаменатель первой дроби: 5 = 1*5

Знаменатель второй дроби: 7 = 1*7

Наименьшее общее кратное знаменателей: 5*7 = 35 (новый знаменатель дробей)

Дополнительный множитель для знаменателя первой дроби: 35 / 5 = 7

Дополнительный множитель для знаменателя второй дроби: 35 / 7 = 5

Новый числитель первой дроби: 7*2 = 14

Новый числитель второй дроби: 5*4 = 20.

Итак, ответ: 14/35 и 20/35.

Пример 3.

Дроби 2/15 и 7/12.

Знаменатель первой дроби: 15 = 3*5

Знаменатель второй дроби: 12 = 3*4

Наименьшее общее кратное знаменателей: 3*4*5 = 60 (новый знаменатель дробей)

Дополнительный множитель для знаменателя первой дроби: 60 / 15 = 4

Дополнительный множитель для знаменателя второй дроби: 60 / 12 = 5

Новый числитель первой дроби: 4*2 = 8

Новый числитель второй дроби: 5*7 = 35.

Итак, ответ: 8/60 и 35/60.

Пример 4.

Дроби 2/21, 5/24 и 3/16.

Знаменатель первой дроби: 21 = 3*7

Знаменатель второй дроби: 24 = 2*12 = 2*2*6 = 2*2*2*3

Знаменатель третьей дроби: 16 = 2*8 = 2*2*4 = 2*2*2*2

Наименьшее общее кратное знаменателей: 2*2*2*2*3*7= 336 (новый знаменатель дробей)

Дополнительный множитель для знаменателя первой дроби: 336 / 21 = 16

Дополнительный множитель для знаменателя второй дроби: 336 / 24 = 14

Дополнительный множитель для знаменателя третьей дроби: 336 / 16 = 21

Новый числитель первой дроби: 2*16 = 32

Новый числитель второй дроби: 5*14 = 70

Новый числитель третьей дроби: 3*21 = 63

Итак, ответ: 32/336, 70/336 и 63/336.

Сложение и вычитание дробей с разными знаменателями (т.е. сложение и вычитание дробей, имеющих разные знаменатели)

Чтобы сложить дроби с разными знаменателями, нужно предварительно привести их к наименьшему общему знаменателю, сложить их числители и подписать общий знаменатель.

Например, нужно сложить дроби 2/21, 5/24 и 3/16.

Приведение их к наименьшему общему знаменателю подробно описано в рассмотренном выше примере №4.

Таким образом,

2/21 + 5/24 + 3/16 = 32/336 + 70/336 + 63/336 = (32 + 70 + 63)/336 = 165/336

Сложение дробей с разными знаменателями (т.е. сложение дробей, имеющих разные знаменатели)

Чтобы сложить дроби с разными знаменателями, нужно предварительно привести их к наименьшему общему знаменателю, сложить их числители и подписать общий знаменатель.

Например, нужно сложить дроби 2/21, 5/24 и 3/16.

Приведение их к наименьшему общему знаменателю подробно описано в рассмотренном выше примере №4.

Таким образом,

2/21 + 5/24 + 3/16 = 32/336 + 70/336 + 63/336 = (32 + 70 + 63)/336 = 165/336.

Рекомендуется скачать решенные примеры с дробями, где были выполнены действия сложения дробей с разными знаменателями.

Вычитание дробей с разными знаменателями (т.е. вычитание дробей, имеющих разные знаменатели)

Чтобы вычесть дроби с разными знаменателями, нужно предварительно привести их к наименьшему общему знаменателю, вычесть числитель вычитаемого из числителя уменьшаемого и подписать общий знаменатель.

Пример:

5/24 – 2/21 = 70/336 – 32/336 = 38/336.

Оставлять ответ в таком виде математически «некультурно». Дробь нужно сократить: 38/336 = (2*19) / (2*168) = 19/168. Однако, сокращать дробь пришлось из-за того, что знаменатель 336 был наименьшим общим знаменателем трех дробей 2/21 + 5/24 + 3/16, рассмотренных в предыдущем примере, но не является наименьшим общим знаменателем дробей двух дробей 5/24 и 2/21 (а является просто общим знаменателем).

А поступить изначально следовало так:

24 = 2*12 = 2*2*6 = 2*2*2*3

21 = 3*7

НОК(24,21) = 2*2*2*3*7 = 168 (наименьший общий знаменатель дробей 5/24 и 2/21)

168/24*5 = 7*5 = 35 (числитель первой дроби)

168/21*2 = 8*2 = 16 (числитель второй дроби)

5/24 – 2/21 = 35/168 – 16/168 = 19/168.

Получен тот же ответ, но быстрее и оперируя меньшими числами.

Итак, ответ: 5/24 – 2/21 = 19/168.

Рекомендуется скачать решенные примеры с дробями, где были выполнены действия вычитания дробей с разными знаменателями.

Сравнение дробей

Чтобы сравнить дроби, имеющие одинаковые знаменатели, нужно сравнить числители этих дробей.

Например,

2/5 < 4/5,

7/18 > 1/18.

Чтобы сравнить дроби, имеющие разные знаменатели, нужно привести их к общему знаменателю, и затем сравнить новые числители дробей. Лучше приводить дроби к наименьшему общему знаменателю, так намного сокращается объем вычислительной работы.

Пример.

Нужно сравнить дроби 2/21 и 3/16.

21 = 3*7

16 = 2*2*2*2

НОК(21, 16) = 2*2*2*2*3*7 = 336

2/21 = 32/336

3/16 = 63/336

63>32, следовательно дробь 63/336 больше дроби 32/336, и 3/16> 2/21, а 2/21 < 3/16.

Сложение и вычитание смешанных чисел

Иногда вопросы задают так: «Как складывать смешанные дроби?», «Как вычитать смешанные дроби?». Это некорректно. Есть дробные числа, которые и называют просто «дробями» (например, 5/7 или 8/49), а есть смешанные числа, состоящие из целой и дробной части (например, 18/9, 12513/14). Нет такого понятия «смешанная дробь». Вопрос должен звучать так: «Как складывать смешанные числа?» или «Как вычитать смешанные числа?».

Последовательно нужно сложить (вычесть) целые и дробные части. При необходимости, дробные части нужно привести к общему знаменателю.

Бывают случаи, когда дробная часть вычитаемого больше дробной части уменьшаемого. В таких случаях нужно взять одну единицу из целой части уменьшаемого, раздробить её в те доли, в каких выражена дробная часть, и прибавить к дробной части уменьшаемого.

Примеры.

51/8 + 3/8 = 54/8 = 51/2

102/21 + 5/24 + 63/16 = 1032/336 + 70/336 +663/336 = 10 + 6 + (32 + 70 + 63)/336 = 16 + 165/336 = 16165/336.

53/16 – 12/21 = 5 – 1 + 3/16 – 2/21 = 4 + 63/336 — 32/336 = 4 + (63 — 32)/336 = 4 + 31/336 = 431/336

72/21 – 33/16 = 7 – 3 + 2/21 – 3/16 = 4 + 32/336 — 63/336 = 3 + 1 + 32/336 – 63/336 = 3 + 336/336 + 32/336 – 63/336 = 3 + (336 + 32 — 63)/336 = 3 + 305/336 = 3305/336

Поскольку вопрос «Как складывать дроби с целым числом» кто-то может трактовать ошибочно, ответ на этот вопрос здесь рассматривается подробно. Если имеется в виду прибавление дроби к целому числу (например, к двум нужно прибавить две трети, т.е. 2 + 2/3), то ответ будет представлять собой смешанное число, целая часть которого равна целому числу – слагаемому (в настоящем примере это число «2»), а дробная часть равна дроби (в настоящем примере это 2/3). Т.е. 2 + 2/3 = 22/3. Другой пример: 15 + 7/24 = 157/24. Если же в данном вопросе кто-то под фразой «дробь с целым числом» понимает смешанное число – это некорректно. Тогда вопрос нужно ставить как «сложение смешанных чисел», «как складывать смешанные числа».

Рекомендуется скачать решенные примеры с дробями, где было выполнено сложение и вычитание смешанных чисел.

Умножение целого числа на дробь

Чтобы умножить целое число на дробь, надо умножить целое число на числитель этой дроби и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби.

Аналогично, чтобы умножить дробь на целое число, надо умножить числитель дроби на целое число и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби.

Пример.

3* 5/8 = (3*5) / 8 = 15/8 = 17/8

Умножение дробей

При умножении дробей нет никакой разницы в том, одинаковы их знаменатели или же они различные. Поэтому вопросы «как умножать дроби с одинаковыми знаменателями», «как умножать дроби с разными знаменателями» и «как умножать дроби с разными знаменателями и числителями» особого смысла не имеют. Ответы на них те же, что и на известные, более распространенные вопросы «как умножать дроби», «как умножить дробь на дробь».

Правило умножения дробей следующее.

Чтобы умножить дробь на дробь, нужно умножить числитель на числитель (это будет числитель произведения), а знаменатель – на знаменатель (это будет знаменатель произведения).

Пример:

2/3 * 5/6 = (2*5) / (3*6) = 10/18

Дробь 10/18 нужно ещё сократить: 10/18 = (2*5) / (2*9) = 5/9.

Но можно было поступить иначе (что предпочтительней):

2/3 * 5/6 = (2*5) / (3*6) = (2*5) / (3*2*3) = 5 / (3*3) = 5/9

Если один или несколько сомножителей имеют знак «минус» — знак произведения определяют так же, как и при умножении целых чисел с разными знаками.

Умножение смешанного числа на целое число

Чтобы умножить смешанное число на целое, нужно предварительно обратить смешанное число в неправильную дробь и потом перемножить по правилу умножения дроби на целое число.

Примеры.

21/3 * 4 = 7/3 * 4 = (7*4) / 3 = 28/3 = 91/3

6 * 58/9 = 6 * (5*9 + 8)/9 = 6* (45+8)/9 = 6* 53/9 = 2*3*53/(3*3) = 2*53/3 = 106/3 = 351/3

Как известно, к множеству целых чисел относятся натуральные числа, им противоположные (т.е. со знаком «минус») и ноль. Поэтому умножение смешанного числа на натуральное число – это частный случай, на который так же распространяется правило умножения смешанного числа на целое число. Иногда этот вопрос формулируют некорректно: как умножать смешанные дроби на натуральное число. Нет понятия «смешанные дроби», есть смешанные числа.

Умножение смешанных чисел

Иногда вопрос задают так: «Как умножать смешанные дроби?». Это некорректно, как уже было сказано выше, когда разбирались подобные некорректные вопросы о сложении и умножении смешанных дробей. Вопрос должен звучать так: «Как умножать смешанные числа?».

Чтобы перемножить смешанные числа, нужно предварительно обратить их в неправильные дроби и потом перемножить по правилу умножения дроби на дробь.

Пример.

27/8 * 35/11 = [(2*8 + 7)/8] * [(3*11 + 5)/11] = [(16+7)/8] * [(33+5)/11] = 23/8 * 38/11 = [23/(2*4)] * [(2*19)/11] = 23/4 * 19/11 = (23*19) / (4*11) = 437 / 44 = 941/44

Здесь в процессе решения было выполнено сокращение дробей (уменьшение числителя и знаменателя в одинаковое число раз, в данном случае – в два раза). Если бы этого не было сделано в процессе решения, а были бы просто перемножены числители и знаменатели, результат был бы следующим:

27/8 * 35/11 = 23/8 * 38/11 = (23*38) / (8*11) = 874/88

Как видно, такую дробь нужно сокращать:

27/8 * 35/11 = 23/8 * 38/11 = 874/88 = (437*2)/(44*2) = 437/44

Этим примером проиллюстрировано, что, не производя сокращение дробей в процессе решения, приходится оперировать большими числами, а дробь, полученную в результате, так же приходится сокращать. Лучше производить сокращение в процессе решения.

Рекомендуется скачать решенные примеры с дробями, где было выполнено умножение смешанных чисел.

Вопрос «Как умножать дроби с целым числом» некорректен. Если под «дробью с целым числом» имеется в виду смешанное число – читайте об умножении смешанных чисел. Если же имеется в виду умножение дроби на целое число – читайте о том, как умножить целое число на дробь.

Обратные дроби

Понимание того, что такое обратная дробь, весьма важно для освоения процедуры деления дробей. Взаимно обратными дробями называются две дроби, обладающие тем свойством, что числитель первой является знаменателем второй, а знаменатель первой является числителем второй.

Например, взаимно обратными являются дроби 4/5 и 5/4, 11/148 и 148/11.

Для всех чисел с числителем «1» обратными будут целые числа. А чтобы написать число, обратное целому, надо поставить это число знаменателем, а числителем будет равен 1.

Например, взаимно обратными будут числа 7 и 1/7, 25 и 1/25, 1/48 и 48, 1/3 и 3.

Взаимно обратные числа обладают следующим свойством: произведение взаимно обратных чисел равно единице.

Деление целого числа на дробь

Чтобы разделить число на дробь, надо это целое число умножить на знаменатель данной дроби и, сделав это произведение числителем, разделить его на числитель данной дроби.

Это правило можно записать так:

a: (b/c) = (ac) / b

Примеры:

5/ (2/3) = (5*3)/2 = 15/2 = 71/2

8/ (6/21) = (8*21) / 6 = (2*4*21) / (2*3) = (4*21) / 3 = (4*3*7) / 3 = 4*7 = 28

Деление дробей

При делении дробей не имеет значения, одинаковы или различны их знаменатели. Поэтому вопросы «Как делить дроби с разными знаменателями и числителями», «Как делить дроби с разными знаменателями», «Как делить дроби с одинаковыми знаменателями» особого смысла не имеют. Ответы на них те же, что и на вопрос о том, как делить дроби.

Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй (это будет числитель новой дроби), а знаменатель первой дроби умножить на числитель второй (это будет знаменатель новой дроби).

Можно сказать иначе:

Чтобы разделить дробь на дробь, нужно первую дробь (делимое) умножить на дробь, обратную второй (делителю) (т.е. первую дробь нужно умножить на «перевернутую» вторую дробь).

Примеры:

(4/5):(3/11) = (4/5)*(11/3) = (4*11)/(5*3) = 44/15 = 214/15

(6/7):(2/9) = (4/5)*(11/3) = (4*11)/(5*3) = 44/15 = 214/15

О том, как работать с буквенно-числовыми выражениями (делить их, вычитать, умножать, складывать), говорится в школьном курсе алгебры. Этот вопрос не затрагивается в данной статье, посвященной обыкновенным и десятичным дробям. Однако, даётся предостережение: иногда школьники ошибочно «делят» sin(x) на cos(x), сокращают одинаковые буквы «s» и одинаковые буквы «х» в числителе и знаменателе и получают «результат» in/co. Это абсолютно безграмотно, т.к. sin(x) и cos(x) – тригонометрические функции, а не произведение переменных «s», «i», «n», «x» и «c», «o», «s», «x».

Если делимое или делители имеют знак «минус» — знак частного определяют так же, как и при делении целых чисел с разными знаками.

Деление смешанных чисел

Иногда вопрос задают так: «Как делить смешанные дроби?». Выше уже было сказано о том, что понятия «смешанная дробь» нет. Вопрос должен звучать так: «Как делить смешанные числа?».

Чтобы разделить одно смешанное число на другое, нужно предварительно обратить их в неправильные дроби и потом разделить по правилу деления дроби на дробь.

Пример.

27/8 : 35/11 = [(2*8 + 7)/8] : [(3*11 + 5)/11] = [(16+7)/8] : [(33+5)/11] = 23/8 : 38/11 =

=(23/8) * (11/38) = (23*11) / (8*38) = 253 / 304.

Рекомендуется скачать решенные примеры с дробями, где было выполнено деление дробей и деление смешанных чисел. Там же можно скачать примеры решений с трехэтажными дробями.

Десятичные дроби

Различают дроби обыкновенные и дроби десятичные. Обыкновенные дроби представлены в виде числителя и знаменателя, разделенных горизонтальной чертой. Когда нет возможности поставить горизонтальную черту, пользуются косой чертой (например, 7/11, 6/125, 39/1572). Знаменателями же десятичных дробей являются только числа, изображаемые единицей с последующими нулями (одним или несколькими), например 7/10, 6/100, 39/1000. Те же 7/10, 6/100 и 39/1000 можно представить в виде десятичной дроби без знаменателя: 0,7; 0,06; 0,039 (читается: семь десятых, шесть сотых, тридцать девять тысячных).

Сравнение десятичных дробей

Из двух десятичных дробей та больше, у которой число целых больше; при равенстве целых та дробь больше, у которой число десятых больше; при равенстве целых и десятых та дробь больше, у которой число сотых больше, и т.д.

Например,

3,125 < 5,016

0,078 > 0,069

0,412 > 0,300257

0,7825 < 0,784

0,905 < 0,92

Действия над десятичными дробями

Чтобы увеличить десятичную дробь в 10 раз, нужно перенести запятую в ней на один знак вправо; чтобы увеличить её в 100 раз, нужно перенести запятую на два знака вправо; чтобы увеличить её в 1000 раз – на три знака вправо, и т.д. Если при этом не хватает знаков у числа, то приписывают к нему справа нули.

Чтобы уменьшить десятичную дробь в 10 раз, нужно перенести запятую в ней на один знак влево; чтобы уменьшить её в 100 раз, нужно перенести запятую на два знака влево; чтобы уменьшить её в 1000 раз – на три знака влево, и т.д. Если при этом не хватает знаков у числа, то приписывают к нему слева нули.

Например,

2,05*10 = 20,5

2,05*1000 = 2050

2,05/10 = 0,205

2,05/100 = 0,0205 

При сложении десятичных дробей надо соблюдать следующий порядок: дроби подписывать одна под другой так, чтобы во всех слагаемых одинаковые разряды находились друг под другом и все запятые стояли в одном и том же вертикальном столбце; справа от десятичных знаков некоторых слагаемых приписывают, хотя бы мысленно, такое число нулей, чтобы все слагаемые после запятой имели одинаковое число цифр. Затем выполняют сложение по разрядам, начиная с правой стороны, и в полученной сумме ставят запятую в том же самом вертикальном столбце, в каком она находится в данных слагаемых.

Например, требуется сложить 1,905 + 0,3 + 7,8814

  1,9050

  0,3000

  7,8814

10,0864

При вычитании десятичных дробей надо соблюдать следующий порядок: подписывают вычитаемое под уменьшаемым так, чтобы одинаковые разряды находились друг под другом и все запятые стояли в одном и том же вертикальном столбце; справа приписывают, хотя бы мысленно, в уменьшаемом или вычитаемом столько нулей, чтобы они имели одинаковое число десятичных знаков, затем выполняют вычитание по разрядам, начиная с правой стороны, и в полученной разности ставят запятую в том же самом вертикальном столбце, в каком она находится в уменьшаемом и вычитаемом.

Например, требуется выполнить вычитание 145,501 – 3,040652 – 17,89

145,501000

    3,040652

  17,890000

124,570348

Чтобы перемножить две десятичные дроби, достаточно, не обращая внимания на запятые, перемножить их как целые числа и в произведении отделить запятой с правой стороны столько десятичных знаков, сколько их было во множимом и множителе вместе.

Например,

127,0206*4,03 = 511,893018

7,31*2,4 = 17,544

Деление десятичной дроби на целое число выполняется так же, как и деление целых чисел, причём получающиеся остатки обращают в десятичные доли, всё боле и более мелкие; деление продолжают до тех пор, пока в остатке не получится нуль или остаток не станет пренебрежимо малым (исходя из его разряда).

Чтобы разделить число на десятичную дробь, нужно отбросить в делителе запятую, а затем увеличить делимое во столько раз, во сколько увеличился делитель при отбрасывании в нём запятой, после чего выполнить деление по правилу деления на целое число.

Например, 5/3,05 = 500/305 ≈ 1,639344

Зачем в школе изучают дроби

Тема «дроби» довольно тяжело дается почти всем школьникам, исключение составляют лишь 3 – 5 человек из класса, наиболее сообразительные и наиболее подготовленные к обучению в школе. Но и все остальные могут (и должны) её освоить путем систематических занятий, решения достаточного количества примеров, способствующих выработке техники вычислений, и задач, способствующих более глубокому пониманию данной темы. Ведь дроби окружают нас в жизни всюду: разве есть человек, не знающий о существовании пол-литровой (0,5 л или ½ л) банки или о том, что нормальная температура его тела должна составлять 36,6 градусов? И, на самом деле, каждый знает, что содержимое двух пол-литровых банок можно слить в одну литровую, а содержимое двух 1,5 л бутылок – в трёхлитровую бутыль, просто в этот момент никто не задумывается о том, что он сейчас складывает дроби. А разве кто-то не умеет сравнивать десятичные дроби? Есть кто-то, не знающий, что температура тела 36,9 – выше, чем 36,6? Но это – лишь самые простые примеры из повседневной жизни любого человека. Людям же технических и естественно-научных специальностей приходится в своей профессиональной деятельности решать более сложные задачи, связанные с дробными числами. Понимание темы «дроби» очень пригодится и при дальнейшем изучении математики в средней школе, т.е. алгебры и геометрии. 

Примеры решения задач на действия с дробями

Задача 1

В первый день стекольщики остеклили 35 окон, что составляет 1/8 всех окон построенного дома. Сколько всего окон в доме? 

В условии задачи сказано, что остекленные 35 окон составляют 1/8 всех окон построенного дома. Значит, всего окон в 8 раз больше, т.е.

35*8 = 280 окон.

Задача 2

Магазин за месяц продал 2730 кг сахара, что составляет 3/7 всего запаса сахара, имевшегося в магазине. Каков был первоначальный запас сахара в магазине?

Весь имевшийся запас – это 7/7.

1/7 запаса составляет 2730/3 = 910 кг.

Весь имевшийся запас составлял 910*7 = 6370 кг.

Источники информации:

  • Шевченко И.Н. Арифметика. Учебник для 5 и 6 классов восьмилетней и средней школы. – Изд. 8-е. – М.: Гос. учебно-педагогическое изд., 1963. – 216 с.
  • Выгодский М.Я. Справочник по элементарной математике. – М.: Государственное издательство технико-теоретической литературы. – 412 с. 
  • Универсальная школьная энциклопедия. В 2-х томах. Т. 1 (А – Л) / Под ред. Е. Хлебалиной. — М.:Аванта+, 2003. — 528 с.
  • reshusam.ucoz.ru — Примеры выполнения действий с дробями;
  • ru.wikipedia.org — дробь (математика) — Википедия;
  • dic.academic.ru — дробь (математика);
  • for6cl.uznateshe.ru — что такое дробь. Математика.

    •  

Источник

Добавить комментарий