Как найти сумму двадцатиугольника

Как найти сумму двадцатиугольника

Двадцатиугольник
Правильный двадцатиугольник
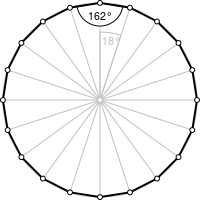Правильный двадцатиугольник
Тип Правильный многоугольник
Рёбра 20
Символ Шлефли {displaystyle {20},mathrm {t} {10},mathrm {tt} {5}}
Диаграмма Коксетера — Дынкина CDel node 1.pngCDel 20.pngCDel node.png
CDel node 1.pngCDel 10.pngCDel node 1.png
Вид симметрии Диэдрическая группа ({displaystyle D_{20}})
Площадь {displaystyle 5t^{2}(1+{sqrt {5}}+{sqrt {5+2{sqrt {5}}}})}
Внутренний угол {displaystyle 162^{circ }}
Свойства
выпуклый, вписанный, равносторонний, равноугольный[en], изотоксальный
Логотип Викисклада Медиафайлы на Викискладе

Двадцатиугольник – это многоугольник с двадцатью сторонами и двадцатью углами. Сумма внутренних углов любого двадцатиугольника составляет 3240 градусов.

Правильный двадцатиугольник[править | править код]

Правильный двадцатиугольник имеет символ Шлефли {displaystyle {20}}, и может быть построен как усечённый десятиугольник, {displaystyle mathrm {t} {10}}, или дважды усечённый пятиугольник, {displaystyle mathrm {tt} {5}}.

Каждый из внутренних углов в правильном двадцатиугольнике равен {displaystyle 162^{circ }}, а это значит, что каждый из внешних углов равен {displaystyle 18^{circ }}.

Площадь правильного двадцатиугольника с длиной стороны t равна

{displaystyle A={5}t^{2}(1+{sqrt {5}}+{sqrt {5+2{sqrt {5}}}})simeq 31.5687cdot t^{2}.}

Площадь многоугольника, выраженная через радиус R его описанной окружности равна

{displaystyle A={frac {5R^{2}}{2}}({sqrt {5}}-1);}

Поскольку площадь круга равна {displaystyle pi R^{2},} правильный двадцатиугольник заполняет примерно {displaystyle 98,36~%} своей описанной окружности.

Построение[править | править код]

Так как {displaystyle 20=2^{2}cdot 5}, правильный двадцатиугольник можно построить при помощи циркуля и линейки, или при помощи разбиения сторон правильного десятиугольника, или двойного разбиения сторон правильного пятиугольника.

Золотое сечение в правильном двадцатиугольнике[править | править код]

Построение правильного двадцатиугольника с заданной длиной стороны

{displaystyle {frac {overline {E_{20}E_{1}}}{overline {E_{1}F}}}={frac {overline {E_{20}F}}{overline {E_{20}E_{1}}}}={frac {1+{sqrt {5}}}{2}}=Phi approx 1.618}

Симметрия[править | править код]

Группы симметрий правильного двадцатиугольника. Симметричные вершины окрашены в одинаковые цвета. Голубые зеркала проведены через вершины, фиолетовые — через стороны. Порядки групп вращений даны в центре.

Симметрии правильного двадцатиугольника образуют диэдральную группу {displaystyle mathrm {D} _{20}}. В ней можно выделить пять подгрупп диэдральных симметрий ({displaystyle mathrm {D} _{10},mathrm {D} _{5},mathrm {D} _{4},mathrm {D} _{2}} и {displaystyle mathrm {D} _{1}}), и шесть циклических подгрупп ({displaystyle mathrm {Z} _{20},mathrm {Z} _{10},mathrm {Z} _{5},mathrm {Z} _{4},mathrm {Z} _{2}} и {displaystyle mathrm {Z} _{1}}). Все различные подгруппы симметрий правильного двадцатиугольника могут быть графически отображены диаграммой из 16 элементов.

В данной диаграмме, предложенной Джоном Конвеем, каждая подгруппа симметрии обозначена буквой и собственным порядком.[1] Вся группа симметрий названа {displaystyle mathrm {r} 40}, а тривиальная подгруппа, соответствующая полному отсутствию симметрии, обозначена как {displaystyle mathrm {a} 1}. Диэдрические группы симметрии делятся на те, оси симметрий которых проходят только через вершины ({displaystyle mathrm {d} } — diagonal), только через рёбра ({displaystyle mathrm {p} } — perpendicular) или через и то, и другое (такая подгруппа обозначена буквой {mathrm {i}}). Циклические симметрии обозначены буквой {displaystyle mathrm {g} } (англ. gyration) и своим порядком.

Группа симметрий любого неправильного двадцатиугольника образует подгруппу {displaystyle mathrm {D} _{20}}. Среди них наиболее симметричными являются фигуры, соответствующие симметриям {displaystyle mathrm {d} 20} (изогональный двадцатиугольник, построенный при помощи десяти зеркал с чередованием длинных и коротких рёбер) и {displaystyle mathrm {p} 20} (изотоксальный двадцатиугольник, в котором все стороны равны между собой, но внутренние углы при вершинах чередуются). Эти две формы двойственны[en] друг другу и каждая из них обладает половиной симметрий правильного двадцатиугольника.

Разбиения[править | править код]

Двадцатиугольник, разбитый на 180 ромбов

20-gon rhombic dissection-size2.svg
Правильное разбиение 		Isotoxal 20-gon rhombic dissection-size2.svg
Изотоксальное разбиение

По Коксетеру, любой зоногон (2m-угольник, у которого противоположные стороны равны и параллельны друг другу) может быть разбит на {displaystyle m(m-1)/2} параллелограммов[2]. В частности, это так для всех правильных многоугольников с чётным числом сторон — в этом случае все параллелограммы являются ромбами. Для двадцатиугольника {displaystyle m=10}, а значит, его можно разбить на {displaystyle 45} параллелограммов: 5 квадратов и 4 набора ромбов — по 10 в каждом. Это разбиение основано на проекции Декеракта в виде многоугольника Петри с {displaystyle 45} гранями из {displaystyle 11520}. Согласно данным из последовательности A006245, количество всевозможных описанных разбиений 20-угольника равно {displaystyle 18410581880}, если зеркальные и повёрнутые копии разбиения считать различными.

Изображение декеракта и примеры разбиения 20-угольника на 45 ромбов

10-cube.svg
Декеракт 		20-gon-dissection.svg 20-gon rhombic dissection2.svg 20-gon rhombic dissectionx.svg 20-gon-dissection-random.svg

Связанные многоугольники[править | править код]

Икосаграмма — звёздчатый многоугольник с двадцатью сторонами, имеющий символ Шлефли {displaystyle {20/n}}. Есть три правильных икосаграммы с символами Шлефли {displaystyle {20/3}}, {displaystyle {20/7}} и {displaystyle {20/9}}. Есть также ещё 5 звёздчатых многоугольников с тем же относительным расположением вершин: {displaystyle 2{10}}, {displaystyle 4{5}}, {displaystyle 5{4}}, {displaystyle 2{10/3}}, {displaystyle 4{5/2}} и {displaystyle 10{2}}.

n 1 2 3 4 5
Форма Выпуклый многоугольник Составной Звёздчатый многоугольник Составной
Фото Regular polygon 20.svg
{displaystyle {20/1}={20}} 		Regular star figure 2(10,1).svg
{displaystyle {20/2}=2{10}} 		Regular star polygon 20-3.svg
{displaystyle {20/3}} 		Regular star figure 4(5,1).svg
{displaystyle {20/4}=4{5}} 		Regular star figure 5(4,1).svg
{displaystyle {20/5}=5{4}}
Внутренний угол {displaystyle 162^{circ }} {displaystyle 144^{circ }} {displaystyle 126^{circ }} {displaystyle 108^{circ }} 90^{circ }
n 6 7 8 9 10
Форма Составной Звёздчатый многоугольник Составной Звёздчатый многоугольник Составной
Фото Regular star figure 2(10,3).svg
{displaystyle {20/6}=2{10/3}} 		Regular star polygon 20-7.svg
{displaystyle {20/7}} 		Regular star figure 4(5,2).svg
{displaystyle {20/8}=4{5/2}} 		Regular star polygon 20-9.svg
{displaystyle {20/9}} 		Regular star figure 10(2,1).svg
{displaystyle {20/10}=10{2}}
Внутренний угол {displaystyle 72^{circ }} {displaystyle 54^{circ }} {displaystyle 36^{circ }} {displaystyle 18^{circ }} 0^{circ }

Более глубокие усечения правильного десятиугольника и декаграммы могут привести к изогональным (вершинно-транзитивным) промежуточным формам икосаграмм с одинаково расположенными вершинами и двумя длинами ребер.[3]

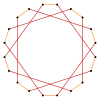
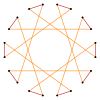
Правильную икосаграмму {20/9} можно рассматривать как квазиусеченный десятиугольник, t{10/9}={20/9}. Аналогично декаграмма {10/3} имеет квазиусечение t{10/7}={20/7}, и, наконец, простое усечение декаграммы дает t{10/3}={20/3}.

Икосаграммы, как усечения правильных десятиугольников и декаграмм, {10}, {10/3}.

Квазирегулярный Квазирегулярный
Regular polygon truncation 10 1.svg
t{10}={20} 		Regular polygon truncation 10 2.svg Regular polygon truncation 10 3.svg Regular polygon truncation 10 4.svg Regular polygon truncation 10 5.svg Regular polygon truncation 10 6.svg
t{10/9}={20/9}
Regular star truncation 10-3 1.svg
t{10/3}={20/3} 		Regular star truncation 10-3 2.svg Regular star truncation 10-3 3.svg Regular star truncation 10-3 4.svg Regular star truncation 10-3 5.svg Regular star truncation 10-3 6.svg
t{10/7}={20/7}

Многоугольники Петри[править | править код]

Правильный двадцатиугольник является многоугольником Петри для ряда политопов, что показано в ортогональных проекциях на плоскость Коксетера[en]:

A19 B10 D11 E8 H4 ½2H2 2H2
19-simplex t0.svg
19-симплекс 		10-cube t9.svg
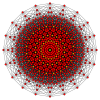10-ортоплекс[en] 		10-cube t0.svg
Декеракт 		11-demicube.svg
11-полукуб 		4 21 t0 p20.svg
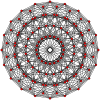(421) 		600-cell t0 p20.svg
Шестисотячейник 		Grand antiprism 20-gonal orthogonal projection.png
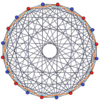Великая антипризма[en] 		10-10 duopyramid ortho-3.png
10-10 дуопирамида[en] 		10-10 duoprism ortho-3.png
10-10 дуопризма

Он также является многоугольником Петри для икосаэдрального 120-ячейника[en], малого звездчатого 120-ячейника[en], великого икосаэдрического 120-ячейника[en] и большого великого 120-ячейника[en].

Примечания[править | править код]

  1. ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
  2. ↑ Коксетер, Mathematical recreations and Essays, Thirteenth edition, p.141
  3. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Источник

Голосование за лучший ответ

Татьяна Козлова

Искусственный Интеллект

(331335)


8 лет назад

20 -угольник можно разрезать диагоналями на 18 треугольников, сумма углов треугольника 180, отсюда вывод 18х180=3240

Семен АркадьевичВысший разум (340149)

8 лет назад

А зачем же так сложно ?) Почему бы не разрезать на 20 треугольников и вычесть углы сошедшиеся в центре ?))

Татьяна Козлова
Искусственный Интеллект
(331335)
По моему репетиторскому опыту – почему-то мои ученики режут именно диагоналями, когда предлагаю им придумать способ подсчета))

Источник

Есть теорема о сумме углов мноугольника — которая состоит из данного определения: Зная количество углов многоугольника — сумма этих же углов равняется:

Вывод: Сумма углов двадцатиугольника равна: 3240°.

2.

Так как двадцатиугольник — правильный, то его все углы, очевидно: равны.

И так как сумма углов нам уже известна, то каждый угол по отдельности будет равнятся:

Вывод: Градусная мера угла двадцатиугольника равна: 162°.

Источник
Двадцатиугольник
Правильный двадцатиугольникПравильный двадцатиугольник
Тип Правильный многоугольник
Рёбра [math]displaystyle{ 20 }[/math]
Символ Шлефли [math]displaystyle{ {20}, mathrm{t}{10}, mathrm{tt}{5} }[/math]
Диаграмма Коксетера — Дынкина CDel node 1.pngCDel 20.pngCDel node.png
CDel node 1.pngCDel 10.pngCDel node 1.png
Вид симметрии Диэдрическая группа ([math]displaystyle{ D_{20} }[/math])
Площадь [math]displaystyle{ 5t^2 (1 + sqrt{5}+sqrt{5 + 2sqrt{5}}) }[/math]
Внутренний угол [math]displaystyle{ 162^circ }[/math]
Свойства
выпуклый, вписанный, равносторонний, равноугольный[en], изотоксальный

Двадцатиугольник – это многоугольник с двадцатью сторонами и двадцатью углами. Сумма внутренних углов любого двадцатиугольника составляет [math]displaystyle{ 3240^{circ} }[/math].

Правильный двадцатиугольник

Правильный двадцатиугольник имеет символ Шлефли [math]displaystyle{ {20} }[/math], и может быть построен как усечённый десятиугольник, [math]displaystyle{ mathrm{t}{10} }[/math], или дважды усечённый пятиугольник, [math]displaystyle{ mathrm{tt}{5} }[/math].

Каждый из внутренних углов в правильном двадцатиугольнике равен [math]displaystyle{ 162^{circ} }[/math], а это значит, что каждый из внешних углов равен [math]displaystyle{ 18^{circ} }[/math].

Площадь правильного двадцатиугольника с длиной стороны [math]displaystyle{ t }[/math] равна

[math]displaystyle{ A={5}t^2(1+sqrt{5}+sqrt{5+2sqrt{5}}) simeq 31.5687cdot t^2. }[/math]

Площадь многоугольника, выраженная через радиус [math]displaystyle{ R }[/math] его описанной окружности равна

[math]displaystyle{ A=frac{5R^2}{2}(sqrt{5}-1); }[/math]

Поскольку площадь круга равна [math]displaystyle{ pi R^2, }[/math] правильный двадцатиугольник заполняет примерно [math]displaystyle{ 98,36~% }[/math] своей описанной окружности.

Построение

Так как [math]displaystyle{ 20 = 2^2cdot5 }[/math], правильный двадцатиугольник можно построить при помощи циркуля и линейки, или при помощи разбиения сторон правильного десятиугольника, или двойного разбиения сторон правильного пятиугольника.

Золотое сечение в правильном двадцатиугольнике

Построение правильного двадцатиугольника с заданной длиной стороны

  • При построении с заданной длиной стороны, дуга окружности с центром [math]displaystyle{ C }[/math] и радиусом [math]displaystyle{ overline{CD} }[/math], разделяет сегмент [math]displaystyle{ overline{E_{20}F} }[/math] в отношении, равном золотому сечению.
[math]displaystyle{ frac{overline{ E_{20}E_1}}{overline{E_1 F}} = frac{overline{E_{20} F}}{overline{ E_{20}E_1}} = frac{1+ sqrt{5}}{2} = Phi approx 1.618 }[/math]

Симметрия

Группы симметрий правильного двадцатиугольника. Симметричные вершины окрашены в одинаковые цвета. Голубые зеркала проведены через вершины, фиолетовые — через стороны. Порядки групп вращений даны в центре.

Симметрии правильного двадцатиугольника образуют диэдральную группу [math]displaystyle{ mathrm{D}_{20} }[/math]. В ней можно выделить пять подгрупп диэдральных симметрий ([math]displaystyle{ mathrm{D}_{10}, mathrm{D}_5, mathrm{D}_4, mathrm{D}_2 }[/math] и [math]displaystyle{ mathrm{D}_1 }[/math]), и шесть циклических подгрупп ([math]displaystyle{ mathrm{Z}_{20}, mathrm{Z}_{10}, mathrm{Z}_5, mathrm{Z}_4, mathrm{Z}_2 }[/math] и [math]displaystyle{ mathrm{Z}_1 }[/math]). Все различные подгруппы симметрий правильного двадцатиугольника могут быть графически отображены диаграммой из [math]displaystyle{ 16 }[/math] элементов.

В данной диаграмме, предложенной Джоном Конвеем, каждая подгруппа симметрии обозначена буквой и собственным порядком.[1] Вся группа симметрий названа [math]displaystyle{ mathrm{r}40 }[/math], а тривиальная подгруппа, соответствующая полному отсутствию симметрии, обозначена как [math]displaystyle{ mathrm{a}1 }[/math]. Диэдрические группы симметрии делятся на те, оси симметрий которых проходят только через вершины ([math]displaystyle{ mathrm{d} }[/math] — diagonal), только через рёбра ([math]displaystyle{ mathrm{p} }[/math] — perpendicular) или через и то, и другое (такая подгруппа обозначена буквой [math]displaystyle{ mathrm{i} }[/math]). Циклические симметрии обозначены буквой [math]displaystyle{ mathrm{g} }[/math] (англ. gyration) и своим порядком.

Группа симметрий любого неправильного двадцатиугольника образует подгруппу [math]displaystyle{ mathrm{D}_{20} }[/math]. Среди них наиболее симметричными являются фигуры, соответствующие симметриям [math]displaystyle{ mathrm{d}20 }[/math] (изогональный двадцатиугольник, построенный при помощи десяти зеркал с чередованием длинных и коротких рёбер) и [math]displaystyle{ mathrm{p}20 }[/math] (изотоксальный двадцатиугольник, в котором все стороны равны между собой, но внутренние углы при вершинах чередуются). Эти две формы двойственны[en] друг другу и каждая из них обладает половиной симметрий правильного двадцатиугольника.

Разбиения

Двадцатиугольник, разбитый на 180 ромбов

20-gon rhombic dissection-size2.svg
Правильное разбиение 		Isotoxal 20-gon rhombic dissection-size2.svg
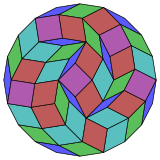
Изотоксальное разбиение

По Коксетеру, любой зоногон ([math]displaystyle{ 2m }[/math]-угольник, у которого противоположные стороны равны и параллельны друг другу) может быть разбит на [math]displaystyle{ m(m-1)/2 }[/math] параллелограммов[2]. В частности, это так для всех правильных многоугольников с чётным числом сторон — в этом случае все параллелограммы являются ромбами. Для двадцатиугольника [math]displaystyle{ m=10 }[/math], а значит, его можно разбить на [math]displaystyle{ 45 }[/math] параллелограммов: [math]displaystyle{ 5 }[/math] квадратов и [math]displaystyle{ 4 }[/math] набора ромбов — по [math]displaystyle{ 10 }[/math] в каждом. Это разбиение основано на проекции Декеракта в виде многоугольника Петри с [math]displaystyle{ 45 }[/math] гранями из [math]displaystyle{ 11520 }[/math]. Согласно данным из последовательности A006245, количество всевозможных описанных разбиений [math]displaystyle{ 20 }[/math]-угольника равно [math]displaystyle{ 18410581880 }[/math], если зеркальные и повёрнутые копии разбиения считать различными.

Изображение декеракта и примеры разбиения 20-угольника на 45 ромбов

10-cube.svg
Декеракт 		20-gon-dissection.svg 20-gon rhombic dissection2.svg 20-gon rhombic dissectionx.svg 20-gon-dissection-random.svg

Связанные многоугольники

Икосаграмма — звёздчатый многоугольник с двадцатью сторонами, имеющий символ Шлефли [math]displaystyle{ {20/n} }[/math]. Есть три правильных икосаграммы с символами Шлефли [math]displaystyle{ {20/3} }[/math], [math]displaystyle{ {20/7} }[/math] и [math]displaystyle{ {20/9} }[/math]. Есть также ещё 5 звёздчатых многоугольников с тем же относительным расположением вершин: [math]displaystyle{ 2{10} }[/math], [math]displaystyle{ 4{5} }[/math], [math]displaystyle{ 5{4} }[/math], [math]displaystyle{ 2{10/3} }[/math], [math]displaystyle{ 4{5/2} }[/math] и [math]displaystyle{ 10{2} }[/math].

n 1 2 3 4 5
Форма Выпуклый многоугольник Составной Звёздчатый многоугольник Составной
Фото Regular polygon 20.svg
[math]displaystyle{ {20/1} = {20} }[/math] 		Regular star figure 2(10,1).svg
[math]displaystyle{ {20/2} = 2{10} }[/math] 		Regular star polygon 20-3.svg
[math]displaystyle{ {20/3} }[/math] 		Regular star figure 4(5,1).svg
[math]displaystyle{ {20/4} = 4{5} }[/math] 		Regular star figure 5(4,1).svg
[math]displaystyle{ {20/5} = 5{4} }[/math]
Внутренний угол [math]displaystyle{ 162^circ }[/math] [math]displaystyle{ 144^circ }[/math] [math]displaystyle{ 126^circ }[/math] [math]displaystyle{ 108^circ }[/math] [math]displaystyle{ 90^circ }[/math]
n 6 7 8 9 10
Форма Составной Звёздчатый многоугольник Составной Звёздчатый многоугольник Составной
Фото Regular star figure 2(10,3).svg
[math]displaystyle{ {20/6} = 2{10/3} }[/math] 		Regular star polygon 20-7.svg
[math]displaystyle{ {20/7} }[/math] 		Regular star figure 4(5,2).svg
[math]displaystyle{ {20/8} = 4{5/2} }[/math] 		Regular star polygon 20-9.svg
[math]displaystyle{ {20/9} }[/math] 		Regular star figure 10(2,1).svg
[math]displaystyle{ {20/10} = 10{2} }[/math]
Внутренний угол [math]displaystyle{ 72^circ }[/math] [math]displaystyle{ 54^circ }[/math] [math]displaystyle{ 36^circ }[/math] [math]displaystyle{ 18^circ }[/math] [math]displaystyle{ 0^circ }[/math]

Более глубокие усечения правильного десятиугольника и декаграммы могут привести к изогональным (вершинно-транзитивным) промежуточным формам икосаграмм с одинаково расположенными вершинами и двумя длинами ребер.[3]

Примечания

  1. ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
  2. ↑ Коксетер, Mathematical recreations and Essays, Thirteenth edition, p.141
  3. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Источник

Как найти сумму углов выпуклых девятиугольника, двенадцатиугольника и двадцатиугольника?

Найди верный ответ на вопрос ✅ «Как найти сумму углов выпуклых девятиугольника, двенадцатиугольника и двадцатиугольника? …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Новые вопросы по геометрии

Главная » Геометрия » Как найти сумму углов выпуклых девятиугольника, двенадцатиугольника и двадцатиугольника?

Источник

Добавить комментарий