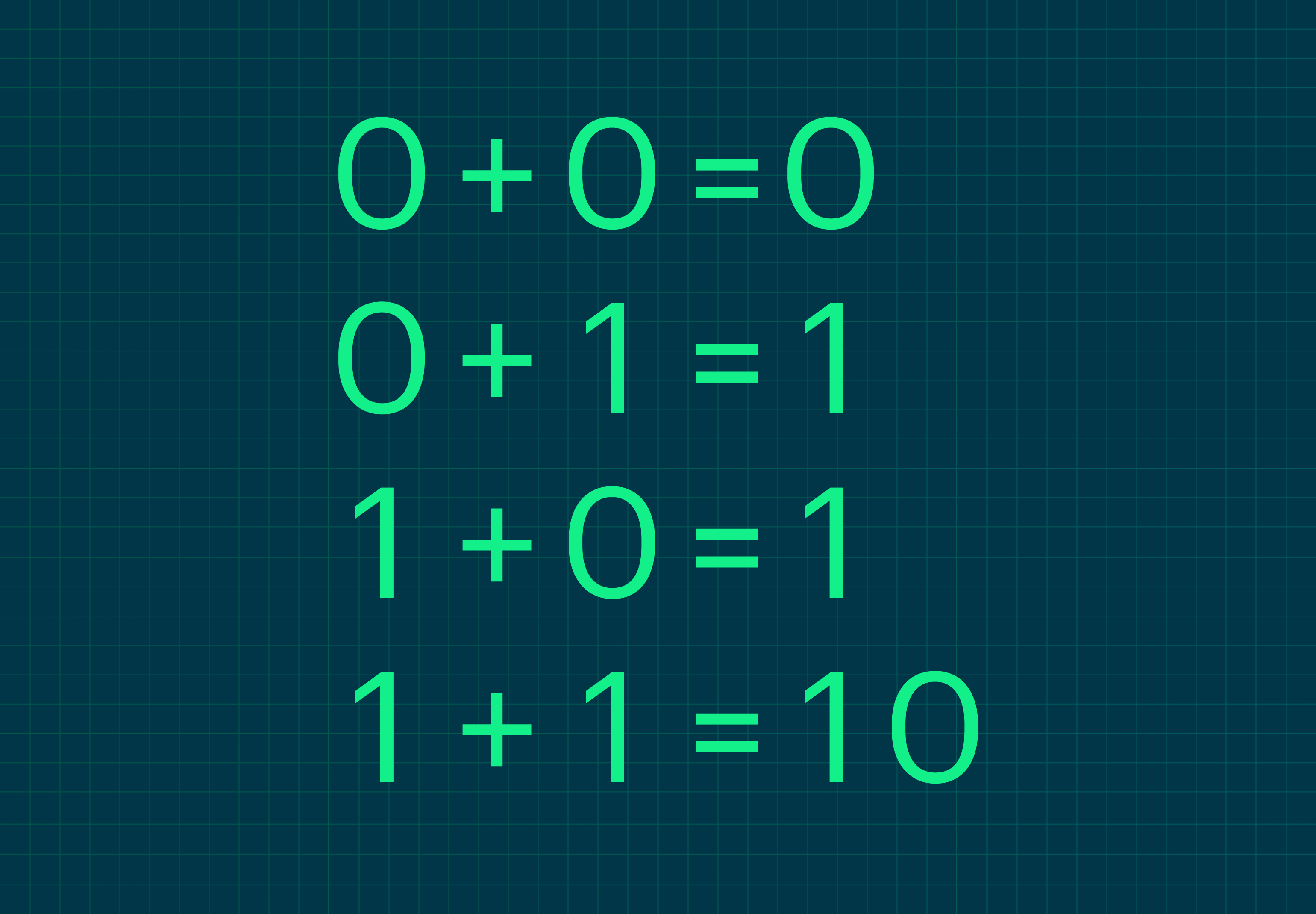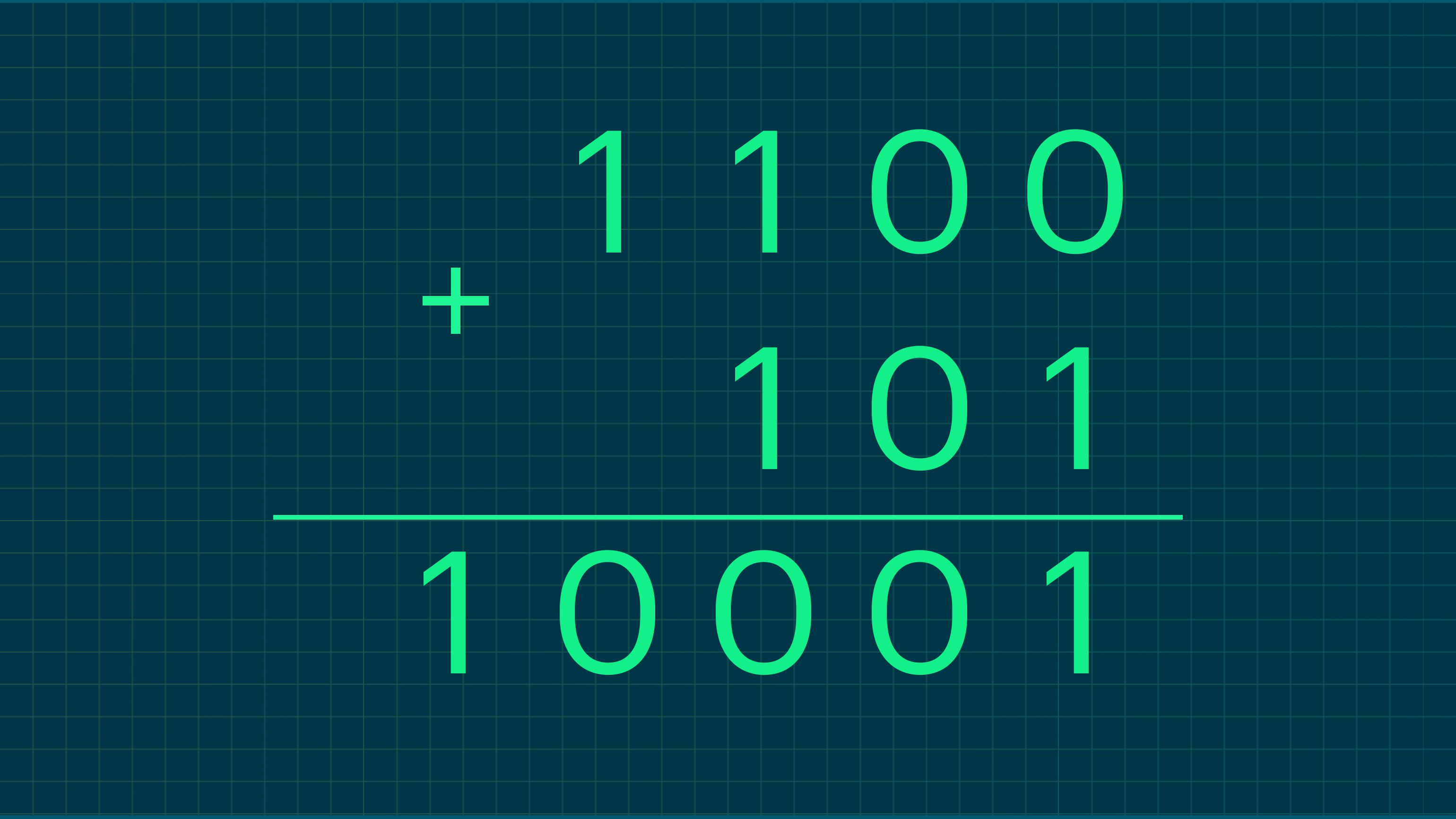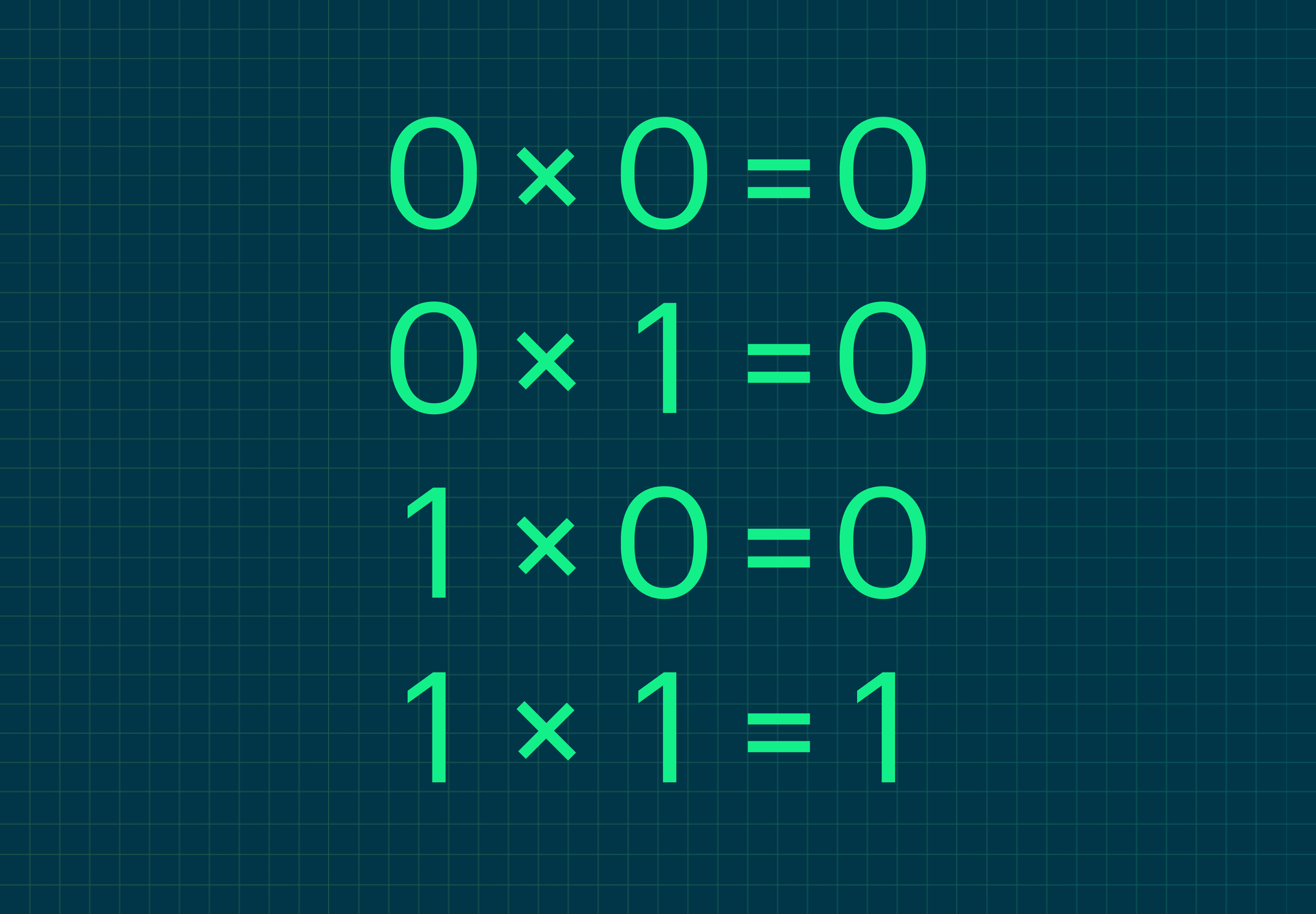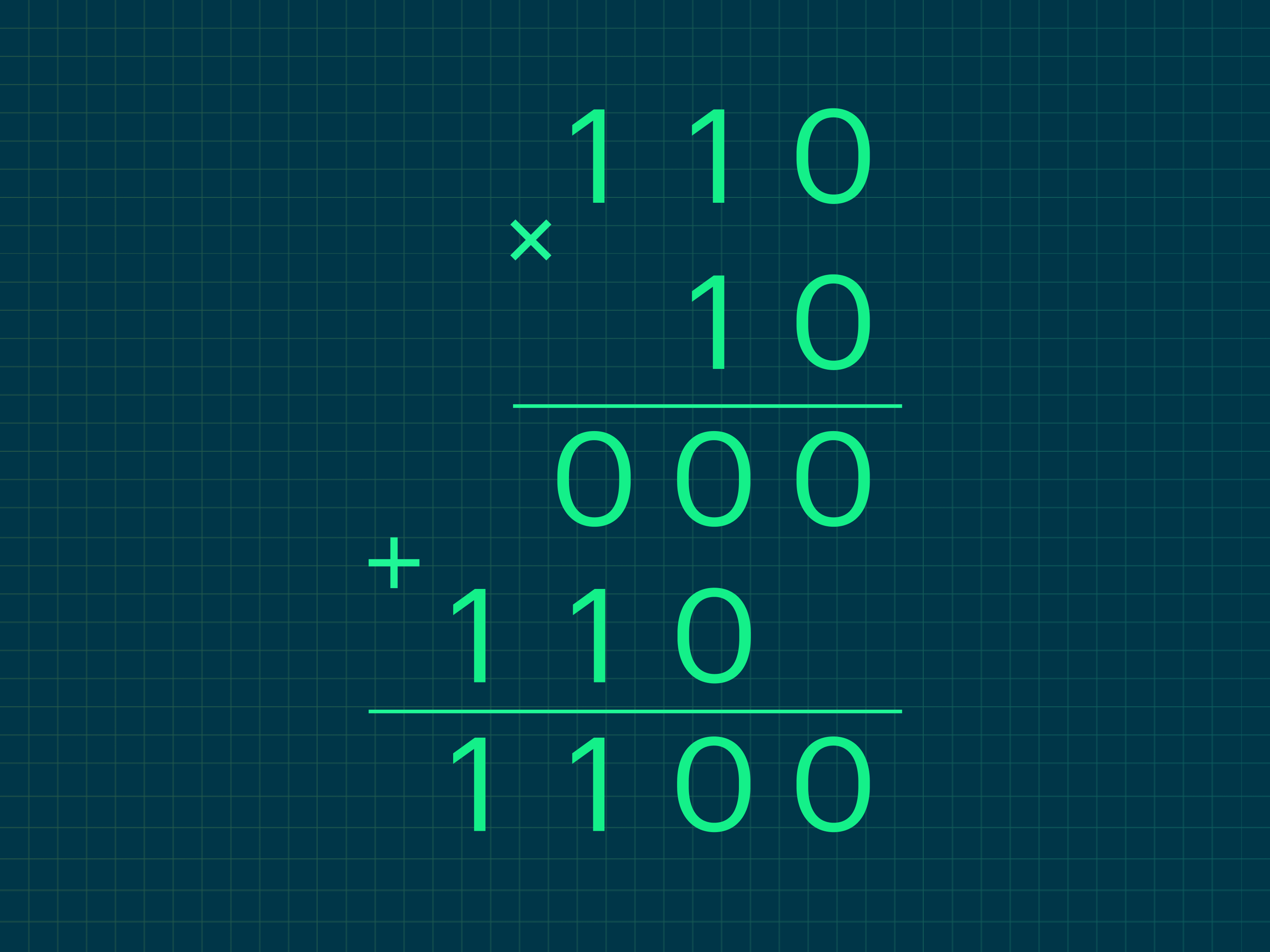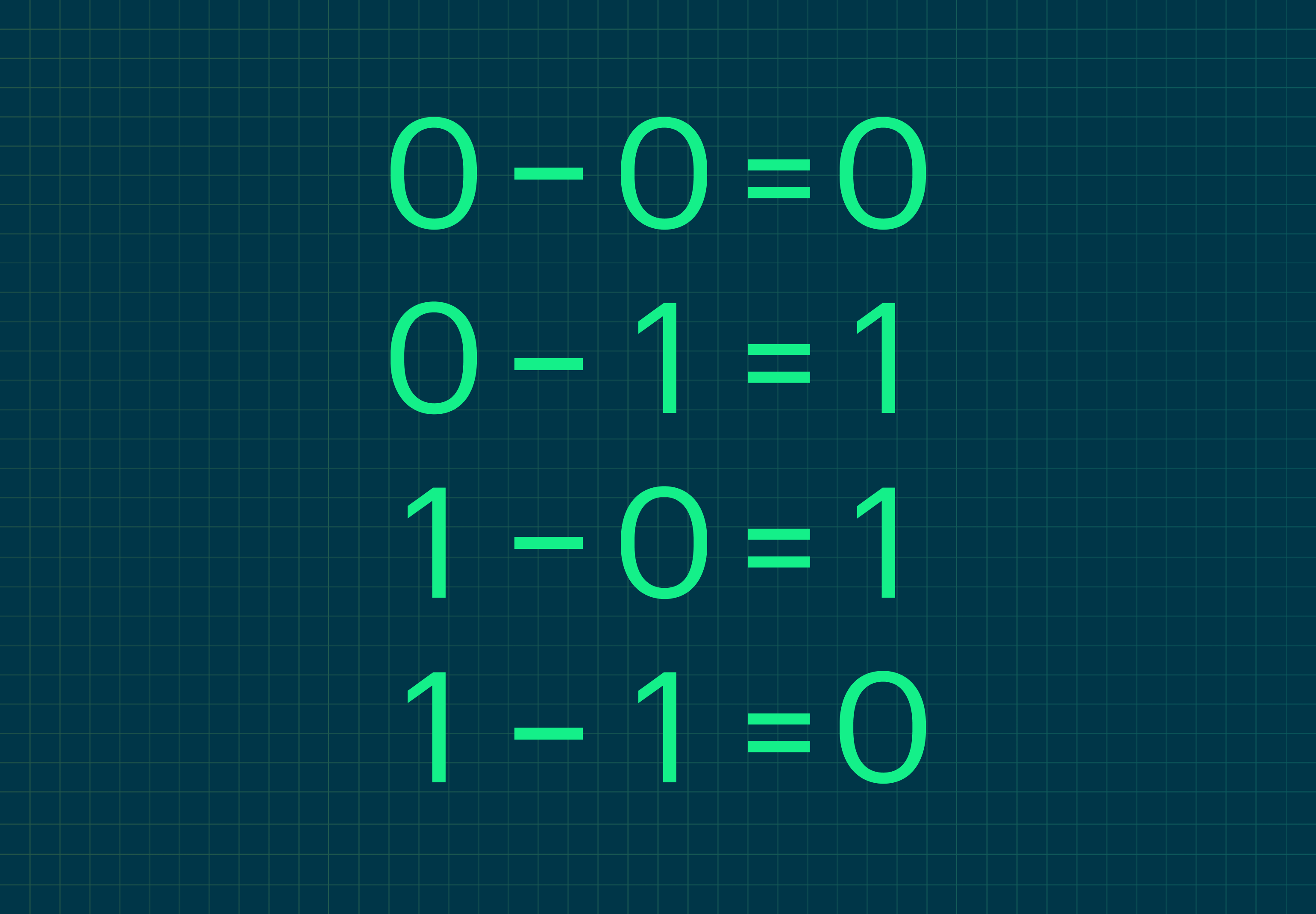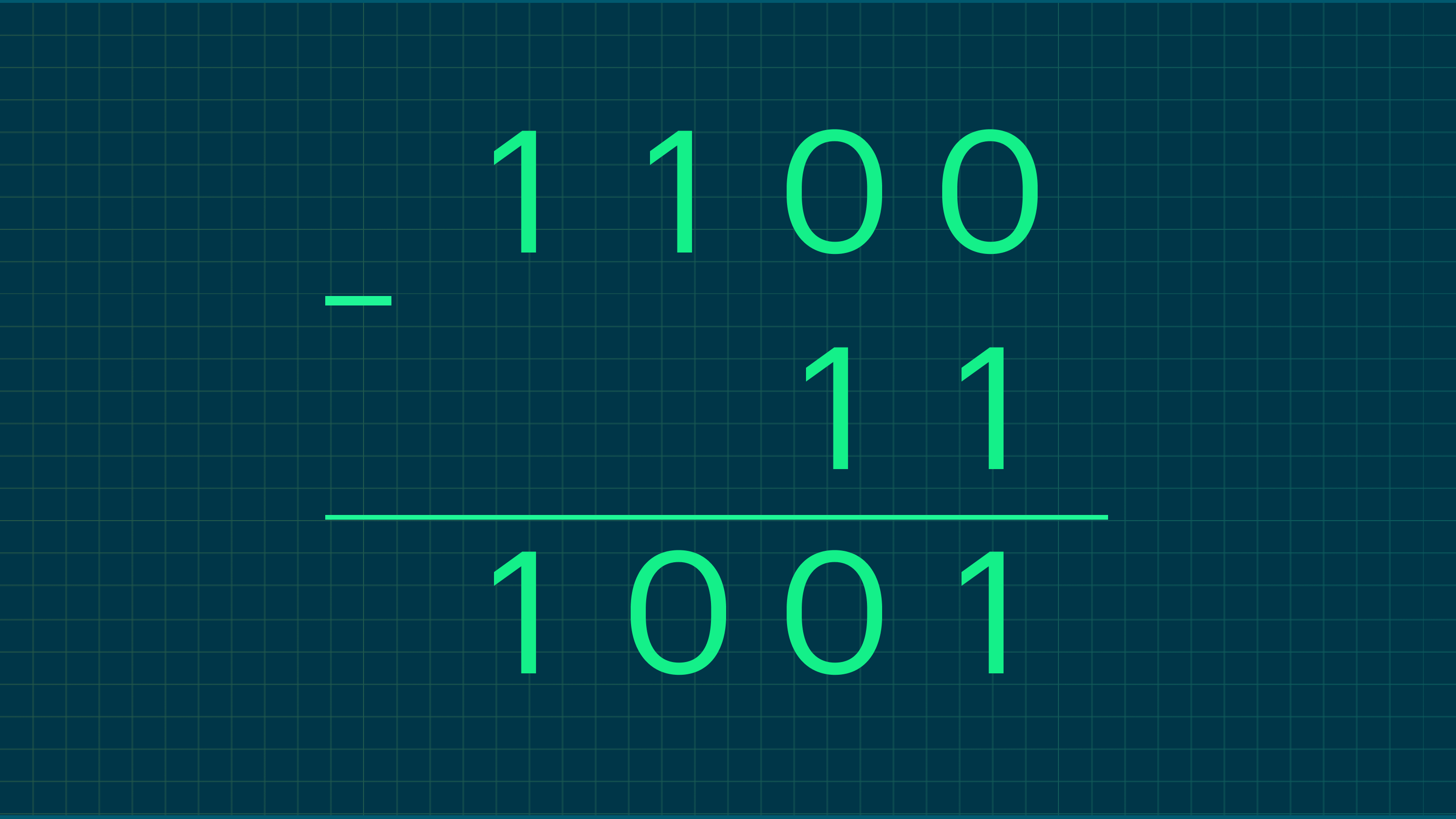Все
операции в ЭВМ выполняются в двоичной
системе счисления. Однако, человеку
удобно вводить информацию и получать
результаты вычислений в десятичной
системе счисления. Для этого используются,
так называемые, двоично-десятичные
коды. В них
один
десятичный разряд представляют четырьмя
двоичными разрядами (тетрадой). При
помощи четырех бит можно закодировать
шестнадцать различных символов (цифр).
Существует много разных систем кодирования
[10], но наиболее широко применяется код
прямого замещения – код 8–4–2–1 (это веса
двоичных разрядов влево от запятой).
Составим таблицу соответствия
двоично-десятичного кода и десятичных
цифр:
-
Двоично-десятичный
кодДесятичная
цифра8 4
2 10
0
0
0
0
0
0
0
1
1
0
0
1
0
2
0
0
1
1
3
0
1
0
0
4
0
1
0
1
5
0
1
1
0
6
0
1
1
1
7
1
0
0
0
8
1
0
0
1
9
Остальные
комбинации двоичного кода являются
лишними (запрещенными). Запишем пример
двоично-десятичного кода:
1258 = 0001 0010 0101 1000
589 = 0000
0101 1000 1001
Сложение двоично-десятичных чисел
Сложение
двоично-десятичных чисел производится
по правилам двоичной арифметики, с
учетом переносов. Пусть имеем два
десятичных числа А и В. Требуется найти
сумму С = А + В.
В
каждой тетраде выполняется сложение
трёх чисел – двух слагаемых и переноса
из предыдущего разряда, т.е. аn
+ bn
+ pn-1.
При этом
возможны такие ситуации.
1)
аn
+ bn
+ pn-1
< 10 .
А = 14 В = 23 С = А + В = 37
А
= 0001 0100
В
= 0010 0011
С
= 0011 0111
37 Ответ получился верный.
2)
аn
+ bn
+ pn-1
> 15 .
А = 47 В = 39 С = А + В = 86
А = 0100 0111
В = 0011 1001
С
= 1000
0000
80 Ответ получился неверный, так
как был перенос из младшей тетрады в
старшую. Тетрада переполняется числом
16, т.е. единица межтетрадного переноса
уносит в старшую тетраду 16 , а не 10 единиц
как в десятичной системе счисления (
шесть лишних единиц! ). Поэтому результат
необходимо скорректировать путём
добавки + 6. Выполним коррекцию
С = 1000 0000
0000
0110 – коррекция ( + 6 )
ответ
1000 0110
86 Ответ правильный.
3)
10
аn
+ bn
+ pn-1
15 А = 47 В = 36 С = А + В =83
А = 0100
0111
В = 0011
0110
С
= 0111 1101
Ответ неверный, хотя и нет
межтетрадного переноса, но имеется
запрещённая комбинация. Необходимо
вызвать искусственное переполнение
тетрады путём добавки +6. Выполним
коррекцию
С
= 0111 1101
0000
0110 – коррекция ( + 6 )
ответ
10000011
83 Теперь ответ правильный. Внимание!
Коррекция результата выполняется только
один раз, поэтому межтетрадный перенос
при коррекции не требует ещё одной
коррекции.
Таким
образом, при сложении двоично – десятичных
чисел выполняется коррекция результата
по правилу – если был межтетрадный
перенос (переполнение тетрады) или
получилась запрещённая комбинация, то
к этой тетраде добавляется + 6 (0110).
Ещё
один пример. А = 479 В = 128 С = А
+ В = 607
В
старшей тетраде коррекция 0, в средней
– +6 (запрещённая комбинация), в младшей
тетраде +6 ( был перенос ).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Данный онлайн калькулятор предназначен для сложения вычитания а также деления и умножения двоичных чисел онлайн.
| Поставить LIKE | и поделиться ссылкой |
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме
Введите два двоичных числа и выберите что вы хотите с ними сделать – сложить,вычесть, умножить или разделить
Попробуйте новый сайт: Перейти
|
1 / 1 / 0 Регистрация: 19.12.2011 Сообщений: 14 |
|
|
1 |
|
Найти сумму двух чисел в двоично-десятичной системе счисления04.07.2012, 10:59. Показов 8474. Ответов 21
Найти сумму двух чисел в двоично-десятичной системе счисления
0 |
|
1146 / 954 / 76 Регистрация: 11.10.2010 Сообщений: 6,031 |
|
|
04.07.2012, 21:43 |
2 |
|
Найти сумму двух чисел в двоично-десятичной системе счисления A+B=C
0 |
|
1 / 1 / 0 Регистрация: 19.12.2011 Сообщений: 14 |
|
|
04.07.2012, 23:15 [ТС] |
3 |
|
Я так решал не правильно было……. Там как-то по -другому надо!
0 |
|
Платежеспособный зверь 8818 / 4245 / 1618 Регистрация: 28.10.2009 Сообщений: 11,385 |
|
|
05.07.2012, 00:38 |
4 |
|
Решение
Найти сумму двух чисел в двоично-десятичной системе счисления А=0010 0101 (2-10) сумма:
5 |
|
1 / 1 / 0 Регистрация: 19.12.2011 Сообщений: 14 |
|
|
05.07.2012, 08:29 [ТС] |
5 |
|
Спс большое!
0 |
|
12 / 12 / 0 Регистрация: 23.12.2009 Сообщений: 149 |
|
|
24.08.2012, 16:26 |
6 |
|
ничего себе вы из мухи слона залепили!!!!!!!!!!!!все элементарно и просто…какие то 9е тетрады…выдумали же…
0 |
|
kazak |
|
24.08.2012, 18:50
|
|
Не по теме: proset, а теперь еще раз внимательно перечитайте задание.:)
1 |
|
12 / 12 / 0 Регистрация: 23.12.2009 Сообщений: 149 |
|
|
27.08.2012, 10:44 |
8 |
|
Не по теме: proset, а теперь еще раз внимательно перечитайте задание.:) а теперь расскажите мне,такому глупому,чем система 8421 (двоично-десятичная) отличается от обычной двоичной сс?! Я за 4 года обучения в универе по специальности АСУ еще ни одного отличия не нашел…тем более на ответ посмотрите…он такой же…так что нечего городить огороды,там где этого не нужно
0 |
|
3325 / 2590 / 313 Регистрация: 11.03.2009 Сообщений: 5,916 |
|
|
27.08.2012, 19:55 |
9 |
|
Решение
а теперь расскажите мне,такому глупому,чем система 8421 (двоично-десятичная) отличается от обычной двоичной сс?! Хотя бы тем, что в десятично-двоичном кодировании каждый десятичный разряд кодируется 4-мя битами. и 116 в десятичной системе счисления в двоично-десятичное будет выглядеть как 0001 0001 0110, в двоичной же 1110100. где же они одинаковые?
3 |
|
12 / 12 / 0 Регистрация: 23.12.2009 Сообщений: 149 |
|
|
27.08.2012, 22:07 |
10 |
|
0 |
|
3325 / 2590 / 313 Регистрация: 11.03.2009 Сообщений: 5,916 |
|
|
28.08.2012, 00:07 |
11 |
|
0 |
|
1146 / 954 / 76 Регистрация: 11.10.2010 Сообщений: 6,031 |
|
|
28.08.2012, 09:27 |
12 |
|
уважаемый proset, вы забыли что тема обсуждается в рамках школьной Информатики, поэтому ваши университетские знания немного не к месту, а то что от “перемены слагаемых сумма не меняется”, не поспоришь…
0 |
|
Платежеспособный зверь 8818 / 4245 / 1618 Регистрация: 28.10.2009 Сообщений: 11,385 |
|
|
28.08.2012, 10:52 |
13 |
|
Вот такие у нас специалисты по АСУ. Путают божий дар с яичницей. Жаль, что преподы не объяснили этому убогому что такое двоично-десятичная система, для чего она применяется и чем отличается от двоичной. Вот станет такой спец начальником – крайне утомит нормальных программистов.
1 |
|
12 / 12 / 0 Регистрация: 23.12.2009 Сообщений: 149 |
|
|
28.08.2012, 11:04 |
14 |
|
Вот такие у нас специалисты по АСУ. Путают божий дар с яичницей. Жаль, что преподы не объяснили этому убогому что такое двоично-десятичная система, для чего она применяется и чем отличается от двоичной. Вот станет такой спец начальником – крайне утомит нормальных программистов. ага-ага,я смотрю вы у нас много знаете…за убогого ответить готовы? или все ваши классные доводы, это ссылки на общественную помойку,называемую википедией,которую (вам для информации) и пишут такие же некомпетентные… p.s хотите агро,получайте…если у вас нет более наглядной аргументации,кроме слов “этому убогому”,то не пишите ничего,я даже читать не стану
0 |
|
Модератор 8804 / 6587 / 894 Регистрация: 14.02.2011 Сообщений: 23,152 |
|
|
28.08.2012, 11:42 |
15 |
|
ага-ага,я смотрю вы у нас много знаете…
B(2)=1011011 это число написано в двоичной системе 5B(16) ==91(10)
8421 (двоично-десятичная) отличается от обычной двоичной сс? наверно потому что ты привел одну тертаду
Я за 4 года обучения в универе по специальности АСУ еще ни одного отличия не нашел… плохо искал
а система 8421 это аналог обычной 2й сс вообше то это не аналог а именно двоичная(указание весов каждого разряда)
1 |
|
12 / 12 / 0 Регистрация: 23.12.2009 Сообщений: 149 |
|
|
28.08.2012, 11:58 |
16 |
|
вообше то это не аналог а именно двоичная(указание весов каждого разряда) лол что
0 |
|
Модератор 8804 / 6587 / 894 Регистрация: 14.02.2011 Сообщений: 23,152 |
|
|
28.08.2012, 12:11 |
17 |
|
лол что? да я всеми сообщениями в теме пытаюсь сдесь доказать то,что вы только что написалидо вас наконец то дошло…что это одно и тоже… ни хрена себе одно и тоже
1 |
|
12 / 12 / 0 Регистрация: 23.12.2009 Сообщений: 149 |
|
|
28.08.2012, 12:44 |
18 |
|
вообше то это не аналог а именно двоичная
ни хрена себе одно и тоже вы сами то определитесь
0 |
|
Модератор 8804 / 6587 / 894 Регистрация: 14.02.2011 Сообщений: 23,152 |
|
|
28.08.2012, 12:48 |
19 |
|
вы сами то определитесь в чем???
0 |
|
12 / 12 / 0 Регистрация: 23.12.2009 Сообщений: 149 |
|
|
28.08.2012, 12:54 |
20 |
|
в чем??? ну вот))вы опять процитировали мою мысль)и даже осознали это
0 |
#статьи
- 27 фев 2023
-
0
Двоичная арифметика: сложение, умножение, вычитание, деление бинарных чисел
Учимся складывать, вычитать, умножать и делить двоичные числа — работаем с фундаментальными законами современной цифровой электроники.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Мы привыкли считать всё в десятичной системе, потому что у нас 10 пальцев — и это удобно. Но если бы у нас было больше пальцев, например 12, то система могла бы быть двенадцатиричной и мы бы воспринимали её как обычную.
Когда дело доходит до двоичной системы счисления, сложно вот так сразу переключиться на её арифметику — хотя, казалось бы, принципы такие же, как для десятичной. Ведь там есть все привычные операции: сложение, вычитание, умножение, деление. Единственное отличие: в двоичных числах используются всего две цифры — ноль и единица.
Давайте избавимся от страха и наконец узнаем, как проводить знакомые нам математические операции в двоичной системе.
Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд.
В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.
Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).
Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:
Но лучше разобраться на примерах.
Пример 1. Давайте сложим 1100 и 101.
Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:
- Первый: 0 + 1 = 1.
- Второй: 0 + 0 = 0.
- Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.
Пример 2. Сложим 1111 и 111.
Теперь поразрядно:
- Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
- Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1.
Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.
Ответ
1101 + 1011 = 11000.
Умножение в двоичной системе, как в десятичной, основано на сложении — и умении считать в столбик.
Сведём в таблицу правила умножения двоичных чисел:
Давайте теперь посмотрим на реальных примерах, как правильно умножать двоичные числа.
Пример 1. Умножим 110 на 10.
Здесь мы воспользуемся привычным школьным «столбиком»: сначала умножаем верхнее число, 110, на 0, затем на 1, а потом складываем полученные два и получаем результат.
По сути, если мы умножаем число на ноль, то оно превращается в ноль, а если на единицу — остаётся неизменным, но сдвигается на число разрядов, равное номеру разряда этой единицы, как в обычном умножении:
- 110 × 0 = 000;
- 110 × 1 = 110.
Сдвигаем 110 на один разряд влево и складываем результаты промежуточных умножений:
- 000 + 1100 = 1100.
Мы получили 1100, потому что сместили результат умножения 110 × 1 на один разряд влево, а затем добавили один 0 справа — как в обычном умножении.
Пример 2. Давайте теперь умножим 101 на 101.
Не пугайтесь, что у нас получилось три числа, которые нужно сложить: правила остаются теми же. Ещё можно приписывать дополнительные нули туда, где находится пустое пространство — это поможет не запутаться.
Разберём пошагово:
- 101 × 1 = 101;
- 101 × 0 = 000;
- 101 × 1 = 101.
Снова сдвигаем влево промежуточные результаты и складываем:
- 101 + 0000 + 10100 = 11001.
Попробуйте сами умножить 1101 на 111.
Ответ
1011011.
Правила двоичного вычитания тоже ничем не отличаются от десятичного. Мы также вычитаем поразрядно и, если нужно, занимаем единицу из старшего разряда.
Таблица вычитания выглядит так:
Заметьте, что 0 − 1 = 1. Это всё потому, что мы занимаем единицу из старшего разряда и получаем 10, или 2 в десятичной системе, а если вычесть из 10 число 1, получим 1 (ведь 2 − 1 = 1).
Перейдём к примерам, чтобы понять, как вычитать одно число из другого.
Пример 1. Вычтем из 1100 число 11.
Разберём подробнее поразрядно:
- Первый: 0 − 1 = 1 — занимаем единицу из старшего разряда.
- Второй: 1 − 1 = 0 — так как отсюда заняли единицу, но у нас её не было, мы взяли её из следующего разряда и вычли единицу из этого.
- Третий: 0 − 0 = 0 — из этого разряда единица ушла в первый.
- Четвёртый: 1 − 0 = 1 — здесь всё нормально.
Всё то же знакомое нам вычитание.
Пример 2. Вычтем из 1011 число 101.
Тот же алгоритм по разрядам:
- Первый: 1 − 1 = 0.
- Второй: 1 − 0 = 1.
- Третий: 0 − 1 = 1 — заняли единицу из следующего разряда.
- Четвёртый: 0 − 0 = 0 — отдали единицу в предыдущий разряд.
Кажется, что всё несложно. Попробуйте теперь сами вычесть из 11010 число 1111.
Ответ
1011.
Вы удивитесь, но правила деления двоичных чисел похожи на деление десятичных. Рисуем привычный «столбик», умножаем, вычитаем, получаем результат.
Таблицы тут нет, потому что она бессмысленна — давайте сразу на примерах разбирать, как делить двоичные числа.
Пример 1. Поделить 1100 на 10.
У нас есть только два варианта: умножить делитель на 1 или на 0. Поэтому алгоритм будет таким:
- Смотрим на делимое, видим, что первые две его цифры — 11. Умножаем делитель на 1 и вычитаем из 11 число 10.
- Получили 1, дописываем справа следующую по порядку цифру — 0. Теперь 10 равно делителю, значит, тоже умножаем его на 1 и вычитаем.
- Получаем 0. Но у нас ещё остался один 0 у делимого — дописываем его справа от полученного 0.
- Число 0 меньше, чем 10, поэтому умножаем делитель на 0. Получаем конечный ответ — 110.
Пример 2. Поделить 10010 на 110.
Пошаговый алгоритм:
- Первые три числа делимого меньше, чем делитель — значит, умножаем делитель на 0 и вычитаем. Получаем 100.
- Дописываем 1 справа от 100, видим, что 1001 больше, чем 110, поэтому умножаем делитель на 1 и вычитаем его из 1001. Получаем 11.
- Дописываем 0 справа. Полученное 110 равно делителю, поэтому тоже умножаем его на 1, получаем конечный результат.
Попробуйте сами теперь поделить 10100 на 100.
Ответ
101.
Двоичная арифметика во многом похожа на десятичную: мы так же можем складывать, вычитать, делить и умножать числа столбиком. Правда, в двоичной системе всего две цифры: 0 и 1 — поэтому привычные математические операции в ней могут показаться немного странными. К счастью, в основе двоичной арифметики лежат простые принципы, которые нужно запомнить.

Научитесь: Профессия Python-разработчик
Узнать больше
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.
Таблица сложения, вычитания и умножения для двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 — 0 = 0 | 0 ∙ 0 = 0 |
| 0 + 1= 1 | 1 — 0 = 1 | 0 ∙ 1 = 0 |
| 1 + 0 = 1 | 1 — 1 = 0 | 1 ∙ 0 = 0 |
| 1 + 1 = 10 | 10 — 1 = 1 | 1 ∙ 1 = 1 |
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Пример: 1011,12 + 1010,112
Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,12 + 1112 + 101,12
При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 1002. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 1012. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Вычитание двоичных чисел
В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,012 — 1001,12
Умножение и деление двоичных чисел
Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 1011110112 в десятичную систему счисления.
Поскольку 1010 = 10102, запишем
Полученные остатки, 10012 = 910, =1112 = 710, 112 = 310. Искомое число 1011110112 = 37910.
Назад: Представление данных и архитектура ЭВМ



 Сообщение было отмечено как решение
Сообщение было отмечено как решение
 вы про 8421 что-нибудь слышали вообще? любое число при переводе в 2ю сс и двоично-десятичную сс будет одинаково…хотя чего это я…даже на примере в данной теме это наглядно видно…
вы про 8421 что-нибудь слышали вообще? любое число при переводе в 2ю сс и двоично-десятичную сс будет одинаково…хотя чего это я…даже на примере в данной теме это наглядно видно…
 я тебе показал отличия
я тебе показал отличия ? да я всеми сообщениями в теме пытаюсь сдесь доказать то,что вы только что написали
? да я всеми сообщениями в теме пытаюсь сдесь доказать то,что вы только что написали до вас наконец то дошло…что это одно и тоже…вы бы перечитали,то что я написал…
до вас наконец то дошло…что это одно и тоже…вы бы перечитали,то что я написал…