Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, – это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел

В общем виде вычитание можно записать так: a – b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Содержание:
- Определение суммы чисел
- Свойства суммы чисел
Определение суммы чисел
Суммой $s$ (лат. summa – итог, общее количество) чисел $a_{1}, a_{2}, dots, a_{n}$ называется результат
суммирования этих чисел: $s=a_{1}+a_{2}+ldots+a_{n}$ . В частности, если складывается два числа $a$ и $b$, то
Пример
Задание. Найти сумму чисел:
1) $12$ и $15$ 2) $1,1 ; 2,2 ; 3,3$ и $4,4$
Ответ.
$12+15=27$
$1,1+2,2+3,3+4,4=11$
Свойства суммы чисел
- Коммутативность: $n+m=m+n$
-
Ассоциативность: $(n+m)+k=n+(m+k)$
На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.
-
Дистрибутивность по отношению к умножению
$$(n+m) cdot k=n cdot k+m cdot k$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму чисел удобным способом:
1) $15+17+13$ ; 2) $34+22+16+18$
Решение. По свойствам сложения имеем
$$15+17+13 =15+(17+13)=15+30=45 $$
$$34+22+16+18 =(34+16)+(22+18)=50+40=90 $$
Ответ. 1) $15+17+13=45$
2) $34+22+16+18=90$
При сложении больших чисел или
десятичных дробей используется сложение в столбик.
Пример
Задание. Найти сумму чисел удобным способом:
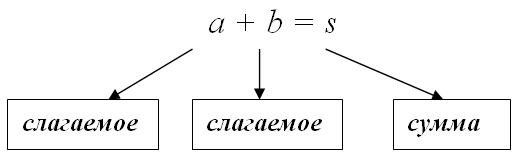
1) $1562+13827$ ; 2) $34,71+356,161$
Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом.
В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем
числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном
столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:
Ответ. 1) $1562+13827=15389$
2) $34,71+356,161=390,871$
Сложение рациональных дробей производится по правилу
$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$
Пример
Задание. Найти сумму чисел:
1) $frac{1}{4}+frac{1}{6}$ ; 2) $frac{2}{3}+1 frac{1}{2}$
Решение. Вычислим первую сумму используя правило сложения рациональных чисел
$$frac{1}{4}+frac{1}{6}=frac{1 cdot 6+1 cdot 4}{4 cdot 6}=frac{6+4}{24}=frac{10}{24}$$
Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим
$$frac{1}{4}+frac{1}{6}=frac{5}{12}$$
Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого
умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим
правило сложение рациональных дробей
$$frac{2}{3}+1 frac{1}{2}=frac{2}{3}+frac{3}{2}=frac{2 cdot 2+3 cdot 3}{3 cdot 2}=frac{4+9}{6}=frac{13}{6}$$
Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком.
Полученное частное запишем в целую часть, а остаток от деления в числитель.
$$frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$$
Ответ. 1) $frac{1}{4}+frac{1}{6}=frac{5}{12}$ ;
2) $frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$
Читать дальше: что такое произведение чисел.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 декабря 2021 года; проверки требуют 9 правок.
У этого термина существуют и другие значения, см. сумма.
Су́мма (лат. summa — итог, общее количество) в математике — результат применения операции сложения величин (чисел, функций, векторов, матриц и т. д.), либо результат последовательного выполнения нескольких операций сложения (суммирования). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:
В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы объединяемых множеств, взятые без повторений.
Также сложение (нахождение суммы) может быть определено для более сложных алгебраических структур (сумма групп, сумма линейных пространств, сумма идеалов, и другие примеры). В теории категорий определяется понятие суммы объектов.
Сумма натуральных чисел[править | править код]
Пусть в множестве 









Алгебраическая сумма[править | править код]
Сумму математически обозначают заглавной греческой буквой Σ (сигма).
где: i — индекс суммирования; ai — переменная, обозначающая каждый член в серии; m — нижняя граница суммирования, n — верхняя граница суммирования. Обозначение «i = m» под символом суммирования означает, что начальное (стартовое) значение индекса i эквивалентно m. Из этой записи следует, что индекс i инкрементируется на 1 в каждом члене выражения и остановится, когда i = n.[1]
В программировании данной процедуре соответствует цикл for.
- Примеры записи
Границы могут опускаться из записи, если они ясны из контекста:
Итератор может быть выражением — тогда переменная оформляется со скобками как функция «


Сумма 


Сумма 


Под знаком итеративного суммирования может использоваться несколько индексов, например:
причём набор из нескольких индексов можно сократить в виде так называемого мультииндекса.
Бесконечная сумма[править | править код]
В математическом анализе определяется понятие ряда — суммы бесконечного числа слагаемых.
Примеры последовательных сумм[править | править код]
1. Сумма арифметической прогрессии:
2. Сумма геометрической прогрессии:
3.
4. 
Доказательство
5. 
6. 
-
-
- Например, при
получается
, а это последовательность равенств следующего вида:
- Например, при
-
Неопределённая сумма[править | править код]
Неопределённой суммой 



что 
«Дискретная» формула Ньютона — Лейбница[править | править код]
Если найдена «производная» 

Этимология[править | править код]
Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, а также появляется глагол «суммировать» (1489 год).
Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.
Специальный символ для обозначения суммы (Σ) первым ввёл Леонард Эйлер в 1755 году, его поддержал Лагранж, однако долгое время с этим символом конкурировал знак S. Окончательно обозначение Σ для суммы утвердили уже в XVIII веке Фурье и Якоби[2].
Кодировка[править | править код]
В Юникоде есть символ суммы U+2211 ∑ n-ary summation (HTML ∑ • ∑).
См. также[править | править код]
- Сложение
- Произведение
Примечания[править | править код]
- ↑ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren. Chapter 2: Sums // Concrete Mathematics: A Foundation for Computer Science (2nd Edition) (англ.). — Addison-Wesley Professional, 1994. — ISBN 978-0201558029. (недоступная ссылка)
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 175. — 248 с. — ISBN 978-5-382-00839-4.
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — 7-е. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
Содержание
- Сумма и разность чисел
- Что такое сумма, и как ее найти
- Как найти разность чисел
- Сложение
- Как называются числа при сложении?
- Как найти неизвестное слагаемое
- Проверка сложения
- Перестановка слагаемых
- Сочетательный закон сложения
- Что такое сумма чисел?
- Ответ или решение 2
- Слагаемые как элементы суммы чисел
- Правила свойства суммы чисел
- Примеры суммы чисел и наиболее удобный способ сложения
- Свойства сложения и вычитания
- Свойства сложения
- Свойства вычитания
- Примеры использования свойств сложения и вычитания
- Числа. Сложение чисел.
- Свойства суммы чисел.
- Сложение отрицательных чисел (чисел с разными знаками). Правила.
Сумма и разность чисел
Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел

В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Источник
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 — 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 — первое слагаемое
2 — второе слагаемое
2 + 3 = 5
2 — первое слагаемое
3 — второе слагаемое
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = . (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
37 + 30 = 67, значит,
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Источник
Что такое сумма чисел?
Ответ или решение 2
Слагаемые как элементы суммы чисел
Сумма чисел это результат, который получается в результате сложения двух или нескольких чисел. Простыми словами, это определённый результат, который получит человек, в случае если приплюсует, то есть сложит числа вместе.
Правила свойства суммы чисел
Существуют так же правила, которые следует запомнить для лучшего усвоения и запоминания темы:
- От перемены мест слагаемых сумма не меняется (a + b = b + a). Например, как 5 + 4 будет равно 9, так и 4 + 5 = 9.
- c + (a + b) = b + (c + a). Иными словами, 4 + (5 + 3) = 3 + (4 + 5)
- (a + b) * c = a* c + b * c. Иными словами, мы раскрываем скобки умножая по очереди сначала одно число в скобке, потом другое на число, стоящее за этой скобкой и складываем их между собой. Например, (5 + 4) * 2 = 5 * 2 + 4 * 2
Примеры суммы чисел и наиболее удобный способ сложения
Для того, чтобы лучше уяснить данную тему, предлагаю привести примеры суммы чисел и решить их:
- 7 + 3 = 10. 7 и 3 слагаемые, а 10 это сумма чисел, которая получилась у нас в результате сложения;
- 10 + 2 = 12. 10 и 2 это слагаемые, а 12 это сумма чисел.
Бывают такие случаи, когда пример сложения длинный, для таких случаев существует более удобный и быстрый способ нахождения суммы чисел: Найти числа, которые в сумме друг с другом дадут десятки. Например: 13 + 7 + 7 + 13 + 20. Решение в данном случае следует провести следующим образом: (13 + 7) + (7 + 13) + 20 = 20 + 20 + 20 = 60. Сумма чисел в данном случае 60.
Для решения данного задания, вспомним, что сумму мы получаем в результате сложения чисел.
Источник
Свойства сложения и вычитания
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое,
- 5 — второе слагаемое,
- 7 — это сумма.
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
- Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
a + b = b + a - Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c) - Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
При этом саму запись (9 — 4) тоже можно назвать разностью.

- Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
a — 0 = a
Если из числа вычесть само число, то получится нуль.
a — a = 0 - Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
a — (b + c) = a — b — c - Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) — c = (a — c) + b (если a > c или а = с)
(a + b) — c = (b — c) + a (если b > c или b = с)
Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:
Пример 1
Вычислить сумму слагаемых с использованием разных свойств:
а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15
б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22
в) 30 + 0 + 13 = 30 + 13 = 43
Пример 2
Применить разные свойства при вычислении разности:
а) 25 — 0 — 2 = 25 — 2 = 23
б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13
Пример 3
Найти значение выражения удобным способом:
а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32
б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16
Источник
Числа. Сложение чисел.
Сумма — итог складывания величин (чисел, функций, векторов, матриц и т.д.). Свойства для всякого случая – это свойства коммутативности, ассоциативности и дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение существует), т.е. выполнение соотношений:
В теории множеств суммой (или объединением) множеств является множество, в котором элементы – это все элементы слагаемых множеств, которое берутся без повторов.
Суммой s чисел 

Свойства суммы чисел.
- Коммутативность:
- Ассоциативность:
Основываясь на выше приведенных свойствах сложения натуральных чисел можно сделать вывод, что от перестановки мест слагаемых сумма не меняется.
- Дистрибутивность по отношению к умножению:
- Для сложения больших чисел (двузначных и многозначных чисел) либо десятичных дробей удобней пользоваться сложением в столбик.
- Сложение рациональных дробей производится по правилу:
Сложение отрицательных чисел (чисел с разными знаками). Правила.
Для сложения двух натуральных чисел чисел с разными знаками, нужно:
1) из модуля числа , который больше, меньший вычесть модуль;
2) поставить перед результатом знак того слагаемого, у которого модуль больше.
Источник
- Главная
- Справочники
- Справочник по математике для начальной школы
- Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
Подскажи ему.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
Рассмотрите рисунок.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Рассмотри рисунок.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
8 + 4 = 12
12 – 4 = 8
12 – 8 = 4
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 – 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 – первое слагаемое
2 – второе слагаемое
5 сумма
2 + 3 = 5
2 – первое слагаемое
3 – второе слагаемое
5 – сумма
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = …. (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
29 + 1 = 30
37 + 30 = 67, значит,
(37 + 29) + 1 = 67
Вывод: два соседних слагаемых можно заменить их суммой.
Советуем посмотреть:
Табличное сложение
Письменное сложение в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 127,
Моро, Волкова, Степанова, Учебник, часть 1
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 26,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 47,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 104,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 109,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 49. Урок 30,
Петерсон, Учебник, часть 1
Страница 29. Урок 15,
Петерсон, Учебник, часть 2
Страница 53. Урок 27,
Петерсон, Учебник, часть 2
2 класс
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 6. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 62,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 31. Урок 16,
Петерсон, Учебник, часть 1
Страница 39. Урок 20,
Петерсон, Учебник, часть 1
Страница 37. Урок 14,
Петерсон, Учебник, часть 2
Страница 38. Урок 15,
Петерсон, Учебник, часть 2
3 класс
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 97,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 4. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 79. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 23. Урок 10,
Петерсон, Учебник, часть 2
Страница 85. Урок 37,
Петерсон, Учебник, часть 2
Страница 32. Урок 15,
Петерсон, Учебник, часть 3
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 9. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 43. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 90. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 219,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
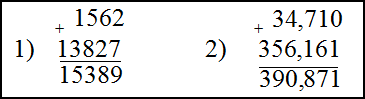














![sum limits _{{k=1}}^{n}k^{3}=left[{frac {n(n+1)}{2}}right]^{2}=left(sum limits _{{k=1}}^{n}kright)^{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c341ce59623204355f8577a50b0e02b49e30240d)