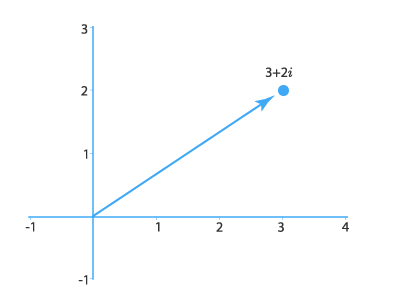Как найти сумму двух комплексных чисел - Сайт, где вы сможете решить свои вопросы

Содержание:

Сложение комплексных чисел
Вычитание комплексных чисел

Сложение комплексных чисел

Определение

Суммой двух комплексных чисел $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$ называется
комплексное число
$z$, которое равно

$z=left(a_{1}+a_{2}right)+left(b_{1}+b_{2}right) i$

То есть суммой двух комплексных чисел есть комплексное число,
действительная и мнимая части
которого есть суммой действительных и мнимых частей чисел-слагаемых соответственно.

Пример

Задание. Найти сумму
$z_{1}+z_{2}$, если
$z_{1}=5-6 i$,
$z_{2}=-3+2 i$ .

Решение. Искомая сумма равна

$z_{1}+z_{2}=5-6 i+(-3+2 i)=(5+(-3))+(-6+2) i=2-4 i$

Ответ. $z_{1}+z_{2}=2-4 i$

Вычитание комплексных чисел

Определение

Разностью двух комплексных чисел $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$ называется комплексное число
$z=z_{1}-z_{2}$, действительная и мнимая части
которого есть разностью действительных и мнимых частей чисел
$z_{1}$ и
$z_{2}$ соответственно:

$z=left(a_{1}-a_{2}right)+left(b_{1}-b_{2}right) i$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти разность
$z_{1}-z_{2}$, если
$z_{1}=5-6 i$,
$z_{2}=-3+2 i$ .

Решение. Действительная часть искомого комплексного числа равна разности действительных частей чисел
$z_{1}$ и
$z_{2}$ , а мнимая – мнимых частей этих чисел, то есть

$z_{1}-z_{2}=5-6 i-(-3+2 i)=(5-(-3))+(-6-2) i=8-8 i$

Ответ. $z_{1}-z_{2}=8-8 i$

Читать дальше: умножение комплексных чисел.

Источник

Найти сумму или разность двух комплексных чисел — такие задачи часто возникают при изучении высшей математики. В этой статье подробно рассматриваются операции сложения и вычитания комплексных чисел в алгебраической форме.

Если вам необходимо вспомнить, что же такое комплексные числа, то обратитесь к этой статье.

Сложение комплексных чисел

Чтобы сложить два комплексных числа, мы складываем каждую часть (действительную и мнимую) отдельно и получаем формулу сложения комплексных чисел:

( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i

Пример сложения комплексных чисел:

( 4 + 6 i ) + (8 — 3 i) = ( 4 + 8 ) + ( 6 — 3 ) i = 12 + 3 i

Вычитание комплексных чисел

Чтобы вычесть одно комплексное число из другого, для этого нужно также вычесть каждую часть отдельно:

( a + b i ) — ( c + d i ) = ( a — c ) + ( b — d ) i

Пример вычитания комплексных чисел:

( 2 + 11 i ) — ( 9 + 6 i ) = ( 2 — 9 ) + ( 11 — 6 ) i = -7 + 5 i

Еще примеры:

5 — ( 3 + 2 i) = ( 5 + 0 i ) — ( 3 + 2 i ) = ( 5 — 3 ) + ( 0 — 2 ) i = 2 — 2 i

( 7 — 8 i ) + 4 i = ( 7 — 8 i ) + ( 0 + 4 i ) = ( 7 + 0 ) + ( — 8 + 4 ) i = 7 — 4 i

Следующим этапом вы можете освоить операцию умножения комплексных чисел, перейдя по этой ссылке.

Источник

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.

Определение 1

Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством

[z_{1} +z_{2} =(a_{1} +b_{1} i)+(a_{2} +b_{2} i)=(a_{1} +a_{2} )+(b_{1} +b_{2} )cdot i.]

Другими словами, суммой двух заданных комплексных чисел является комплексное число, действительная и мнимая части которого определяется как сумма соответственно действительных и мнимых частей исходных слагаемых.

Примечание 1

Сумму любого количества заданных комплексных чисел можно найти путем суммирования действительных частей и суммирования мнимых частей слагаемых.

Примечание 2

Для операции суммы комплексных чисел справедливо следующее правило:

(от перестановки слагаемых сумма не меняется).

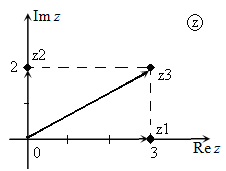
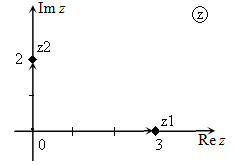
Иллюстрация примера сложения комплексных чисел с использованием комплексной плоскости приведена на рис.1-2.

Рис. 1

Рис. 2

Пример 1

Найти сумму $z_{1} +z_{2} $ для комплексных чисел:

1) $z_{1} =3+2i$ и $z_{2} =1-2i$; 2) $z_{1} =3$ и $z_{2} =1+5i$; 3) $z_{1} =3+9i$ и $z_{2} =-7i$.

Решение:

Для сложения комплексных чисел воспользуемся определением и получим:

1) $z_{1} +z_{2} =(3+2i)+(1-2i)=(3+1)+(2-2)i=4+0cdot i=4$

2) $z_{1} +z_{2} =(3+0cdot i)+(1+5i)=(3+1)+(0+5)i=4+5i$

3) $z_{1} +z_{2} =(3+9i)+(0-7i)=(3+0)+(9-7)i=3+2i$

«Сложение и вычитание комплексных чисел» 👇

Пример 2

Найти модуль суммы $|z_{1} +z_{2} |$ двух заданных комплексных чисел:

1) $z_{1} =1+2i$ и $z_{2} =1-5i$; 2) $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$; 3) $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$.

Решение:

Для сложения комплексных чисел воспользуемся определением. Для вычисления модуля комплексного числа воспользуемся формулой:

[|z|=sqrt{a^{2} +b^{2} } .]

1) Для чисел $z_{1} =1+2i$ и $z_{2} =1-5i$ получим:

[z_{1} +z_{2} =(1+2i)+(1-5i)=(1+1)+(2-5)i=2+(-3)cdot i]

[|z_{1} +z_{2} |=sqrt{2^{2} +(-3)^{2} } =sqrt{4+9} =sqrt{13} .]

2) Для чисел $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$ получим:

[z_{1} +z_{2} =(sqrt{3} +0cdot i)+(0+sqrt{5} cdot i)=(sqrt{3} +0)+(0+sqrt{5} )i=sqrt{3} +sqrt{5} cdot i]

[|z_{1} +z_{2} |=sqrt{(sqrt{3} )^{2} +(sqrt{5} )^{2} } =sqrt{3+5} =sqrt{8} =2sqrt{2} .]

3) Для чисел $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$ получим:

[z_{1} +z_{2} =(sqrt{3} +9i)+(0-7i)=(sqrt{3} +0)+(9-7)i=sqrt{3} +2cdot i]

[|z_{1} +z_{2} |=sqrt{(sqrt{3} )^{2} +2^{2} } =sqrt{3+4} =sqrt{7} .]

Определение 2

Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством

[z_{1} -z_{2} =(a_{1} +b_{1} i)-(a_{2} +b_{2} i)=(a_{1} -a_{2} )+(b_{1} -b_{2} )cdot i.]

Примечание 4

Модуль разности двух заданных комплексных чисел равен расстоянию между точками, которые изображают эти числа на комплексной плоскости:

[|z_{1} -z_{2} |=sqrt{(a_{1} -a_{2} )^{2} +(b_{1} -b_{2} )^{2} } .]

Пример 3

Найти разность $z_{1} -z_{2} $ для комплексных чисел:

1) $z_{1} =3+2i$ и $z_{2} =1-2i$; 2) $z_{1} =3$ и $z_{2} =1+5i$; 3) $z_{1} =3+9i$ и $z_{2} =-7i$.

Решение:

Для нахождения разности комплексных чисел воспользуемся определением и получим:

1) $z_{1} -z_{2} =(3+2i)-(1-2i)=(3-1)+(2-(-2))i=2+4i$

2) $z_{1} -z_{2} =(3+0cdot i)-(1+5i)=(3-1)+(0-5)i=2-5i$

3) $z_{1} -z_{2} =(3+9i)-(0-7i)=(3-0)+(9-(-7))i=3+16i$

Пример 4

Найти модуль разности двух заданных комплексных чисел:

1) $z_{1} =1+2i$ и $z_{2} =1-5i$; 2) $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$; 3) $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$.

Решение:

Воспользуемся формулой из примечания 4.

1) Для чисел $z_{1} =1+2i$ и $z_{2} =1-5i$ получим:

[|z_{1} -z_{2} |=sqrt{(1-1)^{2} +(2+5)^{2} } =sqrt{0^{2} +7^{2} } =sqrt{49} =7.]

2) Для чисел $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$ получим:

[|z_{1} -z_{2} |=sqrt{(sqrt{3} -0)^{2} +(0-sqrt{5} )^{2} } =sqrt{(sqrt{3} )^{2} +(-sqrt{5} )^{2} } =sqrt{3+5} =sqrt{8} =2sqrt{2} .]

3) Для чисел $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$ получим:

[|z_{1} -z_{2} |=sqrt{(sqrt{3} -0)^{2} +(9+7)^{2} } =sqrt{(sqrt{3} )^{2} +16^{2} } =sqrt{3+256} =sqrt{259} .]

Примечание 5

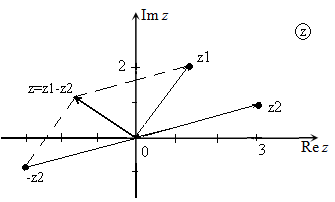
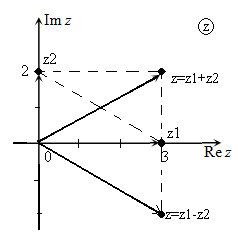
На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов комплексных чисел по правилу параллелограмма (рис. 3), используя следующий алгоритм:

построить на плоскости комплексное число $-z_{2} $;
найти сумму $-z_{2} $ и $z_{1} $ по правилу параллелограмма.

Рис. 3

Примечание 6

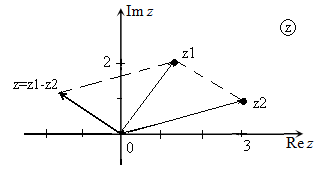
На комплексной плоскости операцию вычитания можно реализовать, используя другой алгоритм:

соединить точки, изображающие исходные комплексные числа;
достроить параллелограмм;
радиус-вектор, параллельный прямой, соединяющей точки, изображающие исходные комплексные числа, изображает разность исходных комплексных чисел – $z=z_{1} -z_{2} $.

Рис. 4

Пример 6

Построить на комплексной плоскости сумму и разность изображенных на плоскости комплексных чисел (рис.5): $z_{1} +z_{2} ,z_{1} -z_{2} $.

Рис. 5

Решение:

Для построения воспользуемся примечаниями 4 и 6.

Рис. 6

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Алгебраическая формула

Любые два вещественных числа можно сложить, и результатом сложения тоже является вещественное число. Это же верно и для комплексных чисел: любые два комплексных числа можно сложить, и их сумма (результат сложения) — это комплексное число. Причем сложение комплексных чисел сводится к сложению вещественных чисел. А именно: пусть даны два комплексных числа

z1=x1+iy1,z2=x2+iy2.z_1 =x_1 +iy_1, z_2 =x_2 +iy_2.

Их сумма — это комплексное число, определяемое формулой

z1+z2=(x1+x2)+i(y1+y2).z_1+z_2 = (x_1+x_2) +i(y_1+y_2).

Таким образом, вещественная часть суммы комплексных чисел — это сумма вещественных частей слагаемых, и мнимая часть суммы комплексных чисел — сумма мнимых частей слагаемых. Это тоже можно записать в виде формул:

Re(z1+z2)=Re z1+Re z2,mathrm{Re}left(z_1+z_2right) = mathrm{Re},z_1 + mathrm{Re},z_2, quad

Im(z1+z2)=Im z1+Im z2.mathrm{Im}left(z_1+z_2right) = mathrm{Im},z_1 + mathrm{Im},z_2.

Для комплексных чисел, как и для вещественных, определена операция вычитания. Найти разность z1−z2z_1-z_2 — это все равно что найти сумму z1+(−z2)z_1+(-z_2), где число −z2-z_2 получается из z2z_2 сменой знака вещественной и мнимой частей.

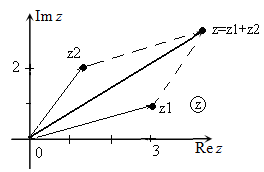
Геометрическая интерпретация сложения

Нам известно, что каждому комплексному числу x+yix+yi соответствует точка плоскости с координатами (x,y)(x,y). Вектор, проведенный от начала координат к точке (x,y)(x,y), называется радиус-вектором этой точки. Радиус-вектор точки (3,2)(3,2), соответствующей комплексному числу 3+2i3+2i, изображен на следующем рисунке:

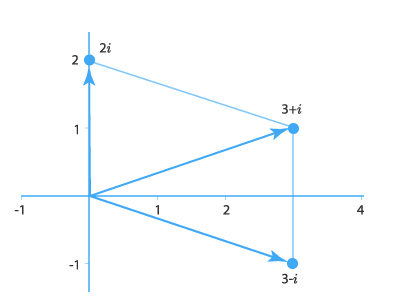
При сложении комплексных чисел соответствующие им радиус-векторы тоже складываются. Изобразить это на рисунке можно с помощью известного правила параллелограмма. На следующем рисунке с помощью векторов проиллюстрировано сложение комплексных чисел (3−i)+2i=3+i(3-i) + 2i = 3+i:

Решение примеров на сложение комплексных чисел

Пример 1

Найти сумму комплексных чисел z1+z2z_1+z_2, где:

a) z1=3+2i,z2=5−i;a) z_1 = 3+2i, z_2 = 5-i;

b) z1=−i,z2=4+i;b) z_1 = -i, z_2 = 4+i;

c) z1=−3−4i,z2=3+5i.c) z_1 = -3-4i, z_2 = 3+5i.

Решение
a) z1+z2=(3+2i)+(5−i)=(3+5)+(2−1)i=8+i;a) z_1 + z_2 = (3+2i) + (5-i) = (3+5) + (2-1)i = 8+i;

b) z1+z2=(−i)+(4+i)=(0+4)+(−1+1)i=4+0⋅i=4;b) z_1 + z_2 = (-i) + (4+i) = (0+4) + (-1+1)i = 4 + 0 cdot i = 4;

c) z1+z2=(−3−4i)+(3+5i)=(−3+3)+(−4+5)i=0+i=i.c) z_1 + z_2 = (-3-4i) + (3+5i) = (-3+3) + (-4+5)i = 0+i =i.

Пример 2

Найти разность комплексных чисел z1−z2z_1-z_2, где:

a) z1=3+2i,z2=5−i;a) z_1 = 3+2i, z_2 = 5-i;

b) z1=−i,z2=−3−2i.b) z_1 = -i, z_2 = -3-2i.

Решение

a) z1−z2=(3+2i)−(5−i)=(3−5)+(2−(−1))i=−2+3i;a) z_1 – z_2 = (3+2i) – (5-i) = (3-5) + (2-(-1))i = -2+3i;

b) z1−z2=(−i)+(−3−2i)=(0−(−3))+(−1−(−2))i=3+i.b) z_1 – z_2 = (-i) + (-3-2i) = (0-(-3)) + (-1-(-2))i = 3 + i.

Источник

Сложение комплексных чисел

Пример
1

Сложить
два комплексных числа
,

Для
того чтобы сложить два комплексных
числа нужно сложить их действительные
и мнимые части:

Просто,
не правда ли? Действие настолько очевидно,
что не нуждается в дополнительных
комментариях.

Таким
нехитрым способом можно найти сумму
любого количества слагаемых: просуммировать
действительные части и просуммировать
мнимые части.

Для
комплексных чисел справедливо правило
первого класса:

–от
перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример
2

Найти
разности комплексных чисел
и,
если,

Действие
аналогично сложению, единственная
особенность состоит в том, что вычитаемое
нужно взять в скобки, а затем – стандартно
раскрыть эти скобки со сменой знака:

Результат
не должен смущать, у полученного числа
две, а не три части. Просто действительная
часть – составная:
.
Для наглядности ответ можно переписать
так:.

Рассчитаем
вторую разность:

Здесь
действительная часть тоже составная:

Чтобы
не было какой-то недосказанности, приведу
короткий пример с «нехорошей» мнимой
частью:
.
Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал
момент познакомить вас со знаменитым
равенством:

Пример
3

Найти
произведение комплексных чисел
,

Очевидно,
что произведение следует записать так:

Что
напрашивается? Напрашивается раскрыть
скобки по правилу умножения многочленов.
Так и нужно сделать! Все алгебраические
действия вам знакомы, главное, помнить,
что
и
быть внимательным.

Повторим,
школьное правило умножения многочленов:
Чтобы умножить многочлен на многочлен
нужно каждый член одного многочлена
умножить на каждый член другого
многочлена.

Я
распишу подробно:

Надеюсь,
всем было понятно, что

Внимание,
и еще раз внимание, чаще всего ошибку
допускают в знаках.

Как
и сумма, произведение комплексных чисел
перестановочно, то есть справедливо
равенство:
.

В
учебной литературе и на просторах Сети
легко найти специальную формулу для
вычисления произведения комплексных
чисел. Если хотите, пользуйтесь, но мне
кажется, что подход с умножением
многочленов универсальнее и понятнее.
Формулу приводить не буду, считаю, что
в данном случае – это забивание головы
опилками.

Деление комплексных чисел

Пример
4

Даны
комплексные числа
,.
Найти частное.

Составим
частное:

Деление
чисел осуществляется методом
умножения знаменателя и числителя на
сопряженное знаменателю выражение.

Вспоминаем
бородатую формулу
и
смотрим на нашзнаменатель:
.
В знаменателе уже есть,
поэтому сопряженным выражением в данном
случае является,
то есть

Согласно
правилу, знаменатель нужно умножить на
,
и, чтобы ничего не изменилось, домножить
числитель на то же самое число:

Далее
в числителе нужно раскрыть скобки
(перемножить два числа по правилу,
рассмотренному в предыдущем пункте). А
в знаменателе воспользоваться формулой
(помним,
чтои
не путаемся в знаках!!!).

Распишу
подробно:

В
ряде случаев перед делением дробь
целесообразно упростить, например,
рассмотрим частное чисел:
.
Перед делением
избавляемся от лишних минусов: в числителе
и в знаменателе выносим минусыза
скобки и сокращаем эти минусы:
.
Для любителей порешать приведу правильный
ответ:

Редко,
но встречается такое задание:

Пример
5

Приём
тот же самый – умножаем знаменатель и
числитель на сопряженное Дано комплексное
число
.
Записать данное число в алгебраической
форме (т.е. в форме).

знаменателю
выражение. Снова смотрим на формулу
.
В знаменателе уже есть,
поэтому знаменатель и числитель нужно
домножить на сопряженное выражение,
то есть на: