
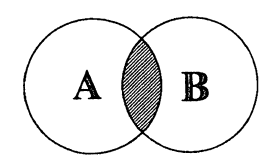
Объединение A и B
Объедине́ние мно́жеств (тж. су́мма или соедине́ние) в теории множеств — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств 




Содержание
- 1 Определения
- 1.1 Объединение двух множеств
- 1.2 Объединение семейства множеств
- 2 Свойства
- 3 Примеры
- 4 Примечания
- 5 См. также
Определения[править | править код]
Объединение двух множеств[править | править код]
Пусть даны два множества 

Объединение семейства множеств[править | править код]
Пусть дано семейство множеств 
Свойства[править | править код]
- Объединение множеств является бинарной операцией на произвольном булеане
- Операция объединения множеств коммутативна:
- Операция объединения множеств ассоциативна:
- Операция объединения множеств дистрибутивна относительно операции пересечения:[1]
- Пустое множество
является нейтральным элементом операции объединения множеств:
- Таким образом булеан вместе с операцией объединения множеств является моноидом;
- Операция объединения множеств идемпотентна:
Примеры[править | править код]
- Пусть
Тогда
Примечания[править | править код]
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 66. — 672 с. — ISBN 5-482-00445-7.
См. также[править | править код]
- Дизъюнктное объединение
- Операции над множествами
Теория множеств |
||
|---|---|---|
| Обзор |
|
|
| Аксиомы |
|
|
| Операции |
|
|
|
|
|
| Типы множеств |
|
|
| Теории |
|
|
|
|
|
| Теоретики множеств |
|
|
|
Макеты страниц
Суммой (или, иначе, объединением) двух множеств называют множество, содержащее все такие и только такие элементы, которые являются элементами хотя бы одного из этих множеств. Сумму множеств А и В обозначают
через А и  Как легко видеть, сумма множеств обладает свойствами, подобными свойствам суммы чисел: коммутативностью (переместительностью) и ассоциативностью (сочетательностью), т. е. для любых двух множеств А и В мы имеем
Как легко видеть, сумма множеств обладает свойствами, подобными свойствам суммы чисел: коммутативностью (переместительностью) и ассоциативностью (сочетательностью), т. е. для любых двух множеств А и В мы имеем  , а для любых трех множеств А, В, С имеем
, а для любых трех множеств А, В, С имеем  . Аналогично определяют сумму большего, даже бесконечного количества множеств: это множество, содержащее все такие и только такие элементы, которые являются элементами хотя бы одного из слагаемых.
. Аналогично определяют сумму большего, даже бесконечного количества множеств: это множество, содержащее все такие и только такие элементы, которые являются элементами хотя бы одного из слагаемых.
Легко доказать, что сумма двух счетных множеств также есть счетное множество. Пусть

— два счетных множества. Образуем счетную последовательность, выписывая поочередно по одному члену из каждой из двух последовательностей (2), т. е. образуем последовательность

Множество всех членов последовательности (3) будет, очевидно, суммой множеств членов последовательностей (2). Если у этих последовательностей имеются одинаковые члены, то для получения последовательности, содержащей толвко различные члены и являющейся суммой множеств членов последовательностей (2), достаточно из последовательности (3) исключить каждый член, равный какому-либо из предшествующих членов.
Аналогично можно легко доказать, что сумма трех и, вообще, любого конечного числа счетных множеств есть счетное множество. Докажем теперь, что сумма счетного множества счетных множеств тоже есть счетное множество.
Допустим, что мы имеем бесконечную последовательность бесконечных последовательностей  . Члены последовательности
. Члены последовательности  обозначим через
обозначим через  Сумма множеств членов наших последовательностей будет, следовательно, множеством всех членов такой бесконечной таблицы:
Сумма множеств членов наших последовательностей будет, следовательно, множеством всех членов такой бесконечной таблицы:

Теорема будет доказана, если мы покажем, что все элементы этой таблицы можно расположить в виде обыкновенной бесконечной последовательности. Это можно сделать с помощью так называемого диагонального метода, а именно, выписывая сперва единственный член, у которого сумма нижнего и верхнего индексов составляет 2, затем два члена с суммой индексов 3, далее три члена с суммой индексов 4 и т.  Мы получим таким образом обыкновенную бесконечную последовательность
Мы получим таким образом обыкновенную бесконечную последовательность

Если, в частности, принять  то бесконечная последовательность (4) содержала бы все рациональные положительные числа, причем каждое из них — бесконечное число раз, так как
то бесконечная последовательность (4) содержала бы все рациональные положительные числа, причем каждое из них — бесконечное число раз, так как  . Чтобы получить бесконечную последовательность, в которой каждое рациональное положительное число встречается один и только один раз, достаточно оставить в нашей последовательности только несократимые дроби. Мы видим, таким образом, что множество всех положительных рациональных чисел счетно. Ясно также, что и множество всех отрицательных рациональных чисел счетно, а поскольку сумма двух счетных множеств есть счетное множество, мы можем расположить в бесконечную последовательность все рациональные числа, отличные от нуля, а добавив к ее началу число 0, получаем теорему, что множество всех рациональных чисел счетно.
. Чтобы получить бесконечную последовательность, в которой каждое рациональное положительное число встречается один и только один раз, достаточно оставить в нашей последовательности только несократимые дроби. Мы видим, таким образом, что множество всех положительных рациональных чисел счетно. Ясно также, что и множество всех отрицательных рациональных чисел счетно, а поскольку сумма двух счетных множеств есть счетное множество, мы можем расположить в бесконечную последовательность все рациональные числа, отличные от нуля, а добавив к ее началу число 0, получаем теорему, что множество всех рациональных чисел счетно.
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- От редакции польского издания
- ГЛАВА I. О МНОЖЕСТВАХ И ИХ СВОЙСТВАХ
- 2. Равенство множеств
- 4. Пустое множество
- 5. Конечные множества
- 6. Равночисленные множества
- 7. Взаимно однозначное соответствие
- 8. Равномощные множества
- 9. Счетные множества
- 10. Сумма множеств
- 11. Несчетные множества
- 12. Континуум-гипотеза
- 13. Непересекающиеся множества
- 14. Сравнение мощностей бесконечных множеств
- 15. Аксиома выбора
- 16. Алгебра множеств
- 17. Упорядоченные множества
- 18. Подобные упорядоченные множества
- 19. Плотные упорядоченные множества. Сечения. Щели
- 20. Заполнение щелей
- 21. Вполне упорядоченные множества
- 22. Принцип трансфинитной индукции
- 23. Принцип математической индукции
- 24. Функции
- 25. Декартово произведение
- 26. Метрические пространства
- 27. Евклидовы пространства
- 28. Борелевские множества
- 29. Открытые и замкнутые множества
- 30. Производное множество и замыкание множества
- 31. Топология
- 32. Односторонние поверхности
- 33. Проблема четырех красок
- ГЛАВА II. О КОНГРУЭНТНОСТИ МНОЖЕСТВ. КОНГРУЭНТНОСТЬ МНОЖЕСТВ ПРИ КОНЕЧНОМ РАЗБИЕНИИ
- 2. Движения множеств
- 3. Конгруэнтность множеств при конечном разбиении
- 4. Преобразования сжатия
На чтение 13 мин Просмотров 2.1к. Опубликовано 16.12.2021
Содержание
- Теория множеств
- Что такое множество в математике и как оно обозначается
- Множество натуральных чисел
- Множество целых чисел
- Множество рациональных чисел
- Операции над множествами
- Объединение
- Пересечение множеств
- Дополнение
- Универсум и отрицание
- Разность множеств
- Формулы включений и исключений
- Свойства операций над множествами
- Счетные и несчетные множества
- Исследование множеств с помощью координатной прямой
- Примеры из реальной жизни
- Геометрические фигуры
- Отрезки
- Еще пример
Теория множеств
Говоря простым языком, множество — это элементарный математический объект, который содержит определенный набор данных, предметов или чисел. Это исходное математическое понятие, которое невозможно представить другими терминами. Именно поэтому множество описывается как набор разрозненных элементов, мыслимое как единое целое. Понятие множества ввел немецкий математик Георг Кантор, который развил собственную теорию трансфинитных чисел, позволяющую оперировать вполне упорядоченными бесконечными множествами.
Георг Кантор разработал уникальную программу стандартизации всех математических знаний, согласно которой любой математический объект является тем или иным множеством. К примеру, согласно канторовской теории, любое натуральное число — это одноэлементное множество, принадлежащее надмножеству натурального ряда. Натуральный ряд, в свою очередь, считается подмножеством целого ряда, а целое множество — подмножеством действительного или вещественного ряда.
Теория Георга Кантора вызвала широкий резонанс в математических кругах. Многие современники негативно отзывались о его работах, особенно его учитель Леопольд Кронекер, который не принимал канторовского определения натурального числа. Несмотря на это, теория множеств получила признание позже, когда группа французских математиков под псевдонимом Никола Бурбаки предприняла попытку перевести весь математический аппарат на теоретико-множественный язык.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Пример:
А = {а, в, с, у} – А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:
- конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
- бесконечные — не являющиеся конечными (например, числовые);
- пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Множество натуральных чисел
К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.
N = {9, 11, 13, 15……}.
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Z = {-112, -60, -25, 0, 36, 58, 256}.
Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Q={-½; 0; ½, 5; 10}.
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
5 = 5/1 = 10/2 = 25/5;
0,45 = 45/100 = 9/20.
Следовательно, N и Z являются подмножествами Q.
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Объединение

Пересечение множеств
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
$$ A cap B = {x|x in Bbb A и x in Bbb B } $$

Если множества не пересекаются, то $A cap B = varnothing $ — пустое множество в пересечении. Если $B subseteq A$ — подмножество, то $A cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A cap B$ = {f|f-квадрат}.
Если A = ${n|n⋮3, n in Bbb N }$ — натуральные числа, кратные 3, B = ${n|n⋮5, n in Bbb N }$ — натуральные числа, кратные 5, то $A cap B = {n|n⋮15, n in Bbb N}$ — натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A cap B = varnothing$.
Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:

Примеры универсумов:
- При рассмотрении целочисленных задач, универсум – это множество целых чисел.
- При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
- При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Отрицание (абсолютное дополнение) множества A — множество всех элементов универсума, не принадлежащих A:
$$ bar{A} = {x|x notin A } $$
Читается «не A».
У отрицания есть любопытное свойство: $bar{bar{Α}} = Α $(два раза «нет» — это «да»).

Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $bar{A} = {1;2;6;7}$
Если U = ${x|x in Bbb R}$ — все действительные числа, A = ${x|x gt 0, x in Bbb R }$ — все положительные действительные числа, то $ bar{A} = {x|x le 0, x in Bbb R}$.
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
$$ AB = {x|x in Bbb A , x notin B} $$
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:


Получается, что отрицание – частный случай разности: $ bar{A} = {x|x in Bbb U, x notin A } $= UA
«Не A» — это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A cup B)$?

Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A cup B) = n(A)+ n(B)-n(A cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.

Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A cap B)+n(A cap C)+n(B cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A cap B cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A cup B cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A cap B)+n(A cap C)+n(B cap C) )+n(A cap B cap C) $$
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:
- умножения S ∩ D = D ∩ S;
- сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
- умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
- сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
- умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
- умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
- сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
Транзитивность — законы включения:
- если S ⊆ Fи F ⊆ J, то S ⊆ J;
- если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
- S ∩ S = S;
- S ∪ S = S.
О других свойствах операций можно узнать из картинки:

Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно — несчетным. Другими словами, счетная единица — это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Теория множеств — достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.
Исследование множеств с помощью координатной прямой
Исследовать и выражать пересечения и объединения числовых множеств удобно с помощью координатной прямой и выделяемых на ней числовых промежутков. Любая выбранная точка разбивает все расположенные на такой прямой числа на два открытых числовых луча. Например, точка с координатой $36,6$ создаст промежутки, записываемые как $(−∞, 36,6)$, $(36,6, +∞)$. Сама точка не входит в состав ни одного из них, поэтому числовая прямая, представляющая собой множество всех действительных чисел $R = (−∞, +∞)$, представляет собой в данном случае объединение $ (−∞, −36,6) cup {36,6} cup (36,6, +∞)$.
Если рассматриваемую точку со значением $36,6$ добавить к одному из открытых числовых лучей, т.е. промежутку $(−∞, 36,6)$ или $(36,6, +∞)$, то такой промежуток перестанет быть открытым. Это записывается как $(−∞, 36,6]$ или $[36,6, +∞)$, т.е. вхождение граничного числа в состав числового луча обозначается квадратной скобкой. Множество действительных чисел $R$ в этом случае будет выглядеть как
$(−∞, 36,6] cup (36,6, +∞)$ либо $(−∞, 36,6) cup [36,6, +∞)$.
Если разбить числовую прямую на части не точкой, а отрезком или лучом, то все рассмотренные закономерности будут соблюдаться и в этих случаях. Более того, они соблюдаются и при разбиении самих числовых промежутков (отрезков, лучей).
Например, точка с координатой $14$ на промежутке $(5, 51]$ разобьет его на промежутки $(5, 14) ∪ {14} ∪ (14, 51]$. Включив точку в один из промежутков, можно получить такие записи, как $(5, 14] cup (14, 51]$, $(5, 14) cup [14, 51]$. Приняв за разбивающую точку число $51$, ограничивающее рассматриваемый промежуток справа и входящее в его состав, получим объединение множества ${51}$ и интервала $(5, 51)$, т.е. $(5, 51] = (5, 51) cup {51}$.
Подобные закономерности справедливы и в случаях, когда координатная прямая разбивается на промежутки несколькими точками. Например, числа $−6$, $0$ и $7$ разобьют ее на промежутки $(−∞, −6)$, $(−6, 0)$, $(0, 7)$, $(7, +∞)$, а множество действительных чисел $R$ будет представлено как $(−∞, −6) ∪ {−6} ∪ (−6, 0) ∪ {0} ∪ (0, 7) ∪ {7} ∪ (7, +∞)$.
С помощью координатной прямой удобно анализировать пересечения и объединения множеств. Они изображаются друг под другом на координатных прямых с совпадающими точками и направлениями отсчета. Для отображения объединения множеств координатные прямые отмечают слева квадратной скобкой, для обозначения пересечения используется фигурная скобка.
На дополнительной координатной прямой, размещаемой под исходными, изображаются искомые пересечение или объединение. На ней все граничные точки исходных множеств отмечают поперечными чертами, а после уточнения — полыми или сплошными точками. Графически вхождение промежутка в пересечение или объединение изображается штриховкой, вхождение точки — сплошной точкой, невхождение – полой.
Пересечение множеств $A$ и $B$ графически отображается промежутками, над которыми есть штриховка, с добавлением отдельных точек, принадлежащих обоим множествам. Объединение графически проявляется там, где есть штриховка хотя бы у одного из множеств, а также всех сплошных точек.
Пример 1
Найти пересечение и объединение множеств $A = [-3, 4)$ и $B = [0, 7)$ .
Для решения применим графический метод:
Рисунок 1. Графическое решение задачи. Автор24 — интернет-биржа студенческих работ
Видно, что объединение множеств представляет собой диапазон от крайней левой точки $-3$ включительно до крайней правой $7$ исключая ее. Пересечение множеств начинается от числа $0$. Оно входит в оба множества и ограничивает пересечение слева. Правой границей пересечения является $4$, но оно не входит в первое множество, поэтому здесь граница интервала будет открытой.
Ответ:
$A cap B = [0, 4); A cup B = [-3, 7); $
Примеры из реальной жизни
Геометрические фигуры
Допустим, существует множество X, которое содержит прямоугольники с разными длинами сторон. Также существует множество Y, содержащее ромбы с разными углами. Из курса геометрии мы знаем, что ромб — это параллелограмм, у которого все стороны равны, а прямоугольник — это параллелограмм, у которого равны все углы. В множествах X и Y могут встретиться ромбы с углами по 90 градусов или прямоугольники с одинаковыми сторонами. Фигура, у которой все углы прямые, а все стороны равны — это квадрат. Соответственно, пересечением множеств ромбов X и прямоугольников Y является множество квадратов Z.
Отрезки
Пусть у нас есть два отрезка, которые задаются координатами X = [1, 3] и Y = [2, 4]. Пересечением данных множеств будет отрезок [2, 3], так как именно эти числа входят в диапазон значений обоих отрезков на числовой оси.
Еще пример
Давайте попробуем узнать пересечение пятиэлементных множеств простых и четных чисел. Простое число — это число, которое делится только на себя и на единицу. Четное число — число, которое делится на 2 без остатка. Итак, наши множества S = {2, 3, 5, 7, 11} и E = {2, 4, 6, 8, 10}. Введем эти данные в онлайн-калькулятор и получим результат в виде P = {2}.
Пусть
![]() –
–
конечное множество, содержащее![]() элементов, тогда теорема 6 § 1 выполняется,
элементов, тогда теорема 6 § 1 выполняется,
если положить![]() .
.
В дальнейшем
кардинальное число конечного множества
будем отождествлять с числом его
элементов.
Таким ообразом,
теория мощностей конечных множеств не
выводит нас за рамки арифметических
натуральных чисел. Новые ситуации
возникают только тогда, когда мы переходим
к рассмотрению бесконечных множеств.
О п р е д е л е
н и е. Множество
![]() называется счетным, если оно конечно
называется счетным, если оно конечно
или равномощно множеству кардинальных
чисел.
Очевидно, что любые
два бесконечные счетные множества
равномощны (смотреть теорему 1, § 1).
Кардинальное число бесконечных счетных
множеств обозначим через а
(![]() –
–
мощность радя натуральных множеств).
В главе III
мы определили последовательность как
функцию, областью определения которой
служит множество натуральных чисел. Из
этого определения следует, что бесконечное
множество
![]() счетно тогда и только тогда, когда оно
счетно тогда и только тогда, когда оно
служит множеством значений
последовательности с попарно различными
числами.
Допуская некоторую
вольность, можно сказать, что множество
![]() счетно, если его элементы можно
счетно, если его элементы можно
«расположить» в бесконечную
последовательность![]() .
.
Теорема 1. Каждое
непустое счетное множество является
множеством значений некоторой бесконечной
последовательности. И обратно, множество
значений произвольной бесконечной
последовательности счетно и непусто.
Д
о
к
а
з
а
т
е
л
ь
с
т
в
о.
Конечное множество
![]() есть множество значений бесконечной
есть множество значений бесконечной
последовательности.
![]() .
.
Бесконечное счетное
множество есть по определению множество
значений некоторой бесконечной
последовательности.
Для доказательства
обратного утверждения рассмотрим
множество
![]() значений бесконечной последовательности
значений бесконечной последовательности![]() .
.
Пусть
![]() и
и![]() ,
,
где![]() или же
или же![]() ,
,
если нет такого![]() ,
,
что![]() .
.
По индукции легко
доказать, что для каждого
![]() существует такое
существует такое![]() ,
,
что![]() .
.
Отсюда следует, что![]() и, таким образом, все числа последовательности
и, таким образом, все числа последовательности![]() различны. Осталось показать, что каждый
различны. Осталось показать, что каждый
элемент множества![]() будет числом последовательности
будет числом последовательности![]() .
.
Предположим, что
множество
![]() не является
не является
членом последовательности
![]() }
}
непусто,
и пусть
![]() –
–
наименьший его элемент. Очевидно, что![]() .
.
Если
![]() ,
,
то![]() –
–
член последовательности![]() ,
,
например,![]() .
.
Пусть![]() .
.
Наименьшее такое
число
![]() ,
,
что![]() ,
,
как раз и равно![]() .
.
По определению
последовательности
![]() тогда
тогда![]() ,
,
что противоречит выбору![]() .
.
Теорема доказана.
Аналогично
доказывается
Теорема 2. Любое
подмножество счетного множества счетно.
Теорема 3. Сумма
двух счетных множеств счетна.
Д
о
к
а
з
а
т
е
л
ь
с
т
в
о.
Т.к. случай, когда одно из данных множеств
пусто, не представляет трудности, будем
считать, что
![]() –
–
множество значений последовательности![]() ,
,
![]() –
–
множество значений последовательности
![]() .
.
Тогда сумма
![]() есть множество значений полседовательности
есть множество значений полседовательности![]() ,
,
и поэтому счетно.
Можно доказать по
индукции, что сумма любого конечного
числа счетных множеств счетно.
Следствие 4.
Сумма конечного и счетного множества
счетна.
Теорема 5.
Декартово произведение двух счетных
множеств счетно.
Д
о
к
а
з
а
т
е
л
ь
с
т
в
о.
Если
![]() и
и![]() счетные и бесконечные, то
счетные и бесконечные, то![]() ,
,![]() (в силу теоремы 1 §3, главаIII).
(в силу теоремы 1 §3, главаIII).
Если одно из
множеств
![]() ,
,![]() или оба они конечны, то
или оба они конечны, то![]() равномощно некоторому подмножеству
равномощно некоторому подмножеству
произведения![]() ,
,
т.е. подмножеству множества![]() .
.
Таким образом,
утверждение данной теории следует из
теоремы 2.
Теорема 7. Если
![]() –
–
бесконечная последовательность, члены
которой – также бесконечные
последовательности, то множество![]() элементов
элементов
x,
являющихся членами последовательности
![]() ,
,
счетно.
Д
о
к
а
з
а
т
е
л
ь
с
т
в
о.
По определению
![]() .
.
Таким образом,
![]() –
–
это множество значений последовательности![]() ,
,
определенной равенством![]() .
.
°Теорема
8. Если
![]() –
–
последовательность, члены которой –
непустые счетные множества, то сумма![]() счетна.
счетна.
Д
о
к
а
з
а
т
е
л
ь
с
т
в
о.
Обозначим через
![]() множество последовательностей
множество последовательностей![]() ,
,
для которых![]() будет множеством значений. По условию
будет множеством значений. По условию![]() для каждого
для каждого![]() .
.
Тогда, согласно
аксиоме выбора, существует такая
последовательность
![]() ,
,
что![]() для каждого
для каждого![]() .
.
Таким образом, сумма![]() есть множество тех
есть множество тех![]() ,
,
для которых существуют такие![]() ,
,
что![]() .
.
В силу теоремы 7 это множество счетно.
Замечание.
Необходимость применения аксиомы выбора
в доказательстве теоремы 8 обусловлена
тем, что хотя для каждого множества
существует бесконечная последовательность,
состоящая из всех его элементов, но для
данного множества таких последовательностей
бесконечно много и у нас нет способа
выделения какой-то одной из них. Другими
словами, у нас нет способа сопоставления
каждому счетному множеству бесконечной
последовательности, содержащей все его
элементы.
Примеры счетных
множеств.
Пример 1.
Множество целых чисел счетно.
Действительно,
это множество представляет собой сумму
![]() ,
,
где![]() –
–
множество чисел![]() .
.
Т.к.![]() (равномощность этих множеств устанавливает
(равномощность этих множеств устанавливает
функция![]() ),
),
то множество![]() и
и![]() оба счетны, а тогда
оба счетны, а тогда![]() также счетна.
также счетна.
Пример 2.
Множество рациональных чисел счетно.
В самом деле,
последовательность
![]() ,
,
заданная равенством![]() ,
,
содержит в качестве своих членов все
положительные рациональные числа и
только их. Значит, множество всех
положительных рациональных чисел
счетно, и поэтому (смотреть пример 1)
множество всех рациональных чисел также
счетно.
Пример 3.
Множество многочленов от одной переменной
с целыми коэффицентами счетно.
Действительно,
каждому многочлену с целыми коэффицентами
взаимно однозначно соответствует
последовательность его коэффицентов,
а множество всех конечных последовательностей
целых чисел (согласно теореме 6) счетно.
Пример 4.
Множество алгебраических чисел счетно.
Каждому многочлену
соответствует конечная последовательность
всех его корней: в качестве первого
члена этой последовательности берем
корень с наименьшим модулем и с наименьшим
аргументом среди всех корней этого
модуля; в качестве второго члена берем
отличный от первого, с наименьшим
возможным модулем и с наименьшим
аргументом среди всех корней этого
модуля и т.д. Согласно теореме 7, множество
всех алгебраических чисел счетно.
Этот результат
можно получить из теоремы 8, но тогда
пришлось бы пользоваться аксиомами
выбора.
Математика — это точная абстрактная наука, оперирующая своими специальными понятиями, структурами и символами. Основными методами в математических исследованиях являются строгие логические рассуждения, а объектами изучения — математические модели. Но абстрактность математики не означает ее отрыв от реальной жизни. Реальные задачи описываются в математических терминах, как правило в безразмерном виде. Это есть так называемая
математическая модель явления. При решении уже поставленной математической задачи используются абстрактные математические методы.
Одна и та же математическая модель может описывать свойства различных реальных явлений. Само реальное явление рассматривается вновь после решения математической задачи и ее анализа, на основании которого могут быть сделаны выводы
не только о состоянии явления, но и о его развитии. В этом смысле без математики нет науки. Еще великий Леонардо да Винчи писал: «Никакой достоверности нет в науках там, где нельзя применить ни одну из математических наук, ив том, что не имеет связи с математикой.» И еще: » Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства.»
Математические методы играют огромную роль в образовании современного высококвалифицированного специалиста в технических областях, предоставляя ему аппарат исследования, дисциплинируя, приучая к строгим логическим рассуждениям.
Поскольку язык и методы математики широко используются при современном преподавании всех естественно-научных и технических дисциплин, математика изучается с первого семестра в любом высшем техническом учебном заведении, и на нее выделяется значительная часть бюджета времени студента.
Под множеством понимают любой набор определенных и различимых между собой объектов, рассматриваемых как единое целое. Это высказывание не является определением, поскольку слово « множество» заменено словом «набор». Близкими к понятию «множество» являются понятия: собрание, совокупность, комплекс, система и т. п. Вместе с тем здесь имеется три важных момента.
Объекты, входящие во множество, определенные (т. е. для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет), различимы между собой (во множестве не может быть двух или более одинаковых объектов) и все объекты, входящие во множество, мыслятся как единое целое (все объекты рассматриваются в совокупности, а от свойств отдельных объектов абстрагируются).
Множества обозначают прописными буквами латинского алфавита. Объекты, входящие во множество, называют элементами и их обозначают строчными буквами. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае множество называется бесконечным.
Множество может быть задано при помощи правила, позволяющего определить, является ли данный объект элементом множества или нет. В записи правило, задающее множество, отделено вертикальной чертой. Например, пусть множество В есть множество решений уравнения 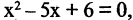 тогда В можно записать так
тогда В можно записать так 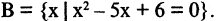 Элементами множества В являются числа 2 и 3, то есть
Элементами множества В являются числа 2 и 3, то есть 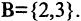
Конечное множество может быть задано перечислением входящих в него и разделенных запятой элементов, например, 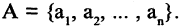 Множество может содержать и всего лишь один элемент. Множество, не содержащее вообще ни одного эле-
Множество может содержать и всего лишь один элемент. Множество, не содержащее вообще ни одного эле-
мента, называется пустым и обозначается символом 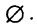 Например, пусть
Например, пусть 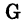 есть множество точек на плоскости, удовлетворяющих условию
есть множество точек на плоскости, удовлетворяющих условию 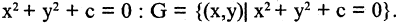 При
При 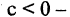 окружность, при
окружность, при 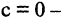 одна точка, а при
одна точка, а при 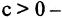 пустое множество.
пустое множество.
Для указания того факта, что объект принадлежит данному множеству, используют знак 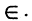 Например,
Например, 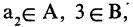
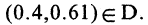 Если же объект не принадлежит данному множеству, то пишут знак
Если же объект не принадлежит данному множеству, то пишут знак 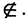 Например,
Например, 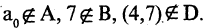
Множество В называется подмножеством множества А, если каждый элемент В одновременно является элементом множества А. Это записывается так: 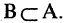
Пример:
Пусть заданы множества 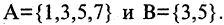 Очевидно, что В есть подмножество А, т. е.
Очевидно, что В есть подмножество А, т. е.  Из определения следует, что множество А есть подмножество самого себя, т. е.
Из определения следует, что множество А есть подмножество самого себя, т. е. 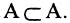 Говорят, что А — самое широкое подмножество А. Пустое множество является самым узким подмножеством любого множества. Множество А и пустое множество
Говорят, что А — самое широкое подмножество А. Пустое множество является самым узким подмножеством любого множества. Множество А и пустое множество 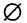 называются несобственными подмножествами множества А. Все другие подмножества А называются собственными подмножествами А.
называются несобственными подмножествами множества А. Все другие подмножества А называются собственными подмножествами А.
Пример:
Если 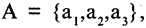 то оно имеет, следующие подмножества:
то оно имеет, следующие подмножества: 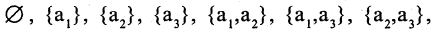
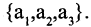 Всего 8 подмножеств.
Всего 8 подмножеств.
Если конечное множество А состоит из п элементов, то оно имеет ровно 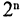 подмножеств. Из них ровно
подмножеств. Из них ровно 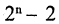 являются собственными подмножествами. Элементами множества могут также выступать и другие множества. В этом случае говорят не о множестве множеств, а о системе множеств. Частным случаем системы множеств является система всех подмножеств данного множества А и обозначается Р(А). Так, система подмножеств множества А из предыдущего примера имеет вид
являются собственными подмножествами. Элементами множества могут также выступать и другие множества. В этом случае говорят не о множестве множеств, а о системе множеств. Частным случаем системы множеств является система всех подмножеств данного множества А и обозначается Р(А). Так, система подмножеств множества А из предыдущего примера имеет вид
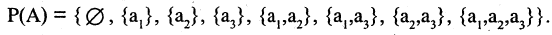
Замечание. Не следует путать символы  и
и  . Символ
. Символ  употребляется для обозначения отношения элемента к множеству. Символ
употребляется для обозначения отношения элемента к множеству. Символ  употребляется для обозначения отношения множества к множеству.
употребляется для обозначения отношения множества к множеству.
Зафиксированное каким-либо образом множество объектов, допустимых при данном рассмотрении, называют базовым или универсумом. Базовое множество обозначают буквой 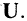 Примерами универсума являются: числа в арифметике, слова в языкознании, законы в юриспруденции и т.п.
Примерами универсума являются: числа в арифметике, слова в языкознании, законы в юриспруденции и т.п.

Операции над множествами
Множества можно складывать и вычитать, то есть совершать операции.
Равенство множеств
Множества А и В считаются равными, если они состоят из одних и тех же элементов. Равенство множеств обозначают так: А=В. Если множества не равны, то пишут: А 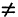 В. Отсюда следует, что запись равенства двух множеств «А=В» эквивалентна записи
В. Отсюда следует, что запись равенства двух множеств «А=В» эквивалентна записи 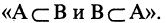
Пример. Доказать, что множество 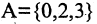 равно множеству В корней уравнения
равно множеству В корней уравнения 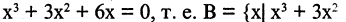
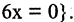
Для доказательства решим уравнение. Получим: 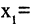
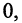
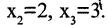 Следовательно,
Следовательно, 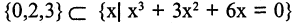 или
или 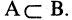 Затем непосредственной подстановкой убеждаемся, что любое из чисел 0,2, 3 удовлетворяет уравнению, следовательно
Затем непосредственной подстановкой убеждаемся, что любое из чисел 0,2, 3 удовлетворяет уравнению, следовательно 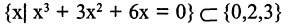 или
или 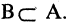 Теперь можно записать, что А=В.
Теперь можно записать, что А=В.
Объединение (сумма) множеств
Объединением множеств А и В называется такое множество С, каждый элемент которого содержится хотя бы в одном из множеств А или В. Обозначается: 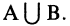 Пример. Если
Пример. Если 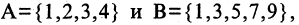
Можно рассматривать объединение 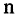 множеств:
множеств:
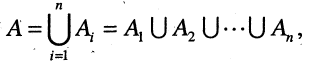
при этом в А входят все элементы, которые входят хотя бы в одно из множеств 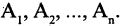 Например, множество всех дей-
Например, множество всех дей-
ствительных чисел 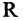 состоит из множества положительных чисел
состоит из множества положительных чисел 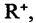 множества отрицательных чисел
множества отрицательных чисел 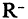 и множества
и множества 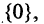 содержащего один элемент — ноль, то есть
содержащего один элемент — ноль, то есть 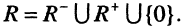
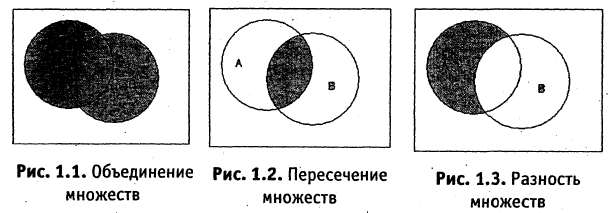
Для наглядного представления соотношений между несколькими подмножествами какого-либо универсума часто используются круги Эйлера или диаграммы Венна. Универсум представляется множеством всех точек некоторого прямоугольника, а его подмножества — соответствующими кругами. Операция объединения и другие операции иллюстрируются кругами Эйлера представленными на рис. 1.1-1.5.
Пересечение (умножение) множеств
Пересечением множеств А и В называется множество D, составленное из общих для множеств А и В элементов. Обозначение: 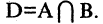 Например:
Например: 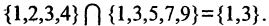
Можно рассматривать пересечение 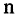 множеств:
множеств:
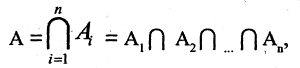
при этом в А входят только те элементы, которые входят во все множества 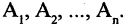 Пересечение двух множеств иллюстрируется на рис 1.2.
Пересечение двух множеств иллюстрируется на рис 1.2.
Пусть есть некоторое множество А. Говорят, что задано разбиение множества А на классы 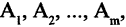 если
если
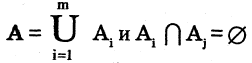
для всех 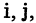 причем
причем 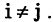

Классы — это такие подмножества разбиваемого множества, которые не имеют общих элементов, а их объединение образует исходное множество А. Следовательно, каждый элемент множества А входит в один и только в один класс.
Разность двух множеств
Разностью двух множеств А и В называется множество G, содержащее лишь те элементы из А, которые не входят в В. Обозначение: 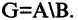 Отметим, что в А могут находиться не все элементы из вычитаемого множества В (см. рис. 1.3). Например,
Отметим, что в А могут находиться не все элементы из вычитаемого множества В (см. рис. 1.3). Например, 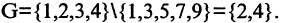
Если В — подмножество 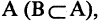 то разность
то разность 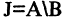 называется дополнением к В до А. Например, если
называется дополнением к В до А. Например, если 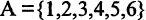 и
и 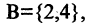 то множество
то множество 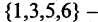 дополнение к В до А. Операция дополнения иллюстрируется на рис. 1.4. Дополнение к А до универсума
дополнение к В до А. Операция дополнения иллюстрируется на рис. 1.4. Дополнение к А до универсума 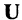 имеет особое обозначение:
имеет особое обозначение: 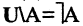 (см. рис. 1.5).
(см. рис. 1.5).
Пример. Пусть 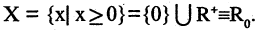 Такое множество называется множеством неотрицательных чисел.
Такое множество называется множеством неотрицательных чисел.
Тогда 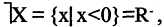 это множество отрицательных чисел.
это множество отрицательных чисел.
Операции над множествами подчиняются определенным законам. Перечислим их.
1.Коммутативный или переместительный закон

2.Ассоциативный или сочетательный закон
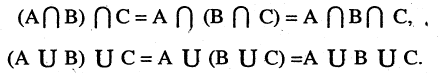
Так как порядок выполнения операций несущественен, то скобки в записи опускают.
3.Дистрибутивный или распределительный закон:
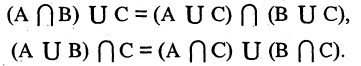
4.Закон идемпотентности:
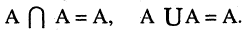
5.Закон поглощения:
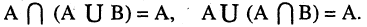
6.Закон двойственности де Моргана:

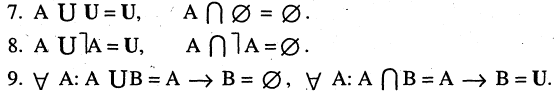
10.Если 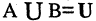 и одновременно
и одновременно 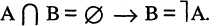
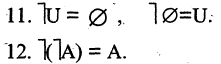
Из законов (1-12) следует принцип двойственности: всякое равенство, тождественно выполняемое в теории множеств, переходит также в тождественно выполняющееся равенство при замене знака объединения 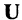 на знак пересечения
на знак пересечения 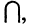 множество универсум
множество универсум 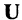 на пустое множество
на пустое множество 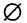 и наоборот.
и наоборот.
Прямое произведение множеств
Кортежем называют любую выделенную упорядоченную совокупность объектов (элементов кортежа). Синонимами понятия «кортеж» являются: упорядоченная система, упорядоченная совокупность, вектор, упорядоченный набор, «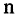 -ка» и др. Отличие кортежа от множества заключается в том, что компоненты кортежа упорядочены и могут полностью или частично совпадать. Два кортежа называются равными, если они имеют
-ка» и др. Отличие кортежа от множества заключается в том, что компоненты кортежа упорядочены и могут полностью или частично совпадать. Два кортежа называются равными, если они имеют
одинаковую длину, и все их соответствующие компоненты совпадают.
Элементы, составляющие кортеж, называются компонентами, которые в силу упорядоченности имеют номер: первый компонент, второй компонент, … 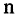 -ый компонент. Длиной кортежа называют число компонентов в кортеже. Когда вместо термина «кортеж» употребляется термин «вектор», то говорят соответственно о координатах и размерности вектора.
-ый компонент. Длиной кортежа называют число компонентов в кортеже. Когда вместо термина «кортеж» употребляется термин «вектор», то говорят соответственно о координатах и размерности вектора.
Примеры кортежей: 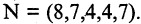 Это кортеж N длины 5, первый компонент которого — 8, второй — 7, третий — 4 и т. д.;
Это кортеж N длины 5, первый компонент которого — 8, второй — 7, третий — 4 и т. д.; 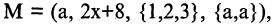 в этом случае
в этом случае 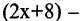 второй, а
второй, а 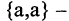 четвертый компонент кортежа М.
четвертый компонент кортежа М.
Прямым произведением двух множеств А и В (обозначается  называется множество, состоящее из всех тех и только тех пар, первый компонент которых принадлежит А, второй -В. Если первый сомножитель имеет
называется множество, состоящее из всех тех и только тех пар, первый компонент которых принадлежит А, второй -В. Если первый сомножитель имеет 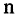 элементов, а второй —
элементов, а второй — 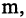 то их прямое произведение имеет
то их прямое произведение имеет 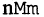 элементов, каждый из которых — упорядоченная пара. Например, если
элементов, каждый из которых — упорядоченная пара. Например, если 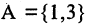 и
и 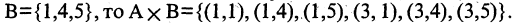 В общем случае, если
В общем случае, если 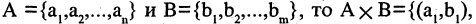
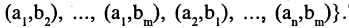 Тем самым прямым произведением
Тем самым прямым произведением 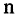 множеств
множеств 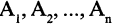 называется множество всех кортежей длины
называется множество всех кортежей длины 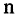 (
(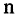 -ок), первый компонент которых принадлежит
-ок), первый компонент которых принадлежит 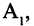 второй
второй 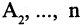 -тый —
-тый — 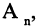 т. е.
т. е.
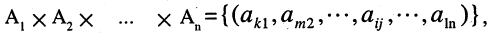
где 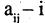 -ый элемент множества
-ый элемент множества 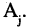
Если все множества 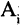 равны между собой, то есть
равны между собой, то есть 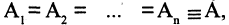 то прямое произведение множеств обозначается как
то прямое произведение множеств обозначается как 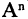
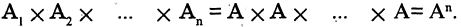
Например: пусть R — множество действительных чисел, тогда  множество упорядоченных пар вида
множество упорядоченных пар вида 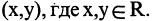 Геометрически R — множество точек числовой оси, тогда
Геометрически R — множество точек числовой оси, тогда 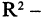 множество точек плоскости, где
множество точек плоскости, где 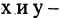 координаты этих точек. Прямое произведение часто называют декартовым произведением множеств. Множество Р называется графиком, если
координаты этих точек. Прямое произведение часто называют декартовым произведением множеств. Множество Р называется графиком, если
каждый его элемент является упорядоченной парой, следовательно, любое подмножество множества 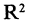 можно назвать графиком.
можно назвать графиком.
Проекцией кортежа 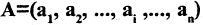 на і-ю ось
на і-ю ось 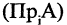 называется і-ый компонент кортежа, т. е.
называется і-ый компонент кортежа, т. е. 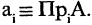 Проекция точки плоскости на первую ось
Проекция точки плоскости на первую ось 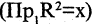 называется абсциссой, на вторую ось — ординатой
называется абсциссой, на вторую ось — ординатой 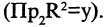 Из определения прямого произведения следует, что оно не коммутативно, т. е.
Из определения прямого произведения следует, что оно не коммутативно, т. е. 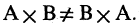
Пример:
Пусть А — отрезок [1,3], В — отрезок [2,5]. Тогда 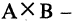 множество точек прямоугольника, заштрихованного на рис. 1.6,
множество точек прямоугольника, заштрихованного на рис. 1.6, 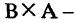 прямоугольник, заштрихованный на рис. 1.7.
прямоугольник, заштрихованный на рис. 1.7.
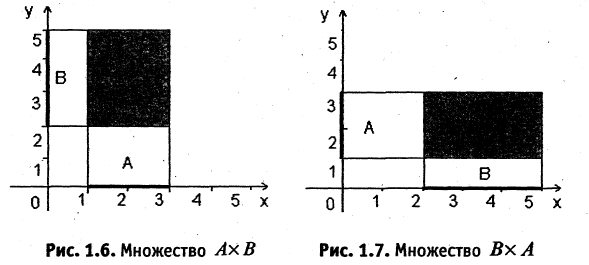
Пример:
Пусть А — множество, элементами которого являются буквы, цифры и все знаки операций и препинания. Такое множество называют алфавитом. Тогда  множество всех слов длины
множество всех слов длины  .
.
Природа компонентов прямого произведения обычно отличается от природы элементов сомножителей. Например, пусть Q — множество участников шахматного турнира, тогда  при всех
при всех  есть множество пар участников, причем
есть множество пар участников, причем 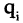 играет белыми фигурами,
играет белыми фигурами, 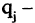 черными.
черными.
Понятие соответствия
Пусть заданы два множества  . Если для каждого элемента
. Если для каждого элемента 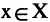 указан элемент
указан элемент 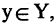 с которым сопоставляется
с которым сопоставляется 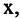 то говорят, что между множествами
то говорят, что между множествами 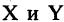 установлено соответствие. Иначе говоря, соответствием называется тройка множеств
установлено соответствие. Иначе говоря, соответствием называется тройка множеств  Множество
Множество 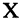 называется областью отправления,
называется областью отправления, 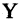 — областью прибытия,
— областью прибытия, 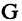 — графиком соответствия. Если
— графиком соответствия. Если 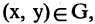 то множество первых проекций
то множество первых проекций 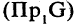 называется областью определения соответствия, множество вторых проекций
называется областью определения соответствия, множество вторых проекций 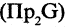 — областью значений этого соответствия,
— областью значений этого соответствия, 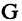 — график соответствия.
— график соответствия.
Два соответствия равны тогда и только тогда, когда равны их области отправления, области прибытия и графики. Пример. Заданы четыре разных соответствия, имеющие одинаковые области отправления и прибытия:
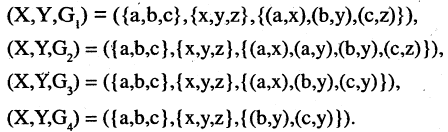
На рис. 1.8а, 1.86, 1.8в, и 1.8г. различия этих соответствий видны достаточно наглядно.
В соответствии  множество всех
множество всех  которые сопоставляются элементу
которые сопоставляются элементу 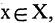 называется образом
называется образом 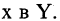 Множество же всех
Множество же всех 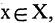 которым сопоставляют элемент
которым сопоставляют элемент 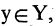 называется прообразом
называется прообразом 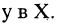
Соответствие называется всюду определенным, если множество 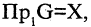 т. е. его область определения, совпадает с областью отправления (в противном случае говорят о частичном соответствии). Если же
т. е. его область определения, совпадает с областью отправления (в противном случае говорят о частичном соответствии). Если же 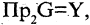 то соответствие называют сюръективным, или накрывающим. Это означает, что область значений соответствия совпадает с его областью прибытия. На рис. 1.8 а и 1.8 б представлено всюду определенное сюръективное соответствие. Соответствия, представленные на рис.18 в и 1.8 г, не сюръективны, а соответствие, изображенное на рис. 1.8, г не всюду определенное.
то соответствие называют сюръективным, или накрывающим. Это означает, что область значений соответствия совпадает с его областью прибытия. На рис. 1.8 а и 1.8 б представлено всюду определенное сюръективное соответствие. Соответствия, представленные на рис.18 в и 1.8 г, не сюръективны, а соответствие, изображенное на рис. 1.8, г не всюду определенное.
Соответствие 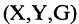 называется функциональным (или однозначным), если образом любого элемента из
называется функциональным (или однозначным), если образом любого элемента из 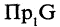 является единственный элемент из
является единственный элемент из 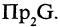 График такого соответствия называется функциональным. Это означает, что в нем нет пар с одинаковыми первыми и различными вторыми компонентами. Например, соответствие, представленное на рис. 1.8 б, нефункционально. Соответствие называется инъективным, если любому элементу из
График такого соответствия называется функциональным. Это означает, что в нем нет пар с одинаковыми первыми и различными вторыми компонентами. Например, соответствие, представленное на рис. 1.8 б, нефункционально. Соответствие называется инъективным, если любому элементу из 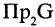 соответствует единственный элемент из
соответствует единственный элемент из 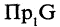 , на рис. 1.8 в изображено инъективное соответствие.
, на рис. 1.8 в изображено инъективное соответствие.
Соответствие между 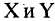 называется взаимно-однозначным (или биективным), если оно всюду определено, сюръективно, функционально и инъективно.
называется взаимно-однозначным (или биективным), если оно всюду определено, сюръективно, функционально и инъективно.
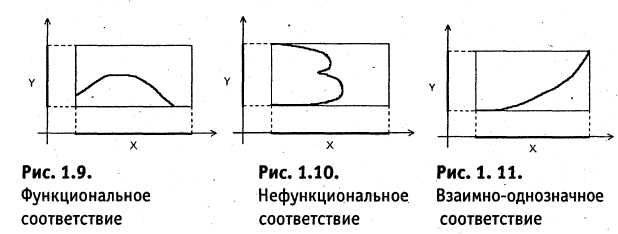
Пусть 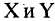 — множества вещественных чисел. В этом случае график соответствия
— множества вещественных чисел. В этом случае график соответствия  может быть представлен некоторой линией на плоскости. Например. На рис. 1.9 представлено функциональное соответствие, но оно не инъективно (некоторым
может быть представлен некоторой линией на плоскости. Например. На рис. 1.9 представлено функциональное соответствие, но оно не инъективно (некоторым 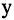 соответствует более одного
соответствует более одного 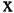 ), не всюду определено (
), не всюду определено ( определен не для всех
определен не для всех 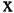 ), не сюръективно (
), не сюръективно ( проектируется не на все
проектируется не на все 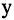 ) и не биективно. На рис. 1.10 представлено нефункциональное соответствие, которое не всюду определено, сюръективно и не биективно. На рис. 1.11 представлено взаимно-однозначное соответствие.
) и не биективно. На рис. 1.10 представлено нефункциональное соответствие, которое не всюду определено, сюръективно и не биективно. На рис. 1.11 представлено взаимно-однозначное соответствие.
Мощность множества
Мощность множества характеризует количество элементов этого множества. Множества равномощны, если между их элементами можно установить взаимно-однозначное соответствие. Число элементов в конечном множестве А называется кардинальным числом и обозначается |А|. Подсчет элементов конечного множества заключается в установлении взаимно-однозначного соответствия между этими элементами и конечной последовательностью натуральных чисел.
Множество называется бесконечным, если оно равномощно хотя бы одному из его собственных подмножеств. Бесконечное множество А называется счетным, если оно равномощно множеству всех натуральных чисел N. Примеры счетных множеств: множество целых чисел, четных чисел, рациональных чисел. Счетное множество образуется при объединении счетного множества конечных множеств (например, множество слов в любом конечном алфавите) и т. д. Счетным будет и объединение счетного множества счетных множеств (множество всех векторов с натуральными компонентами). Множество А называется не более чем счетным, дискретным, если оно конечно (в частности, пусто) или счетно. Счетное множество среди бесконечных множеств имеет наименьшую мощность.
Рассмотрим все вещественные числа на отрезке 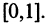 Эти числа не могут быть пронумерованы, следовательно, их множество не образует счетное множество, оно несчетно. По определению, множество, равномощное множеству всех вещественных чисел
Эти числа не могут быть пронумерованы, следовательно, их множество не образует счетное множество, оно несчетно. По определению, множество, равномощное множеству всех вещественных чисел
единичного отрезка числовой оси, имеет мощность континуума (непрерывное множество). Мощность множества континуума превышает мощность счетного множества. Любой конечный отрезок числовой оси равномощен единичному отрезку. Более того, любой конечный отрезок равномощен и всей числовой оси. Например, между отрезком 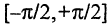 и множеством
и множеством 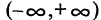 можно установить такое соответствие:
можно установить такое соответствие: 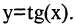
Множества наибольшей мощности не существует. Это следует из того, что мощность любого множества А всегда строго меньше мощности множества всех его подмножеств 
Множества — основные понятия
Под множеством понимается совокупность каких-либо объектов, называемых элементами этого множества. Например, можно говорить о множестве студентов данного вуза, множестве учебников по математике, множестве треугольников, множестве действительных чисел и т. д. Множества, содержащие конечное число элементов, называются конечными (множество студентов, множество учебников). Множества с бесконечным числом элементов называются бесконечными (множество треугольников, множество действительных чисел).
Множество обычно обозначается заглавными латинскими буквами A, B, С, …, а их элементы — малыми а, b, с, ….
Утверждение ’’элемент х принадлежит множеству А” записывается так : «х ∈ А ”, а противоположное утверждение ” элемент х не принадлежит множеству А” записывается так : ”х ∉ А ”.
Определение:
Если все элементы множества А принадлежат также множеству В, то говорят, что ” А содержится в В” или: ” А является подмножеством В”, и записывают так: A ⊂ В.
Определение:
Два множества называются равными (совпадающими), если они состоят из одних и тех же элементов: A = B.
Пример:
Сформулируйте словами утверждение:
A=B⇔ A ⊂ B и B ⊂ A и докажите его.
Конечное множество можно задать перечислением его элементов. Так, запись A = {1;2;3} означает, что множество А состоит из трех чисел 1,2,3. При этом порядок перечисления элементов не играет роли: {1;2;3} = {3;2;1}.
Бесконечное множество можно задать, написав условие, которое выполняется для всех элементов данного множества и не выполняется для других. Запись
В = {x | 1 < х < 2}
означает множество всех чисел, больших одного, но меньших двух, т.е. интервал (1;2).
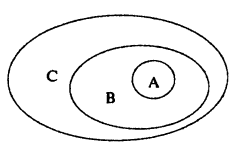
Множество удобно схематически изображать в виде ’’диаграмм Эйлера” — геометрических фигур на плоскости, взаимное расположение которых отражает отношение между множествами. Так, например, если A ⊂ B и B ⊂ C, то A изображается частью В₁ а В частью C (рис. 1). C помощью диаграммы Эйлера на рис. 1 наглядно видно свойство транзитивности операции включения множеств: A ⊂ B ⊂ C ⟹ A ⊂ C.
Определение:
Множество называется пустым, если оно не содержит ни одного элемента. Пустое множество обозначается символом ⊘.
Так, например, множество отрицательных натуральных чисел пусто.
Операции над множествами
Определение:
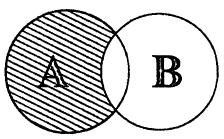
Пересечением множеств A и B называется множество С, состоящее из всех элементов, одновременно входящих и в А, и в В. Это записывается следующим образом: A ∩ В = С.
Иллюстрация пересечения двух множеств с помощью диаграмм Эйлера приведена на рис. 2, где множество C заштриховано.
Пример:
Если множество А есть интервал (1 ;5) а множество В есть интервал (2;7), то пересечение множеств A и B есть интервал (2;5).
Свойства операции пересечения множеств приведем без доказательств:
- A ∩ В = В ∩ А(коммутативность).
- A ∩ (В ∩ С) = (A ∩ В) ∩ C = A ∩ В ∩ С(ассоциативность).
- A ⊂ В ⟹ А ∩ В = А.
- A∩A= А.
- A ∩ ⊘ = ⊘
Определение:
Объединением множеств A и B называется множество С, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств или А, или В, или A u B одновременно. Это обозначается следующим образом : A ∪ В = С.
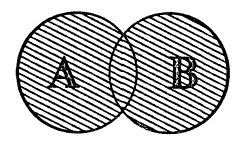
Иллюстрация объединения с использованием диаграмм Эйлера приведена на рис. 3, где множество C заштриховано.
Пример:
Если множество А есть отрезок [1;3], множество В есть отрезок [2;5], то A ∪ B есть отрезок B=[1;5].
Свойства операции объединения множеств приведем без доказательств:
1) A ∪ B=B ∪ A (коммутативность).
2) A ∪ (B∪C)=(A ∪ B) ∪ C=A ∪ B ∪ C (ассоциативность).
3) A∩(B∪C)=(A∩B) ∪ (A∩C) (дистрибутивность).
4) A ⊂ B ⇒A ∪ B=B.
5) A ∪ A=A.
6) A ∪ ⊘=A.
Определение:
Разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих В. Разность A u B обозначается АВ и изображена штриховкой на рис. 4.
Операция вычитания множеств не коммутативна : A∖B≠B∖A.
Пример:
Если А = (1; 10), В = (3; 20), то АВ=(1;3], ВА =[10,20).
Кванторы общности и существования
При изложении материала мы будем использовать знак  , называемый квантором общности, и знак Ǝ, называемый квантором существования. Символ
, называемый квантором общности, и знак Ǝ, называемый квантором существования. Символ 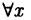 означает: ’’для любого х«, ’’для всех х”, ’’для каждого х«, ’’какое бы ни было х«. Запись
означает: ’’для любого х«, ’’для всех х”, ’’для каждого х«, ’’какое бы ни было х«. Запись 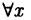 > 0 означает: ’’для всех положительных x” Запись
> 0 означает: ’’для всех положительных x” Запись 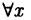 ∈ M читается: ’’для всех x, принадлежащих множеству М”.
∈ M читается: ’’для всех x, принадлежащих множеству М”.
Обозначение Ǝх означает: ’’существует такое х, что …”, ”по крайней мере для одного х…”, запись Ǝх > 0 читается: ’’существует такое положительное число х, что…”, запись Ǝх₁ ,x₂ Є M означает: ’’существуют такие х₁ ,x₂ — элементы множества М, что …”.
Нам также неоднократно придется использовать символы ⇒ и ⇔.
Запись логического следования А ⇒ В означает, что если верно утверждение А, то верно и утверждение В, то-есть из А следует В.
Запись логической равносильности ⇔ означает, что из А следует В и наоборот, из В следует А.
Так, например, запись: 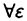 > ƎN
> ƎN 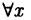 > N ⇒ | f (x) — b| < ε читается следующим образом: ’’для любого ε больше 0 существует N такое, что для любых х, больших N, будет выполняться неравенство | f (x) — b∣< ε.”
> N ⇒ | f (x) — b| < ε читается следующим образом: ’’для любого ε больше 0 существует N такое, что для любых х, больших N, будет выполняться неравенство | f (x) — b∣< ε.”
Необходимое и достаточное условие
Любая теорема может быть сформулирована в виде: если выполняется условие А, то верно утверждение В. Будем называть это прямой теоремой и схематически запишем в виде:
Теорема:
А ⇒ В.
В качестве примера приведем теорему, называемую достаточным условием экстремума непрерывной функции, изучаемую в курсе математики средней школы.
Теорема:
Если функция f непрерывна в точке а и производная f меняет знак при переходе через эту точку, то а является точкой экстремума функции f.
Условие А стоит после слова «если», утверждение В написано после
слова «то».
Определение:
А называется достаточным условием для
выполнения В. В свою очередь, В является необходимым условием для выполнения А.
Применительно к теореме 1.2 это выглядит следующим образом.
Достаточным условием для существования экстремума непрерывной функции f в точке а является изменение знака ее производной при переходе через эту точку.
Для лучшего усвоения введенных понятий рассмотрим очевидно справедливое утверждение не из области математики.
Теорема:
Если человек здоров, то у него есть голова.
Здесь здоровье является достаточным условием наличия у человека головы. Наоборот, наличие головы является необходимым условием здоровья. Подумайте, будет ли это условие достаточным для того, чтобы человек был здоров? Реально ли вообще сформулировать достаточное условие того, что человек здоров?
Обозначим А утверждение, заключающееся в отрицании утверждения А(читается «не А»). Если справедлива прямая теорема 1.1, то методом «от противного» легко можно доказать справедливость следующего утверждения, которое называется
«противоположная к обратной теорема»:
Теорема:
В ⇒ А.
Доказательство:
Имеем А ⇒ В, нужно доказать, что В⇒ А Предположим противное: В ⇒ А, но в соответствии с теоремой 1.1 А ⇒ В. Полученное противоречие (В ⇒ В) доказывает теорему.
Аналогично можно доказать, что если справедлива теорема 1.4, то верна теорема 1.1, т. е. эти утверждения равносильны.
Для теоремы 1.2 противоположной к обратной будет теорема: ’’Если точка а не является точкой экстремума функции f ̕ непрерывной в этой точке, то производная f ̕ не меняет знак при переходе через эту точку”.
Для теоремы 1.3 противоположным к обратному будет утверждение: ’’Если у человека нет головы, то он не здоров”.
Проведите доказательство этого утверждения самостоятельно методом ”от противного».
Наряду с прямой теоремой 1.1 можно рассмотреть утверждение, называемое «обратной теоремой” :
Теорема:
В ⇒ А.
Однако обратная теорема не всегда справедлива, если верна прямая. Так, например, для теоремы 1.3 обратное утверждение: «Если у человека есть голова, то он здоров”, очевидно, не верно.
Если все же теорема 1.5 справедлива, то методом «от противного” исходя из нее доказывается справедливость утверждения, называемого «противоположная теорема”:
Теорема:
А ⇒ В
Наоборот, из теоремы 1.6 вытекает справедливость теоремы 1.5, т.е. эти утверждения равносильны. Заметим, что из прямой теоремы 1.1 не обязательно следует справедливость противоположной теоремы 1.6.
Приведенные связи удобно запоминать, представляя себе следующий ’’логический квадрат» (рис. 5):
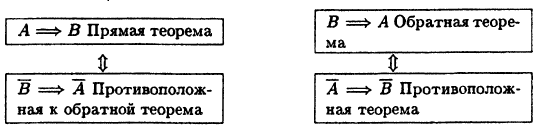
Если наряду с прямой теоремой выполняется также обратная теорема, то А является ’’необходимым и достаточным” условием для В. То же самое можно сказать про В по отношению к А.
Так, например, то, что треугольник прямоугольный, является необходимым и достаточным условием того, что квадрат одной из сторон равен сумме квадратов двух других.
Множество N натуральных чисел
Определение:
Числа 1,2,3,… называются натуральными.
Сумма и произведение натуральных чисел будет числом натуральным, а разность и частное — не всегда. При вычитании натуральных чисел может получится отрицательное число, а при делении — не целое. Например, при делении 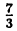 получится целая часть 2 и 1 в остатке, что записывается следующим равенством:
получится целая часть 2 и 1 в остатке, что записывается следующим равенством: 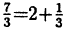 .
.
Приводя к общему знаменателю, получим равенство: 7 = 2 ∙ 3 + 1. В этих равенствах 7 называется делимым, 3 — делителем, 2 — целой частью и 1 — остатком (остаток всегда меньше делителя). Если остаток равен нулю, то говорят, что делимое делится на делитель, как, например, 6 делится на 3. Если натуральное число, большее единицы, делится только на 1 и на себя (что всегда справедливо), то оно называется простым. Простыми числами являются числа 2,3,5,7,11,13,17,19,23 и т. д. Любое натуральное число может быть представлено в виде произведения простых сомножителей. Например : 12 = 1 ∙ 2 2 3, 18 = 1 2 ∙ 3 3, 7 = 1 ∙ 7 и т. д.
Определение:
Наименьшим общим кратным двух данных натуральных чисел называется наименьшее из чисел, которые делятся на каждое из них.
Для любых двух натуральных чисел всегда найдется наименьшее общее кратное, поскольку их произведение всегда делится на каждое из двух данных.
Наименьшее общее кратное 12 и 18 равно 36. Для того чтобы найти наименьшее общее кратное двух чисел, нужно первое число помножить на простые множители, входящие в разложение второго числа и не входящие в разложение первого: 12 ∙ 3 = 36.
Определение:
Наибольшим общим делителем двух данных натуральных чисел называется наибольшее из чисел, на которые делится каждое из них.
Для любых двух натуральных чисел всегда найдется наибольший общий делитель, поскольку любые два числа всегда делятся на единицу. Если у двух натуральных чисел нет других общих делителей кроме единицы, они называются взаимно простыми. Наибольший общий делитель 12 и 18 равен 6. Для того, чтобы найти наибольший общий делитель двух чисел, нужно перемножить общие простые множители, входящие в разложение и одного, и другого числа: 1 ∙ 2 ∙ 3 = 6.
Множество Z целых чисел
Определение:
Натуральные, отрицательные натуральные числа и ноль образуют множество целых чисел (множество Z).
Сумма, произведение и разность целых чисел является целым числом, а частное — не всегда. Иногда множество отрицательных целых чисел обозначается Z_.
Множество натуральных чисел является подмножеством множества целых чисел: N ⊂ Z.
Множество Q рациональных чисел
Определение:
Рациональными числами называются числа вида 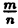 , где m — целое (m Є Z), n — натуральное (n Є N), тип взаимно простые. Множество рациональных чисел обозначается Q.
, где m — целое (m Є Z), n — натуральное (n Є N), тип взаимно простые. Множество рациональных чисел обозначается Q.
Множество целых чисел является подмножеством множества рациональных чисел, т. к. любое целое число m можно рассматривать как рациональное, представив в виде 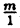 . Сумма, произведение, разность, частное рациональных чисел ( при ненулевом знаменателе) является числом рациональным, однако корень из рационального числа — не всегда, как, например,
. Сумма, произведение, разность, частное рациональных чисел ( при ненулевом знаменателе) является числом рациональным, однако корень из рационального числа — не всегда, как, например, 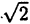 ,
,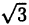 и т.д.
и т.д.
Всякое рациональное число 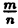 можно представить в виде десятичной дроби, конечной или периодической. И наоборот, любая конечная или периодическая десятичная дробь может быть записана в виде простой дроби.
можно представить в виде десятичной дроби, конечной или периодической. И наоборот, любая конечная или периодическая десятичная дробь может быть записана в виде простой дроби.
Пример:
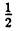 =0,5;
=0,5; 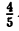 =0,8 ;
=0,8 ; 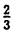 =0,666…=0,(6) ;
=0,666…=0,(6) ; 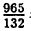 =7,31(06).
=7,31(06).
Две последние десятичные дроби бесконечные периодические. Повторяющиеся цифры называются периодом дроби и пишутся в скобках, количество этих цифр называется длиной периода. Для обратного преобразования конечной десятичной дроби ее нужно представить в виде простой и сократить: 0,8=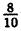 =
=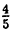 . На самом деле разница между конечной дробью и периодической непринципиальная. Так, 0,5=0,4(9).
. На самом деле разница между конечной дробью и периодической непринципиальная. Так, 0,5=0,4(9).
Перевод периодической десятичной дроби в простую объясним на примере.
Пример:
Записать в виде простой дроби 0,(6).
Решение:
Периодическую дробь 0,(6) обозначим за x: 0,(6)=x, тогда, т. к. 10‧х — 10-0,666… = 6,666…, легко заметить, что 10∙х = 6 х. Решая это уравнение, получаем: 9‧x=6⇔x =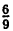 =
= 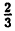 .
.
Определение:
Целой частью числа называется наибольшее целое число, не превосходящее данное. Целая часть числа х обозначается [x].
Примеры:
[3,56]=3; [0,12]=0; [-0,12]=-1; [-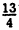 ]=-4;
]=-4;
[5]=5; [0]=0.
Определение:
Дробной частью числа называется разность между самим числом и его целой частью. Дробная часть числа обозначается {x}. Она строго меньше единицы и находится в пределах : 0 ≤ {x} < 1.
Примеры:
{3,56}=0,56; {0,12}=0,12; {-0,12}=0,88;
{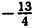 }=
}=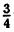 ; {5}=0; {0}=0.
; {5}=0; {0}=0.
Множество J иррациональных чисел
Определение:
Иррациональным числом называется бесконечная непериодическая десятичная дробь.
Примерами иррациональных чисел являются √2, √3, ∛11, π, е, и т. д. Заметим, что J ∩Q = ⊘ Иррациональное число нельзя представить в виде простой дроби, его также невозможно ’’выписать до конца” (представить в виде конечной десятичной дроби), поэтому запись √2 = 1,41 ошибочна, следует писать √2 ≈ 1,41.
Заданное бесконечной непериодической дробью иррациональное число определяет две последовательности конечных (рациональных) десятичных дробей, называемых десятичными приближениями по недостатку и по избытку. Например, для √2 можно написать:
1 √2<2,
1,4< √2<1,5,
1,41< √2<1,42.
…
В инженерных расчетах при замене иррациональных чисел их рациональными приближениями достаточно во всех вычислениях брать на один знак больше, чем требуется в результате, и затем округлить результат.
Для иррациональных чисел можно также определить целую и дробную части, причем для х ∈ J ⇒ {τ} ∈ J.
Множество R действительных чисел
Определение:
Все рациональные и иррациональные числа образуют множество действительных (вещественных) чисел: R = QuJ.
В множестве действительных чисел всегда выполнимы сложение, вычитание, умножение, деление (не на ноль), возведение в любую действительную степень положительного числа, извлечение корня нечетной степени из отрицательного числа.
В множестве действительных чисел невозможно извлечение корня четной степени из отрицательного числа.
Числовая ось
Множеству действительных чисел можно дать простую геометрическую интерпретацию. Выберем на прямой положительное направление (указывается стрелкой), начало отсчета и единицу масштаба. Такая прямая называется числовой осью. Каждой ее точке можно поставить в соответствие единственное действительное число следующим образом: положительное число х изображается точкой, расположенной на оси на расстоянии х в направлении стрелки (на рис. 6 справа от О), отрицательное с другой стороны (на рис. 6 слева от О) на расстоянии х от О.
Число х называется координатой соответствующей точки на числовой оси. Из двух чисел больше будет то, которое расположено на числовой оси дальше в направлении стрелки (на рис. 6 — правее).

Например, -1 > -2.
Числовые промежутки
Если известны два действительных числа а и b, a < b, то можно определить следующие множества действительных чисел, находящихся между двумя данными — числовые промежутки.
Отрезок (сегмент) [α; b]= {x | a ≤ х ≤ b},
Интервал (a; b)= {x | a < х < b}.
В частности, можно рассматривать бесконечные интервалы:
(- ∞; +∞)={x∈R}, (a;+∞)={x|x>a}, (- ∞ ;b)={x|x<b}.
Полуинтервал, [a;b)={x∣a≤x<b}, (a;b]={x∣a<x≤b}.
В частности, можно рассматривать бесконечные полуинтервалы: [a;+∞)={x∣x≥a}, (-∞;b]={x∣x≤b}.
Числовые промежутки изображают на числовой оси, причем если граничная точка принадлежит промежутку — она закрашена, если нет — изображается светлым кружком (’’выкалывается”). На рис 7 изображен полуинтервал (2;5].

Числовые промежутки будем выделять штриховкой или утолщенной линией.
Примеры с решением на тему: «Множества«
При решении примеров данного практического занятия используется материал средней школы и материал лекции 1. Применение метода интервалов для решения неравенств иллюстрируется примерами 1.2-1.5
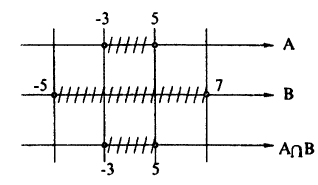
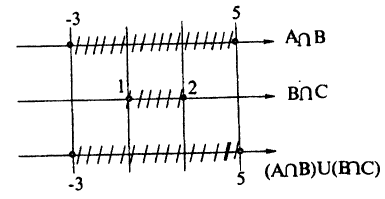
Пример:
Пусть A = [-3;5],B = (-5;7),C = [1;2). Найдите множество: A₀ = (4 ∩ В) U (В ∩ С).
Решение:
Для нахождения результата операций над числовыми промежутками их удобно изображать на числовых осях, расположенных одна под другой с согласованным началом и одинаковым масштабом. Если исходные промежутки А и В заштриховать, то их пересечением будет множество точек, заштрихованных на каждой из осей (рис. 8), а их объединением — множество точек, заштрихованных хотя бы на одной из осей (рис. 9).
Пользуясь этим правилом, последовательно получим A ∩ В, В ∩C и, наконец, (Л ∩ В) ∪ (В ∩ С) (рис. 8, 10, 11).
Ответ: A₀ ≈ [-3; 5].
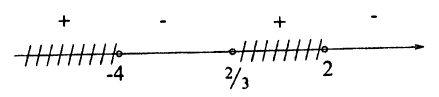
Пример:
Найдите элементы множества:
A₀ = {x | (2 — 3x)(x + 4)(x — 2) > 0}.
Решение:
Неравенство (2 — 3x)(х + 4)(x — 2) > 0 решим методом интервалов, для чего нанесем на числовую ось значения х, при которых левая часть неравенства обращается в ноль: x₁ =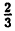 ,x₂ = -4,х₃ = 2. (рис. 12)
,x₂ = -4,х₃ = 2. (рис. 12)
Сами эти значения не удовлетворяют неравенству, поэтому соответствующие точки “выколоты».
Знаки выражения в левой части неравенства определим, подставляя в него по одному значению из каждого интервала, на которые все множество R разбилось точками x₁,x₂,х₃. Отметим штриховкой те интервалы, на которых выражение в левой части неравенства положительно. Это множество является искомым.
Ответ: A₀=(-∞; -4) ∪ (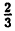 ; 2).
; 2).
Пример:
Задайте характеристическим свойством множество: A₀ — множество всех натуральных чисел, меньших 5 или больших 10.
Решение:
В условии требуется,чтобы натуральные числа были меньше 5 или больше 10, т.е. искомое множество есть объединение двух подмножеств: множества натуральных чисел, меньших 5 и больших 10.
Ответ: A₀ = {x|x < 5, х ∈ N} ∪ {x|x > 10, х ∈ N}.
Пример:
Решите систему неравенств: 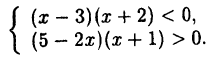
Решение:
Решение системы неравенств есть пересечение множеств решений каждого из входящих в систему неравенств. Аналогично тому, как это делалось при решении примера 1.2, решим каждое из неравенств системы методом интервалов и найдем их пересечение (рис 13).
Ответ: х ∈ (-1; 2,5).
Пример:
Решите совокупность систем неравенств: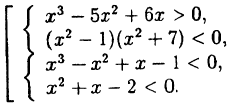
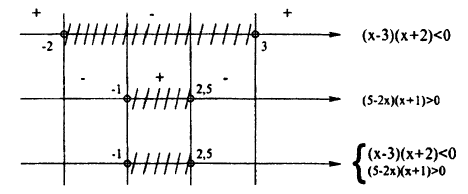
Решение:
Решение совокупности систем неравенств есть объединение решений каждой системы, входящей в совокупность. Для решения разложим каждый многочлен в произведение с помощью корней: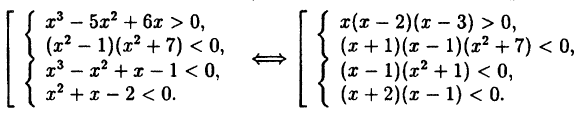
Решение совокупности систем методом интервалов представлено на рис. 14
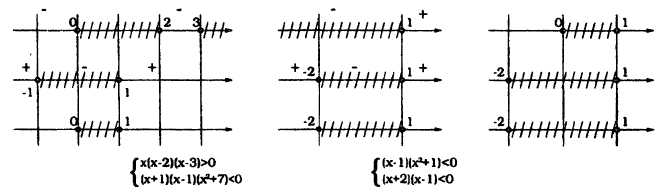
Ответ: х ∈ (-2; 1)
Множества
Понятие множества является одним из основных понятий математики. Оно не сводится к другим понятиям и не определяется. Вместо определения приводят лишь примеры, поясняющие его смысл. Так, можно говорить о множестве всех учеников данной школы, о множестве всех собак на земном шаре, о множестве всех клеток данного человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех натуральных чисел, о множестве всех треугольников на данной плоскости, о множестве всех точек данного круга и т. д.
Когда в математике говорят о множестве, то объединяют некоторые предметы в одно целое — множество, состоящее из этих предметов. Основатель теории множеств Георг Кантор (1845—1918) выразил это следующими словами: «Множество есть многое, мыслимое как единое».
Предметы (объекты), составляющие некоторое множество, называются его элементами. То обстоятельство, что объект а является элементом множества А, записывается так: 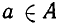 (словами: а есть элемент множества А; а принадлежит А; а содержится в А; А содержит а). Если объект а не является элементом множества А, то это записывается так:
(словами: а есть элемент множества А; а принадлежит А; а содержится в А; А содержит а). Если объект а не является элементом множества А, то это записывается так: 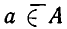 (словами: а не есть элемент множества А; а не принадлежит А; а не содержится в А; А не содержит а).
(словами: а не есть элемент множества А; а не принадлежит А; а не содержится в А; А не содержит а).
Например, если А есть множество всех четных натуральных чисел, то 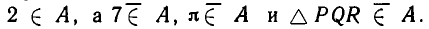
Множество иногда можно задать перечислением всех его элементов. В этом случае употребляют фигурные скобки, в которые помещают названия всех элементов множества, разделенные запятыми. Так, {1, 2, 3) обозначает множество, состоящее из чисел «один», «два», «три» и только из них.
Вообще некоторое множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характеристическим свойством множества.
Характеристическим свойством множества {1, 2, 3) может быть свойство совпадать с одним из членов списка, приведенного в фигурных скобках. Другим характеристическим свойством этого же множества является свойство быть корнем уравнения
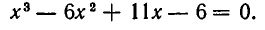
Числовые множества
Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, числа, уравнения, точки, углы и т. д. Именно этим объясняется чрезвычайная широта теории множеств и ее приложимость к самым разным областям знания (математике, механике, физике, лингвистике, экономике и т. д.). Для математики особо важную роль играют множества, составленные из «математических» объектов— корней уравнений, геометрических фигур и т. д. Чаще всего нам будут встречаться числовые множества, то есть множества, элементами которых являются числа. Примерами числовых множеств являются: а) множество всех действительных чисел; б) множество всех рациональных чисел; в) множество всех положительных чисел; г) множество всех чисел, удовлетворяющих неравенству 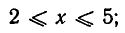 д) множество всех чисел вида
д) множество всех чисел вида 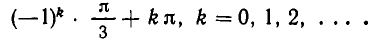
Некоторые числовые множества имеют особые названия. Если даны два числа а и b, а < b, то множество всех чисел, удовлетворяющих неравенству 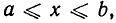 называют числовым отрезком или,
называют числовым отрезком или,
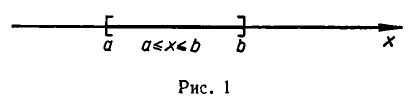
если это не вызывает недоразумений, просто отрезком и обозначают [а, b]. На числовой оси ему соответствует отрезок с концами а и b (рис. 1).
Множество чисел, удовлетворяющих неравенству а < х< b , называют числовым промежутком или, короче, промежутком и обозначают (а, b). На числовой оси ему соответствует отрезок, у которого отброшены концевые точки (рис. 2).
Множество чисел, удовлетворяющих неравенствам вида х > а (или х<а), называют (числовым) лучом. Его обозначают (а,  )
)
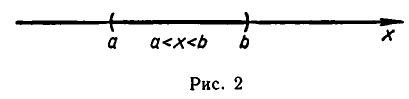
(или (— , а)) (рис. 3). Иногда нам будут встречаться множества чисел, удовлетворяющих неравенствам
, а)) (рис. 3). Иногда нам будут встречаться множества чисел, удовлетворяющих неравенствам 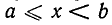 или
или 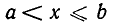 (рис. 4). Их называют (числовыми) полуотрезками и обозначают [а, b) и (а, b]. Заметим, что квадратная скобка означает, что соответствующий
(рис. 4). Их называют (числовыми) полуотрезками и обозначают [а, b) и (а, b]. Заметим, что квадратная скобка означает, что соответствующий
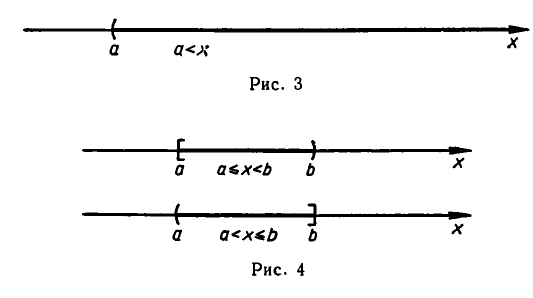
конец включается в множество, а круглая — что он исключается.
Пустое множество
Введение понятия множества в математику оказалось очень полезным. Из-за того что элементами множеств могут быть вещи самой различной природы, одни и те же утверждения, касающиеся множеств, можно истолковать и как утверждения о натуральных числах, и как утверждения о точках геометрических фигур, и как утверждения о множестве слов и т. д. Таким образом, понятия и теоремы теории множеств обладают большой общностью. Этим и объясняется то, что язык теории множеств применяется в самых различных областях математики.
В математике приходится иногда рассматривать множества, содержащие только один элемент, и даже множества, не имеющие ни одного элемента. Множество, не содержащее ни одного элемента, называют пустым. Его обозначают знаком 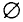 . На первый взгляд может показаться, что понятие пустого множества излишне. Но когда множество задано своим характеристическим свойством, заранее неизвестно, пусто оно или нет. Например, пусть некоторое множество состоит из всех прямоугольников с неравными диагоналями. То, что свойство «быть прямоугольником с неравными диагоналями» задает пустое множество, составляет утверждение геометрической теоремы: «Во всяком прямоугольнике диагонали равны». Точно так же из теоремы Пифагора следует, что множество прямоугольных треугольников, для которых квадрат гипотенузы не равен сумме квадратов катетов, пусто. Вот еще несколько примеров задания пустого множества характеристическим свойством: а) множество рациональных чисел r таких, что
. На первый взгляд может показаться, что понятие пустого множества излишне. Но когда множество задано своим характеристическим свойством, заранее неизвестно, пусто оно или нет. Например, пусть некоторое множество состоит из всех прямоугольников с неравными диагоналями. То, что свойство «быть прямоугольником с неравными диагоналями» задает пустое множество, составляет утверждение геометрической теоремы: «Во всяком прямоугольнике диагонали равны». Точно так же из теоремы Пифагора следует, что множество прямоугольных треугольников, для которых квадрат гипотенузы не равен сумме квадратов катетов, пусто. Вот еще несколько примеров задания пустого множества характеристическим свойством: а) множество рациональных чисел r таких, что 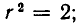 б) множество всех точек пересечения двух параллельных прямых; в) множество треугольников, сумма углов которых отлична от 180°; г) множество квадратных уравнений, имеющих более двух раз личных корней; д) множество решений системы уравнений
б) множество всех точек пересечения двух параллельных прямых; в) множество треугольников, сумма углов которых отлична от 180°; г) множество квадратных уравнений, имеющих более двух раз личных корней; д) множество решений системы уравнений
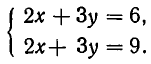
О некотором множестве может быть неизвестно, является ли оно пустым множеством или нет. Так, до сих пор неизвестно, пусто ли множество натуральных чисел n таких, что n > 2, а уравнение 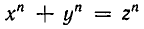
имеет положительные целочисленные решения (в этом состоит известная проблема Ферма).
Пустое множество единственно: нет двух разных пустых множеств.
Подмножество
Пусть даны два множества A и B, причем каждый элемент первого множества является элементом второго множества. Тогда множество А называют подмножеством (или частью) множества В. В этом случае пишут: 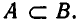
Примеры подмножеств: а) числовой отрезок [1,3] есть подмножество числового отрезка [0, 4];
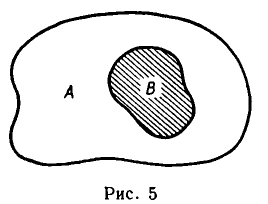
б) множество всех квадратов есть подмножество множества всех прямоугольников; в) множество всех целых чисел есть подмножество множества всех рациональных чисел.
Отметим, что пустое множество 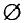 является подмножеством любого множества А. Каждое множество А является одним из своих подмножеств. Эти два подмножества ( 0 и все множество) называют несобственными. Все остальные подмножества называют собственными.
является подмножеством любого множества А. Каждое множество А является одним из своих подмножеств. Эти два подмножества ( 0 и все множество) называют несобственными. Все остальные подмножества называют собственными.
Множества часто изображают наглядно как множество точек геометрической фигуры. Тогда подмножество — это множество то чек части фигуры (рис. 5).
Пересечение множеств
Пусть даны множества А, В, С, … . Их пересечением называют множество X, содержащее те и только те элементы, которые входят в каждое из заданных множеств. Пере сечение двух множеств А и В обозначают АВ или 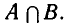
Если множества А и В состоят из точек некоторых геометрических фигур, то 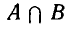 — множество общих точек этих фигур, то есть множество точек пересечения этих фигур в обычном смысле (рис. 6).
— множество общих точек этих фигур, то есть множество точек пересечения этих фигур в обычном смысле (рис. 6).
Пересечение множеств называют также их произведением, а операцию пересечения — умножением множеств. Можно показать,
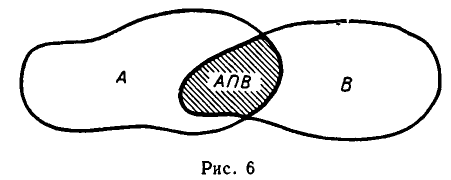
что многие свойства пересечения множеств напоминают свойства умножения чисел.
Примеры пересечения множеств: а) пересечением числового отрезка [0, 4 ] с числовым отрезком [2, 5] является числовой отрезок [2, 4] (рис. 7);
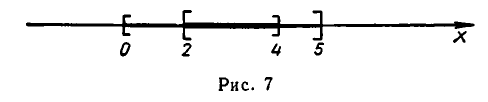
б) пересечение числового отрезка [0, 2] с числовым отрезком [3, 5] пусто; в) пересечение множества всех ромбов с множеством всех прямоугольников есть множество всех квадратов; г) пересечением множества четных натуральных чисел с множеством натуральных чисел, делящихся на 3, является множество натуральных чисел, делящихся на 6.
Сложение множеств
Суммой (или объединением) множеств А, В, С, . . . называют множество X, состоящее из тех и только тех элементов, которые входят хотя бы в одно из этих («слагаемых») множеств. Сумму двух множеств А и В обозначают А + В или 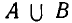 . Мы увидим позже, что некоторые свойства суммы множеств напоминают свойства суммы чисел.
. Мы увидим позже, что некоторые свойства суммы множеств напоминают свойства суммы чисел.
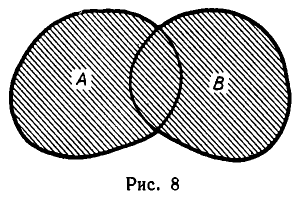
Если какой-нибудь элемент входит в несколько слагаемых множеств, то в сумме он берется лишь один раз. Например, суммой числового отрезка [0, 4] и числового отрезка [2, 5] является числовой отрезок [0, 5]. При этом точки отрезка [2, 4] входят в оба слагаемые, но в сумме они берутся лишь один раз. Впрочем, выражения «некоторый элемент берется в данном множестве пять раз» и т. п., как это следует из принятого нами понимания терминов «множество» и «элемент», просто не имеют смысла.
Примеры а) Обозначим через А множество точек некоторой плоской области и через В — множество точек другой области (рис. 8). Тогда их суммой будет множество точек заштрихованной фигуры, ограниченной на рис. 8 жирной линией. б) Обозначим через А множество успевающих учеников в классе, через В — множество девочек в этом классе и через С — множество неуспевающих мальчиков. Тогда 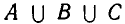 является множеством всех учеников этого класса. (Имеют ли множества А и В общие элементы?) в) Обозначим через
является множеством всех учеников этого класса. (Имеют ли множества А и В общие элементы?) в) Обозначим через 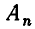 множество всех положительных дробей со знаменателем n. Тогда
множество всех положительных дробей со знаменателем n. Тогда 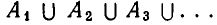 является множеством всех положительных дробей, то есть дробей вида
является множеством всех положительных дробей, то есть дробей вида 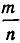 , где m и n — натуральные числа. г) Обозначим через
, где m и n — натуральные числа. г) Обозначим через 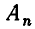 множество правильных n-угольников. Тогда
множество правильных n-угольников. Тогда 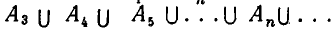 является множеством всех правильных многоугольников. д) Обозначим через A множество целых чисел вида 4n — 1, а через В — множество целых чисел вида 4n + 1. Тогда
является множеством всех правильных многоугольников. д) Обозначим через A множество целых чисел вида 4n — 1, а через В — множество целых чисел вида 4n + 1. Тогда 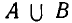 — множество всех нечетных целых чисел.
— множество всех нечетных целых чисел.
Разбиение множеств
Пусть множество X является суммой множеств A, В, С. . . , причем никакие два из них не имеют общих элементов. Тогда говорят, что множество X разбито на (непересекающиеся) подмножества А, В, С, . . . .
Примеры разбиения множеств: а) Множество натуральных чисел разбивается на подмножества четных чисел и нечетных чисел. б) Множество всех учеников в классе разбивается на множества учеников, фамилия которых начинается на букву «А», учеников, фамилия которых начинается на букву «Б», и т. д. вплоть до буквы «Я». Какое из этих множеств пусто, если взять ваш класс? Какие из этих множеств пусты для любого класса? в) Множество всех векторов на плоскости можно разбить на непересекающиеся подмножества, относя к одному подмножеству все векторы, равные друг другу по длине, параллельные и одинаково направленные. г) Это же множество можно разбить иначе, относя к одному под множеству векторы, выходящие из одной точки плоскости.
Вычитание множеств
Если даны два множества A и В, то их разностью называют такое множество X = A В или (А — В), в которое входят все элементы из Л, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества A. Таким образом, при вычитании множества В из множества A из A удаляют общую часть (пересечение) A и В:
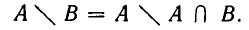
Например, если A — множество всех учащихся IX класса данной школы, а В — множество всех девочек, которые учатся в этой школе, то A В — множество всех мальчиков, обучающихся в IX классе этой школы.
В случае, когда В — часть множества А, А В называют дополнением к В в множестве А и обозначают 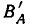 (разумеется, одно и то же множество В имеет разные дополнения в разных содержащих его множествах А). Например, дополнением множества четных чисел в множестве всех целых чисел является множество нечетных чисел. Дополнением множества всех квадратов в множестве прямоугольников является множество всех прямоугольников с неравными сторонами, а дополнением того же множества квадратов в множестве всех ромбов — множество ромбов с неравными диагоналями.
(разумеется, одно и то же множество В имеет разные дополнения в разных содержащих его множествах А). Например, дополнением множества четных чисел в множестве всех целых чисел является множество нечетных чисел. Дополнением множества всех квадратов в множестве прямоугольников является множество всех прямоугольников с неравными сторонами, а дополнением того же множества квадратов в множестве всех ромбов — множество ромбов с неравными диагоналями.
Отображение множеств
Пусть даны два множества X и У и пусть имеется правило  ставящее в соответствие каждому элементу
ставящее в соответствие каждому элементу 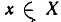 некоторый определенный
некоторый определенный 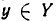 . Тогда говорят, что задано отображение
. Тогда говорят, что задано отображение 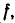 множества X в множество У. Элемент, соответствующий х в силу правила
множества X в множество У. Элемент, соответствующий х в силу правила 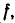 обозначают
обозначают 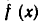 и пишут:
и пишут: 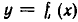 . Элемент у называют образом элемента х при отображении
. Элемент у называют образом элемента х при отображении 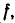 а элемент х называют прообразом элемента у при отображении
а элемент х называют прообразом элемента у при отображении 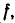 Отображение
Отображение 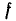 называют также функцией, заданной на множестве X и принимающей значения во множестве У. Множество X называют областью определения функции
называют также функцией, заданной на множестве X и принимающей значения во множестве У. Множество X называют областью определения функции 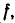
Если всякий 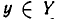 является образом некоторого
является образом некоторого 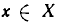 при отображении
при отображении 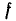 , то отображение
, то отображение 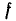 называют отображением множества X на множество У. В этом случае множество У называется областью значений функции
называют отображением множества X на множество У. В этом случае множество У называется областью значений функции 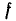 .
.
Приведем примеры отображений множеств: а) Пусть X — множество всех действительных чисел, У — множество всех неотрицательных чисел. Равенство 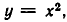 связывающее с элементом множества X элемент у множества У, задает отображение X на У. При этом числу 2 соответствует число 4, числу 6 — число 36 и т. д. б) Пусть X — множество всех действительных чисел, отличных от числа 3, У — множество всех действительных чисел. Равенство
связывающее с элементом множества X элемент у множества У, задает отображение X на У. При этом числу 2 соответствует число 4, числу 6 — число 36 и т. д. б) Пусть X — множество всех действительных чисел, отличных от числа 3, У — множество всех действительных чисел. Равенство 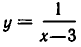 , связывающее с элементом х множества X элемент множества У, задает отображение X в У. Является ли это отображение отображением на У? в) Пусть X — множество всех кругов, а У — множество всех действительных чисел. Поставим каждому кругу в соответствие длину его радиуса. Мы получим отображение множества X в множество У. Другое отображение X в У получится, если поставить каждому кругу в соответствие его площадь. г) Пусть X — множество всех треугольников, а У — множество всех окружностей. Поставим каждому треугольнику в соответствие вписанную в него окружность. Получим отображение множества X в У. Другое отображение X в У получится, если поставить в соответствие каждому треугольнику описанную вокруг него окружность. д) Пусть У — множество всех деревьев на земном шаре, а X — множество всех плодов, растущих на этих деревьях. Поставим каждому плоду в соответствие дерево, на котором он растет. Получим отображение множества X в множество У.
, связывающее с элементом х множества X элемент множества У, задает отображение X в У. Является ли это отображение отображением на У? в) Пусть X — множество всех кругов, а У — множество всех действительных чисел. Поставим каждому кругу в соответствие длину его радиуса. Мы получим отображение множества X в множество У. Другое отображение X в У получится, если поставить каждому кругу в соответствие его площадь. г) Пусть X — множество всех треугольников, а У — множество всех окружностей. Поставим каждому треугольнику в соответствие вписанную в него окружность. Получим отображение множества X в У. Другое отображение X в У получится, если поставить в соответствие каждому треугольнику описанную вокруг него окружность. д) Пусть У — множество всех деревьев на земном шаре, а X — множество всех плодов, растущих на этих деревьях. Поставим каждому плоду в соответствие дерево, на котором он растет. Получим отображение множества X в множество У.
Пусть 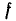 — отображение множества X в множество У и пусть
— отображение множества X в множество У и пусть 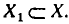 Множество всех элементов вида у
Множество всех элементов вида у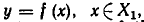 называется образом множества
называется образом множества 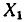 при отображении
при отображении 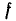 и обозначается
и обозначается 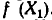
Рассмотрим некоторый элемент у из множества У и возьмем все элементы х из X, отображающиеся в у при отображении 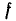 . Множество всех этих элементов называют полным прообразом элемента у при отображении
. Множество всех этих элементов называют полным прообразом элемента у при отображении 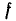 и обозначают
и обозначают 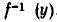 . В первом примере в) полным прообразом положительного числа r является множество всех кругов радиуса r. В первом примере г) полным прообразом любой данной окружности является множество всех треугольников, описанных вокруг этой окружности.
. В первом примере в) полным прообразом положительного числа r является множество всех кругов радиуса r. В первом примере г) полным прообразом любой данной окружности является множество всех треугольников, описанных вокруг этой окружности.
Если полный прообраз каждого элемента у из У при отображении 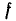 или пуст, или состоит только из одного элемента, то отображение
или пуст, или состоит только из одного элемента, то отображение 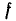 называется вложением в У. Например, функция
называется вложением в У. Например, функция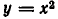 с отрезком [1, 4] в качестве области определения определяет вложение этого отрезка в действительную ось.
с отрезком [1, 4] в качестве области определения определяет вложение этого отрезка в действительную ось.
Если 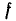 есть отображение множества X на множества У и полный прообраз каждого элемента у из У состоит лишь из одного элемента, то отображение
есть отображение множества X на множества У и полный прообраз каждого элемента у из У состоит лишь из одного элемента, то отображение 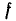 называется взаимно-однозначным отображением множества X на множество У. Иными словами, отображение взаимно-однозначно, если каждый элемент из его области значений является образом одного и только одного элемента его области определения.
называется взаимно-однозначным отображением множества X на множество У. Иными словами, отображение взаимно-однозначно, если каждый элемент из его области значений является образом одного и только одного элемента его области определения.
Краткие исторические сведения
Теоретико-множественные представления в неявной форме давно использовались математиками. Геометры древней Греции в III веке до н. э. рассматривали «геометрические места точек», то есть множества точек, обладающих тем или иным свойством. Однако трудности, связанные с понятием бесконечности, привели к тому, что в течение длительного времени математики избегали рассматривать геометрические фигуры как множества точек.
Исследования по бесконечным множествам начали чешский ученый Б. Больцано (1781— 1841) и немецкий математик Г. Кантор (родился в 1845 г. в Петербурге, умер в 1918 г. в Галле). Труд Больцано был опубликован лишь через много лет после его смерти. Основные заслуги в развитии теории множеств принадлежат Кантору. Он пришел к проблемам этой теории, исходя из сравнительно узкой математической задачи (вопроса о сходимости и расходимости тригонометрических рядов). Однако вскоре ему и его последователям стало ясно, что теория множеств имеет важнейшее значение для различных областей математики. Сейчас теория множеств дает общепринятый язык для многих разделов математики. В целом ряде случаев применение теоретико-множественных понятий позволило привести в систему многие ветви математики. Большой вклад в теорию множеств сделан трудами советских математиков П. С. Александрова, А. Н. Колмогорова, Н. Н. Лузина, П. С. Новикова, М. Я. Суслина и других. Советская школа теории множеств оказала сильное влияние на развитие этой части математики во всем мире.
Вскоре после создания теории множеств выяснилось, что «наивная» трактовка понятия бесконечного множества может привести к противоречиям. Исследования в этом направлении потребовали развития математической логики. Первоначально эта область математики была очень далека от практических приложений, но впоследствии ее принципы составили идейную основу конструирования электронных вычислительных машин и программирования вычислений на этих машинах.
Правила действий над высказываниями, во многом известные еще Аристотелю (создателю формальной логики), были более подробно сформулированы Г. В. Лейбницем, которого часто считают создателем математической логики. Алгебраическую форму этим правилам придали английские математика Дж. Буль (1815— 1864) и А. де Морган (1806—1871). По сути дела, эти правила совпадают с указанными выше правилами действий над множествами. Большой вклад в развитие математической логики внесли Г. Фреге, Б. Рассел, Д. Гильберт, К. Гёдель, А. Тарский, советские математики П. С. Новиков, А. Н. Колмогоров, А. А. Марков и другие.
Дополнение к различным типам множеств











Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат










![{displaystyle bigcup limits _{nin mathbb {Z} }[n,n+1]=mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3835f4db48045c5a8bebe8bf50c998c384adab7c)



