Как найти сумму двух отрицательных чисел

Ноль – это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:

• Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

((-2)+(-3)=-5)

• Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

((-8)+4=4-8=-4)

(9+(-4)=9-4=5)

Для каждого числа кроме (0) существует противоположный элемент, при сумме с ним образуется ноль:

(-9+9=0)     (7,1+(-7,1)=0)

• При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

((-7)-(-6)=(-7)+6=(-1))

• Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

(7-9=-2) так как (9>7)

• Также не стоит забывать минус на минус дает плюс:

(7-(-9)=7+9=16)

1.  (4+(-5))
2.  (-36+15)
3. ((-17)+(-45))
4. (-9+(-1))

Решение:

1.  (4+(-5)=4-5=-1)
2.  (-36+15=-21)
3. ((-17)+(-45)) (=-17-45=-62)
4. (-9+(-1)=-9-1=-10)

1. (3-(-6))
2.  (-16-35)
3. (-27-(-5))
4.  (-94-(-61))

Решение:

1.  (3-(-6)=3+6=9)
2. (-16-35=-51)
3.  (-27-(-5)=-27+5=-22)
4.  (-94-(-61)=-94+61=-33)

Отрицательные числа складываются точно так же как и положительные. При этом знак “минус” сохраняется. Пример. -2+ (-2)= -2-2 (открыли скобки)=-4. К сожалению автор под ником Darli ing ошибся. При сложении и вычитании знак “минус” сохраняется. Знак “минус” переходит в “плюс” только при умножении или делении отрицательных чисел друг на друга. автор вопроса выбрал этот ответ лучшим Степа­н-16 [34.5K] 5 лет назад  Если два числа имеют одинаковый знак: “плюс” или “минус”, то они складываются, а результат будет иметь тот же знак, что и суммируемый числа. То есть, вначале сложили, записали результат, проставили знак. SIRIN­A [41.5K] 8 лет назад  Для сложения двух отрицательных чисел необходимо сложить их модули, то есть число без знака “минус”. В итоге получается сумма двух чисел, но перед суммой нужно поставить знак “минус”. Например:-2 -2=(-2)+(-2)=-(2+2)=-4. Существует даже правило сложения отрицательных чисел −a и −b в виде: (−a)+(−b)=−(a+b). Понять принципы сложения отрицательных чисел сложно потому, что в обыденной жизни мы никогда не сталкиваемся с минус одним яблоком или минус пятеркой за ответ на уроке, то есть отрицательные числа для большинства столь же абстрактны, как и мнимые. Хотя вот бухгалтера любят иметь дело с отрицательными числами и выводить их в плюс. При сложении этих чисел следует помнить, что минус никуда не денется. Проще всего сложить такие числа как обычные положительные числа, а потом просто добавить перед суммой минус, то есть складывать модули чисел: -|2+4|=-6 Точно также следует поступать и при вычитании таких чисел, причем если результат вычитания модулей окажется отрицательным, то добавленный минус сделает его положительным: -|2-4|=-(-2)=2 Ксарф­акс [156K] 5 лет назад  Предположим, у нас имеются два отрицательных числа a и b. a = – 5. b = – 10. Сумма отрицательных чисел = a + b = -5 + (-10) = -5 – 10 = -(5+10) = -15. Таким образом, становится понятно, что для сложения нескольких отрицательных чисел нужно сложить их модули, а затем к результату приписать знак минус: -a + (-b) = -(|a|+|b|). Просто достаточно помнить, что при суммировании двух отрицательных чисел мы всегда получаем ещё большее уменьшение (сумма будет находится на числовой оси левее обоих слагаемых). Skiye­rs [121K] 8 лет назад  На миг забудьте о том, что перед цифрами стоят минусы и сплюсуйте их. А потом вспоминайте и к результату добавьте минус. Например, если сложить -5 и -3, то получится -8. А вот если к отрицательному числу надо добавить положительное (пример -2+4), то просто поменяйте их местами (+4-2), и вы поймете, что ответом будет 2. Galin­a7v7 [120K] 6 лет назад  Для сложения двух ( и более) отрицательных чисел нужно, не обращая внимания на знаки минус сложить модули (значения без знака минус), и к результату ” приписать знак минус.Для примера : -115 – 97 = -( 115 + 97) = – 212. -3 -4 -5 =-(3+4+5) = -12 И более простой пример: -1 -3 =-(1 +3)=-4 Olbas­t [11.5K] 8 лет назад  Сложение отрицательных чисел происходит точно также как и положительных. Складываете цифры, а перед полученным результатом ставите знак “-“. Пример: -4 + (-6)= -10. Это правило действует только для сложения. В случае умножения: “-” * “-” = +; В случае деления: “-“/”-“= +. Алиса в Стран­е [363K] 5 лет назад  Если оба ваши числа отрицательные, то при сложении можно просто забыть о минусах, стоящих перед ними, сложите эти числа так, как будто бы они были положительными, но потом перед суммой поставьте знак минус. -132 + (-68), это все равно что -(132 + 68) = -200 Azama­tik [55.3K] 5 лет назад  Если нужно сложить два числа с отрицательным знаком, знак [–] выносится за скобки, а числа складываются. Отрицательный знак сохраняется. Итак, примеры: Нужно сложить -32 и -48. -32 + (-48) = – (32 + 48) = – 80. Второй пример: -10 + (-60) = – (10+60) = – 70. Знаете ответ?

План урока:

Сложение отрицательных чисел

Сложение чисел с разными знаками

Вычитание отрицательных чисел и чисел с разными знаками

Сложение  и вычитание отрицательных чисел

Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.

В театре Карабаса-Барабаса актерам жилось очень сложно, все куклы мечтали  жить на свободе. Актеры тяжело работали,  но долги перед хозяином росли с каждым днем. Злой владелец пообещал отпустить Буратино и Мальвину из своего театра только тогда, когда кукольные герои вернут ему долг. Сколько монет нужно собрать героям, чтобы оказаться на свободе, если у Буратино было -15 монет, а у Мальвины -6?

Чтобы ответить на главный вопрос задачи, нам нужно понимать, о чем идет речь. Изучив условие, возникает вопрос «Как может быть -15 и -6 монет?». В данном случае выходит, что Буратино и Мальвина должны вернуть Карабасу-Барабасу 15 и 6 монет, поэтому перед данными числами и стоит знак «минус». Получается, кукольные персонажи смогут покинуть театр, когда полностью вернут долг. Для этого необходимо узнать общий размер долга Буратино и Мальвины. Чтобы узнать размер долга, суммируем монеты персонажей -15 и -6. Но как их сложить, когда перед слагаемыми стоит «минус»? В подобных ситуациях применяют правило сложения отрицательных чисел.

Возвращаемся к решению задачи.

Теперь, правильно запишем и суммируем известные данные.

Получается, что герои имеют -21 монету, следовательно, они должны собрать 21 монету и вернуть долг, только тогда появится возможность покинуть театр Карабаса-Барабаса.

Источник

Рассмотрим еще одно задание.

Найдите результат сложения -24 и -16.

Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».

-24+(-16)=-(24+16)=-40.

Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».

Сложение чисел с разными знаками

Рассмотрим ситуацию.

Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?

Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.

Суммируем-3 и 10. Для этого:

• определяем модули: -3=|3|, 10=|10|;
• сравниваем модули, определяя больший: |3|<|10|;
• от большего отнимаем меньший: 10 – 3=7;
• так как по условию 10 – число положительное, то и результат будет числом положительным.

Записывается в таком виде:

-3+10=10 – 3=7.

Выходит, у мальчика стало 7 яблок.

Рассмотрим еще один пример сложения чисел с разными знаками.

Вычислите сумму -28 и 11.

Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.

-28=|28|;

11=|11|;

28>11.

Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:

-28+11=-(28-11)=-17.

Учитывая рассмотренные примеры, можно сказать, что:

любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.

Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.

Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:

-150+50=-(150-50)=-100.

Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:

При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.

-150=|150|;

-100=|100|.

150>100;

-150<-100.

Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.

Вычитание отрицательных чисел и чисел с разными знаками

Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:

Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.

Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.

Определите, чему будет равно значение выражения: от -510 отнять +210.

На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:

-510-(+210)

Сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:

Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.

Например: -5-(+2).

Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).

По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:

-5+(-2)=-(5+2)=-7

Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:

Запишем выражение:

-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:

-510-(+210)=-510+(-210)=-(510+210)=-720.

Вычисления окончены.

Источник

Рассмотрим следующее задание.

Найдите значение выражения: -248+248.

Используем правило сложения значений с разными знаками.

-248=|248|;

248=|248|;

248 – 248=0.

Следовательно, при сложении противоположных числовых значений в результате всегда будет 0.

Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.

К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.

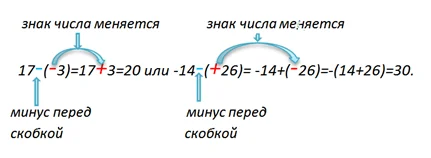
Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».

Вычисли: -36+(-7).

В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.

В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.

Минутка истории

История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.

Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом   .

Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.

Сегодня на уроке мы продолжим изучение темы сложение
чисел. Научимся складывать отрицательные числа и выведем алгоритм сложения
отрицательных чисел.

Давайте посмотрим, что происходит при сложении чисел
– 2 и – 5.
Для наглядности будем складывать числа с помощью координатной прямой.

Отметим точку А
с координатой – 2. Число – 5 отрицательное. Следовательно, мы
должны точку А переместить влево
на 5 единичных отрезков.

Видно, что точка А
переместится в точку В с координатой – 7.

Значит, (-2) + (-5) = -7.

Как получилось здесь число 7?

Это сумма 2 + 5,
т.е. сумма модулей слагаемых – 2 и – 5.

Смотрите, что мы получаем (-2)
+ (-5) = – (2 + 5) = -7.

Сделаем вывод:

Чтобы сложить два отрицательных числа,
нужно взять сумму их модулей со знаком «минус».

Задание

Найти сумму чисел:

1)   
– 1 и – 7;
2) – 2,5 и – 4,5;
3)  и
;
4)  и
.

Решение:

Теперь мы можем записать алгоритм сложения
отрицательных чисел.

Для того чтобы сложить два отрицательных числа,
нужно:

1)    сложить
модули этих чисел,

2)    перед
полученным числом поставить знак «минус».

Задание

Найдите значение выражения:

– 27 + (- 9) + (- 13) + (- 41)

Решение:

Итоги

Для того чтобы сложить два отрицательных числа,
нужно:

1)    сложить
модули этих чисел,

2)    перед
полученным числом поставить знак «минус».