Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 марта 2023 года; проверки требуют 6 правок.
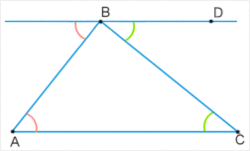
Теорема о сумме углов треугольника — классическая теорема евклидовой геометрии.
Формулировка[править | править код]
Сумма углов любого треугольника на евклидовой плоскости равна 180°.[1]
Доказательство[править | править код]
Пусть 
Следствия[править | править код]
- В треугольнике не может быть двух тупых или двух прямых углов, потому что тогда сумма углов была бы больше 180°. По той же причине треугольник не может содержать тупой и прямой углы одновременно.
- У любого треугольника не меньше двух острых углов. Действительно, случай, когда у треугольника только один острый угол или вообще нет острых углов, противоречит предыдущему следствию.
- В прямоугольном треугольнике оба угла при гипотенузе — острые.
- В равнобедренном треугольнике углы при основании равны, поэтому тупым может быть только угол, противолежащий основанию.
- В равнобедренном прямоугольном треугольнике углы при гипотенузе равны (180° — 90°) /2 = 45°.
- В равностороннем треугольнике все три угла совпадают и поэтому равны 180° / 3 = 60°.
- (Теорема о внешнем угле треугольника) Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним[2].
Вариации и обобщения[править | править код]
Многоугольники[править | править код]
Обобщение для симплексов[править | править код]
Существует более сложное соотношение между двугранными углами произвольного симплекса. А именно, если 
.
Это следует из того, что этот определитель является определителем Грама нормалей к граням симплекса, а определитель Грама линейно зависимых векторов равен 0, и 

В неевклидовых геометриях[править | править код]

Приведённое в этой статье доказательство опирается на определённое свойство параллельных прямых, а именно — утверждение о том, что внутренние накрест лежащие углы при параллельных прямых равны. Доказательство этого утверждения, в свою очередь, использует аксиому параллельности евклидовой геометрии. Можно показать, что любое доказательство теоремы о сумме углов треугольника будет использовать аксиому параллельности, и наоборот — из утверждения, что сумма углов треугольника равна 180°, можно вывести аксиому параллельности, если даны остальные аксиомы классической геометрии (абсолютная геометрия)[3].
Таким образом, равенство суммы углов треугольника 180° является одним из основных признаков именно евклидовой геометрии, отличающих её от неевклидовых, в которых аксиома параллельности не выполняется:
- На сфере сумма углов треугольника всегда превышает 180°, разница называется сферическим избытком и пропорциональна площади треугольника. У сферического треугольника могут быть два или даже три прямых или тупых угла.
-
- Пример. Одна вершина треугольника на сфере — северный полюс. Этот угол может иметь значение до 180°. Две другие вершины лежат на экваторе, соответствующие углы равны 90°.
- В геометрии Лобачевского сумма углов треугольника всегда меньше 180° и может быть сколь угодно малой. Разность также пропорциональна площади треугольника.
Примечания[править | править код]
- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 81.
- ↑ Элементарная математика, 1976, с. 421.
- ↑ Лелон-Ферран Ж. Основания геометрии. — М.: Мир, 1989. — С. 255—256. — 312 с. — ISBN 5-03-001008-4.
Литература[править | править код]
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Сумма углов треугольника равна (180°).

Доказательство
Рассмотрим произвольный треугольник (KLM) и докажем, что
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
1. Через вершину (L) параллельно стороне (KM) проведём прямую (a).
2. При пересечении параллельных прямых (a) и (KM) секущей (KL), углы, которые обозначаются (1), будут накрест лежащими углами, а углы, обозначенные (2) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е.
∠
(1) (+)
∠
(2) (+)
∠
(3 =)
180°
, или
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна
90°
.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен
45°
.
Следствие 3. В равностороннем треугольнике каждый угол равен
60°
.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Доказательство
Из равенств
∠
(KML) (+)
∠
(BML=)
180°
и
∠
(K) (+)
∠
(L) (+)
∠
(KML =)
180°
получаем, что
∠
(BML =)
∠
(K) (+)
∠
(L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.

У треугольника (KLM) все углы острые.

У треугольника (KMN) угол (K = 90)
°
.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.

У треугольника (KLM) один угол тупой.
Сумма углов треугольника:
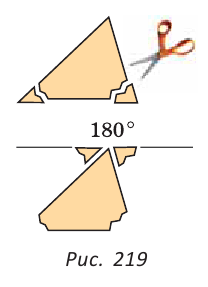
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.

Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
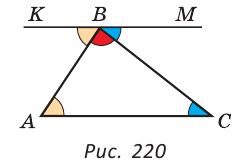
Теорема. Сумма углов треугольника равна 180°.
Дано:  АВС (рис. 220).
АВС (рис. 220).
Доказать:  A+
A+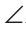 B +
B +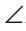 C = 180°.
C = 180°.
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 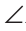 KBA =
KBA =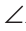 A как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей АВ, a
A как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей АВ, a MBC =
MBC = C как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей ВС. Так как углы КВА, ABC и МВС образуют развернутый угол, то
C как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей ВС. Так как углы КВА, ABC и МВС образуют развернутый угол, то
 KBA +
KBA + ABC +
ABC + MBC = 180°. Отсюда
MBC = 180°. Отсюда A +
A + B +
B + C = 180°. Теорема доказана.
C = 180°. Теорема доказана.
Следствия.
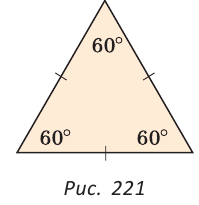
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
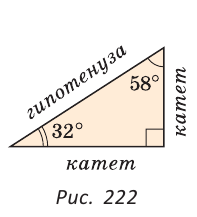
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то 1 =
1 =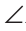 2.
2.
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
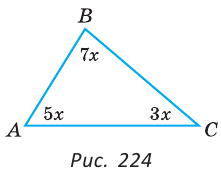
Решение:
Пусть 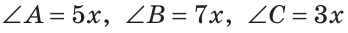 (
(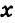 — градусная мера одной части).
— градусная мера одной части).
Так как сумма углов треугольника равна 180°, то
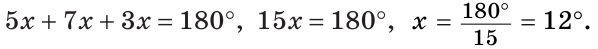
Тогда 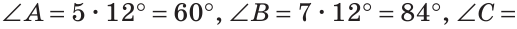
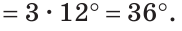
Ответ: 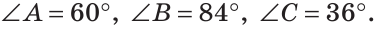
Пример:
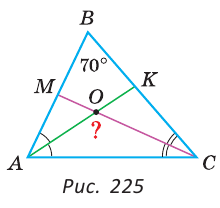
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° – 70° = 110°. Так как биссектриса делит угол пополам, то
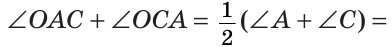
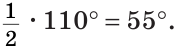
Из треугольника АОС находим: 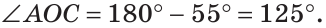
Ответ: 125°.
Замечание. Если 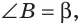 то, рассуждая аналогично, получим формулу:
то, рассуждая аналогично, получим формулу: 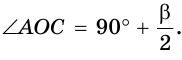 Если, например,
Если, например, 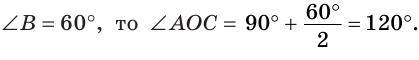
Пример:
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
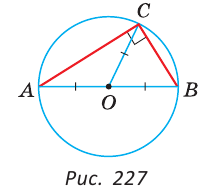
Пусть СМ — медиана, 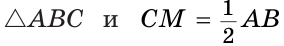 (рис. 226).
(рис. 226).
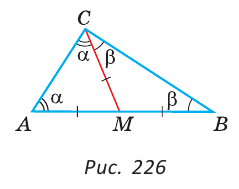
Докажем, что ACB = 90°. Обозначим
ACB = 90°. Обозначим  A =
A =  ,
, В =
В =  . Так как медиана делит сторону пополам, то AM = MB =
. Так как медиана делит сторону пополам, то AM = MB =  АВ. Тогда СМ=АМ=МВ. Так как
АВ. Тогда СМ=АМ=МВ. Так как  АМС — равнобедренный, то
АМС — равнобедренный, то A =
A = ACM =
ACM =  как углы при основании равнобедренного треугольника. Аналогично,
как углы при основании равнобедренного треугольника. Аналогично,  СМВ — равнобедренный и
СМВ — равнобедренный и  B =
B = BCM =
BCM =  . Сумма углов треугольника ABC, с одной стороны, равна 2
. Сумма углов треугольника ABC, с одной стороны, равна 2 + 2
+ 2 , с другой — равна 180°. Отсюда 2
, с другой — равна 180°. Отсюда 2 + 2
+ 2 = 180°, 2(
= 180°, 2( +
+  ) = 180°,
) = 180°,  +
+  = 90°. Но
= 90°. Но ACB =
ACB =  +
+  , поэтому
, поэтому
 ACB = 90°.
ACB = 90°.
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228)  C=90°,
C=90°, A=
A= ,
, B=
B= .
.
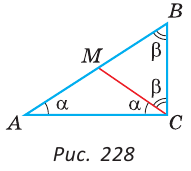
Проведем отрезок СМ так, что ACM=
ACM= , и докажем, что СМ — медиана и что СМ=
, и докажем, что СМ — медиана и что СМ= АВ. Угол В дополняет угол А до 90°, a
АВ. Угол В дополняет угол А до 90°, a BCM дополняет
BCM дополняет ACM до 90°. Поскольку
ACM до 90°. Поскольку  ACM =
ACM = A =
A =  , то
, то BCM =
BCM = . Треугольники АМС и ВМС — равнобедренные по признаку равнобедренного треугольника. Тогда AM = МС и МВ = МС. Отсюда СМ — медиана и СМ =
. Треугольники АМС и ВМС — равнобедренные по признаку равнобедренного треугольника. Тогда AM = МС и МВ = МС. Отсюда СМ — медиана и СМ =  АВ.
АВ.
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Теорема о сумме углов треугольника
Теорема
Данная теорема является одной из важнейших теорем геометрии.
Доказательство
Дано:  ABC
ABC
Доказать:  A+
A+ B+
B+ C=1800
C=1800
Доказательство:
Нам дан  ABC
ABC
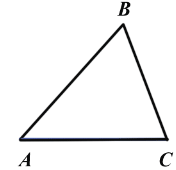
Проведем прямую a AC, проходящую через вершину B и обозначим углы.
AC, проходящую через вершину B и обозначим углы.
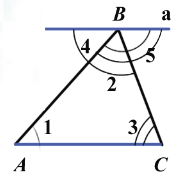
Углы 1 и 4; 3 и 5 будут являться накрест лежащими углами при параллельных прямых a и AC, секущих AB и BC соответственно, 
 4 =
4 = 1,
1,  5 =
5 = 3.
3.
Из построения мы видим, что сумма углов 4, 2 и 5 равна развёрнутому углу с вершиной B, значит  4+
4+ 2+
2+ 5 = 1800.
5 = 1800.  , учитывая то, что
, учитывая то, что  4 =
4 = 1,
1,  5 =
5 = 3, можем записать, что
3, можем записать, что  1+
1+ 2+
2+ 3 = 1800, или
3 = 1800, или  A+
A+ B+
B+ C = 1800. Что и требовалось доказать.
C = 1800. Что и требовалось доказать.
Внешний угол треугольника – это угол, смежный с каким-нибудь углом этого треугольника.
Доказательство:
Пусть нам дан треугольник, в котором  3 и
3 и  4 смежные (т.е.
4 смежные (т.е.  4 является внешним углом данного треугольника)
4 является внешним углом данного треугольника)
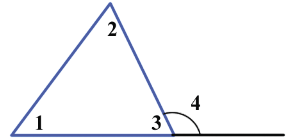
Так как данные углы смежные мы можем записать, что  3 +
3 + 4 = 1800, а по теореме о сумме углов треугольника (
4 = 1800, а по теореме о сумме углов треугольника ( 1 +
1 + 2) +
2) +  3 = 1800. Из данных выражений мы видим, что
3 = 1800. Из данных выражений мы видим, что  4 =
4 =  1 +
1 + 2. Что и требовалось доказать.
2. Что и требовалось доказать.
Советуем посмотреть:
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 242,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 335,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 377,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 541,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 678,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 703,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 854,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1038,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1146,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 433,
Мерзляк, Полонский, Якир, Учебник
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 7 класс. Задачи на применение теоремы о сумме углов треугольника. Они встречаются в 15 задании ОГЭ по математике.
Вспомним теорему о сумме углов треугольника:
Сумма углов в треугольнике равна 180 градусам.
Задача №1
Решение
Сумма всех углов в треугольнике равна 180 градусам. Нам известны два угла в треугольнике. Они равны 72 и 42 градуса. Значит, третий угол равен:
Ответ 66
Задача №2
Решение
Отметив известный угол на чертеже. Необходимо найти внешний угол треугольника, который обозначен красным цветом.
Внешний угол треугольника – называется угол, который смежный с каким-нибудь внутренним углом этого треугольника.
Свойство смежных углов:
Смежный угол треугольника равен 180 градусам.
Рядом с чертежом треугольника сделаем смежные углы.
Теперь найдем угол, смежный с углом в 115 градусов.
Ответ 65
Задача №3
Решение
В треугольнике АВС АВ=ВС, т.е. две стороны равны. Значит треугольник равнобедренный. Третья сторона – основание.
Свойство равнобедренного треугольника:
В равнобедренном треугольнике углы при основании равны
Отметим на чертеже равные углы одинаковыми дугами и известный угол АВС.
Ответ 37
Задача №4
Решение
Прямой угол на чертеже обозначается квадратиком и равен 90 градусов.
Отметим на чертеже все известные углы
Решение задачи через теорему о сумме углов в треугольнике:
Решение задачи через свойство прямоугольного треугольника
Сумма острых углов прямоугольного треугольника равна 90 градусам
Ответ 69
Задача №5
Решение
Отметим на чертеже известные углы. Для того чтобы найти угол АВН, нужно рассмотреть треугольник АВН (прямоугольный с прямым углом АНВ=90). В решении этой задачи можно воспользоваться теоремой о сумме углов треугольника или свойством острых углов прямоугольного треугольника.
Ответ 53
Задача №6
Решение
Отметим на рисунке равные стороны, известные углы и то, что нужно найти.
Так как в треугольнике АВС стороны АС и ВС равны, то треугольник АВС равнобедренный. В равнобедренном треугольнике углы при основании равны (отмечено синими дугами).
Найдем внутренний угол треугольника при внешнем угле в 125 градусов
Вычислим угол АСВ применив теорему о сумме углов в треугольнике
Задача №7
Решение
Для решения этой задачи, нам необходимо вспомнить, что такое биссектриса и ее свойстве. Об этом было сказано здесь
Коротко: Биссектриса делит угол на две равные части. Отметим на рисунке, какие углы у нас получатся. Разделим углы М и N пополам и отметим это на чертеже.
Найдем градусную меру угла NAM по теореме о сумме углов в треугольнике
Ответ 117.
Задание №8
Решение
Отметим на чертеже известные углы и то, что надо найти.
Для решения необходимо найти еще угол ALB, смежный с углом ALC.
Теперь можно вычислить угол BAL который равен углу LAC по свойству биссектрисы угла треугольника.
Воспользуемся теоремой о сумме углов в треугольнике и вычислим угол ACB
Ответ 16.
Задача №9
Решение
Из первого предложения задачи выясняем, что треугольник ADC – равнобедренный, так как AD=AC. Отметим это на чертеже и вычислим углы при основании треугольника ADC.
Нам необходимо найти градусную меру угла DCB.
Ответ 53,5
Задача №10
Решение
Так как углы А и С известны, то можем найти угол В по теореме о сумме углов в треугольнике.
Так как BD биссектриса в треугольнике ABC, то углы ABD и CBD равны.
Рассмотрим прямоугольный треугольник CHB. В треугольнике CHB по свойству острых углов в прямоугольном треугольнике найдем острый угол СВН.
Осталось по задаче найти градусную меру угла DBH.
Ответ 20
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
