Сумма нескольких векторов
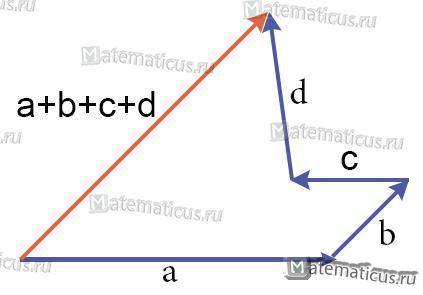
Сумма нескольких векторов а 1, а 2, а 3, … , а n, это вектор, получающийся после ряда последовательных сложений: к вектору а 1 прибавляется вектор а 2, к полученному вектору прибавляется вектор а 3 и т.д.
Из определения вытекает такое построение
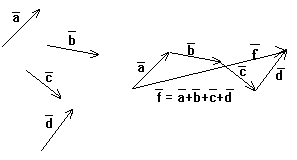
Правило многоугольника или правило цепи
Из произвольного начала О строим вектор ОА 1 = а 1, из точки А 1, как из начала, строим вектор А 1 А 2 = а 2, из точки А 2 строим вектор А 2 А 3 = а 3 и т.д. Вектор ОА n (на рисунке n = 6) есть сумма векторов а 1, а 2, … , а n.
Свойство сочетательности
Слагаемые векторы можно группировать как угодно.
Так, если найти сначала сумму векторов
и к ней прибавить вектор а 1 ( ОА 1), то получим то же вектор:
Правило параллелепипеда
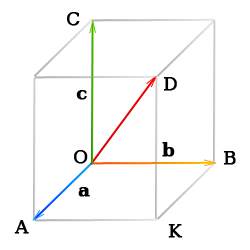
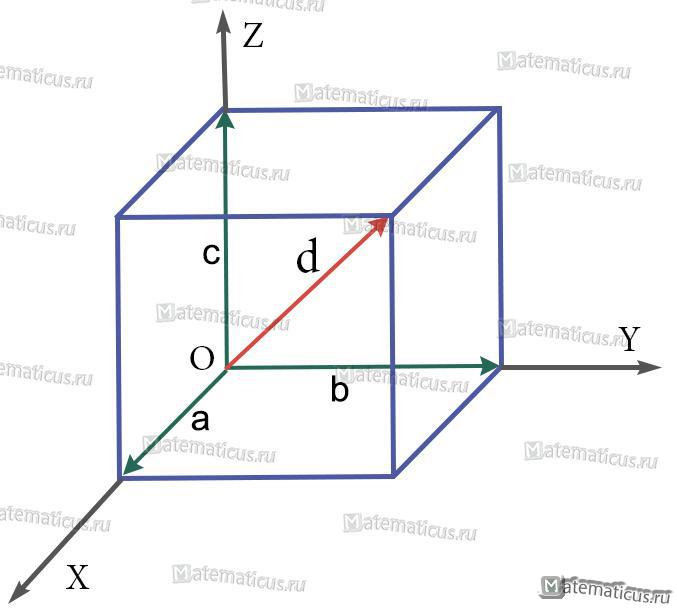
Если три вектора а , b , с после приведения к общему началу не лежат в одной плоскости, то сумму а + b + c можно найти таким построением:
Из любого начала О строим векторы ОА = а , ОВ = b , ОС = с , на отрезках ОА , ОВ , ОС , как на ребрах, строим параллелепипед. Вектор диагонали OD есть сумма векторов a , b , и c (так как ОА = а , АК = ОВ = b , KD = OC = c и OD = OA + AK + KD ).
К векторам, которые (после приведения к общему началу) лежат в одной плоскости, это построение неприменимо.
Правило параллелепипеда. Разложение вектора
Вы будете перенаправлены на Автор24
Правило параллелепипеда
Для правила сложения трех векторов рассмотрим следующую задачу.
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $overrightarrow
$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
Доказательство.
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:
[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow
=overrightarrow]
Рассмотрим следующий рисунок:
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Тогда, получаем, что
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow
$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:
Вычтем эти разложения друг из друга
Из этого получаем
Теорема доказана.
Онлайн калькулятор. Сложение и вычитание двух векторов.
Этот онлайн калькулятор позволит вам очень просто найти сумму двух векторов или разность двух векторов для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на сложение и вычитание двух векторов и закрепить пройденый материал.
Калькулятор для сложения и вычитания двух векторов
Введите значения векторов.
Инструкция использования калькулятора для сложения и вычитания двух векторов
Ввод даных в калькулятор для сложения и вычитания двух векторов
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для сложения и вычитания двух векторов
- Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.
Теория. Сложение и вычитание двух векторов
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://spravochnick.ru/matematika/dekartovy_koordinaty_i_vektory_v_prostranstve/pravilo_parallelepipeda_razlozhenie_vektora/
http://ru.onlinemschool.com/math/assistance/vector/calc/
[/spoiler]
Сумма нескольких векторов
Сумма нескольких векторов а1, а2, а3, … , аn, это вектор, получающийся после ряда последовательных сложений:
к вектору а1 прибавляется вектор а2, к полученному вектору прибавляется вектор а3 и т.д.
Из определения вытекает такое построение
Сумма нескольких векторов
Правило многоугольника или правило цепи
Из произвольного начала О строим вектор ОА1 = а1,
из точки А1, как из начала, строим вектор А1А2 = а2,
из точки А2 строим вектор А2А3 = а3 и т.д.
Вектор ОАn (на рисунке n = 6) есть сумма векторов а1, а2, … , аn.
Сумма векторов а1, а2, а3, а4, а5, а6 обозначается
[ vector{a_1}+vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6} ]
Свойство сочетательности
Слагаемые векторы можно группировать как угодно.
Так, если найти сначала сумму векторов
[ vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6} = vector{A_1 A_6} ]
и к ней прибавить вектор а1 (ОА1), то получим то же вектор:
[ vector{a_1}+(vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6}) = \ = vector{a_1}+vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6} ]
Правило параллелепипеда
Если три вектора а, b, с после приведения к общему началу не лежат в одной плоскости, то сумму а+b+c можно найти таким построением:
Правило параллелепипеда — Сумма нескольких векторов
Из любого начала О строим векторы ОА = а, ОВ = b, ОС = с,
на отрезках ОА, ОВ, ОС, как на ребрах, строим параллелепипед.
Вектор диагонали OD есть сумма векторов a, b, и c
(так как ОА = а, АК = ОВ = b, KD = OC = c и OD = OA + AK + KD).
Сумма нескольких векторов |
стр. 172 |
|---|
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Правило параллелепипеда
Для правила сложения трех векторов рассмотрим следующую задачу.
Пример 1
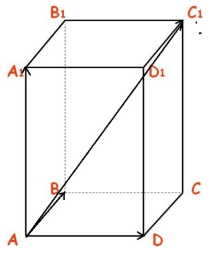
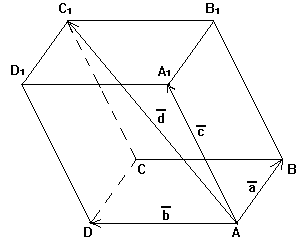
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow{AB}+overrightarrow{AD}+overrightarrow{AA_1}=overrightarrow{AC_1}$
Рисунок 1.
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:
[overrightarrow{AC_1}=overrightarrow{AC}+overrightarrow{CC_1}=overrightarrow{AD}+overrightarrow{DC}+overrightarrow{CC_1}]
Так как $overrightarrow{DC}=overrightarrow{AB}, overrightarrow{CC_1}=overrightarrow{AA_1}$
То есть
[overrightarrow{AC_1}=overrightarrow{AB}+overrightarrow{AD}+overrightarrow{AA_1}]
ч. т. д.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow{a},overrightarrow{b} и overrightarrow{c}$ нужно от произвольной точки $O$ отложить векторы $overrightarrow{AB}=overrightarrow{a}$, $overrightarrow{AC}=overrightarrow{b}$ и $overrightarrow{AA_1}=overrightarrow{c}$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow{AC_1}$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Определение 1
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $overrightarrow{p}$ можно разложить по трем некомпланарным векторам $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
[overrightarrow{p}={alpha }_1overrightarrow{a_1}+{alpha }_2overrightarrow{a_2}+{alpha }_3overrightarrow{a_3}]
Доказательство.
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$. Выберем произвольную точку $O$ и построим следующие векторы:
[overrightarrow{a_1}=overrightarrow{OA}, overrightarrow{a_2}=overrightarrow{OB}, overrightarrow{a_3}=overrightarrow{OC} и overrightarrow{p}=overrightarrow{OP}]
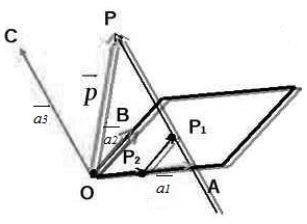
Рассмотрим следующий рисунок:
Рисунок 2.
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow{OC}$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow{OB}$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:
[overrightarrow{OP}=overrightarrow{p}=overrightarrow{OP_2}+overrightarrow{P_2P_1}+overrightarrow{P_1P}]
Так как векторы $overrightarrow{OP_2}$ и $overrightarrow{OA}$ коллинеарны, то
[overrightarrow{OP_2}={alpha }_1overrightarrow{OA}={alpha }_1overrightarrow{a_1}]
Так как векторы $overrightarrow{P_2P_1}$ и $overrightarrow{OB}$ коллинеарны, то
[overrightarrow{P_2P_1}={alpha }_2overrightarrow{OB}={alpha }_2overrightarrow{a_2}]
Так как векторы $overrightarrow{P_1P}$ и $overrightarrow{OC}$ коллинеарны, то
[overrightarrow{P_1P}={alpha }_3overrightarrow{OC}={alpha }_3overrightarrow{a_3}]
Тогда, получаем, что
[overrightarrow{p}=overrightarrow{OP_2}+overrightarrow{P_2P_1}+overrightarrow{P_1P}={alpha }_1overrightarrow{a_1}+{alpha }_2overrightarrow{a_2}+{alpha }_3overrightarrow{a_3}]
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow{p}$ по векторам $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$:
[overrightarrow{p}={alpha ‘}_1overrightarrow{a_1}+{alpha ‘}_2overrightarrow{a_2}+{alpha ‘}_3overrightarrow{a_3}]
Вычтем эти разложения друг из друга
[overrightarrow{p}-overrightarrow{p}={alpha }_1overrightarrow{a_1}+{alpha }_2overrightarrow{a_2}+{alpha }_3overrightarrow{a_3}-{alpha ‘}_1overrightarrow{a_1}-{alpha ‘}_2overrightarrow{a_2}-{alpha ‘}_3overrightarrow{a_3}] [overrightarrow{0}=left({alpha }_1-{{alpha }’}_1right)overrightarrow{a_1}+left({alpha }_2-{{alpha }’}_2right)overrightarrow{a_2}+({alpha }_3-{{alpha }’}_3)overrightarrow{a_3}]
Из этого получаем
[left{ begin{array}{c} {{alpha }_1-{{alpha }’}_1=0,} \ {{alpha }_2-{{alpha }’}_2=0} \ {{alpha }_3-{{alpha }’}_3=0.} end{array} right.]
Следовательно
[left{ begin{array}{c} {{alpha }_1={{alpha }’}_1,} \ {{alpha }_2={{alpha }’}_2,} \ {{alpha }_3={{alpha }’}_3.} end{array} right.]
Теорема доказана.
«Правило параллелепипеда. Разложение вектора» 👇
Пример задачи
Пример 2
Пусть нам дана пирамида $OABCD$. Разложите вектор $overrightarrow{OD}$ по векторам $overrightarrow{OA}, overrightarrow{OB} и overrightarrow{OC}$.
Решение.
Так как векторы $overrightarrow{OA}, overrightarrow{OB} и overrightarrow{OC}$ – стороны пирамиды, то они являются некомпланарными векторами. Тогда, по теореме 1, вектор $overrightarrow{OD}$ можно разложить по этим векторам, причем разложение будет единственно. Для разложения будем пользоваться свойством сложения векторов и равенством векторов.
Видим, что
[overrightarrow{OD}=overrightarrow{OA}+overrightarrow{AD}] [overrightarrow{AD}=overrightarrow{BC}=overrightarrow{BO}+overrightarrow{OC}=overrightarrow{OC}-overrightarrow{OB}]
Следовательно
[overrightarrow{OD}=overrightarrow{OA}+overrightarrow{OC}-overrightarrow{OB}]
Ответ: $overrightarrow{OA}+overrightarrow{OC}-overrightarrow{OB}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
1.
Правилом
треугольника
Суммой двух векторов
и
называется третий вектор
,
соединяющий начало векторас концом вектора
,
при условии, что начало векторапомещено в конец вектора
.
2
Правило
параллелограмм.
Если векторы
и
привести к общему началу и построить
на векторахи
параллелограмм, то диагональ
параллелограмма, выходящая из общего
начала, называется суммой векторови
.
3
Правило
многоугольника. Если
векторы расположить так, чтобы начало
каждого следующего вектора поместить
в конец предыдущего, то суммой нескольких
векторов называется вектор, соединяющий
начало самого первого вектора с концом
последнего
Число слагаемых
векторов может быть любое конечное,
многоугольник в результате сложения
может быть выпуклым, а может и нет .
4.Правило
параллелепипеда. Сумма
трех некомпланарных векторов, приведенных
к общему началу, равна диагонали
параллелепипеда, построенного на этих
векторах, выходящая из общего начала.
.
Если
обозначить
,
тогда получим:
Вычитание
Правило
5 Разностью
двух векторов
и
называется третий вектор
,который
в сумме с векторомдаёт вектор
.
т.е.
.
Если
привести векторы к общему началу и
построить на них параллелограмм, то
диагональ параллелограмма, не выходящая
из общего начала, является разностью
векторов, т.е. разность векторов –
вектор, проведённый из конца вычитаемого
в конец уменьшаемого.
Свойства
(суммы и разности векторов)
Относительно
сложения имеют место законы:
1)
– коммутативный
(переместительный);
2)
– ассоциативный
(сочетательный);
3)
для любого вектора
существует нулевой вектор
,
такой,
что;
4)
для каждого вектора существует вектор
такой, что
вектор
называется противоположным вектору
и обозначается
,
т.е.=-
.
Умножение вектора на число
Правило
6.Произведением
вектора
на число
называется вектор
,
коллинеарный вектору,
длина которого равна,
а направление совпадает с вектором,
если,
и противоположное, если.
.
Относительно
умножения на число имеют место законы:
а)
–распределительный;
б)
–сочетательный
;
в)
–коммутативный.
3. Проекция вектора на ось
Пусть
в пространстве задана ось l.
Опр.10
Проекцией точки М на ось l
называется
основание М1
перпендикуляра
ММ1,
опущенного из точки на ось.
Опр.11.Проекцией
вектора
на ось l
называется длина отрезка,
взятая со знаком «+», если направление
его совпадает с направлением оси и со
знаком «-», если направлениепротивоположно направлению оси.
Обозначается
.
Проекция
вектора на ось равна произведению его
модуля на косинус угла
,
который вектор образует с осью.
При
этом углом
между вектором и осью называется угол,
на который нужно повернуть ось до
совмещения с вектором против хода
часовой стрелки.
4.Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Проекции
вектора на оси координат называются
его координатами. В этом заключается
их геометрический смысл.
Если
задана система координат на плоскости
и в пространстве, то начало вектора
можно всегда совместить с началом
координат, не меняя при этом длину и
направление. Выделим на координатных
осях единичные векторы и обозначим
.Выберем
произвольный вектор.
Найдем проекции вектора на координатные
оси.
Проведем
через конец вектора плоскости, параллельные
координатным плоскостям. Точки пересечения
с осями обозначим соответственно через
М1,М2,М3.
Получили прямоугольный параллелепипед,
одной диагональю которого является
.
Тогда
;
;
.
По определению суммы получим, что
,
но т.к.,то
.
Но
,
,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Skip to content
Сложение векторов
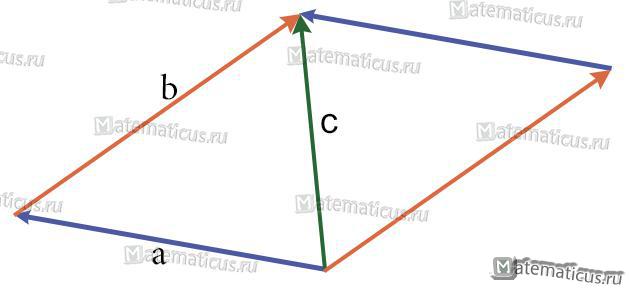
Сложение векторов по правилу параллелограмма
Правило параллелограмма
Если слагаемые a и b не коллинеарны, то
c=a+b
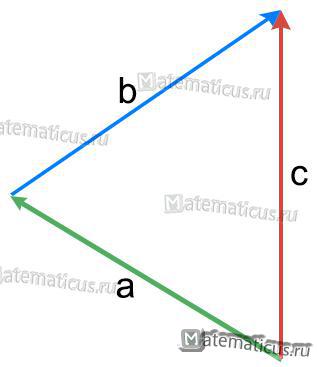
Сложение векторов по правилу треугольника
Правило треугольника
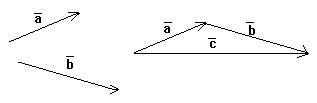
Суммой векторов a (на рисунке зелёный вектор) и b (на рисунке синий вектор) называется третий вектор c (на рисунке красный вектор) , получаемый следующее построение:
Примечание
Нельзя смешивать понятие «сумма отрезков» с понятием «сумма векторов».
Правило параллелепипеда
Если три вектора a, b, c после приведения к общему началу не лежат в одной плоскости , то их сумма равна диагонали параллелепипеда
d=a+b+c
Правило параллелепипеда применяется для сложения трех некомпланарных векторов.
Сложение противоположных векторов
Сумма противоположных векторов равна нуль-вектору, т.е.
a+(-a)=0
Свойство переместительности (переместительный закон)
От перестановки слагаемых сумма векторов не меняется.
с=a+b= b+a
Сочетательное свойство (сочетательный закон)
Слагаемые векторы можно группировать как угодно.
a+(b+c+d) = a+b+c+d
Вычитание векторов
Вычесть вектор а (вычитаемое) из вектора b (уменьшаемое) значит найти новый вектор x (разность), который в сумме с вектором а даёт вектор b.
Разность векторов обозначается: a-b
Вычитание есть действие обратное сложению (сложение векторов).
Вычитание векторов показаны на рисунках ниже:
Примечание
Модуль разности может быть меньше модуля «уменьшаемого», но может быть и больше или равен ему. Эти случаи показаны на рисунке выше.
5620