Для расчета электрической цепи применяют два закона Кирхгофа. (Скорее их можно отнести не к законам, а к правилам. Но в большинстве учебников пишут именно о “законах” Кирхгофа. Поэтому и здесь будем обращаться к законам).
Первый закон Кирхгофа
Первый закон Кирхгофа применяют к узлам электрической цепи и выражают баланс токов в них. Первый закон Кирхгофа гласит:
Алгебраическая сумма токов сходящихся в узле электрической цепи равна 0.
Под словом “алгебраическая” имеется в виду, что учитывается знак перед током: “плюс” или “минус”.
В общем виде первый закон Кирхгофа можно записать как:
Для примера возьмем узел, в котором протекают токи, указанные стрелками (далее рассмотрим это все на конкретных схемах).
Токи, втекающие и вытекающие из узла, берутся с противоположными знаками. Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Будем считать токи положительными, если они втекают в узел, а вытекающие из узла – отрицательными. Тогда первый закон Кирхгофа для узла, представленного на рисунке 2, запишется:
I1-I2+I3+I4=0
Это выражение можно записать и в следующем виде:
I2=I1+I3+I4;
Ток I2 мы перенесли за знак равенства, его знак поменялся на противоположный (был с “минусом”, стал с “плюсом”).
Остальные токи мы не переносим, поэтому их знаки не меняются.
Согласно последнему выражению, первый закон Кирхгофа можно сформулировать по-другому:
Сумма токов, втекающих (подходящих) в узел, равна сумме токов, вытекающих (отходящих) из узла.
Все это говорит о том, что в узле эти токи не остаются и заряд в узле не накапливается.
Для более полного понимания, представим электрическую цепь (схему электрической цепи), для которой запишем первый закон Кирхгофа.
Запишем для этой цепи первый закон Кирхгофа для узла “a” (о том, как определить количество уравнений по первому и второму законам Кирхгофа, рассмотрим в конце ).
I1+I2-I3=0 или I3=I1+I2.
Второй закон Кирхгофа
Этот закон применяется к контурам электрической цепи и выражает баланс напряжений в них. Второй закон Кирхгофа звучит так:
Алгебраическая сумма ЭДС в замкнутом контуре (с учетом направления обхода контура) равна алгебраической (учитывается знак “+” или “-“) сумме падений напряжений на всех сопротивлениях (элементах) этого контура.
Для того, чтобы правильно составить уравнения по второму закону Кирхгофа, нужно пользоваться следующим правилом:
ЭДС берется со знаком “+”, если ее действие совпадает с направлением обхода контура. Напряжение на элементе контура берется со знаком “+”, если направление тока через данный элемент совпадает с направлением обхода контура. Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
Запишем второй закон Кирхгофа для цепи, представленной ниже:
Выбираем направление обхода контура по часовой стрелке. В данном случае направление тока и направление обхода контура совпадают, поэтому I·R1 и I·R2 взяли со знаком “+”. А также совпадает направление обхода контура и действие ЭДС, поэтому ЭДС также записали со знаком “+”.
Возьмем еще один пример.
Запишем для этой цепи второй закон Кирхгофа. Обход выбираем по часовой стрелке (указали обход контура на схеме круговой стрелкой внутри контура). Как видим, направление обхода контура и направление тока I1 совпадают, а ток I2 направлен напротив обхода контура.
Следовательно, падение напряжения на резисторе R1 запишется со знаком “+”, т. е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
Направление действия ЭДС совпадает с обходом контура, поэтому ЭДС E берем со знаком “+”.
Запишем второй закон Кирхгофа для этой цепи:
I1·R1-I2·R2=E
Ну и напоследок рассмотрим сложную электрическую цепь, состоящую из нескольких источников и резисторов.
Введем произвольно направление токов в ветвях, а также укажем на схеме в виде круговых стрелок направление обхода контуров.
Токи в ветвях направили произвольно, обход контура выбрали по часовой стрелке, а также узлы в этой схеме обозначили буквами a и b. Для того, чтобы понять, как и сколько уравнений по первому и второму законам Кирхгофа нужно составить для данной цепи, необходимо посчитать количество ветвей, узлов и независимых контуров.
Подробно вышесказанные понятия электрической цепи мы рассмотрим в следующих статьях. А пока вкратце.
Узел – это место соединения трех и более ветвей в электрической цепи (в данном случае таких узлов два. Это узлы “a” и “b”.
Ветвь – это участок электрической цепи, который образуется одним или несколькими последовательно соединенными элементами и через все эти элементы протекает один и тот же ток.
Контур – это любой замкнутый путь электрической цепи, проходящий по двум или нескольким ветвям.
Так же есть такое понятие как независимый контур.
Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
На рисунке 9 будет три контура, два из которых независимые. Если контур 1 независимый, контур 2 независимый(таким образом все три ветви этой схемы цепи вошли в эти независимые контуры). Тогда контур 3 уже независимым не будет, поскольку все ветви “заняты” остальными двумя контурами.
Или если контур 1 независимый (он включает в себя ветви с элементами E и R1). Контур 3 независимый (он включает в себя ветви с элементом E и ветвь с элементом R3. Элемент R3 ранее не входил в первый независимый контур), поэтому контур 3 считается независимым.
Получается, что все ветви “заняты”. Тогда контур 2 независимым уже не будет, поскольку в него не входят ветви или ветвь ранее не входящую в другие контура. Все ветви вошли в ранее независимые контуры 1 и 3.
В цепи на рисунке 9, в общем случае, три ветви, два узла и два независимых контура. Общее количество уравнений по законам(правилам) Кирхгофа составляется столько, сколько ветвей в схеме цепи за вычетом количества ветвей, где есть источник тока (именно источник тока, а не ЭДС). В нашей схеме нет источников тока, следовательно, составляются три уравнения по законам Кирхгофа. Теперь осталось определить, сколько уравнений нужно составить по первому и второму законам Кирхгофа. Общее количество уравнений будет три. Формула для определения количества уравнений по первому закону Кирхгофа следующая:
N1з.к.=Ny-1, где Ny – количество узлов.
Ny=2, тогда
N1.з.к.=Ny-1=2-1=1
Т. е. по первому закону Кирхгофа составляется одно уравнение для данной цепи, а общее количество уравнений – три. Таким образом, мы получаем, что по второму закону Кирхгофа нужно составить два уравнения. Или для определения количества уравнений по второму закону Кирхгофа есть формула:
N2.з.к.=Nв-(Ny-1), где Nв – количество ветвей
Nв=3, тогда:
N2.з.к.=3-(2-1)=2
По второму закону Кирхгофа составляется два уравнения. Составим систему, состоящую из трех уравнений. Одно уравнение по первому закону Кирхгофа (это уравнение составляется для любого узла a или b) и двух уравнений по второму закону Кирхгофа для двух любых независимых контуров, например, составим для контуров 1 и 2.
Неизвестными в данной системе являются токи I1, I2 и I3. Решая данную систему, находят эти неизвестные.
О том, как решаются задачи с более сложными цепями, мы поговорим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.
Пример сложной электрической цепи вы можете посмотреть на рисунке 1.
Рисунок 1. Сложная электрическая цепь.
Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.
Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Поясню первый закон Кирхгофа на примере рисунка 2.
Рисунок 2. Узел электрической цепи.
Здесь ток I1– ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
I1 = I2 + I3 (1)
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I3 в левую часть выражения (1), тем самым получим:
I1 – I2 – I3 = 0 (2)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
– ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
– напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.
Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.
E1– Е2 = -UR1 – UR2 или E1 = Е2 – UR1 – UR2 (3)
Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).
Расчеты электрических цепей с помощью законов Кирхгофа.
Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.
Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E1=12 в и E2=5 в , с внутренним сопротивлением источников r1=r2=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.
Рисунок 4. Пример расчета сложной электрической цепи.
Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:
I = I1 + I2,
так как I1 и I2 втекают в узел А, а ток I вытекает из него.
Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.
Для внешнего контура:
E1-E2 = Ur1 – Ur2 или E1-E2 = I1*r1 – I2*r2
Для внутреннего левого контура:
E1 = Ur1 + UR или E1 = I1*r1 + I*R
Итак, у нас получилась система их трех уравнений с тремя неизвестными:
I = I1 + I2;
E1-E2 = I1*r1 – I2*r2;
E1 = I1*r1 + I*R.
Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:
I = I1 + I2;
7 = 0,1I1 – 0,1I2;
12 = 0,1I1 +2I.
Далее из первого и второго уравнения выразим ток I2
I2=I – I1;
I2 = I1 – 70;
12 = 0,1I1 + 2I.
Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:
I – I1= I1 – 70;
12 = 0,1I1 + 2I.
Выражаем из первого уравнения значение I
I = 2I1– 70;
И подставляем его значение во второе уравнение
12 = 0,1I1 + 2(2I1 – 70).
Решаем полученное уравнение
12 = 0,1I1 + 4I1 – 140.
12 + 140= 4,1I1
I1=152/4,1
I1=37,073 (А)
Теперь в выражение I = 2I1– 70 подставим значение
I1=37,073 (А) и получим:
I = 2*37,073 – 70 = 4,146 А
Ну, а согласно первому закона Кирхгофа ток I2=I – I1
I2=4,146 – 37,073 = -32,927
Знак «минус» для тока I2 означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I2 вытекает из узла А.
Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.
Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

Для закрепления результатата предлагаю посмотреть подготовленное мной видео:
Содержание:
- Определение и формула ЭДС
- Закон Ома для произвольного участка цепи
- Единицы измерения
- Примеры решения задач
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал
(учтем, что носители тока предполагаются положительными зарядами) постоянно убирались доставляемые током заряды, при этом к концу с
большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны
перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения.
Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи
или на отдельных участках цепи.
Определение и формула ЭДС
Определение
Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется
электродвижущей силой (ЭДС), действующей в цепи или на участке цепи. ЭДС обозначается
$varepsilon$ . Математически определение ЭДС запишем как:
$$varepsilon=frac{A}{q}(1)$$
где A – работа сторонних сил, q – заряд, над которым производится работа.
Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.
ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:
$$varepsilon=oint_{L} bar{E}^{*} d bar{l}(2)$$
где $bar{E}^{*}$ – напряженность поля сторонних сил. Если напряженность поля сторонних
сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по
данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:
$$varepsilon=int_{1}^{2} bar{E}^{*} d bar{l}(3)$$
Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.
Закон Ома для произвольного участка цепи
Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:
$$U_{12}=varphi_{1}-varphi_{2}+varepsilon_{12}(4)$$
где U12=IR21 – падение напряжения (или напряжение) на участке цепи 1-2 (I-сила тока);
$varphi_{1}-varphi_{2}$ – разность потенциалов концов участка;
$varepsilon_12$ – электродвижущая сила, которую содержит участок цепи.
$varepsilon_12$ равна алгебраической сумме ЭДС всех источников, которые находятся на данном участке.
Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в
направлении тока (ток течет от минуса к плюсу источника).
Единицы измерения
Размерность ЭДС совпадает с размерностью потенциала. Основной единицей измерения ЭДС в системе СИ является: [$varepsilon$]=В
1В=1Дж/1Кл
Примеры решения задач
Пример
Задание. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А.
Какова работа, которую совершают сторонние силы за 1 мин?
Решение. В качество основы для решения задачи используем формулу для вычисления ЭДС:
$$varepsilon=frac{A}{q}(1.1)$$
Заряд, который проходит в рассматриваемой цепи за 1 мин. можно найти как:
$$q=I Delta t(1.2)$$
Выразим из (1.1) работу, используем (1.2) для вычисления заряда, получим:
$$A=varepsilon I Delta t$$
Переведем время, данной в условиях задачи в секунды ($Delta t$ мин=60 с), проведем вычисления:
$A=10 cdot 0,4 cdot 60=240$ (Дж)
Ответ. A=240 Дж

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
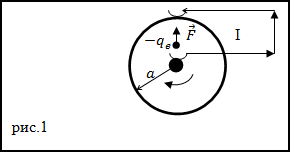
Задание. Металлический диск, имеющий радиус a, вращается с угловой скоростью
$omega$, включен в электрическую цепь при
помощи скользящих контактов, которые касаются оси диска и его окружности (рис.1). Какой будет ЭДС, которая появится между осью
диска и его наружным краем?
Решение. В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила (F)
которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:
$$F=m r omega^{2}(2.1)$$
где m – масса электрона, r – расстояние от оси диска.Fдействует на заряженную частицу (электрон), следовательноучитывая (2.1), имеем:
$$E^{*}=frac{F}{q}=frac{m r omega^{2}}{q}$$
где q – заряд электрона.
В соответствии с формулой, определяющей ЭДС участка цепи, получаем:
$$varepsilon=int_{1}^{2} bar{E} d bar{l}=int_{0}^{a} E^{*} d r=int_{0}^{a} frac{m r omega^{2}}{q} d r=frac{m r omega^{2} a^{2}}{2 q}$$
Ответ. $varepsilon=frac{m r omega^{2} a^{2}}{2 q}$
Читать дальше: Формулы по физике.
На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
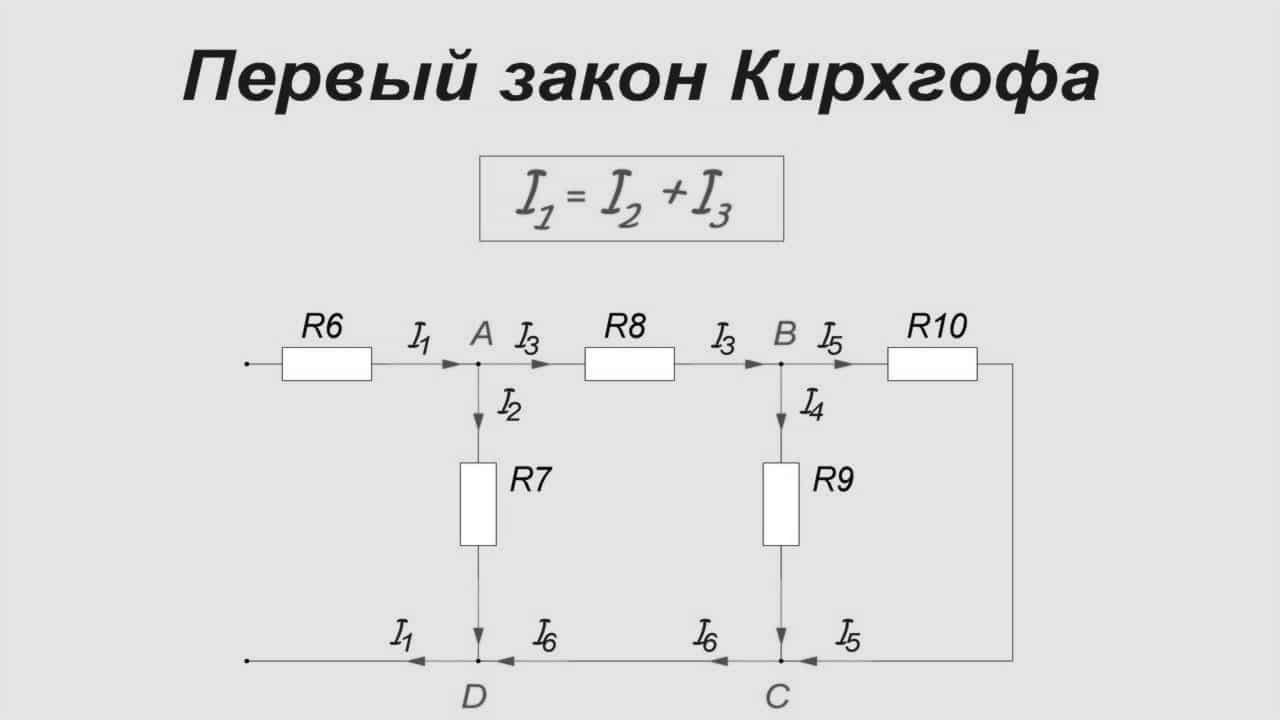
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.
Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.
В частности: ∑Ф=0.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Примеры расчета цепей
Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i1, i2, i3, i4. Из них – два входящие ( i2, i3) и два исходящие из узла (i1, i4). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.
Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i1 + i2 + i3 – i4 = 0.
На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.
Рассмотрим алгоритм решения на примере рис. 5.
Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:
- 1 и 2.
- 1 и 3.
- 2 и 3.
Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I1 + I2 – I3 = 0.
Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.
Пишем уравнения:
- I1R1 + I3 R3 = E1;
- I2R2 + I3R3 = E2.
Решаем систему уравнений:
Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:
Решая эту систему, получим:
- I1 = 1,36 (значения в миллиамперах).
- I2 = 2,19 мА.;
- I3 = 3,55 мА.
Потенциал узла а равен: Ua = I3*R3 = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:
E1 – E2 + I1R1+ I2R2 = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).
Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.
Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.
§ 17. Последовательное и параллельное соединение источников
При последовательном соединении источников общая ЭДС равна алгебраической сумме ЭДС отдельных источников, общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником. ЭДС источника берётся со знаком `«+»`, если направление действия ЭДС совпадает с выбранным направлением. В противном случае ставится знак `«-»`.
При параллельном соединении источников с одинаковыми ЭДС и возможно различными внутренними сопротивлениями общая ЭДС (ЭДС батареи) равна ЭДС одного источника. Внутреннее сопротивление батареи рассчитывается как при параллельном соединении проводников с сопротивлениями, равными внутренним сопротивлениям источников.
При параллельном соединении источников с различными ЭДС выражение для ЭДС батареи усложняется и здесь не приводится.
В схеме на рис. 17.1 $$ {mathcal{E}}_{1}=12$$ В, $$ {mathcal{E}}_{2}=3$$ В, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
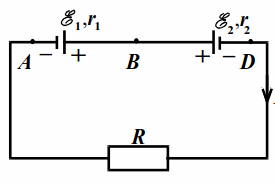 |
| Рис. 17.1 |
Найти напряжения на зажимах источников, т. е. разность потенциалов $$ {varphi }_{A}-{varphi }_{B}$$ и $$ {varphi }_{B}-{varphi }_{D}$$.
ЭДС батареи последовательно соединённых источников:
$$ mathcal{E}={mathcal{E}}_{1}-{mathcal{E}}_{2}=9$$ B.
Причём, полярность батареи совпадает с полярностью источника $$ {mathcal{E}}_{1}$$ т. к. $$ {mathcal{E}}_{1}>{mathcal{E}}_{2}$$.
Ток по закону Ома для замкнутой цепи $$ I=mathcal{E}/(R+{r}_{1}+{r}_{2})=1$$ A. По закону Ома для участков цепи `AB` и `BD`:
$$ {varphi }_{A}-{varphi }_{B}+{mathcal{E}}_{1}=I{r}_{1,}$$, $$ {varphi }_{B}-{varphi }_{D}-{mathcal{E}}_{2}=I{r}_{2}$$.
Отсюда $$ {varphi }_{A}-{varphi }_{B}=I{r}_{1}-{mathcal{E}}_{1}=-11$$ B, $$ {varphi }_{B}-{varphi }_{D}=I{r}_{2}+{mathcal{E}}_{2}=5$$ B.
Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.
Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ {mathcal{E}}_{1}=mathcal{E}$$, $$ {r}_{1}=r·2r/left(r+2rright)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3mathcal{E}$$ и $$ {mathcal{E}}_{1}$$:
$$ {mathcal{E}}_{0}=3mathcal{E}-{mathcal{E}}_{1}=3mathcal{E}-mathcal{E}=2mathcal{E}$$,
$$ {r}_{0}=3r+{r}_{1}=3r+2r/3=11r/3$$.
Ток $$ I={displaystyle frac{{mathcal{E}}_{0}}{R+{r}_{0}}}={displaystyle frac{6mathcal{E}}{3R+11r}}$$.