|
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab |
12 |
N=input(‘N=’);
M=input(‘M=’);
disp(‘Vvod matrici’);
for i=1:N
for j=1:M
a(i,j)=input(”);
end
end
disp(a);
Листинг 9.6. Ввод элементов матрицы
|
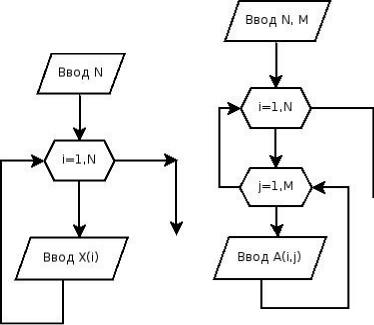
Рис. 9.8.Блок-схема ввода |
Рис. 9.9.Блок-схема |
|
ввода элементов |
|
|
элементов массива |
матрицы |
Алгоритм нахождения суммы состоит в следующем: вначале сумма равна 0 (s=0), затем к s добавляем первый элемент массива и результат записываем опять в переменную s, далее к переменной s добавляем второй элемент массива и результат записываем в s и далее аналогично добавляем к s остальные элементы массива. При нахождении суммы элементов матрицы последовательно суммируем элементы всех строк.
Алгоритм нахождения произведения следующий: на первом начальное значение произведения равно 1 (p=1), затем последовательно умножаем p на очередной элемент, и результат записываем в p.
|
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab |
13 |
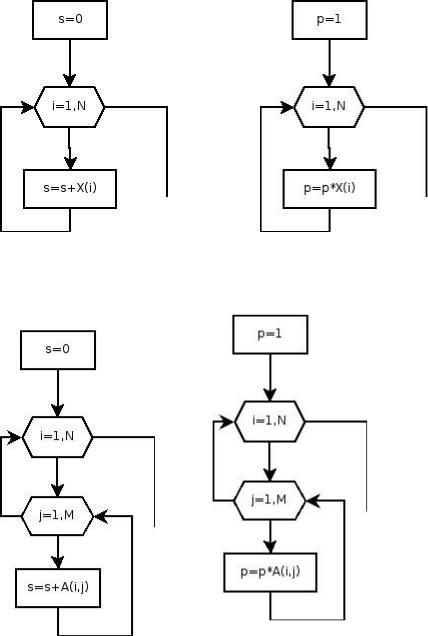
На рис. 9.10, 9.11 приведены блок-схемы алгоритмов нахождения суммы и произведения элементов массива, на рис 9.12, 9.13 – алгоритмы нахождения суммы и произведения элементов матрицы. На листингах 9.7-9.10 представлены элементы программ, реализующие эти алгоритмы.
|
Рис. 9.10. Блок-схема |
Рис. 9.11. Блок-схема |
|
алгоритма |
алгоритма |
|
нахождения суммы |
нахождения |
|
элементов массива |
элементов массива |
|
Рис. 9.12. Блок-схема |
Рис. 9.13.Блок-схема |
|
нахождения |
|
|
нахождения суммы |
произведения |
|
элементов матрицы |
элементов матрицы |
s=0;
for i=1:length(x)
s=s+x(i);
end
Листинг 9.7. Программа вычисления суммы элементов массива
|
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab |
14 |
p=1;
for i=1:length(x)
p=p*x(i);
end
Листинг 9.8. Программа вычисления произведения элементов массива
N=input(‘N=’);
M=input(‘M=’); disp(‘Vvod matrici’); for i=1:N
for j=1:M a(i,j)=input(”); end
end disp(a); s=0;
for i=1:N for j=1:M s=s+a(i,j); end
end
disp(s);
Листинг 9.9. Программа вычисления суммы элементов матрицы
p=1;
for i=1:N
for j=1:M
p=p*a(i,j);
end
end
Листинг 9.10. Программа вычисления произведения элементов матрицы
9.2.3. Поиск максимального (минимального) элемента массива (матрицы)
Пусть в переменной с именем Max хранится значение максимального элемента массива, а в переменной с именем Nmax – его номер. Алгоритм решения задачи поиска максимума и его номера в массиве следующий. Предположим, что первый элемент массива является
|
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab |
15 |
максимальным и запишем его в переменную Max, а в Nmax – его номер (1). Затем все элементы, начиная со второго, сравниваем в цикле с максимальным. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Max, а в переменную Nmax– текущее значение индекса i. Алгоритм нахождения максимального элемента в массиве приведен в блок-схеме на рис. 9.14.
На листинге 9.11 представлен фрагмент программы поиска максимума.
Max=a(1);
Nmax=1;
for i=2:N
if x(i)>Max
Max=x(i);
Nmax=i;
end;
end;
Листинг 9.11. Реализация алгоритма поиска максимума
Алгоритм поиска минимального элемента в массиве будет отличаться от приведенного выше лишь тем, что в условном блоке и, соответственно, в конструкции if текста программы знак поменяется с > на <. На рис. 9.15 представлена блок-схема поиска минимального элемента матрицы и его индексов: Nmin – номер строки, Lmin – номер столбца минимального элемента.
Обратите внимание, что при поиске минимального (максимального) элемента матрицы циклы по i и j начинаются с 1. Иначе при обработке элементов будет пропущена первая строка или первый столбец при сравнении ai,j с min. На листинге 9.12 представлена реализация этого алгоритма.
Min=a(1,1); Nmin=1; Lmin=1;
for i=1:N
for j=1:M
if a(i,j)<Min
Min=a(i,j);
Nmin=i;
Lmin=j;
end; end;
end;
Листинг 9.12. Программа поиска минимального элемента матрицы и его индексов
Соседние файлы в папке про_Scilab
- #
- #
- #
- #
- #
- #
In an interview I was asked if I was given an n*m matrix how to calculate the sum of the values in a given sub-matrix (defined by top-left, bottom-right coordinates).
I was told I could pre-process the matrix.
I was told the matrix could be massive and so could the sub-matrix so the algo had to be efficient. I stumbled a bit and wasn’t told the best answer.
Anyone have a good answer?
ShreevatsaR
38.1k16 gold badges101 silver badges126 bronze badges
asked Feb 17, 2010 at 1:35
4
This is what Summed Area Tables are for. http://en.wikipedia.org/wiki/Summed_area_table
Your “preprocessing” step is to build a new matrix of the same size, where each entry is the sum of the sub-matrix to the upper-left of that entry. Any arbitrary sub-matrix sum can be calculated by looking up and mixing only 4 entries in the SAT.
EDIT: Here’s an example.
For the initial matrix
0 1 4
2 3 2
1 2 7
The SAT is
0 1 5
2 6 12
3 9 22
The SAT is obtained using S(x,y) = a(x,y) + S(x-1,y) + S(x,y-1) – S(x-1,y-1),
where S is the SAT matrix and a is the initial matrix .
If you want the sum of the lower-right 2×2 sub-matrix, the answer would be 22 + 0 – 3 – 5 = 14. Which is obviously the same as 3 + 2 + 2 + 7. Regardless of the size of the matrix, the sum of a sub matrix can be found in 4 lookups and 3 arithmetic ops. Building the SAT is O(n), similarly requiring only 4 lookups and 3 math ops per cell.
Prashant
1573 silver badges13 bronze badges
answered Feb 17, 2010 at 1:42
AlanAlan
4,8872 gold badges23 silver badges17 bronze badges
9
You can do it by Dynamic programming. Create matrix dp with size n*m.
And for each i, j where
1 <= i <= n , 1 <= j <= m
dp[i][j] will be :
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + values[i][j]
And for each query we have lx, rx, ly, ry where lx and rx are top-left coordinates, ly and ry bottom-right coordinates of sub-matrix.
1 ≤ lxi ≤ rx ≤ n, 1 ≤ ly ≤ ry ≤ m
sum = dp[rx][ry] - dp[lx - 1][ry] - dp[rx][ly - 1] + dp[lx-1][ly - 1]
Look at picture to understand how algorithm works.
OD = dp[rx][ry], OB = dp[lx - 1][ry], OC = dp[rx][ly - 1], OA = dp[lx - 1][ly - 1]

answered Jan 26, 2017 at 22:52
1
Create a new matrix where entry (i,j) is the sum of elements in the original matrix that have lower or equal i and j. Then, to find the sum of the elements in the submatrix, you can just use a constant number of basic operations using the corners of the submatrix of your sum matrix.
In particular, find the corners top_left, bottom_left, top_right and bottom_right of your sum matrix, where the first three are just outside the submatrix and bottom_right is just inside. Then, your sum will be
bottom_right + top_left - bottom_left - bottom_right
answered Feb 17, 2010 at 1:41
PeterPeter
126k53 gold badges179 silver badges211 bronze badges
2
Below is a sample implementation in C using Summed Area Tables concept as explained in one of the answers above.
Python implementation for the same can be found at below link –
http://www.ardendertat.com/2011/09/20/programming-interview-questions-2-matrix-region-sum/
#include<stdio.h>
int pre[3][3];
int arr[3][3] = {
{0,1,4},
{2,3,2},
{1,2,7}
};
void preprocess()
{
for(int i=0;i<3;i++)
{
for(int j=0;j<3;j++)
{
if(i>0 && j>0)
{
pre[i][j] = arr[i][j] + pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1];
}
else if(i>0 && j==0)
{
pre[i][j] = arr[i][j] + pre[i-1][j];
}
else if(j>0 && i==0)
{
pre[i][j] = arr[i][j] + pre[i][j-1];
}
else
{
pre[i][j] = arr[i][j];
}
}
}
}
int subsum(int x1, int y1, int x2, int y2)
{
preprocess();
int ans = pre[x2][y2] - pre[x1-1][y2] - pre[x2][y1-1] + pre[x1-1][y1-1];
return ans;
}
int main()
{
printf("%dn",subsum(1,1,2,2));
return 0;
}
answered Apr 19, 2015 at 6:56
learnerlearner
1232 silver badges11 bronze badges
1
This should work. You always have to go through each element in the submatrix to do the addition and this is the simplest way.
*note that the following code may not compile but it’s right in pseudocode
struct Coords{
int x,y;
}
int SumSubMatrix(Coords topleft, Coords bottomright, int** matrix){
int localsum = 0;
for( int i = topleft.x; i <= bottomright.x; i++ ){
for(int j = topleft.y; j <= bottomright.y; j++){
localsum += matrix[i][j];
}
}
return localsum;
}
Edit: An alternative pre-processing method is to create another matrix from the original containing the row or column sums. Here’s an example:
Original:
0 1 4 2 3 2 1 2 7
Row Matrix:
0 1 5 2 5 7 1 3 10
Column Matrix:
0 1 4 2 4 6 3 6 13
Now, just take the endpoint x values and subtract the start point values, like so (for rows based):
for( int i = topleft.y; i >= bottomright.y; i++ ){
localsum += matrix2[bottomright.x][i] - matrix2[topleft.x][i];
}
Now, it’s either O( n ) or O( m )
answered Feb 17, 2010 at 1:40
apanditapandit
3,3041 gold badge26 silver badges32 bronze badges
0
Как найти сумму элементов матрицы
Матрица или массив элементов представляет собой таблицу определенных значений с фиксированным размером в m строк и n столбцов. Множество выполняемых над матрицей и ее элементами операций позволяет решать различные математические задачи. В частности, одной из таких задач является поиск суммы элементов матрицы. Причем рассматриваемые значения могут быть расположенны как по диагонали, так и в других частях заданного математического объекта.

Инструкция
Запишите матрицу размерностью mхn, где m – число строк, а n – число столбцов объекта. В наиболее простом случае поиска суммы всех элементов матрицы выполните последовательное сложение ее значений. В первой строке первый элемент сложите со вторым, к получившемуся результату прибавьте третий и т.д. до последнего значения строки. Далее к сумме элементов первой строки таким же образом прибавляйте значения второй и всех последующих строк матрицы. Причем при сложении чисел учитывайте их знак. Так, значения -4 и 5 дадут в сумме 1, а -5 + -6 = -11.
Определите сумму элементов на главной диагонали заданной матрицы. Главная диагональ матрицы проходит от ее верхнего левого угла до нижнего правого. Все элементы, стоящие на этой «прямой» сложите между собой. Определив сумму всех чисел на главной диагонали, запишите окончательный результат.

Аналогичным образом вычислите сумму элементов на побочной диагонали рассматриваемой матрицы. Побочной диагональю называется «прямая» проходящая от верхнего левого угла матрицы в нижний правый. Все значения объекта, лежащие на данной диагонали, сложите между собой и запишите результат.

Найдите сумму элементов, стоящих ниже главной диагонали. Для этого проведите по главной диагонали матрицы прямую, отсекающую значения самой диагонали и верхней части объекта. Найдите сумму элементов, расположенных ниже прямой. Для этого желательно складывать значения построчно. Из первой строки ниже главной диагонали возьмите единственный стоящий там элемент, сложите его с первым элементом следующей строки, затем к полученной сумме прибавьте значение второго элемента. Далее перейдите к элементам на третьей строке и т.д., пока не будет произведено сложение последнего, не зачеркнутого элемента матрицы ниже главной диагонали.

Для вычисления суммы элементов матрицы, стоящих выше главной диагонали, выполните аналогичные действия, только в качестве слагаемых рассматривайте элементы стоящие выше зачеркнутой диагонали.
Источники:
- как найти элементы побочной диагонали
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Перейти к содержанию
Суммы строк и столбцов матрицы
Просмотров 10.7к. Обновлено 15 октября 2021
Посчитать суммы каждой строки и каждого столбца матрицы. Вывести суммы строк в конце каждой строки, а суммы столбцов под соответствующими столбцами.
Поскольку двумерный массив обычно перебирается построчно, то сумму строк считать проще. Можно, заполняя строку матрицы и выводя ее элементы на экран, накапливать в переменной сумму элементов строки и выводить ее в конце строки.
Для сумм столбцов можно предусмотреть отдельный массив, в ячейках которого накапливать сумму каждого столбца. При построчном проходе по матрице, каждый новый элемент следует суммировать с соответствующим ему элементом массива сумм столбцов. Индекс элемента в строке матрицы будет совпадать с индексом элемента в массиве сумм.
Выводить суммы столбцов следует в отдельном цикле.
Pascal
const
M = 10;
N = 5;
var
a: array[1..N,1..M] of integer;
i, j: byte;
s: integer;
sc: array[1..M] of integer;
begin
for i:= 1 to M do
sc[i] := 0;for i:=1 to N do begin
s := 0;
for j:=1 to M do begin
a[i,j] := random(10);
write(a[i,j]:6);
s := s + a[i,j];
sc[j] := sc[j] + a[i,j]
end;
writeln (' |', s);
end;
for i:= 1 to M do
write('--':6);
writeln;
for i:= 1 to M do
write(sc[i]:6);
writeln;end.
Пример выполнения программы:5 5 7 8 6 8 5 8 4 6 |62
6 3 4 2 8 0 9 2 3 4 |41
7 8 5 4 5 3 9 8 0 3 |52
0 6 0 3 8 9 7 1 8 8 |50
9 4 7 8 4 5 7 6 1 7 |58
-- -- -- -- -- -- -- -- -- --
27 26 23 25 31 25 37 25 16 28
Язык Си
сумма элементов каждого столбца матрицы c++
#include < stdio.h>
#define M 10
#define N 5
main() {
int a[N][M];
int sc[M];
int s, i, j;
srand(time(NULL));
for (i=0; i< M; i++) sc[i] = 0;
for (i=0; i< N; i++) {
s = 0;
for (j=0; j< M; j++) {
a[i][j] = rand() % 10;
printf("%5d", a[i][j]);
s += a[i][j];
sc[j] += a[i][j];
}
printf(" |%dn", s);
}
for (i=0; i< M; i++)
printf("%5s", "--");
printf("n");
for (i=0; i< M; i++)
printf("%5d", sc[i]);
printf("n");
}
Python
сумма элементов строки матрицы python (питон)
from random import random
M = 10
N = 5
a = []
for i in range(N):
b = []
for j in range(M):
b.append(int(random()*11))
print("%3d" % b[j], end='')
a.append(b)
print(' |', sum(b))for i in range(M):
print(" --", end='')
print()for i in range(M):
s = 0
for j in range(N):
s += a[j][i]
print("%3d" % s, end='')
print()
Пример(ы) выполнения программы на языке Python:6 7 3 10 10 10 4 2 6 5 | 63
2 8 0 9 0 4 9 3 6 3 | 44
5 3 1 10 5 6 5 2 0 9 | 46
10 9 10 8 7 8 5 2 10 9 | 78
3 3 6 0 4 1 6 10 10 3 | 46
-- -- -- -- -- -- -- -- -- --
26 30 20 37 26 29 29 19 32 29
В Python используется немного иной алгоритм решения задачи. Сначала создается пустой список - будущая матрица. Далее в цикле в нее добавляются вложенные списки.Суммы строк матрицы вычисляются с помощью функции sum(), которой передается текущий список-строка цикла.
Суммы столбцов вычисляются путем прохода по каждому столбу матрицы. Обратите внимание, что здесь наоборот: внешний цикл - проход по столбцам, внутренний - по строкам.
КуМир
алг суммы строк столбцов
нач
цел M = 10, N = 5
цел таб a[1:N,1:M], sc[1:M]
цел i, j, s
нц для i от 1 до M
sc[i] := 0
кцнц для i от 1 до N
s := 0
нц для j от 1 до M
a[i,j] := int(rand(0,10))
вывод a[i,j], " "
s := s + a[i,j]
sc[j] := sc[j] + a[i,j]
кц
вывод " |", s, нс
кцнц для i от 1 до M
вывод "---"
кц
вывод нс
нц для i от 1 до M
вывод sc[i], " "
кц
кон
Basic-256
M = 10
N = 5
dim a(N,M)
dim sc(M)
for i = 0 to N-1
s = 0
for j=0 to M-1
a[i,j] = int(rand*10)
print a[i,j] + " ";
s = s + a[i,j]
sc[j] = sc[j] + a[i,j]
next j
print " |" + s
next ifor i=0 to M-1
print "-- ";
next i
for i=0 to M-1
print sc[i] + " ";
next i
Как найти сумму элементов матрицы
Матрица или массив элементов представляет собой таблицу определенных значений с фиксированным размером в m строк и n столбцов. Множество выполняемых над матрицей и ее элементами операций позволяет решать различные математические задачи. В частности, одной из таких задач является поиск суммы элементов матрицы. Причем рассматриваемые значения могут быть расположенны как по диагонали, так и в других частях заданного математического объекта.
Запишите матрицу размерностью mхn, где m – число строк, а n – число столбцов объекта. В наиболее простом случае поиска суммы всех элементов матрицы выполните последовательное сложение ее значений. В первой строке первый элемент сложите со вторым, к получившемуся результату прибавьте третий и т.д. до последнего значения строки. Далее к сумме элементов первой строки таким же образом прибавляйте значения второй и всех последующих строк матрицы. Причем при сложении чисел учитывайте их знак. Так, значения -4 и 5 дадут в сумме 1, а -5 + -6 = -11.
Определите сумму элементов на главной диагонали заданной матрицы. Главная диагональ матрицы проходит от ее верхнего левого угла до нижнего правого. Все элементы, стоящие на этой «прямой» сложите между собой. Определив сумму всех чисел на главной диагонали, запишите окончательный результат.
Аналогичным образом вычислите сумму элементов на побочной диагонали рассматриваемой матрицы. Побочной диагональю называется «прямая» проходящая от верхнего левого угла матрицы в нижний правый. Все значения объекта, лежащие на данной диагонали, сложите между собой и запишите результат.
Найдите сумму элементов, стоящих ниже главной диагонали. Для этого проведите по главной диагонали матрицы прямую, отсекающую значения самой диагонали и верхней части объекта. Найдите сумму элементов, расположенных ниже прямой. Для этого желательно складывать значения построчно. Из первой строки ниже главной диагонали возьмите единственный стоящий там элемент, сложите его с первым элементом следующей строки, затем к полученной сумме прибавьте значение второго элемента. Далее перейдите к элементам на третьей строке и т.д., пока не будет произведено сложение последнего, не зачеркнутого элемента матрицы ниже главной диагонали.
Для вычисления суммы элементов матрицы, стоящих выше главной диагонали, выполните аналогичные действия, только в качестве слагаемых рассматривайте элементы стоящие выше зачеркнутой диагонали.
