Как найти сумму геометрической прогрессии учи ру - Сайт, где вы сможете решить свои вопросы

Геометрическая прогрессия – это числовая последовательность, в которой все ее члены расположены в порядке, подчиняющемся определенной закономерности. Формула геометрической прогрессии определяет, что каждое следующее число будет получено умножением предыдущего на знаменатель прогрессии – постоянное число, не меняющее свое значение в пределах одной последовательности.
b_n=b₁ q^(n-1)

В зависимости от знаменателя прогрессии, выписанные члены геометрической прогрессии могут давать различный вид ряда. Если знаменатель является числом положительным, больше 1 (k > 1), тогда он будет увеличивать значение каждого следующего числа. Такая прогрессия будет монотонно возрастать на протяжении всего ряда. Если знаменатель – положительный, но находится между 0 и 1 (0 < k < 1), тогда он будет каждый раз уменьшать значение следующего члена, и такая прогрессия будет называться бесконечно убывающая геометрическая прогрессия.

Если для все возрастающей последовательности, можно только найти сумму первых членов геометрической прогрессии, то сумма членов бесконечно убывающей прогрессии будет равна вполне конкретному числовому значению, которое может рассчитать калькулятор. Третий случай представлен отрицательным знаменателем (k < 0), тогда прогрессия становится знакочередующейся, то есть первые члены геометрической прогрессии определяют порядок знаков для всей последовательности чисел. Как знаменатель геометрической прогрессии, так и первый член геометрической прогрессии по определению не могут быть равны нулю.

Существует всего несколько формул геометрической прогрессии, из которых можно вывести все необходимые для решения конкретных задач:

• Формула первого члена геометрической прогрессии;

• Формула n члена геометрической прогрессии;

• Формула суммы первых членов геометрической прогрессии;

• Формула суммы бесконечно убывающей геометрической прогрессии;

• Формула знаменателя геометрической прогрессии.

Таким образом, если условиями задана геометрическая прогрессия с хотя бы двумя параметрами из всех выше представленных, для нее можно будет найти любую из всех прочих переменных.

Источник

Геометрическая прогрессия

Кусочек теории.

Геометрическая прогрессия – это последовательность чисел, не равных нулю, в которой каждый следующий член, начиная со второго, в одно и то же количество раз больше (или меньше) предыдущего.

Последовательность чисел 2; 4; 8; 16; 32; 64; … будет являться геометрической прогрессией, причем возрастающей, т.к. каждое следующее число больше предыдущего в 2 раза. В данном случае число 2 является знаменателем этой прогрессии.

Также геометрической прогрессией будет являться последовательность чисел 12; 6; 3; 1,5; 0,75; 0,375; … , причем убывающей, т.к. в ней числа уменьшаются в 2 раза. Но геометрическую прогрессию прежде всего связывают с умножением, поэтому правильнее сказать, что в последовательности числа увеличиваются в 0,5 раз. Здесь знаменателем будет число 0,5.

Знаменатель геометрической прогрессии обозначают буквой q. Если знаменатель не дан, то найти его можно делением текущего члена прогрессии на предыдущий:

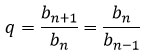
Найти любой по счету член геометрической прогрессии можно, зная ее первый член и знаменатель. Запишем формулу n-ого члена:

Но необязательно знать именно первый член прогрессии. Пригодится может любое по счету число. Только тогда формула чутка изменится:

И держи третью формулу для нахождения n-ого члена геометрической прогрессии через предыдущий и последующий члены (правда по модулю)!

Помимо этих трех формул пригодится еще формула суммы:

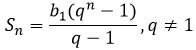
Практика.

Задание 1.

Это задание можно решить без формул. Но если уж так хочется, то можно и по формулам, но мне вот не хочется)

Откинем пока минусы…

Если разделить 125 на 100, то мы увидим во сколько раз следующее число меньше предыдущего: в 1,25 раз. То же самое число получится, если 100 разделить на 80.

Найдем 4-ое число в этой последовательности: 80 : 1,25 = 64.

И 5-ое: 64 : 1,25 = 51,2.

Но не забываем, что знаки у чисел чередуются: четвертое число будет отрицательным, а пятое – положительным.

Ответ: 51,2.

Задание 2.

Опять знаки у чисел чередуются, значит число, спрятанное под иксом, будет отрицательным.

Не будем морочить голову формулами, пойдем задом наперед: разделим 4-ое число на 3-ое (найдем знаменатель прогрессии):

96 : 24 = 4 (знаки у чисел мы откинули временно).

Значит, чтобы найти икс надо 24 разделить на знаменатель 4 и взять результат с минусом.

Ответ: -6.

Задание 3.

По данной нам в условии задаче формуле можно сразу понять, что 2 – знаменатель прогрессии. Если это не понятно – вот доказательство:

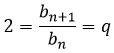
Здесь схитрить не получится, поэтому используем формулу и находим b₆.

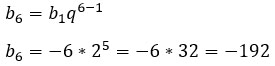
Ответ: -192.

Задание 4.

Каждое следующее число в 4 раза больше предыдущего, значит знаменатель q равен 4.

Зная первый член прогрессии и знаменатель можно найти сумму первых шести членов (n = 6).

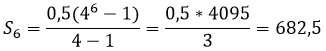
Ответ: 682,5.

Задание 5.

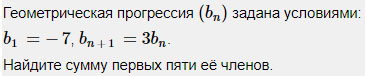
Похожее условие уже встречалось в задании 3. Из данной формулы делаем вывод, что знаменатель q = 3.

Находим сумму:

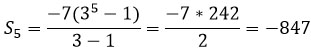
Ответ: -847.

Вот и всё!

С наилучшими пожеланиями, твой персональный препод)

Источник

запиши периодическую дробь (0,(8)) обыкновенной дробью.

Решение.

Достаточно очевидно, что (0,(8)=0,8+0,08+0,008+…) Слагаемые в правой части равенства образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен (0,8), знаменатель равен (0,1). Найдём сумму по формуле:

S=b11−q=0,81−0,1

Осталось выполнить нужные действия с десятичными дробями:

0,81−0,1=0,80,9=89

Таким образом, бесконечная периодическая десятичная дробь (0,(8)) обращается в обыкновенную дробь (8/9).

Ответ: (0,(8)=8/9).

Источник

16
Июл 2013

Категория: Справочные материалы

Геометрическая прогрессия

2013-07-16
2021-06-28

А вы знаете удивительную легенду о зернах на шахматной доске? + показать

Определение

Геометрическая прогрессия — последовательность чисел (членов прогрессии) , в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии):

, где

Например, последовательность 1, 2, 4, 8, 16, … – геометрическая ()

Геометрическая прогрессия

Знаменатель геометрической прогрессии

$q=frac{b_{k+1}}{b_k}$ ,

Характеристическое свойство геометрической прогрессии

$b_n^2=b_{n-1}cdot b_{n+1}$ для

Последовательность является геометрической тогда и только тогда, когда для любого n > 1 выполняется указанное выше соотношение.

В частности, для геометрической прогрессии с положительными членами, верно: $b_n=sqrt{b_{n-1}cdot b_{n+1}}$

Формула n-го члена геометрической прогрессии

$b_n=b_1cdot q^{n-1}$

Сумма n первых членов геометрической прогрессии

$S_n=frac{b_1(q^n-1)}{q-1}$ , где

(если же , то )

Бесконечно убывающая геометрическая прогрессия

При , геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число $S=lim_{nto infty}S_n$ и $S=frac{b_1}{1-q}$

Посмотри это видео

Примеры

Пример 1. Последовательность {} –геометрическая прогрессия.

Найдите , если $b_6=-frac{1}{81}$ , $q=-frac{1}{9}.$

Решение: + показать

Приметр 2. Найдите знаменатель геометрической прогрессии {}, в которой $b_8=172,;b_{11}=2frac{11}{16}.$

Решение: + показать

Пример 3. Найдите девятый член геометрической прогрессии, если ее десятый член равен , а одиннадцатый член равен

Решение: + показать

Пример 4. Найдите сумму первых шести членов геометрической прогрессии

Решение: + показать

Пример 5. Найдите сумму первых пяти членов геометрической прогрессии {}, в которой $b_3=frac{1}{2},;b_5=2,;q>0.$

Решение: + показать

Пример 6. Представьте в виде обыкновенной дроби число

Решение: + показать

Пример 7. Найдите , если известно, что числа являются последовательными членами геометрической прогрессии (в указанном порядке).

Решение: + показать

Пример 8. Найдите знаменатель геометрической прогрессии, отношение суммы первых четырех членов которой, к сумме первых двух членов равно $frac{82}{81}.$

Решение: + показать

Пример 9. Между числами и вставьте три числа так, чтобы получилась геометрическая прогрессия

Решение: + показать

Вы можете пройти тест по теме «Геометрическая прогрессия»

Автор: egeMax |

комментариев 5

Печать страницы

Источник

Сумма членов геометрической прогрессии находится по одной из формул:

Формулы суммы членов геометрической прогрессии

1) {S_n= frac{b_1-b_1 cdot q^n}{1-q}},

2) {S_n= frac{b_1 cdot (1-q^n)}{1-q}}

b₁ – первый член прогрессии,

q – знаменатель прогрессии,

n – номер члена

Для нахождения суммы членов геометрической прогрессии вы можете воспользоваться нашим онлайн калькулятором. Просто введите данные и получите результат. А узнать больше про геометрическую прогрессию можно на странице.

Пример нахождения суммы арифметической прогрессии

Задача 1

Дана арифметическая прогрессия: 1; 3; 9; … Найдите сумму первых восьми ее членов.

Решение

Первый член прогрессии b₁ = 1.

Чтобы найти знаменатель прогрессии, нужно разделить ее второй член на первый. В нашем случае q = b₂ / b₁ = 3 / 1 = 3.

Количество суммируемых членов равно 8, т. е. n = 8. Подставим значения в формулу и получим результат:

S_n= dfrac{b_1 cdot (1-q^n)}{1-q} = dfrac{1 cdot (1-3^8)}{1-3} = dfrac{1 cdot (1-6561)}{-2} = dfrac{-6560}{-2} = 3280

Ответ: 3280

Используем калькулятор для проверки.

Источник

Геометрическая прогрессия

Геометрическая прогрессия

Формулы суммы членов геометрической прогрессии

Пример нахождения суммы арифметической прогрессии

Вам также может понравиться

Как найти календарь в смартфоне самсунг

Как найти где находится посылка почта

Как найти свою целостность

Добавить комментарий Отменить ответ