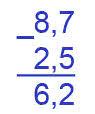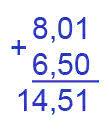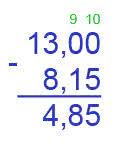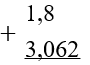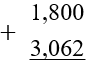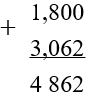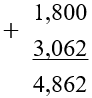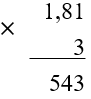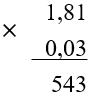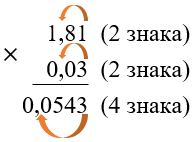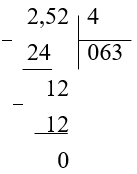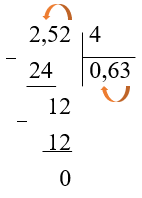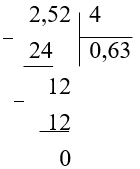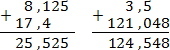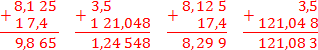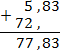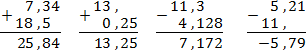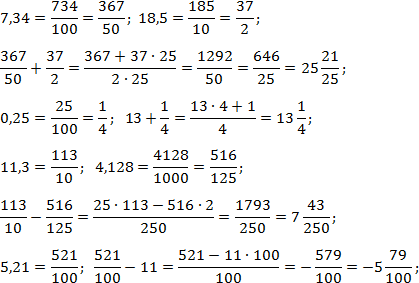Как найти сумму или разность десятичных дробей

Десятичные дроби и действия с ними

Десятичная дробь – это дробь, имеющая в знаменателе 10, 100, 1000 и т.д.

Такие дроби принято записывать в строчку, а не как обыкновенную дробь.

ЗАПИСЬ ДЕСЯТИЧНОЙ ДРОБИ:

1. Сначала выделяют целую часть, ставят запятую, а потом записывают числитель дробной части.

Например:

(7frac{38}{100} = 7,38)

1. Если дробь правильная, то целая часть равна 0:

Например:

(frac{6}{10} = 0,6)

1. После запятой должно стоять столько цифр, сколько нулей стоит после единицы в знаменателе дроби. Например, если в знаменателе 10, то после запятой будет одна цифра.

2. Если в знаменателе 1000, то после запятой должно быть три цифры. Если в числителе дроби цифр меньше, чем нулей в знаменателе, тогда после запятой ставят нужное количество нулей, а уже потом записывают числитель:

Например:

(frac{56}{1000})

в знаменателе три нуля, а в числителе только две цифры. Чтобы уравнять количество цифр и нулей, представим дробь как

(frac{056}{1000})

Ноль в начале числителя никак на него не влияет, но помогает нам записать дробь в виде десятичной. Получается, что:

(frac{56}{1000} = frac{056}{1000} = 0,056)

ЧТЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ:

1. Читают десятичные дроби в соответствии с количеством цифр после запятой. Если цифра одна, то знаменатель соответствует числу 10. Тогда мы говорим, что доля десятичная. Если цифры две, то знаменатель соответствует числу 100, доля такой дроби – сотая. Так же называют тысячную долю, десятитысячную, миллионную и так далее.

Например:

(19frac{32}{100} = 19,32) – девятнадцать целых, 32 сотых;

(2frac{9}{1000} = 2frac{009}{1000} = 2,009) – две целых, 9 тысячных;

(frac{3}{10} = 0,3) – три десятых.

1. Если приписать или убрать ноль в конце дроби, то она не изменится.

Например:

(0,80 = 0,8) (80 сотых = 8 десятых);

(0,0780 = 0,078) (780 десятитысячных = 78 тысячных).

СРАВНЕНИЕ ДСЯТИЧНЫХ ДРОБЕЙ:

Чтобы сравнить дроби, их нужно привести к одинаковому количеству знаков после запятой.

Например:

Сравним 0,07 и 0,5.

У первой дроби после запятой две цифры, у второй только одна. Значит второй дроби нужно ее добавить так, чтобы дробь не изменилась. Мы можем приписать ноль в конце дроби.

Получим 0,07 и 0,50. Теперь мы сравниваем две дроби со знаменателем 100. Становится понятно, что 7<50, значит 0,07<0,50, значит 0,07<0,5.

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:

Сложим две десятичные дроби:

(1,8 + 3,062)

СПОСОБ 1:

1. Чтобы найти сумму или разность десятичных дробей, можно представить их как обыкновенные.

(1frac{8}{10} + 3frac{62}{1000})

1. Если дроби имеют разные знаменатели, приведем их к одному. Проще всего приписать к одной дроби (и к числителю, и к знаменателю) одинаковое количество недостающих нулей:

(1frac{800}{1000} + 3frac{62}{1000})

1. Теперь сложим дроби как смешанные:

(1frac{800}{1000} + 3frac{62}{1000} = 4frac{800 + 62}{1000} = 4frac{862}{1000})

1. Переведем дробь обратно в десятичную:

(4frac{862}{1000} = 4,862)

СПОСОБ 2:

1. Сумму или разность десятичных дробей можно найти столбиком. Запишем одно число под другим так, чтобы запятая одной дроби находилась по запятой другой:

1. Уравняем количество знаков (чисел) после запятой:

1. Сложим числа в столбик не обращая внимание на запятую.

1. Поставим запятую суммы под запятыми слагаемых:

СПОСОБ 3:

Можно воспользоваться тем фактом, что число состоит из целой и дробной частей и сложить сначала одно, потом другое.

1. Представим дроби в ином виде:

(1,8 = 1 + 0,8)

(3,062 = 3 + 0,062)

1. Сложим целые части:

(1 + 3 = 4)

1. Сложим дробные части:

(0,8 + 0,062 = 0,862)

1. Сложим полученные значения:

(4 + 0,862 = 4,862)

УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:

Умножение десятичной дроби на натуральное число:

Например:

(1,81 bullet 3)

1. Чтобы умножить десятичную дробь на число, нужно найти их произведение в столбик, не обращая внимания на запятую:

2. В полученном произведении отделить запятой столько знаков справа, сколько отделено у дроби:

Умножение десятичной дроби на десятичную дробь:

Например:

(1,81 bullet 0,03)

1. Чтобы умножить десятичную дробь на десятичную, нужно найти их произведение в столбик, не обращая внимания на запятую:

1. В полученном произведении отделить запятой столько знаков справа, сколько в сумме отделено у множителей:

Умножение десятичной дроби на 10, 100, 1000 и т.д.:

Чтобы умножить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков вправо, сколько нулей стоит в множителе после единицы.

Например:

(2,34 bullet 10 = 23,4)

(0,687 bullet 1000 = 687)

(7,095 bullet 100 = 709,5)

Умножение десятичной дроби на 0,1, 0,01, 0,001 и т.д.:

Чтобы умножить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков влево, сколько знаков отделяет запятая в множителе:

(183,7 bullet 0,01 = 1,837)

(0,22 bullet 0,1 = 0,022)

(619 bullet 0,001 = 0,619)

ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:

Деление десятичной дроби на число:

Например:

(2,52 : 4)

1. Найдем частное в столбик, не обращая внимание на запятую:

1. В полученном частном отделим запятой столько знаков справа, сколько отделяется в делимом:

Деление десятичной дроби на десятичную дробь:

Например:

(0,252 : 0,4)

1. В делителе и делимом перенести вправо запятую на столько знаков, сколько их после запятой в делителе.

(0,252 : 0,4 = 2,52 : 4)

1. Выполнить деление на натуральное число.

Деление десятичной дроби на 10, 100, 1000 и т.д.:

Чтобы разделить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков влево, сколько знаков отделяет запятая в множителе.

• Разделить на 10 = умножить на 0,1

• Разделить на 100 = умножить на 0,01

• Разделить на 1000 = умножить на 0,001

Деление десятичной дроби на 0,1, 0,01, 0,001 и т.д.:

Чтобы разделить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков вправо, сколько нулей стоит в множителе после единицы.

• Разделить на (0,1 =) умножить на 10

• Разделить на( 0,01 =) умножить 100

• Разделить на (0,001 = )умножить на 1000

Сложение и вычитание десятичных дробей

15 августа 2011

Чтобы найти сумму или разность двух чисел, записанных в десятичной форме, надо выполнить три шага:

1. Записать числа в столбик таким образом, чтобы соответствующие разряды совпадали. Главный ориентир — десятичные точки. Они не являются отдельным разрядом, но должны стоять на одной вертикали;
2. Сложить или вычесть полученные дроби столбиком — подобно тому, как мы складываем и вычитаем обычные числа. Не забудьте «внедрить» десятичную точку между соответствующими разрядами;
3. Полученное число и будет ответом — больше ничего делать не надо.

Как видите, сложение десятичных дробей почти ничем не отличается от сложения обычных чисел. Самое сложное — правильно сопоставить разряды слагаемых, чтобы десятичные точки находились на вертикальной прямой, друг под другом.

Задача. Найдите значение выражений: 8,125 + 17,4; 3,5 + 121,048.

Для каждого выражения приведем правильную запись и две неправильные (самые распространенные). Сначала — правильные:

Теперь рассмотрим неправильные решения. В первом случае все числа «прижаты» к левому краю, во втором — к правому. Ответы получатся совсем другие:

Как видите, ничего общего с тем, что должно получиться на самом деле.

Если в одном из слагаемых нет десятичной точки, ее ставят справа от всего числа. Например, возьмем числа 5,83 и 72. В этом случае операция сложения будет выглядеть так:

Кто-то скажет, что все эти отступы, сдвиги и запятые — ненужные сложности, и лучше работать «по старинке». Что ж, я никого не собираюсь переубеждать. Отмечу лишь, что новая технология всегда требуют более высокой квалификации от тех, кто собирается ее использовать. В этом плане десятичные дроби — следующий уровень развития после обычных.

Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25; 11,3 − 4,128; 5,21 − 11.

Эти примеры показывают, насколько упрощаются вычисления, когда дроби записаны в десятичной форме. Никаких дополнительных множителей, никаких общих знаменателей.

Чтобы почувствовать разницу, решим ту же задачу традиционным методом. Для этого переведем все десятичные дроби в обычные. Взгляните:

Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25; 11,3 − 4,128; 5,21 − 11.

Итак, переводим все десятичные дроби в обычные и считаем по классической схеме:

Мы специально не стали выполнять обратный переход — от обычной дроби к десятичной — чтобы немного сократить вычисления.

Видно, что длина решения выросла многократно. Поэтому старайтесь работать с десятичными дробями везде, где это возможно.

Смотрите также:

1. Умножение и деление десятичных дробей
2. Как представить обычную дробь в виде десятичной
3. Локальная теорема Муавра — Лапласа
4. Вебинар по заданию 13: тригонометрия
5. Задача B4: тарифы на сотовую связь
6. Логарифмические неравенства, сводящиеся к квадратным

Сложение и вычитание десятичных дробей

Тема: Сложение и вычитание десятичных дробей

Чтобы научиться правильно выполнять сложение десятичных дробей, достаточно выучить правило, состоящее всего из трех слов.

Три слова такие: запятая под запитой. Это самое важное, что следует помнить при сложении десятичных дробей. Складывая десятичные дроби, мы записываем их так, чтобы запятые в слагаемых находились строго одна под другой. Если после запятой в одном слагаемом цифр меньше, чем в другом, можно недостающие цифры дополнить нулями (а можно и не делать этого). В остальном сложение десятичных дробей практически ничем не отличается от сложения натуральных чисел — темы, которую проходили еще в начальной школе.

Запомните!

Если исходные десятичные дроби имеют разное количество знаков (цифр) после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.

Итак, ещё раз коротко основные правила сложения:

• уравниваем количество знаков после запятой;
• записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом;
• выполняем сложение десятичных дробей, не обращая внимания на запятые, по правилам сложения в столбик натуральных чисел;
• ставим в ответ запятую под запятыми.

Рассмотрим на примерах, как происходит сложение десятичных дробей.

 Чтобы сложить 5,7 и 6,8, записываем их запятая под запятой. Затем складываем цифры по разрядам и в полученном ответе сносим запятую все по тому же правилу — запятая под запятой.

 При сложении 2,256 и 0,74 числа записываем так, чтобы запятая находилась под запятой. Поскольку во втором числе после запятой два знака, а в первом — три, недостающий один знак в конце второго числа дополняем нулем (но его можно и не писать). После этого складываем числа, не обращая внимания на запятую (то есть к 2256 прибавляем 740). В результате сносим запятую (ровно под запятой слагаемых).

 Как обычно, сложение десятичных дробей начинаем с их записи таким образом, чтобы запятая стояла точно под запятой. Первым удобнее записать число, у которого количество цифр после запятой больше. Чтобы уравнять количество знаков после запятой в обоих слагаемых, во втором третьей цифрой после запятой записываем нуль. Складываем 52462 и 4980, не обращая внимания на запятую. В ответе сносим запятую под запятой.       

 Чтобы сложить десятичные дроби, записываем их «запятая под запятой». Складываем 4821 и 3179, не обращая внимания на запятую. После этого сносим запятую под запятой. Поскольку в десятичной дроби после запятой нули на конце не пишут, окончательный ответ 8.

 Чтобы к натуральному числу прибавить десятичную дробь, можно в записи натурального числа в конце приписать запятую и столько нулей, сколько нужно (в данном примере — три). Затем складываем 35000 и 3146 и сносим запятую.

 Сложение начинаем с записи десятичных дробей по правилу «запятая под запятой». Затем недостающий знак после запятой у числа 8,3 дополняем нулем. Складываем 374 и 830. В ответ сносим запятую под запятой.

Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.

Правило вычитания десятичных дробей

1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!

Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.

2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.

3) Вычитаем числа, не обращая внимания на запятую.

4) Сносим запятую под запятыми.

Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:

9,7-3,5=6,2.

Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой. Так как у 23,45 после запятой две цифры, а у 1,5 — только одна, дописываем в 1,5 нуль. После этого ведем вычитания, не обращая внимания на запятую. В результат сносим запятую под запятыми:

23,45 — 1,5=21,95.

Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:

63,5-8,921=54,579.

Задания для самостоятельного решения:

1. Вычислите:

а) 10,3 – 8,17;   б) 9,432 – 8,32;   в) 7,3 + 0,865;

г) 4,1 – 2,74;     д) 2,031 – 1,05;    е) 3,6 + 0,55

2. Выполните сложение:

1,08 + 5,1 + 0,988 = 

3. Решите уравнение:

х +3,72 = 8

4. Вычислите выражение:

12,36 + ((11,31 + 0,03) – 1,38) – 3, 04 = 

5. Решите задачу:

В первый день магазин продал 87,5 кг сахара, а во второй – на 9,85 кг больше. Сколько килограммов сахара продал магазин за два дня?

Вы уже умеете складывать обыкновенные дроби с равными знаменателями. Научимся складывать десятичные дроби. Найдем сумму 2,374 + 1,725. Обратив эти дроби в обыкновенные, получаем:

$2,374 + 1,725 = 2frac{374}{1000} + 1frac{725}{1000} = 3 + frac{374 + 725}{1000} = 3 + frac{1099}{1000} = 3 + 1frac{99}{1000} = 4frac{99}{1000} = 4,099$

Однако складывать десятичные дроби можно гораздо проще, не обращая их в обыкновенные. 

Сходство способов записи десятичных дробей и натуральных чисел позволяет выполнять сложение десятичных дробей в столбик.

Чтобы сложить две десятичные дроби, надо:

1) уравнять в слагаемые количество цифр после запятой;

2) записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;

3) сложить полученные числа так, как складывают натуральные числа;

4) поставить в полученной сумме запятую под запятыми в слагаемых.

На рисунках 207 + 208 показано, как найти суммы 2,374 + 1,725 и 7,6 + 11,35.

В столбик можно также вычитать десятичные дроби.

Чтобы из одной десятичной дроби вычесть другую, надо:

1) уравнять в уменьшаемом и вычитаемом количество цифр после запятой;

2) записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;

3) произвести вычитание так, как вычитают натуральные числа;

4) поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.

На рисунке 209 показано, как найти разность 0,8 − 0,593.

Из приведенных примеров видно, что сложение и вычитание десятичных дробей выполнялось поразрядно, т.е. так, как мы производили соответствующие действия с натуральными числами. Это и есть главное преимущество десятичной формы записи дробей.

Свойства сложения натуральных чисел выполняются и для дробных чисел. Напомним эти свойства.

a + b = b + a − переместительное свойство сложения,

(a + b) + c = a + (b + c) − сочетательное свойство сложения.

Пример 1. Вычислите разность 4 км 36 м − 768 м, записав данные величины в километрах.

Решение. Имеем:

$4 км 36 м – 768 м = 4frac{36}{1000} км – frac{768}{1000} км = 4,036 км – 0,768 км = 3,268 км.$

Ответ: 3,268 км.

Пример 2. Собственная скорость катера равна 30 км/ч, а скорость течения реки − 1,4 км/ч. Найдите скорость катера по течению и его скорость против течения реки.

Решение.

1) 30 + 1,4 = 31,4 (км/ч) − скорость катера по течению.

2) 30 − 1,4 = 28,6 (км/ч) − скорость катера против течения.

Ответ: 31,4 км/ч, 28,6 км/ч.