Как найти сумму измеренных углов

Выполнить
камеральную обработку результатов
теодолитной съемки:

–
выполнить математическую обработку
теодолитного полигона,

–
составить план по координатам в масштабе
1 : 5000.

Исходные
данные. Координаты точки 1 принять: X₁
= 150,00 м, У₁
= 200,00 м. Остальные данные взять согласно
варианту в табл. 1 и 2 , рис. 3.

Математическая
обработка
теодолитного полигона

Выписать
в
«Ведомость
вычисления
координат»
(приложение
1) исходные данные: измеренные углы,
длины сторон; дирекционный угол
направления 1 – 2, координаты точки 1 (X₁,
У₁).

Контроль: выписку
данных считать с заданием.

Порядок работы
рассмотрим на примере (приложение 1).

1. Подсчитать сумму измеренных углов:

∑β_изм
= β₁+
β₂
+
. . . + β_n.

В графе
2 сумма измеренных углов равна –

∑β_изм
= β₂
+
β₃
+
. . . + β₆
+ β₁
= 86^о34′
+ 132^о42′
+ . . . + 158^о18′
+ 120^о57′
= 719^о58′.

2. Теоретическая сумма углов полигона:

∑β_т
= 180° (n—2),

где n
– количество углов полигона.

∑β_т
=
180° (6—2) =720°00′.

3. Вычислить угловую невязку полигона:

f_β
= ∑β_изм
– ∑β_т
=
719°58′ — 720°00′ = — 0°02′.

4. Вычислить предельную (допустимую) угловую невязку:

Пред.
f_β
= ± 1,′5 √n

Пред.
f_β
= ± 1,′5 √6
=
± 3′,6.

– 02′ < – 3′,6 –
невязка допустима.

Если невязка хода
оказалась допустимой, т. е. меньше
предельной (02′ < 3′,6), то ее распределяют
с обратным знаком по 01′ в углы с короткими
сторонами и вычисляют увязанные углы
(гр. 3).

Таблица 1

Исходные
данные к заданию 1

Измеренные правые
по ходу углы и горизонтальные проложения
сторон полигона

№ вершин измеренных углов (β) и сторон полигона (d)	Варианты
00-09	10-19	20-29	30-39	40-49	50-59	60-69	70-79	80-89	90-99
1 2 3 4 5 1
1-2 2-3 3-4 4-5 5-1	523,88 400,46 562,66 430,34 523,73	535,30 532,76 472,97 469,47 458,64	437,17 547,73 509,92 411,53 455,07	381,53 521,67 497,82 602,62 374,75	453,12 539,93 531,41 544,46 334,14	452,36 490,64 397,02 508,93 417,08	436,39 474,32 548,78 384,24 533,33	458,70 623,08 461,44 440,78 434,82	364,54 554,11 394,02 639,28 468,32	453,,02 293,63 367,48 482,24 417,99

Примечание.
Номер варианта соответствует двум
последним цифрам шифра студента.

Контроль:
– сумма увязанных углов должна равняться
теоретической сумме углов.

∑β_у
= ∑β_т
= 720^о
00′, (в гр. 3 ∑β_у
= 720^о
00′).

5.
Вычислить дирекционные углы.
Дирекционные углы вычисляют последовательно
один за другим (гр. 4), взяв за исходный
α_1,2,
по формуле:

α_к+1
= α_к
+ 180^о
– β_к+1,

где
α_к
и α_к+1
– предыдущий и последующий дирекционные
углы,

β_к+1
– последующий увязанный угол.

Исходный
дирекционный угол α_1,2
берем из таблицы 2 по вариантам.

Таблица 2

Исходные данные
к заданию 1

Дирекционный угол
линии 1-2 (α_1,2)

Вариант	Учебный год
2010/11	2011/12	2012/13	2013/14
0
1
2
3
4
5
6
7
8
9

Примечание.
Данные брать в столбце на соответствующий
текущий учебный год по последней цифре
шифра студента.

Проследим на
примере (гр. 4, 3).

Дирекционные
углы последующих направлений будут:

α
_1,2 = 103^о
06′

α_2,3
= 103^о
06′ + 180^о00′
= 283^о
06′ – 86^о34′
= 196^о32′

α_3,4
= 196^о
32′ + 180^о00′
= 376^о
32′ – 132^о42′
= 243^о50′

α_4,5
= 243^о
50′ + 180^о00′
= 423^о
50′ – 137^о51′
= 285^о59′

α_5,6
= 285^о
59′ + 180^о00′
= 465^о
59′ – 83^о37′
= 22^о22′

α_6,1
= 22^о
22′ + 180^о00′
= 202^о
22′ – 158^о19′
= 44^о03′

Контроль:

α_1,2
= 44^о
03′ + 180^о00′
= 224^о
03′ – 120^о57′
= 103^о06′

6.
Дирекционные углы перевести в румбы
по формулам, при записи перед градусной
мерой угла ставят название румба и
двоеточие, например: СВ : 44°03′.

7.
Вычислить приращения координат по
формулам

∆Х = d∙cos
r,
∆У = d∙sin
r

Предварительно
надо проставить в свои графы знаки
приращений координат согласно румбам.
Приращения координат можно вычислить
с использованием пятизначных таблиц
натуральных значений тригонометрических
функций пли с использованием таблиц
приращений координат или логарифмов.

8.
Подсчитать линейные невязки по приращениям
координат,
для этого удобно сначала просуммировать
положительные и отрицательные их
значения раздельно, а затем найти их
алгебраическую разность. Теоретическая
сумма приращений в замкнутом полигоне:

∑ ∆Х
= О; ∑
∆У
=О.

Значения, отличные
от нуля, будут являться невязками:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Была ли эта статья полезной?

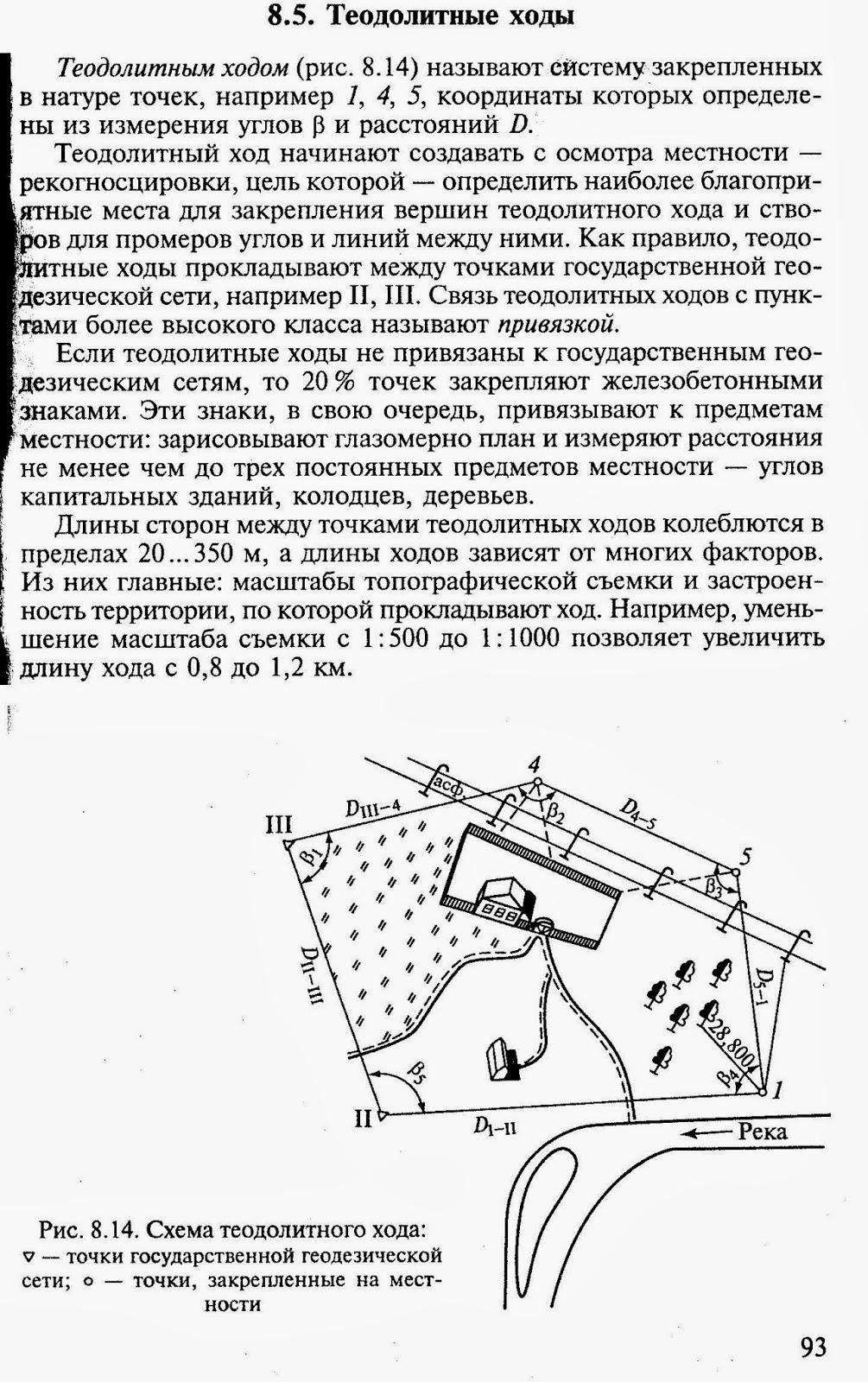
Теодолитным ход – это система закрепленных в натуре точек, например 1,
4, 5, координаты которых определе­ны из измерения углов В и расстояний D.

Теодолитный ход начинают создавать с осмотра местности —
рекогносцировки, цель которой — определить наиболее благопри­ятные места для
закрепления вершин теодолитного хода и створов для промеров углов и линий между
ними. Как правило, теодолитные ходы прокладывают между точками государственной
гео­дезической сети, например II, III.
Связь теодолитных ходов с пунк­тами более высокого класса называют привязкой.

Если теодолитные ходы не привязаны к государственным гео­дезическим
сетям, то 20 % точек закрепляют железобетонными знаками. Эти знаки, в свою
очередь, привязывают к предметам местности: зарисовывают глазомерно план и
измеряют расстояния не менее чем до трех постоянных предметов местности — углов
капитальных зданий, колодцев, деревьев.

Длины сторон между точками теодолитных
ходов колеблются в пределах 20…350 м, а длины ходов зависят от многих
факторов. I Из
них главные: масштабы топографической съемки и застроенность территории, по
которой прокладывают ход. Например, уменьшение масштаба съемки с 1:500 до
1:1000 позволяет увеличить I длину хода с 0,8 до 1,2 км.

 

Схема теодолитного хода

Если производят съемку в масштабе 1:2000, то на застроенной
территории длина хода допускается до 2 км, а на незастроенной — до 3 км.

После того
как выбраны и закреплены вершины сторон теодо­литного хода, производят
измерения сторон и горизонтальных углов.

Общепринятая
погрешность измерения сторон в теодолитных ходах от 1:1000 до 1:2000. Это
означает, что если, например, из­мерена линия длиной 154 м, то при заданной
предельной относи­тельной погрешности измерения 1:1000 результат измерения «пря­мо»
может отличаться от результата измерения «обратно» не бо­лее чем на 154 м /1000 = 15 см. Результаты измерений
записывают в таблицу.

Измерение
горизонтальных углов между точками теодолитного хода (либо левые, либо правые
по ходу продвижения) выполня­ют теодолитами.

В
зависимости от применяемых теодолитов правильность из­мерений контролируют по
разности углов между полуприемами П и Л.

В журнале измерения горизонтальных углов часть места
отводят для схематической зарисовки (абриса) положения точек теодо­литного хода
и пояснительных записей. Аб­рис служит основным документом, по которому находят
на мест­ности точки теодолитного хода.

Для
передачи координат на точки теодолитных ходов произво­дят привязку их к
геодезическим пунктам более высокого класса. Привязка состоит в том, что
определяют положение хотя бы одной точки хода относительно точек более высокого
класса: измеряют между ними расстояние и примычный угол. Плановую привязку
называют передачей координат и дирекционных углов с пунктов привязки на точки ходов. В
зависимости от числа пунк­тов государственной геодези­ческой сети и удаленности
их от точек теодолитного хода при­вязку производят разными спо­собами.
Например, пункты го­сударственной геодезической сети II, III включают в теодо­литный ход, измеряют
примычные углы β₁ и β₂ и линии D_II–I, D_III-4 (рис. 2). Результаты линейных и угло­вых измерений обрабатывают.

Схема привязки теодолитного                                                                                 хода к твёрдым пунктам II и III

Первичную обработку (полевой контроль и оценку их пригодности для последующих
вычислений) выполняют непос­редственно в полевых журналах. При первичной
обработке нахо­дят среднее значение из множества измерений одной и той же
величины, определяют допустимость отклонений, делают повтор­ные вычисления
(выполняет другой специалист).

Основную обработку результатов измерений в теодо­литном ходе
выполняют после полевого контроля и записывают на бланках-ведомостях.

Исходные данные для обработки: горизонтальные углы, дли­ны
сторон, дирекционный угол примычной стороны и координа­ты точек государственной
геодезической сети, к которым привя­зывают теодолитный ход.

Последовательность обработки и записи результатов следующая:

1.Подсчитывают сумму измеренных углов  и теорети­ческую сумму углов.

Для замкнутого теодолитного хода сумму углов подсчитывают
как сумму углов многоугольника: β_т = 180°(n-2), где п — число углов.

Для разомкнутого теодолитного хода, т. е. хода,
привязанного к пунктам государственной геодезической сети с двух сторон, не­вязку
вычисляют по формуле: f_βпр= a_кл – a_ил  β_изм, где a_кл , a_ил ^— дирекционные углы сторон, к которым привязан
теодолит­ный ход;  β_изм — сумма измеренных углов на вершинах теодо­литного хода.

3. Определяют допустимость вычисленной угловой невязки по сравнению
с заранее вычисленной: f_βпр =2t где t — прибор­ная точность измерения углов; n — число измеряемых углов.

4.  При f_βпр  f_{β доп}
невязку распределяют поровну на все углы введением поправок. Поправки вычисляют
по формуле v_i= f_βпр/ⁿ и вводят с обратным знаком в значения измеренных углов, полу­чая
исправленные углы.

Как правило, поправки вводят с округлением до десятых до­лей
минуты, если углы измерены с точностью до минут. Если измерения более точные,
то при округлении удерживают один лишний знак по отношению к измеренным углам.
Если невязку нельзя разделить поровну на все углы, то большую поправку вво­дят
в утлы, образованные короткими сторонами.

5. По исходному дирекционному углу, который, например, для
стороны II…III равен 260°52,5′, вычисляют дирекционные
углы (рис.3) остальных сторон теодолитного хода. Вычисления ведут по следующему
правилу: дирекционный угол последующей сто­роны равен дирекционному углу
предыдущей стороны плюс 180° и минус горизонтальный угол, лежащий справа по
ходу: a_ш-4 =a_II–III +180⁰ – β_III-4.

 Если при вы­числении
уменьшаемый угол ока­жется меньше вычитаемого, то к уменьшаемому углу
прибавляют 360°. Если вычисленный дирекционный угол окажется больше 360°, то из
него вычитают 360°.

Если измерены левые углы, то дирекционный угол последующей
стороны вычисляют по формуле a_посл = a_пред + β – 180°.

6. Вычисляют значения румбов r.

7. 
Вычисляют горизонтальные проложения длины линий и запи­сывают их
значения в графу 9. Го­ризонтальные проложения линии вычисляют по формуле d = D — ∆d_h, где D —
измеренная длина стороны; ∆d_h – поправка к измеренной длине за наклон к гори­зонту.                                                     

8. Подсчитывают
длину теодолитного хода D.

9.
Используя таблицы приращений координат, вычисляют ∆х и ∆у по
формулам ∆х = Dcosr, ∆y = Dsinr.

В таблицах
приращений координат помещены произведения си­нусов и косинусов углов от 0 до
90° через 1′ на горизонтальные проложения, кратные 10, 20, …, 90 м. Приращения координат
выбирают из таблиц, сохраняя второй знак после запятой. Вычис­ление приращений
координат можно вести на микрокалькулято­ре, с помощью таблиц натуральных
значений тригонометричес­ких функций и таблиц логарифмов.

10.
Подсчитывают алгебраическую сумму положительных и от­рицательных значений
приращений координат ∆х_пр и ∆у_пр

11.  Из каталогов координат в графы выписывают
коор­динаты х и у исходных пунктов II и III и подсчитывают теорети­ческие суммы
приращений координат: ∆х_т =х_к –х_н =х_II –x_III, ∆х_т =х_к –х_н =х_II –x_III,

12. С
учетом знаков находят абсолютные невязки f_x и f_y хода по осям х и у: f_x=

= ∆х_пр – ∆х_т;  
f_у= ∆у_пр – ∆у_т;.

13.  Определяют абсолютную невязку хода f_D =  и за­писывают в ведомость с погрешностью до сотых долей метра.

14.  Вычисляют относительную линейную невязку f_D / гдеD — сумма длин сторон хода, выражаемая простой
дробью с единицей в числителе. Для ее нахождения сумму длин сторон хода целят
на абсолютную линейную невязку.

Алгебраическая сумма координат по каждой оси должна быть
равна ∆х_т и ∆у_т.

                        Х₄ = Х_Ш
+ ∆Х_Ш-4                       У₄ = У_Ш
+ ∆У_ш-4

                        Х₅ = Х₄
+ ∆Х_4-5                         У₅=У4 + ∆у _4-5

                       …………………                           ……………………

                        Х_II = X₁ + ∆X_I–II                         У_II =У_i+ ∆у_I–II

Последние выражения х_II, у_II являются контролем правильно­сти вычислений.

Сумма углов треугольника:

Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.

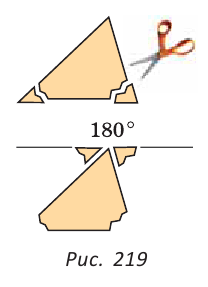
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.

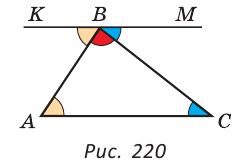
Теорема. Сумма углов треугольника равна 180°.

Дано: АВС (рис. 220).

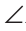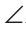Доказать: A+B +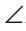C = 180°.

Доказательство:

Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 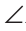KBA =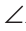A как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей АВ, a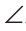MBC =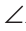C как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей ВС. Так как углы КВА, ABC и МВС образуют развернутый угол, то

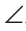KBA +ABC +MBC = 180°. ОтсюдаA +B +C = 180°. Теорема доказана.

Следствия.

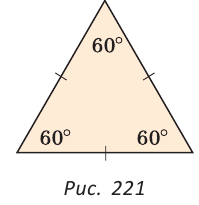
1.    Каждый угол равностороннего треугольника равен 60°. (рис. 221).

2.    Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).

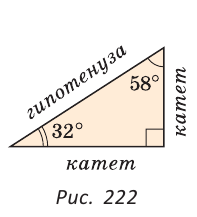
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).    

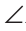Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то1 =2.

Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».

Пример:

В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).

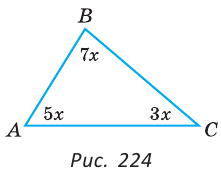
Решение:

Пусть 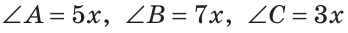 ( 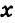— градусная мера одной части).

Так как сумма углов треугольника равна 180°, то

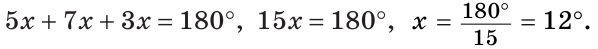
Тогда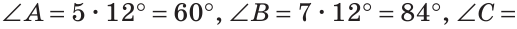  

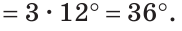
Ответ: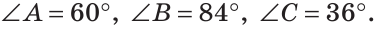

Пример:

В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.

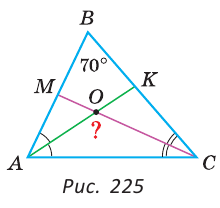
Решение:

Сумма углов А и С треугольника ABC равна 180° – 70° = 110°. Так как биссектриса делит угол пополам, то

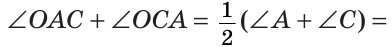
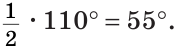
Из треугольника АОС находим: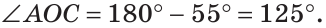

Ответ: 125°.

Замечание. Если 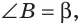 то, рассуждая аналогично, получим формулу: 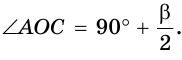Если, например,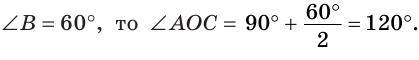

Пример:

Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.

Доказательство:

Пусть СМ — медиана, 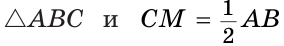 (рис. 226).

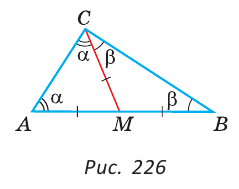
Докажем, чтоACB = 90°. Обозначим A = ,В = . Так как медиана делит сторону пополам, то AM = MB = АВ. Тогда СМ=АМ=МВ. Так как АМС — равнобедренный, тоA =ACM = как углы при основании равнобедренного треугольника. Аналогично, СМВ — равнобедренный и B =BCM = . Сумма углов треугольника ABC, с одной стороны, равна 2 + 2, с другой — равна 180°. Отсюда 2 + 2 = 180°, 2( + ) = 180°, + = 90°. НоACB = + , поэтому

ACB = 90°. 

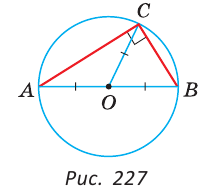
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой». 

Пример:

Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Доказательство:

Пусть в треугольнике ABC (рис. 228) C=90°,A=,B=.

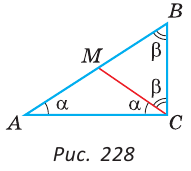
Проведем отрезок СМ так, чтоACM=, и докажем, что СМ — медиана и что СМ=АВ. Угол В дополняет угол А до 90°, aBCM дополняетACM до 90°. Поскольку ACM =A = , тоBCM =. Треугольники АМС и ВМС — равнобедренные по признаку равнобедренного треугольника. Тогда AM = МС и МВ = МС. Отсюда СМ — медиана и СМ = АВ.