VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Полином одной переменной
Полиномы нескольких переменных рассматриваются ☞ ЗДЕСЬ.
Будем обозначать через $ mathbb A_<> $ какое-либо из множеств $ mathbb Z,mathbb Q, mathbb R_<> $ или $ mathbb C_<> $.
Общая информация
Функция вида $$ f(x)=a_0x^n+a_1x^+dots+a_n = sum_^n a_jx^ $$ при $ n_<> in <0,1,dots >$ и $ ,dots,a_n>subset mathbb A $ относительно переменной $ x_<> $ называется полиномом 1) или многочленом от указанной переменной над множеством $ mathbb A_<> $. Число $ a_ $ называется коэффициентом 2) полинома (при $ (n-j)_<> $-й степени переменной), выражение $ a_x^ $ — членом (одночленом) полинома, $ a_ $ — свободным членом, $ x_<>^ $ — мономом.
Пример. Выражения
$$ x^<2>+2,x-679, x^<2>+sqrt<2>x-pi , <mathbf i>, x^<3>— 2,x +sqrt <3>$$ являются полиномами; а $$ x^<-2>+3, x +x^ <2>, x^, sum_^ <infty>x^/j_<> $$ полиномами не являются.
Если $ a_<0>ne 0 $, то член $ a_0x^ $ называется ведущим членом, а $ a_ <0>$ — старшим коэффициентом полинома. При этом число $ n_<> $ называется степенью полинома и обозначается 3) $ deg f_<>(x) $. Полином первой степени называется линейным полиномом. Полином, все коэффициенты которого, кроме, возможно, $ a_ $, равны нулю, называется константой 4) ; будем обозначать его const. Очевидно, что степень константы равна нулю; исключительным для этого утверждения является случай когда константа является нулем. Если все коэффициенты полинома равны нулю, то такой полином называется (тождественно) нулевым. В этом случае его степень не определяется.
На переменную $ x_<> $ мы пока не накладываем ни какого ограничения: она может принимать значения из любого указанного выше множества — не обязательно из того, которому принадлежат коэффициенты полинома. Обозначим область определения полинома через $ mathbb B_<> $.
Значением полинома при (или в точке) $ cin mathbb B_<> $ называется число $$ f(c) = a_0c^n+a_1c^+dots+a_n . $$
Два полинома $$ f(x)=a_0x^n+dots+a_n u g(x)=b_0x^m+dots+b_m $$ с коэффициентами из $ mathbb A $ называются (тождественно) равными: $$ f(x)equiv g(x) $$ если совпадают множества их членов; или, что то же, равны их степени и равны коэффициенты при одинаковых степенях переменной.
Это определение отличается от привычного определения равенства двух функций: две функции $ F_<>(x) $ и $ G(x)_<> $ называются равными на множестве $ mathbb B_<> $ если совпадают их значения при любом $ x in mathbb B_<> $. На самом деле, для случая полиномов эти два определения — алгебраическое и функциональное — эквивалентны.
Теорема. $ f_<>(x)equiv g(x) $ тогда и только тогда, когда $ f(c)=g(c)_<> $ для $ forall cin mathbb B_<> $.
Одним из следствий теоремы является тот факт, что для полинома совершенно не важен порядок следования его членов; в частности, наряду с записью полинома по убывающим степеням переменной, мы имеем право записывать его и по возрастающим: $ f_<>(x)= sum_^n a_x^ $. Форма полинома, в которой его разложение записывается по убывающим степеням переменной, называется его канонической формой. Кроме того, теорема дает нам право на операцию, называемую приведением подобных членов: $$ ax^+bx^j equiv (a+b)x^j, quad ax^jcdot bx^k=ab x^ .$$ Имея в виду этот факт, определим теперь две основные операции для полиномов: сложение и умножение.
Суммой двух полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином, составленный как сумма всех одночленов, входящих в состав $ f_<>(x) $ и $ g_<>(x) $: $$ f(x) + g(x) = (a_n+b_m) + (a_+b_)x+dots + left<begin (a_0+b_0)x^n & npu m=n, \ a_0x^n & npu m n. end right. $$
Теорема. $ deg (f+g_<>)le max (deg f, deg g) $.
Произведением двух полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином, составленный как сумма всевозможных попарных произведений членов первого полинома на члены второго: $$ begin f(x)g(x) &=& a_0b_0x^+(a_1b_0+a_0b_1)x^ +(a_2b_0+a_1b_1+a_0b_2)x^+ \ & &+dots + (a_0b_k+a_1b_+dots+a_kb_0)x^+ dots + a_nb_m . end $$ (В записи коэффициента при $ x^ $ мы полагаем $ a_= 0 $ при $ j>n_<> $ и $ b_ <ell>= 0 $ при $ ell>m_<> $).
Теорема. Если $ f_<>(x) notequiv 0 $ и $ g_<>(x) notequiv 0 $, то $ deg (fcdot g_<>)= deg f + deg g_<> $.
Фактическое выполнение операции перемножения полиномов возможно по схеме, напоминающей алгоритм умножения целых чисел «столбиком»: это позволяет сэкономить время на выписывание степеней переменной.
Пример. Перемножить полиномы
Решение. Представим полиномы наборами их коэффициентов, расположив один из них горизонтально, а второй — вертикально. Умножение полинома $ f_<>(x) $ на $ b_x^ $ сводится к умножению набора $ (a_<0>,dots,a_n) $ на $ b_ $; результат следующего умножения — на $ b_x^ $ — получается аналогичным образом, но записывается со сдвигом на одну позицию вправо. Получившиеся ряды суммируются по столбцам. $$ begin &1 & 0 & 1 & -2& 0 & 3 \ hline 2 & 2 & 0 & 2 & -4 & 0 & 6 \ -3& & -3 & 0 & -3 & 6 & 0 & -9 \ 4 & & & 4 & 0 & 4 & -8 & 0 & 12 \ 0 & & & \ -1 &&&&& -1 & 0 & -1 & 2 & 0 & -3 \ hline& 2 & -3 & 6 & -7 & 9 & -2 & -10 & 14 & 0 & -3 end $$ (В отличие от перемножения чисел здесь результаты сложения в столбиках не переносятся в следующий разряд.)
Ответ. $ 2,x^<9>-3,x^8+6,x^7-7,x^6+9,x^5-2,x^4-10,x^3+14,x^2 — 3 $.
Множество всех полиномов от переменной $ x_<> $ с коэффициентами из $ mathbb A_<> $ будем обозначать $ mathbb A_<> [x] $.
Способы более эффективного умножения полиномов излагаются ☞ ЗДЕСЬ
Схема Хорнера
Задача. Вычислить значение полинома в точке $ c $.
Схема вычисления, заложенная в самом определении, «стóит» $ 3n_<>-1 $ операции: $$ begin & &c^2=ctimes c, & dots, & c^n=c^times c , \ &a_ times c, & a_ times c^2, & dots, & a_0 times c^n ,\ a_n & +a_ times c & + a_ times c^2 & + dots & + a_0 times c^n, end $$ т.е. $ 2n_<>-1 $ операции умножения и $ n_<> $ операций сложения. Организуем теперь вычисления по-другому: $$ begin f(c)&=&a_n+a_c+a_c^2+dots +a_1c^+a_0c^n = \ &=&a_n+cleft(a_+a_c+ dots + a_0c^ right) = \ &= &a_n+cleft(a_+cleft(a_+dots + a_0c^ right) right) = \ &=& dots = \ &=&a_n+cleft(a_+cleft(a_+dots + c(a_1+ a_0c)dots right) right) . end $$ Начинаем вычислять с самой внутренней скобки: $$<mathfrak b>_1= a_1+ a_0c, <mathfrak b>_2= a_2+ <mathfrak b>_1 c,dots, <mathfrak b>_ = a_ +<mathfrak b>_c,, <mathfrak b>_ = a_ +<mathfrak b>_c=f(c) $$ Вычисление каждой величины $ <mathfrak b>_ $ «стоит» $ 2_<> $ операции — одного сложения и одного умножения (при условии, что предварительно вычислено $ <mathfrak b>_^<> $). Приведем компактную запись алгоритма: $$ <mathfrak b>_k = a_k + <mathfrak b>_c quad npu quad <mathfrak b>_0 = a_0 quad u quad kin <1,dots,n > . $$ «Стоимость» вычисления значения $ f_<>(c) $ по этой схеме Хорнера составляет $ 2n_<> $ операций. Налицо экономия по сравнению с прямым способом вычисления $ f_<>(c) $.
Вычисления удобно производить с помощью таблицы, стартовое состояние которой следующее: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 end $$ Будем отсчитывать строки сверху вниз, начиная от горизонтальной черты, т.е. нулевой строкой будем считать строку из коэффициентов полинома. Вычисление значения $ <mathfrak b>_ <1>$ в первой строке производится по схеме: предыдущее число умножается на $ c_<> $ и складывается с верхним, т.е. $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 & underbrace_<<mathfrak b>_1> end $$ Далее вычисления идут по тому же правилу: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 &<mathfrak b>_1&underbrace_1>_<<mathfrak b>_2> end $$ и т.д. Величина, получившаяся в последнем столбце, и будет искомым значением $ f_<>(c) $: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 &<mathfrak b>_1&<mathfrak b>_2&dots &<mathfrak b>_ & <mathfrak b>_& underbrace_>_<<mathfrak b>_n=f(c)> end $$
Пример. Вычислить значение полинома $ x^<5>-3, x +1 $ в точке $ 2+ mathbf i_<> $.
Решение. $$ begin & 1 & 0 & 0 & 0 & -3 & 1 \ hline 2+ mathbf i & 1& 2+mathbf i &3+4 mathbf i &2+11 mathbf i & -10+24mathbf i& -43+38mathbf i end $$
Ответ. $ -43+38mathbf i_<> $.
Выясним теперь смысл коэффициентов $ <mathfrak b>_<1>,dots, <mathfrak b>_ $ первой строки схемы Хорнера.
Теорема. Пусть $ cin mathbb B_<> $ и $ mathbb Bsubset mathbb A_<> $. Полином $ f_<>(x)in mathbb A[x] $ допускает единственное представление в виде:
$$ f(x)equiv (x-c)q(x)+r npu r=constin mathbb A, q(x)in mathbb A[x], deg q = deg f — 1 . $$
Доказательство. Будем искать константу $ r_<> $ и полином $ q_<>(x) $ методом неопределенных коэффициентов: $ q(x)= q_<0>x^+q_1x^+ dots + q_ $. Подставим его в правую часть доказываемого тождества, приведем подобные и приравняем коэффициенты полученного полинома коэффициентам полинома $ f_<>(x) $. Получим линейные уравнения, из которых последовательно определяем $ q_<0>,q_1, dots, q_ $ : $$ begin x^n& a_0&=q_0, & \ x^& a_1&=q_1-q_0c &Rightarrow q_1=a_1+q_0c, \ x^& a_2&=q_2-q_1c &Rightarrow q_2=a_2+q_1c, \ vdots & & dots & \ x & a_&=q_-q_c &Rightarrow q_=a_+q_c,\ 1 & a_n&=qquad -q_c+r & Rightarrow r=a_n+q_c. end $$ Видим, что формулы, определяющие коэффициенты $ q_ $, полностью совпадают с формулами, определяющими элементы первой строки схемы Хорнера, т.е. $ q_0=<mathfrak b>_<0>,dots,q_=<mathfrak b>_ $. Но тогда $ r=a_n+q_c=a_+<mathfrak b>_c=<mathfrak b>_=f(c) $. ♦
Итак, имеем: $$q(x)=<mathfrak b>_0x^+dots+<mathfrak b>_, r=<mathfrak b>_ , $$ при этом все коэффициенты вычисляются по схеме Хорнера, а старший коэффициент полинома $ q_<>(x) $ совпадает со старшим коэффициентом $ f_<>(x) $. Так, для полинома приведенного выше примера имеет место тождество: $$x^5-3, x +1 equiv $$ $$ equiv (x-2-mathbf i)left(x^4+ (2+mathbf i)x^3+(3+4,mathbf i)x^2+ (2+11,mathbf i)x -10+24,mathbf i right) -43+38 mathbf i . $$
Корни
Если значение полинома $ f_<>(x) $ при $ x=cin mathbb B_<> $ равно нулю, то число $ c_<> $ называется корнем полинома $ f_<>(x) $. Иными словами, корень полинома $ f_<>(x) $ — это решение уравнения $ f_<>(x)=0 $, принадлежащее множеству $ mathbb B_<> $.
Уравнение $ f_<>=0 $, в левой части которого стоит полином одной или нескольких переменных, называется алгебраическим.
Задача. Выяснить количество корней полинома $ f_<>(x)in mathbb A[x] $, принадлежащих множеству $ mathbb B_<> $, и вычислить их.
Решить алгебраическое уравнение $ f_<>(x)=0 $ над множеством $ mathbb B $ означает найти все корни $ f_<>(x) $, принадлежащие $ mathbb B_<> $.
На основании теоремы из предыдущего пункта имеет место следующая
Теорема [Безу]. Пусть $ mathbb B subset mathbb A_<> $ и $ cin mathbb B_<> $ — корень полинома $ f_<>(x), deg fge 1 $. Тогда полином $ f_<>(x)in mathbb A [x] $ допускает представление в виде произведения:
$$ f(x)equiv (x-c)f_1(x) , $$ где полином $ f_<1>(x)in mathbb A [x], deg f_1 = deg f — 1 $ определяется единственным образом.
Итак, теорема Безу утверждает, что в случае существования корня полинома, возможно разложение этого полинома в произведение двух полиномов — одного первой степени и одного полинома степени, на единицу меньшей исходного. Тем самым, задача о нахождении корней полинома $ f_<>(x) $ сведется к аналогичной задаче для полинома $ f_<1>(x) $; вторая задача может оказаться более простой за счет понижения степени.
Фактическое нахождение полинома $ f_<1>(x) $ возможно произвести с помощью схемы Хорнера.
Пример. Решить уравнение
$$ x^<3>+3 mathbf i, x^2-3(1+2 mathbf i)x+10-5 mathbf i =0 $$ над множеством $ mathbb C_<> $, если известно, что число $ (-1-2 mathbf i)_<> $ — одно из его решений.
Решение. Строим схему Хорнера: $$ begin & 1& 3mathbf i & -3(1+2 mathbf i) & 10-5 mathbf i \ hline -1-2 mathbf i & 1& -1+ mathbf i & -5 mathbf i & 0 end $$ Видим, что число $ (-1-2 mathbf i)_<> $ действительно является корнем полинома, и, следовательно, последний раскладывается в произведение двух полиномов: линейного и квадратичного. Коэффициенты квадратичного полинома выбираются из той же схемы: $$ (x+1+2 mathbf i )(x^2 + (-1+ mathbf i )x- 5 mathbf i) . $$ Квадратное уравнение над $ mathbb C_<> $ можно решить (см. ☞ ЗДЕСЬ ), его корни: $ (-1-2 mathbf i)_<> $ и $ 2+mathbf i_<> $.
Ответ. $ (-1-2 mathbf i), 2+ mathbf i_<> $.
Если полином $ f_<>(x) $ раскладывается в произведение $ f_<>(x)equiv (x-c)f_1(x) $, то полином $ (x-c) $ называется линейным множителем для $ f_<>(x) $ над множеством $ mathbb B_<> $.
Для того, чтобы $ (x-c)_<> $ был линейным множителем для $ f_<>(x) $ необходимо и достаточно чтобы число $ c_<> $ было корнем $ f_<>(x) $.
Примеры показывают, что не для всякого полинома и множества $ mathbb B_<> $ корни существуют. Очевидно не имеет корней полином нулевой степени (константа, отличная от нуля); любой полином первой степени над $ mathbb A_<> $ имеет единственный корень, принадлежащий $ mathbb A_<> $. Квадратный полином $ x^<2>+1 $ не имеет вещественных корней, но имеет мнимые.
Основная теорема высшей алгебры
Теорема. Любой полином с комплексными коэффициентами, степень которого больше нуля, имеет хотя бы один корень, в общем случае, комплексный.
Эта теорема гарантирует существование корня $ lambda_<1>in mathbb C $. На основании теоремы Безу, можно утверждать, что $ f_<>(x) $ допускает представление $$ f(x)equiv (x-lambda_1)f_1(x) quad npu quad f_1(x)in mathbb C [x], deg f_1(x)=deg f(x) -1 .$$ Если $ deg f_<1>(x) ge 1 $, то, по той же теореме, полином $ f_<1>(x) $ также должен обладать корнем, который мы обозначим 5) $ lambda_ <2>$; теорема Безу гарантирует тогда представление $$ f(x)equiv (x-lambda_1)(x-lambda_2)f_2(x) quad npu quad f_2(x)in mathbb C [x], deg f_2(x)=deg f(x) -2 .$$ Продолжая процесс далее, мы за $ n_<> $ шагов придем к представлению $$ f(x)equiv (x-lambda_1)(x-lambda_2)times dots times (x-lambda_n)f_n(x) quad npu quad f_n(x)in mathbb C[x], deg f_n(x)=0 ,$$ т.е. полином $ f_(x)^<> $ представляет собой константу. На основании условия тождественного равенства полиномов утверждаем, что $ f_(x) equiv a_0 $. Таким образом приходим к следующей альтернативной версии основной теоремы высшей алгебры.
Теорема. Для произвольного полинома $ f_<>(x) $ степени $ n_<>ge 1 $ существует его представление в виде произведения линейных множителей
$$ f(x)equiv a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_n) ; $$ это представление единственно с точностью до перестановки сомножителей.
Как уже отмечалось в доказательстве теоремы, в этом представлении могут встречаться одинаковые линейные сомножители. Собрав их вместе, получим иной вид этого представления $$ f(x)equiv a_0(x-lambda_1)^<<mathfrak m>_<1>>times dots times (x-lambda_<mathfrak r>)^<<mathfrak m>_<<mathfrak r>>> , npu <mathfrak m>_<1>+<mathfrak m>_<2>+dots+<mathfrak m>_<mathfrak r>=n $$ и все числа $ lambda_<1>,dots,lambda_ <mathfrak r>$ теперь различны. Эта формула называется формулой разложения полинома $ f_<>(x) $ на линейные сомножители или линейным представлением полинома $ f_<>(x) $; при этом число $ <mathfrak m>_^<>in mathbb N $ называется кратностью линейного сомножителя $ x-lambda_ $ или кратностью корня $ lambda_ $ в полиноме $ f_<>(x) $. Корень $ lambda_ $ называется простым, если $ <mathfrak m>_=1_<> $ и кратным кратности $ <mathfrak m>_^<> $ если $ <mathfrak m>_>1_<> $ (двойным или двукратным, если $ <mathfrak m>_=2_<> $, тройным или трехкратным если $ <mathfrak m>_=3_<> $ и т.д.)
Пример. Найти линейное представление полинома $ f(x)=x^<6>-2, x^3+1 $.
Решение. Линейное представление легко получить если сначала заметить, что $ f(x)equiv (x^3-1)^ <2>$, а затем использовать выражения для корней кубических из единицы: $$f(x)equiv (x-1)^2 left(x- frac<-1+ mathbf i sqrt<3>> <2>right)^2 left(x- frac<-1 – mathbf i sqrt<3>> <2>right)^2 . $$ Все корни полинома имеют вторую кратность. ♦
Выведение условия наличия кратного корня (в терминах коэффициентов полинома) ☞ ЗДЕСЬ. При известном корне, нахождение его кратности ☞ ЗДЕСЬ.
Теорема. Два полинома, степени которых не превосходят $ n_<> $, равны тождественно если они имеют равные значения более чем при $ n_<> $ различных значениях переменной.
Доказательство необходимости очевидно. Если полиномы $ f_<>(x) $ и $ g_<>(x) $ удовлетворяют условию теоремы, то полином $ f(x)-g_<>(x) $ должен иметь более, чем $ n_<> $ корней, что, ввиду основной теоремы высшей алгебры, возможно лишь если он тождественно нулевой. ♦
Теорема утверждает, что полином $ f_<>(x) $ степени, $ le n_<> $, однозначно определяется своими значениями при более чем $ n_<> $ различных значениях переменной. Можно ли эти значения задавать произвольно? Оказывается задание $ (n+1)_<> $-й пары $ (x_<1>,y_1),dots,(x_,y_) $ при всех различных $ x_<1>,dots,x_ $ позволяет однозначно определить полином $ f_<>(x) $ такой, что $ f(x_<1>)=y_1,dots,f(x_)=y_ $ и $ deg f_<> le n $. Практические способы решения этой задачи обсуждаются в разделе ☟
Интерполяция
Корни и коэффициенты полинома
Симметрические функции корней
Разложение полинома $ f_<>(x) $ на линейные множители дает интересные соотношения между корнями полинома и его коэффициентами. Сначала выведем их для малых степеней. Для $ n_<>=2 $: $$a_0x^2+a_1x+a_2equiv a_0(x-lambda_1)(x-lambda_2)equiv a_0x^2-a_0(lambda_1+lambda_2)x+a_0lambda_1lambda_2 Rightarrow $$ $$ Rightarrow left< begin lambda_1+lambda_2&=&-a_1/a_0, \ lambda_1lambda_2&=&a_2/a_0, end right. $$ т.е. получили формулы известные из школьного курса алгебры. Далее, для $ n_<>=3 $: $$a_0x^3+a_1x^2+a_2x+a_3equiv a_0(x-lambda_1)(x-lambda_2)(x-lambda_3)equiv $$ $$equiv a_0x^3-a_0(lambda_1+lambda_2+lambda_3)x^2+a_0(lambda_1lambda_2 + lambda_1lambda_3+lambda_2lambda_3)x-a_0lambda_1lambda_2lambda_3 Rightarrow $$ $$ Rightarrow left< begin lambda_1+lambda_2+lambda_3&=&-a_1/a_0, \ lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3&=&a_2/a_0,\ lambda_1lambda_2lambda_3&=&-a_3/a_0. end right. $$
Теорема. Для корней $ lambda_<1>,dots,lambda_n $ полинома
$$ f(x)=a_<0>x^n+a_1x^+dots+a_n,, a_0ne 0 $$ справедливы формулы Виета $$ sum_ <1 le jle n>lambda_j = lambda_1+ dots+ lambda_n= -frac, $$ $$ sum_<1le j_1 ☞ ЗДЕСЬ.
Биографические заметки о Виете ☞ ЗДЕСЬ
Пример. Найти все корни полинома $ 3,x^3-16,x^2+23,x-6 $, если известно, что произведение двух из них равно $ 1_<> $.
Решение. Имеем: $$ left< begin lambda_1+lambda_2+lambda_3&=&16/3, \ lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3 &=&23/3,\ lambda_1lambda_2lambda_3&=&6/3=2. end right. $$ Вдобавок к этим уравнениям, мы должны записать дополнительное условие: $$lambda_1 lambda_2=1 .$$ Из третьего уравнения системы получаем тогда $ lambda_3=2 $. Подставив его в два оставшихся, придем к двум идентичным: $$lambda_1 + lambda_2=10/3 .$$ Теперь для нахождения неизвестных $ lambda_ <1>$ и $ lambda_ <2>$ можем воспользоваться формулами Виета «в обратном порядке», составив квадратный полином, имеющий их корнями: $$t^2-10/3,t+1 .$$
Ответ. $ 2,,3,, 1/3 $.
Можно ли использовать формулы Виета для решения уравнения ?
Ответ ☞ ЗДЕСЬ.
Обдумаем еще раз результаты основной теоремы высшей алгебры и формул Виета. С одной стороны, задав коэффициенты $ a_<0>,a_1,dots,a_n $ мы однозначно определяем набор из $ n_<> $ комплексных чисел $ lambda_<1>,dots,lambda_n $ — корней этого полинома. С другой стороны, задав произвольным образом набор корней $ lambda_<1>,dots,lambda_n $, по формулам Виета однозначно определим величины $ a_1/a_0,dots,a_n/a_0 $. Для простоты, рассмотрим подмножество полиномов степени $ n_<> $, имеющих старший коэффициент равным $ 1_<> $. Получаем тогда взаимно-однозначное соответствие: $$ (a_1,dots,a_n) leftrightarrow (lambda_1,dots,lambda_n) . $$ Итак, каждый корень $ lambda_ $ полинома является какой-то функцией его коэффициентов $ a_1,dots,a_ $, т.е. формально говоря, функцией от многих переменных. Относительно этой функции мы пока ничего сказать не можем; более того, как мы узнаем НИЖЕ, для степеней полинома бóльших $ 4_<> $ не существует «хороших» общих формул, выражающих корни полинома через его коэффициенты. Несмотря на это, формулы Виета подтверждают, что некоторые комбинации этих неизвестных нам функций оказываются равными коэффициентам полинома. Какова основная отличительная особенность этих комбинаций?
Функция $ Phi(x_1,dots,x_n) $ называется симметрической функцией своих переменных, если ее значение не меняется ни при какой перестановке этих переменных: $$Phi(x_1,dots,x_n) equiv Phi(x_,dots,x_) $$ при всех различных $ j_1,dots, j_n in <1,dots,n>$.
Пример. Функции
$$ sqrt <1+x_1x_2x_3>, frac+frac+frac $$ являются симметрическими функциями переменных $ x_1,x_2,x_3 $, а функция $$ x_1^2x_2x_3+x_1x_2^2x_3 $$ симметрической функцией не является, поскольку ее значения меняются при перестанове $ (x_1,x_2,x_3) leftrightarrow (x_3,x_2,x_1) $.
В левых частях формул Виета как раз и стоят симметрические полиномы относительно $ lambda_<1>,dots,lambda_n $. Оказывается результат теоремы допускает следующее обобщение.
Теорема [Гаусс]. Значение любого симметрического полинома $ Phi(x_1,dots,x_n) $ на корнях $ lambda_1,dots,lambda_n $ полинома $ x^n+a_1x^+ dots+a_n $ является полиномиальной функцией от $ a_<1>,dots,a_n $: $$ Phi(lambda_1,dots,lambda_n) equiv <mathfrak F>(a_1,dots,a_n) . $$
Пример. Пусть $ lambda_ <1>$ и $ lambda_ <2>$ означают корни полинома $ x^2+a_1x+a_2 $. Выразить
$$lambda_1^2+lambda_2^2-3,lambda_1^2lambda_2-3,lambda_1lambda_2^2$$ через коэффициенты полинома.
Решение. Поскольку выражения для корней квадратного уравнения нам известны: $$ lambda_1= frac<-a_1+sqrt> <2>quad u quad lambda_2= frac<-a_1-sqrt> <2> , $$ то непосредственной подстановкой их в заданный полином, получаем $$ a_1^2-2,a_2+3,a_1a_2 . $$ ♦
Пример. Пусть $ lambda_1,, lambda_2,, lambda_3 $ означают корни полинома $ x^3+a_1x^2+a_2x+a_3 $. Выразить
$$lambda_1^2lambda_2+lambda_1^2lambda_3+lambda_1lambda_2^2+ lambda_1lambda_3^2+lambda_2^2lambda_3+lambda_2lambda_3^2 -lambda_1^2-lambda_2^2-lambda_3^2 $$ через коэффициенты полинома.
Решение. Выделим в требуемом выражении комбинации корней, стоящие в левых частях формул Виета. Первые $ 6_<> $ слагаемых можно представить в виде $$(lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3) (lambda_1+lambda_2+lambda_3)-3lambda_1lambda_2lambda_3 , $$ а $$lambda_1^2+lambda_2^2+lambda_3^2= left(lambda_1+lambda_2+lambda_3 right)^2-2, (lambda_1lambda_2+ lambda_1lambda_3+lambda_2lambda_3) .$$ Далее применяем формулы Виета.
Ответ. $ 3,a_3-a_1a_2-a_1^2+2, a_2 $.
Существуют общие алгоритмы нахождения полинома $ <mathfrak F>$ по заданному полиному $ Phi $: см. [3], [4]. Однако в своей практике я встречал необходимость в подобном представлении лишь для некоторых классов полиномов $ Phi_<> $; сейчас их и рассмотрим.
Суммы Ньютона
Для полинома $ f(x)=a_<0>x^n+a_1x^+dots+a_n, (a_0ne 0) $ его $ k_<> $-й суммой Ньютона называется сумма $ k_<> $-х степеней его корней: $$ s_k=lambda_1^k + dots + lambda_n^k . $$ При этом обычно считают $ k_<> in <mathbb N>$ (хотя формально можно определить суммы Ньютона и для отрицательных индексов $ k_<> $ при условии $ a_ ne 0 $). Для однообразия полагают также $ s_<0>=n $.
Теорема. Суммы Ньютона выражаются рационально через коэффициенты полинома $ f_<>(x) $ посредством следующих рекуррентных формул Ньютона:
Пример.
$$ s_2=(a_1^2-2, a_0a_2) big/ a_0^2 , $$ $$ s_3=-(a_1s_2+a_2s_1+3,a_3)big/ a_0= $$ $$ =-left(a_1 (a_1^2-2, a_0a_2) big/ a_0^2 +a_2 (-a_1 big/ a_0)+3,a_3 right) big/ a_0= $$ $$ =left(-a_1^3+3,a_0a_1a_2-3,a_0^2a_3 right) big/ a_0^3 . $$ ♦
Подробнее о суммах Ньютона ☞ ЗДЕСЬ.
Результант и дискриминант
Пусть $ g(x)=b_0x^m+dots + b_ $ — произвольный полином из $ mathbb A_<> [x] $. Тогда выражение $$ g(lambda_1) times dots times g(lambda_n) $$ является симметрическим полиномом от корней $ lambda_<1>,dots,lambda_n $ полинома $ f_<>(x) $. По теореме Гаусса, оно должно рационально выражаться через коэффициенты $ a_<0>,dots,a_n $. С другой стороны, очевидно, это выражение обращается в нуль тогда и только тогда, когда хотя бы один сомножитель обратится в нуль, т.е. будет существовать общий корень полиномов $ f_<>(x) $ и $ g_<>(x) $. Выражение $$ a_0^m prod_^n g(lambda_j) $$ называется результантом полиномов $ f_<>(x) $ и $ g_<>(x) $.
Способы вычисления результанта, его свойства и применения ☞ ЗДЕСЬ.
В частном случае, когда $ g_<>(x) $ совпадает с производной полинома $ f_<>(x) $ результант переходит в дискриминант — выражение отличающееся от $$ a_0^ prod_^n f^<prime>(lambda_j) $$ только сомножителем $ (-1)^/a_0 $ и обращающееся в нуль тогда и только тогда, когда $ f^<prime>(x) $ имеет общий корень с $ f_<>(x) $. Как мы увидим НИЖЕ, последнее условие оказывается необходимым и достаточным наличия у полинома $ f_<>(x) $ кратного корня.
Пример. Для $ f(x)=a_<0>x^2+a_1x+a_2 $ указанное произведение оказывается равным
$$ (2a_0lambda_1 +a_1)(2a_0lambda_2 +a_1)=(4a_0^2lambda_1 lambda_2+2a_0a_1(lambda_1 +lambda_2)+a_1^2)= $$ $$ =left(4a_0^2 frac-2a_0a_1frac+a_1^2right)=4a_0a_2-a_1^2, $$ т.е. привычному «школьному» понятию.
Способы вычисления дискриминанта, его свойства и применения ☞ ЗДЕСЬ.
Преобразования корней
Если $ lambda_<1>,dots,lambda_n $ — корни полинома $ f(x)=a_0x^n+a_1x^+dots+a_ $, то
1. корнями полинома $$ f(-x)=(-1)^nleft(a_0x^n-a_1x^+dots+(-1)^na_nright) = $$ $$ =(-1)^n sum_^n (-1)^ja_jx^ $$ являются $ -lambda_1, dots, -lambda_n $;
2. корнями полинома $$f(x- <coloralpha >)=a_0(x- <coloralpha > )^n+a_1(x- <coloralpha >)^+dots+a_n= $$ $$ = sum_^n a_j(x- <coloralpha >)^ $$ являются $ <coloralpha >+lambda_1, dots, <coloralpha >+lambda_n $;
3. при дополнительном условии, что $ a_ ne 0 $, корнями полинома $$f^<ast>(x)= x^nfleft(1/x right) equiv a_0+a_1x+dots+a_nx^n = $$ $$ =sum_^n a_jx^ $$ являются $ 1/<lambda_1>, dots, 1/ <lambda_n>$.
Преобразования 1-3 часто используются как при выводе теоретических результатов так и в практике вычислений.
Поясним идею этих применений. Корни исходного и корни преобразованного полинома остаются неизвестными. Допустим, мы получили какой-то результат, касающийся оценки положительных корней полинома $ f_<>(x) in mathbb R[x] $, и хотим распространить эту оценку и на отрицательные корни (см., к примеру, ☟ НИЖЕ ). Производится замена переменной $ x rightarrow — x $, которая меняет знаки всех корней: отрицательные становятся положительными, и к новому полиному применяется полученный результат. В приложениях возникают и более сложные преобразования корней: когда, к примеру, все их надо «загнать» в ограниченную область комплексной плоскости — скажем, в круг $ |x|le 1 $ (см. ☟ НИЖЕ ).
Пример. Построить полином $ F_<>(x) $, корни которого равны квадратам корней полинома $ f_<>(x) $.
Непрерывность корней
Теорема [5]. Корни полинома
$$ f(x)=x^n+a_1x^+dots+a_n in mathbb C[x],quad nge 1 $$ являются непрерывными функциями его коэффициентов. Строго говоря, если $ lambda_1,dots,lambda_ $ — корни этого полинома, а $ <tilde lambda_1>,dots, <tilde lambda_n>$ — корни полинома $$<tilde f>(x)=x^n+<tilde a>_1x^+dots+<tilde a>_n in mathbb C[x] , $$ то эти корни можно перенумеровать таким образом, чтобы $$ |lambda_j-<tilde lambda>_j| | | | | | . При увеличении значений $ <coloralpha >_<> $ от $ -2 $ до $ -1_<> $ происходит «дрейф» корней — плавный, но разный по скорости. К примеру, синий и фиолетовый корни меняются очень медленно, а вот зеленый и малиновый быстро сближаются пока не столкнутся при значении $ <coloralpha >=-1 $: $$ lambda_1approx -1.5096-0.4133 <mathbf i>, lambda_2 approx -0.6768+0.1479 <mathbf i>, lambda_3 approx 0.4364-0.4845 <mathbf i>, lambda_4 = 1+ <mathbf i>, $$ $$ lambda_5 =1+ <mathbf i> . $$ Что происходит при дальнейшем увеличении $ <coloralpha >_<> $? Число корней должно остаться инвариантным — по основной теореме высшей алгебры оно продолжает совпадать со степенью полинома, т.е. корни не аннигилируют. Поэтому столкнувшиеся корни порождают два новых — голубой и коричневый — которые начинают расходиться. При $ <coloralpha >=1 $ ситуация следующая: $$ lambda_1 approx -2.3350+0.4836 <mathbf i>, lambda_2 approx -0.5794+0.1185<mathbf i>, lambda_3 approx 0.2721-0.4926 <mathbf i>, $$ $$ lambda_4 approx -0.3888+2.5945 <mathbf i>, lambda_5 approx 0.5832+0.3480 <mathbf i>. $$ Имея перед глазами полную картину истории, понимаем, что корни, обозначенные $ lambda_ <1>$ (красный) и $ lambda_ <4>$ (голубой), стремятся к столкновению — и оно действительно происходит при $ <coloralpha >=2 $: $$ lambda_1 = -2+2<mathbf i>, lambda_2 approx -0.5458+0.1142 <mathbf i>, lambda_3 approx 0.2296-0.4712 <mathbf i>, lambda_4 = -2+2<mathbf i>, $$ $$ lambda_5 approx 0.5193+0.3101 <mathbf i>. $$ Дальнейшую динамику можем предсказать «по прецеденту» — столкнувшиеся корни должны разойтись. При $ <coloralpha >=3_<> $: $$ lambda_1 approx -4.0682+3.6140 <mathbf i>, lambda_2 approx -0.5184+0.1116 <mathbf i>, lambda_3 approx 0.2007-0.4506<mathbf i>, $$ $$ lambda_4 approx -1.2359+1.2927<mathbf i>, lambda_5 approx 0.4759+0.2864 <mathbf i>. $$ ♦
К какому числу стремится желтый корень при $ <coloralpha > to +infty $ ?
Последний пример наводит на еще одну гипотезу: мы видим, что графики корней получились гладкими, за исключением, возможно, некоторых специфических точек.
Теорема. Корни полинома
$$ f(x)=x^n+a_1x^+dots+a_n in mathbb C[x] $$ являются непрерывно дифференцируемыми функциями коэффициентов за исключением тех наборов значений коэффициентов, которые определяют кратные корни.
Доказательство ☞ ЗДЕСЬ.
Условие наличия кратного корня у полинома $ f_<>(x) $ может быть получено в виде явного условия на его коэффициенты. См. ☞ ДИСКРИМИНАНТ.
Поиск корней алгебраических уравнений: решение в радикалах
Можно ли выразить корни полинома $ f(x)in mathbb C[x] $ в виде «хороших» функций от его коэффициентов? Вспомним, что для квадратного уравнения существует общая формула вычисления корней: $$x^2+ax+b=0 Rightarrow lambda_<1,2>=frac<-apm sqrt> <2> . $$ Эта формула включает в себя элементарные алгебраические операции $ +,- ,times, div $ и операцию извлечения квадратного корня. По аналогии можно сформулировать и общую задачу.
Задача. Найти выражения корней полинома степени $ n_<>>2 $ в виде функций его коэффициентов; при этом функции должны представлять конечную комбинацию элементарных алгебраических операций и операций извлечения корней произвольных (целых) степеней.
Поставленная задача называется задачей о разрешимости уравнения в радикалах 6) .
Оказывается, что любое уравнение третьей или четвертой степени разрешимо в радикалах. Перед тем, как изложить способы их решения, сделаем два упрощения. Первое из них заключается в том, что уравнение $ f_<>(x)=0 $ делится на старший коэффициент полинома $ f_<>(x) $.
Полином называется нормализованным 7) , если его старший коэффициент равен $ 1_<> $. Операция деления полинома на его старший коэффициент называется нормализацией полинома.
Очевидно, что нормализованный полином имеет те же корни, и в тех же кратностях, что и исходный. Для простоты обозначений, будем считать, что полином уже нормализован: $$ f(x)=x^n+a_1x^+dots+a_n .$$
Второе упрощение заключается в замене переменной (подстановке): $ x=y+ <coloralpha > $. Ее результатом будет новый полином той же степени, что и исходный, относительно переменной $ y_<> $: $$ F(y)equiv f(y+ <coloralpha >) , . $$ Корни нового полинома связаны (cм. преобразование 2 ☞ ЗДЕСЬ ) с корнями старого по формуле $ lambda_j = Lambda_j+ <coloralpha > $; так что, найдя корни одного полинома, легко установим и корни другого. Подберем теперь параметр $ <coloralpha > $ так, чтобы обратить в нуль коэффициент при $ y^ $ в полиноме $ F_<>(y) $. Используя формулу бинома Ньютона, получаем $$ begin f(x)&=&x^n+a_1x^+a_2x^+dots+a_n= \ &=&(y+ <coloralpha >)^n +a_1(y+ <coloralpha >)^+a_2(y+ <coloralpha >)^+dots+a_n = \ &=&y^n + C_n^1 <coloralpha > y^ +C_n^2 <coloralpha >^2 y^+dots+ <coloralpha >^n + \ & & qquad + a_1y^+a_1 C_^1 <coloralpha > y^+dots +a_1 <coloralpha >^ + \ & & quad qquad qquad +a_2y^ + dots + a_n. end $$ Понятно, что если положить $ <coloralpha >= — a_1/n $, то коэффициент при $ y^ $ исчезнет. Для простоты обозначений, будем считать, что полином уже предварительно подвергнут такому преобразованию: $$ f(x)=x^n qquad +a_2x^+dots+a_n .$$
Уравнение третьей степени
Рассмотрим уравнение третьей степени: $$ x^3+p,x+q=0 $$ Сделаем в этом уравнении замену переменной: $ x=u+v $, введя две неизвестные $ u_<> $ и $ v_<> $; получим: $$ u^3+v^3+3,uv(u+v)+p(u+v)+q=0 . $$ Сгруппируем: $$ u^3+v^3+(3,uv+p)(u+v)+q=0 . $$ Подчиним теперь неизвестные $ u_<> $ и $ v_<> $ условию $$ 3,uv+p=0 iff uv=-frac
<3> . $$ Тогда предыдущее уравнение приведется к виду $$u^3+v^3=-q . $$ Итак, для определения неизвестных величин $ u_<> $ и $ v_<> $ мы получили систему уравнений $$ u^3+v^3=-q, uv=-frac
<3>. $$ Возведя последнее уравнение в куб, получим $$ u^3v^3=-frac <27> . $$ Два полученных равенства, связывающие $ u^3 $ и $ v^3 $, позволяет утверждать, что эти величины являются решениями квадратного уравнения: $$t^2+q,t- frac<27>=0 .$$
Выражение $$ Delta = frac<4>+frac <27>$$ называется дискриминантом кубического уравнения.
Решив квадратное уравнение, получим: $$ u^3=-frac<2>+ sqrt<Delta>, v^3=-frac
<2>— sqrt <Delta> . $$ В итоге имеем формулу для решений уравнения: $$ x=u+v=sqrt[3]<-frac
<2>+sqrt<frac<4>+frac<27>>>+ sqrt[3]<-frac
<2>-sqrt<frac<4>+frac<27>>> ; $$ она называется формулой Кардано.
Формула Кардано не очень удобна для практических вычислений. Вспомним, что корень кубический из комплексного числа может принимать три различных значения. Решение же, представленное формулой Кардано, имеет в правой части комбинацию из двух кубических корней. Таким образом, получаем 9 всевозможных комбинаций из значений корней кубических. С другой стороны, основная теорема высшей алгебры утверждает, что кубическое уравнение должно иметь только три решения. Для того, чтобы установить соответствие между значениями $ u_<> $ и $ v_<> $, обратимся к условию $ uv=-p/3 $ . Согласно этому условию, задание значений для $ u_<> $ позволит однозначно восстановить $ v_<> $. Пусть $$ u_1=sqrt[3]<-frac<2>+sqrt<frac<4>+frac<27>>> $$ какое-то одно из трех возможных значений корня кубического. Два оставшихся значения корня кубического получаются домножением $ u_1 $ на корни кубические из единицы: $$u_2=u_1varepsilon_1, u_3=u_1varepsilon_2 $$ при $$varepsilon_1=cos frac<2pi> <3>+ <mathbf i>sin frac<2pi><3>= frac<-1><2>+ <mathbf i>frac<sqrt<3>> <2> u varepsilon_2=cos frac<4pi> <3>+ <mathbf i>sin frac<4pi><3>= frac<-1><2>— <mathbf i>frac< sqrt<3>> < 2> . $$ Если теперь взять $$ v_1=-frac
<3u_1> , $$ то решения кубического уравнения можно выразить в виде комбинаций $ u_1 $ и $ v_1 $: $$ begin lambda_1&=&u_1+v_1, \ lambda_2&=&u_2+v_2=u_2-frac<displaystyle p><displaystyle 3u_2>=u_1varepsilon_1-frac<displaystyle p> <displaystyle 3u_1varepsilon_1>=u_1varepsilon_1-frac<displaystyle pvarepsilon_2><displaystyle 3u_1>=u_1varepsilon_1+v_1varepsilon_2,\ lambda_3&=&u_3+v_3=u_1varepsilon_2+v_1varepsilon_1 . end $$ Окончательно получаем формулы для вычисления корней: $$ left< begin lambda_1&=&u_1+v_1, \ lambda_2&=&-frac<scriptstyle 1><scriptstyle 2>(u_1+v_1) + <mathbf i>frac<scriptstyle sqrt<3>> <scriptstyle 2>(u_1-v_1),\ lambda_3&=&-frac<scriptstyle 1><scriptstyle 2>(u_1+v_1) — <mathbf i>frac<scriptstyle sqrt<3>> <scriptstyle 2>(u_1-v_1), end right. $$ где $ u_1 $ — одно из значений корня кубического, а $ v_1 $ связано с ним соотношением $ v_1=-p/(3u_1) $.
Пример [2]. Решить уравнение $ x^3-6<mathbf i>,x^2-10,x+8 <mathbf i>=0 $.
Решение. Подстановка $ x=y+2 <mathbf i>$ приводит уравнение к виду $$y^3+2,y+4 <mathbf i>=0 , $$ т.е. $ p=2,,q=4 <mathbf i>$. Далее $$Delta=-frac<100> <27> Rightarrow sqrt <Delta>= pm frac<10 <mathbf i>><3sqrt<3>> Rightarrow u_1=sqrt[3]<left(-2 + frac<10><3sqrt<3>> right)<mathbf i>> . $$ Одно из значений последнего корня: $$u_1=-<mathbf i>, sqrt[3]<-2 + frac<10><3sqrt<3>>> , $$ это выражение можно упростить, если повезет заметить, что подкоренное выражение равно $ left(-1+1/<sqrt<3>>right)^3 $: $$u_1=<mathbf i>left(1-frac<1><sqrt<3>>right) Rightarrow v_1=-frac
<3u_1>= <mathbf i>left(1+frac<1><sqrt<3>>right) . $$ Получаем: $$mu_1=2, <mathbf i>, mu_2=1- <mathbf i>, mu_3=-1- <mathbf i> .$$ Значения корней исходного уравнения получатся «сдвигом» на $ 2 <mathbf i>$.
Дальнейший анализ формулы Кардано ☞ ЗДЕСЬ
Уравнение четвертой степени
$ x^4+a_1x^3+a_2x^2+a_3x+a_4 = 0 $ также может быть решено в радикалах. Идея решения заключается в сведении задачи к решению некоторого кубического уравнения. Ее реализация ☞ ЗДЕСЬ.
Уравнения высших степеней
Успех в решении уравнений третьей и четвертой степени побудил исследователей искать подобные формулы для уравнений высших степеней. Методология подхода была очевидна: свести решение уравнения $ n $-й степени к решению уравнения $ (n-1) $-й степени. Однако, несмотря на почти трехвековые усилия лучших математиков, решить уравнение пятой степени не удавалось. Наконец, в начале XIX века был получен отрицательный результат.
Теорема [Руффини, Абель]. Уравнение степени выше четвертой в общем случае неразрешимо в радикалах.
Пример. Уравнение $ x^5-4, x -2=0 $ не разрешимо в радикалах.
Установить разрешимо или нет данное конкретное уравнение в радикалах возможно с помощью теории, развитой французским математиком Галуа.
Пример. Уравнение $ x^5+x+1=0 $ разрешимо в радикалах, поскольку
Отрицательный характер результата теоремы Руффини-Абеля не должен слишком уж разочаровывать. Он означает только лишь то, что корни полинома нельзя представить в виде формулы, состоящей из конечного набора сравнительно простых функций. Тем не менее, если расширить класс допустимых в формуле функций (или допустить бесконечность числа операций), представление для корня можно найти (см., к примеру, ☞ ЗДЕСЬ ). Наконец, для практических задач часто более важна не столько «красивая» аналитическая формула для корня, сколько приближенное его значение с требуемой точностью.
Поиск корней алгебраических уравнений: возможность упрощений
Для некоторых классов уравнений удается упростить задачу: свести решение исходного уравнения к решению уравнения меньшей степени 8) .
Возвратное уравнение
Так называется уравнение вида $ a_0z^n+a_1z^+dots+a_z+a_n=0, a_0ne 0 $, у которого набор коэффициентов $ (a_0,a_1,dots, a_,a_n) $ симметричен относительно середины: $$ a_0=a_,a_1=a_,dots, a_=a_ dots $$
Пример. Уравнения
$$ z^2-3,z+1=0,quad -sqrt<2>z^5+2,z^4+mathbf i z^3+2,z-sqrt<2>,quad z^n+1=0 , $$ $$ z^n+z^+z^+dots + z^2 +z+1=0 $$ являются возвратными.
Методы упрощения подобных уравнений ☞ ЗДЕСЬ.
Делимость полиномов
Здесь $ mathbb A_<> $ означает какое-то из множеств $ mathbb Q, mathbb R $ или $ mathbb C_<> $.
Теорема. Для полиномов $ f_<>(x) $ и $ g(x)not equiv 0 $ из $ mathbb A[x] $ существует единственная пара полиномов $ q_<>(x) $ и $ r_<>(x) $ из $ mathbb A[x] $ таких, что
$$ f(x) equiv g(x) q(x) + r(x) quad mbox < и >quad deg r ☞ ЗДЕСЬ.
В этом представлении полином $ f_<>(x) $ называется делимым, $ g_<>(x) $ — делителем, $ r_<>(x) $ — остатком от деления $ f_<>(x) $ на $ g_<>(x) $, а $ q_<>(x) $ — частным 9) . При $ r(x) equiv 0 $, говорят, что полином $ f_<>(x) $ делится (нацело) на $ g_<>(x) $, а полином $ g_<>(x) $ называется делителем $ f_<>(x) $. Тривиальными делителями полинома $ f_<>(x) $ называют сам полином $ f_<>(x) $ и полином тождественно равный $ 1_<> $ (оба — с точностью до домножения на ненулевую константу). Любой другой делитель полинома (если существует) называется нетривиальным.
Пример [1]. Найти частное и остаток от деления
$$f(x)=2, x^5 +x^4 -x^2 +2, x +1 quad mbox < на >quad g(x)=x^3+2, x^2 — x -1 .$$
Ответ. $ q(x)=2, x^2 -3, x + 8, r(x)=-18, x^2 + 7, x +9 $.
Фактическое выполнение операции деления полиномов можно производить, действуя лишь над наборами их коэффициентов — подобно тому, как мы производили их умножение.
Пример. Найти частное и остаток от деления
$$f(x)=x^8+x^7+3,x^4-1 quad mbox < на >quad g(x)=x^4-3, x^3 +4, x +1 .$$
Решение. $$ begin 1& 1 &0&0&3&0 &0 & 0&-1 &&1 -3 0 4 1\ 1&-3 &0&4&1& & & & && overline < 1 4 12 32 82>\ hline &4 & 0 &-4 & 2 & 0 & <> \ &4 &-12& 0 & 16 & 4& <> \ hline && 12& -4 &-14 & -4 & 0 & <> \ && 12& -36 & 0 & 48 & 12 & <> \ hline &&& 32 & -14& -52&-12 & 0 & <> \ &&& 32 & -96& 0 & 128& 32 & <> \ hline &&&&82&-52&-140&-32&-1 \ &&&&82&-246&0&328&82 \ hline &&&&&194&-140&-360&-83 end $$
Ответ. $ q(x)=x^4+4,x^3+12,x^2+32, x+82,, r(x)=194, x^3-140, x^2-360, x -83 $.
Свойства.
1. Если $ m le n $ при $ a_0ne 0, b_0 ne 0 $, то $ deg q(x) =n-m $ и ведущий член $ q_<>(x) $ равен $ /, x^ $.
2. Если $ g(x)equiv x-c $, то коэффициенты частного $ q_<>(x) $ найдутся из схемы Хорнера.
Наибольший общий делитель
Рассмотрим множество всех общих делителей полиномов $ f_<>(x) $ и $ g_<>(x) $: $$ mathbb D= d_1(x), g(x) mbox < делится на > d_1(x) > . $$ Наибольшим общим делителем полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином $ d_<>(x) $, который является делителем как $ f_<>(x) $, так и $ g_<>(x) $ и, вместе с тем, сам делится на любой другой общий делитель этих полиномов: $$ operatorname (f(x),g(x)) = d(x) iff d(x) in mathbb D , d(x) mbox< делится на > forall d_1(x) in mathbb D . $$ Рассмотрим множество всех полиномов, которые делятся и на $ f_<>(x) $ и на $ g_<>(x) $: $$ mathbb K= f(x), k_1(x) mbox < делится на > g(x) > . $$ Наименьшим общим кратным полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином $ k_<>(x) $, который делится как на $ f_<>(x) $, так и на $ g_<>(x) $ и, вместе с тем, сам является делителем любого другого полинома, который делится на $ f_<>(x) $ и $ g_<>(x) $: $$ operatorname (f(x),g(x)) = k(x) iff k(x) in mathbb K , forall k_1(x) in mathbb K mbox< делится на > k(x) . $$ Пока открытым является вопрос существования $ operatorname (f,g)_<> $ и $ operatorname (f,g)_<> $. Для первого случая этот вопрос решается конструктивно — построением $ operatorname (f,g)_<> $ с помощью алгоритма, позаимствованного из ☞ ТЕОРИИ ЧИСЕЛ.
Пусть $ f(x) not equiv 0 $ и $ g(x) not equiv 0 $ — полиномы из $ mathbb A_<>[x] $ . Поделим $ f_<>(x) $ на $ g_<>(x) $: $ f(x)=g(x)q_<1>(x)+r_1(x) $, пусть остаток $ r_<1>(x) not equiv 0 $, тогда $ 0 le deg r_<1>(x)
Теорема. Последний не равный нулю остаток в алгоритме Евклида совпадает с $ operatorname(f(x),g_<>(x)) $.
Доказательство полностью аналогично доказательству соответствующего результата из теории целых чисел. ♦
Пример. Вычислить
$$ operatorname left( x^4+3, x^3 -x^2 -4, x -3, , 3, x^3 +10, x^2 +2, x -3 right) , . $$
Решение. $$ begin x^4 &+3,x^3 &-x^2 &-4,x &-3 && 3,x^3+10,x^2+2,x-3\ x^4&+10/3, x^3&+2/3, x^2&-, x & && overline < 1/3 x -1/9 quad >\ hline &-1/3,x^3&- 5/3,x^2&-3,x&-3 \ &-1/3,x^3&-10/9,x^2& -2/9,x&<> +1/3 \ hline &&-5/9,,x^2& -25/9,x&-10/3 end $$ В обозначениях алгоритма Евклида, имеем: $$ q_<1>(x)=1/3, x -1/9, r_<1>(x)=-5/9, x^2 -25/9, x-10/3 . $$ Поскольку $ r_<1>(x) notequiv 0 $, делим $ g_<>(x) $ на этот остаток: $$ begin 3,x^3 &+10,x^2 &+2,x &-3 && -5/9,,x^2 -25/9,x-10/3 \ 3, x^3&+15, x^2&+18, x & &&, overline <-27/5, x +9 quad >\ hline &-5,x^2&-16,x&-3 \ &-5,x^2&-25,x&-30 \ hline &&9,x&+27 end $$ Здесь $ q_<2>(x)=-27/5, x +9, r_2(x)=9x+27 notequiv 0 $ и алгоритм деления продолжается: $$ begin -5/9,,x^2& -25/9,x& -10/3 && 9,x+27 \ -5/9,,x^2& -5/3,x& && , overline < -5/81, x – 10/81 quad >\ hline &-10/9,x& -10/3 \ &-10/9,x&-10/3 \ hline & & 0 end $$ Здесь остаток получился равным нулю, следовательно $ r_<2>(x)=operatorname(f(x),g(x)) $.
Ответ. $ 9(x+3)_<> $.
Еще один способ нахождения $ operatorname $ для полиномов из $ mathbb[x] $ вытекает из основной теоремы высшей алгебры.
Теорема. Пусть множество $ < (x-lambda_1),dots,(x-lambda_<mathfrak r>) > $ представляет собой объединение множеств линейных сомножителей полиномов $ f_1(x),dots,f_k(x) $. Выпишем «универсальное» разложение каждого $ f_j $ на линейные сомножители:
Пример. Вычислить $ operatorname left(x^2-1,, x^3+1 right) $ .
Решение. Выписываем разложения полиномов на линейные сомножители: $$x^2-1equiv (x-1)(x+1), quad x^3+1 equiv(x+1) left(x-left( 1/2 — sqrt<3>/2 mathbf right) right) left(x- left( 1/2 + sqrt<3>/2 mathbf right) right) .$$
Ответ. $ x+1 $.
Теорема. Существуют полиномы $ u(x)_<> $ и $ v(x)_<> $ из $ mathbb A[x] $, удовлетворяющие уравнению линейного представления $ operatorname $:
Доказательство этого результата и практический способ построения полиномов $ u(x)_<> $ и $ v(x)_<> $ можно скопировать из соответствующего раздела теории чисел.
Явное представление $ operatorname (f(x),g(x)) $ через коэффициенты полиномов с помощью аппарата определителей приведено ☞ ЗДЕСЬ.
Взаимно простые полиномы
— это полиномы, у которых нормализованный $ operatorname $ равен $ 1_<> $ (тождественно). Подробное рассмотрение этого случая ☞ ЗДЕСЬ.
Производные от полинома
Для случая произвольной функции $ F(x): mathbb R mapsto mathbb R $ это определение строится на предельном переходе: $$ frac bigg|_<_> = F^<prime>(c) = lim_ frac .$$ Пусть $ F(x)equiv x^k $ при $ kin mathbb N_<> $. Тогда, с помощью формулы бинома Ньютона получаем: $$(c+h)^k-c^k=kc^h+C_k^2c^h^2+dots+h^k $$ и $$frac to kc^ quad npu hto 0 . $$ Отсюда следует, что функция $ x^ $ дифференцируема в любой точке $ xinmathbb R_<> $ и ее производная равна $ kx^ $. Обобщим это определение и на комплексную плоскость $ mathbb C^<> $ . Всюду в предыдущих рассуждениях допустим, что и точка $ c_<> $ и приращение $ h_<> $ могут быть комплексными. Окончательный вывод не изменится: формула $$(x^k)^<prime>= kx^ $$ остается справедливой и для $ xin mathbb C_<> $. С помощью этой формулы, а также с помощью основных правил дифференцирования функций: $$ left(F_1pm F_2 right)^<prime>=F_1^<prime>pm F_2^<prime>, left(cFright)^<prime>=cF^<prime>, left(F_1F_2 right)^<prime>=F_1^<prime>F_2+F_1F_2^ <prime>$$ получаем $$ f^<prime>(x)=(a_0x^n+a_1x^+dots+a_x+a_n)^ <prime>= na_0x^+(n-1)a_1x^+dots +a_ . $$ Таким образом, $ f^<prime>(x) $ также будет полиномом над $ mathbb A_<> $ и $ deg f^ <prime>= deg f — 1 $. Кроме того, обобщая по индукции формулу дифференцирования произведения, выводим: $$ left(f_1f_2times dots times f_k right)^<prime>= f_1^<prime>f_2times dots times f_k+f_1f_2^<prime>times dots times f_k+ dots+ f_1f_2times dots times f_k^ <prime>. $$ Если применить ее к формуле разложения полинома на линейные множители, то получим формулу $$ begin f^<prime>(x)&=&a_0(x-lambda_2)(x-lambda_3)times dots times (x-lambda_n)+ \ &+&a_0(x-lambda_1)(x-lambda_3)times dots times (x-lambda_n)+ \ &+ & dots + \ &+& a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_). end $$ Из нее, в частности, следует, что $$ f^<prime>(lambda_j)=a_0(lambda_j-lambda_1)times dots times (lambda_j-lambda_)(lambda_j-lambda_) times dots times (lambda_j-lambda_)= a_0 prod_ <1le k le n atop scriptstyle kne j>(lambda_j — lambda_k) . $$ Последняя формула, впрочем, может быть получена и напрямую из определения производной: $$ f^<prime>(lambda_j)=lim_ frac =lim_ frac . $$ Производные высших порядков вводятся определением $$F^<(k)>(x)= left(F^<(k-1)>(x) right)^ <prime> npu k>1 ; $$ для однотипности обозначений считают также нулевой производной сам полином: $$F^<(0)>(x)= F(x) .$$ В дальнейшем нам пригодится следующая формула Лейбница: $$left(F_1 F_2 right)^<(k)>=sum_^k C_k^j F_1^<(k-j)>F_2^ <(j)>=F_1^<(k)>F_2+ C_k^1F_1^<(k-1)>F_2^ <prime>+ C_k^2F_1^<(k-2)>F_2^<prime prime >+ dots +F_1F_2^ <(k)> , $$ где $ C_k^ $ означает биномиальный коэффициент.
Для полинома $ f(x)_<> $ степени $ n_<> $ имеем: $$f^<(k)>(x)=n(n-1)times dots times (n-k+1)a_0x^+dots+k!a_ npu kle n $$ и $ deg f^ <(k)>= deg f — k $. Очевидно $ f^<(k)>(x)equiv 0 $ при $ k> n_<> $.
Теорема. Простой корень полинома не является корнем его производной. Кратный корень полинома кратности $ mathfrak m $ является корнем его производной кратности $ (<mathfrak m>-1) $.
Доказательство. Если $ x=lambda_<> in mathbb C $ — простой корень для $ f_<>(x) $, то $ f(x)equiv (x-lambda)tilde(x) $ при $ tilde(lambda) ne 0 $. Дифференцируя и подставляя $ x=lambda $, получаем $$ f^<prime>(x)equiv tilde(x) +(x-lambda)tilde^<prime>(x) Rightarrow f^<prime>(lambda)=tilde(lambda)ne 0 $$ по предположению.
Если $ x=lambda_<> $ — кратный корень кратности $ mathfrak m $ для $ f_<>(x) $, то $ f(x)equiv (x-lambda)^<mathfrak m>widehat(x) $ при $ widehat(lambda) ne 0 $. Снова дифференцируем: $$ f^<prime>(x)=<mathfrak m>(x-lambda)^<<mathfrak m>-1> widehat(x)+ (x-lambda)^<<mathfrak m>>widehat^<prime>(x)= (x-lambda)^<<mathfrak m>-1> underbrace<left(<mathfrak m>widehat(x) +(x-lambda)widehat^<prime>(x) right)>_ <= H(x)> . $$ Из этого представления следует, что $ x=lambda_<> $ является корнем $ f^<prime>(x) $ кратности, не меньшей $ (<mathfrak m>-1) $. Если бы кратность была больше этого значения, то необходимо $ H(lambda)=0 $. Однако, этого не может быть, т.к. $ widehat(lambda) ne 0 $. ♦
Полином $ f(x)_<> $ имеет кратный корень тогда и только тогда, когда он имеет нетривиальный наибольший общий делитель со своей производной $$ operatorname (f(x),f^<prime>(x)) notequiv const . $$
Пример. При каком условии на коэффициенты $ p_<> $ и $ q_<> $ полином
$$ x^3+p,x+q $$ имеет кратный корень?
Решение. На основании теоремы на этом корне $ x=lambda_<> $ должно быть выполнено $$lambda^3+p,lambda+q=0 , quad 3, lambda^2 + p=0 .$$ Из второго равенства выражаем $ lambda^2 $ и подставляем в первое: $$lambda^2=-frac
<3> Rightarrow lambda left(-frac
<3>right) +p,lambda+q=0 Rightarrow lambda=-frac<3,q> <2,p>$$ при $ pne 0 $. Подставляя это значение в любое из исходных равенств, получаем: $$ frac<27,q^2+4,p^3> <4, p^2>=0 Rightarrow left(frac <2>right)^2 + left(frac
<3>right)^3 =0 . $$ Это условие уже встречалось нам ВЫШЕ при анализе формулы решения уравнения третьей степени. При $ p=0 $ кратный корень может встретиться лишь при $ q=0 $, т.е. опять же при обращении в нуль дискриминанта кубического уравнения.
Ответ. $ left( p/3 right)^3 + left( q/2 right)^2=0 $.
При каком условии на коэффициенты $ p_<> $ и $ q_<> $ полином
а) $ x^4+p,x+q $ ; б) $ x^5+p,x+q $
имеет кратный корень?
Пример. Найти все значения параметра $ <coloralpha > $, при которых полином
$$ x^4-5,x^2+ <coloralpha >,x+28 $$ имеет кратный корень.
Решение. На основании следствия к теореме для выполнения условия необходимо и достаточно, чтобы был нетривиален $ operatorname (f(x),f^<prime>(x)) $. Ищем его по алгоритму Евклида, делим $ f(x) $ на $ f^<prime>(x) $: $$ f(x)equiv frac<1> <4>, x, f^<prime>(x) + overbrace<left(-frac<5><2>, x^2 +frac<3><4>, <coloralpha >, x +28 right)>^ , $$ затем $ f^<prime>(x) $ на полученный остаток $ r_<1>(x) $: $$ f^<prime>(x) equiv left(-frac<8><5>,x- frac<12><25>, <coloralpha > right) r_1(x) + overbrace<left(frac<3><25>,(3, <coloralpha >^2 + 290),x+ frac<361><25>, <coloralpha > right)>^ , $$ и, при дополнительном предположении $ 3, <coloralpha >^2 + 290ne 0 $, делим $ r_<1>(x) $ на $ r_<2>(x) $: $$ r_1(x) equiv frac<25> <36left(3, <coloralpha >^2 +290 right)^2> left[-30,left(3, <coloralpha >^2 +290 right) x + alpha, (27, <coloralpha >^2 + 6220) right] r_2(x) + $$ $$ + frac <25, left(-27, <coloralpha >^4 -19660, <coloralpha >^2 + 3390912right) > <36, left(3, <coloralpha >^2 +290 right)^2> . $$ $ operatorname (f(x),f^<prime>(x)) $ может быть нетривиальным (равным $ r_<2>(x) $) только при условии $$-27, <coloralpha >^4 -19660, <coloralpha >^2 + 3390912=0 . $$ Решить последнее уравнение легко если заменить переменную $ A = <coloralpha >^2 $: $$( A-144)(27, A +23548)=0 .$$
При $ 3, <coloralpha >^2 + 290= 0 $ будет $ operatorname (f(x),f^<prime>(x))= r_2(x)not equiv 0 $, так что при этих значениях параметра кратных корней у $ f(x)_<> $ быть не может.
Число $ lambda_<> $ является корнем кратности $ mathfrak m_<> $ для $ f(x)_<> $ тогда и только тогда, когда выполнены условия:
Доказательство необходимости следует из теоремы. Достаточность вытекает из результатов следующего пункта (формализация способа проверки приводится ☞ ЗДЕСЬ).
Формула Тейлора
Представление полинома $ f(x)_<>in mathbb A[x] $ в канонической форме $ a_<0>x^n+a_1x^+dots + a_n $ не является единственно возможным способом задания полинома. В конце концов, полином можно представить и с помощью разложения на линейные сомножители — разумеется, если известен набор его корней. Саму эту каноническую форму можно описать как разложение полинома по степеням переменной $ x_<> $. Пусть теперь $ cin mathbb A_<> $ — произвольная константа. Любую степень $ x^ $ можно «переразложить» по степеням линейного полинома $ x-c_<> $ с помощью формулы бинома Ньютона: $$ x^kequiv left[c+(x-c) right]^kequiv c^k +kc^(x-c)+ frac<2>c^(x-c)^2+dots+ (x-c)^k .$$ Если это сделать для каждого монома полинома $ f(x)_<> $, то получим разложение $ f(x)_<> $ по степеням $ x-c_<> $ в виде $$ f(x)equiv A_0+A_1(x-c)+A_2(x-c)^2+dots+A_n(x-c)^n . $$
Задача. Найти коэффициенты $ A_<0>,dots,A_n $ в этом разложении.
Для решения этой задачи продифференцируем несколько раз последнее тождество: $$ begin f^<prime>(x)&=&A_1+2,A_2(x-c)+3,A_3(x-c)^2+dots+nA_n(x-c)^ , ,\ f^<prime prime>(x)&=&2,A_2+3cdot 2,A_3(x-c)+dots +n(n-1)A_n(x-c)^, ,\ f^<prime prime prime>(x)&=&3cdot 2,A_3+dots +n(n-1)(n-2)A_n(x-c)^, ,\ dots & & dots end $$ Подстановка в эти формулы $ x=c_<> $ дает: $$f^<prime>(c)=A_1, f^<prime prime>(c)=2,A_2, f^<prime prime prime>(c)= 3cdot 2,A_3,dots $$
Теорема. Разложение полинома $ f_<>(x) $ по степеням $ x-c_<> $ имеет вид
$$ f(x) equiv f(c)+ frac(c)> <1!>(x-c) + frac(c)> <2!>(x-c)^2+ dots + frac(c)> (x-c)^ = $$ $$ =sum_^n frac(c)> (x-c)^ ; $$ это тождество называется формулой Тейлора для полинома $ f_<>(x) $ в точке $ x=c $.
Доказательство и алгоритм эффективного вычисления коэффициентов формулы Тейлора (схема Хорнера) ☞ ЗДЕСЬ.
На основании этих серий мы должны предсказать величину $ F(x)_<> $. Самой простой функцией, решающей задачи в таких постановках, является полином. Если этот полином $ f(x)_<> $ удается построить, то именно его мы и будем считать приближением неизвестной нам функции $ F(x)_<> $. Задача построения такого полинома для серии экспериментов первого типа обсуждается ☞ ЗДЕСЬ. А формула Тейлора позволяет найти полином $ f(x)_<> $ для серии экспериментов второго типа. Геометрически: неизвестный нам заранее график функции $ y=F(x)_<> $ (красный) приближается (аппроксимируется) либо прямой (зеленый), либо параболой (серый), либо кубикой (фиолетовый) — и все кривые приближения строятся только на основании информации о функции $ F(x)_<> $ в одной-единственной точке $ c_<> $.
Пример. Найти приближенное значение $ F(1)_<> $, если известно, что
Решение. По формуле Тейлора получаем полином $$f(x)=0.367+0.367(x+1) + frac<0.367> <2>(x+1)^2+frac<0.367> <6>(x+1)^3 $$ и $ f(1)=2.324(3) $.
Ответ. $ F(1)approx 2.324 $.
Полиномы с вещественными коэффициентами
Рассмотрим теперь случай полинома с вещественными коэффициентами $ f(x)=a_0x^n+a_1x^+ dots + a_n in mathbb R [x] $.
Теорема. Значения полинома $ f(x) in mathbb R [x] $ от комплексно-сопряженных значений переменной будут также комплексно-сопряженными:
$$ mbox <если> f(c)=A+mathbf i B mbox <при> subset mathbb R, mbox <то> f(overline)=A-mathbf i B , . $$
Доказательство. Действительно, поскольку $ a_jin mathbb R $, то $ overline=a_j $ для $ forall jin <0,1,dots,n>$, и тогда $$ begin fleft(overline right)&=&a_0 overline^n + a_1 overline^ + dots + a_n = overline overline + overline overline>+ dots + overline= \ &=&overline+ dots + a_n>=A-mathbf i B . end $$
Если мнимое число $ c=alpha + mathbf i beta , beta ne 0 $ является корнем $ f_<>(x) $, то и ему комплексно-сопряженное $ overline c = alpha — mathbf i beta $ также является корнем $ f_<>(x) $.
Иными словами, мнимые корни полинома $ f_<>(x) $ с вещественными коэффициентами «ходят пáрами»: $ alpha pm mathbf i beta $. Геометрический смысл: на комплексной плоскости точки, изображающие корни $ f_<>(x) $, расположены симметрично относительно вещественной оси.
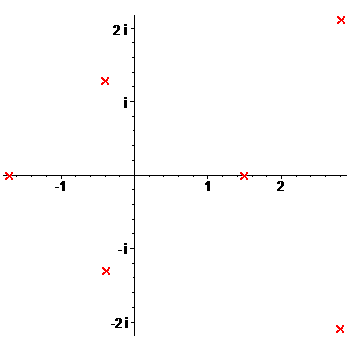
Как следствие предыдущей теоремы и основной теоремы высшей алгебры, получим
Теорема. Любой полином $ f_<>(x)in mathbb R [x] $ может быть представлен в виде произведения вещественных полиномов степеней не выше второй:
$$ begin f(x) & equiv a_0 (x- lambda_1)^<<mathfrak m>_1> times dots times (x- lambda_r)^<<mathfrak m>_r> times \ & times (x^2 +p_1x+ q_1)^<<mathfrak M>_1> times dots times (x^2 +p_<ell>x+ q_<ell>)^<<mathfrak M>_<ell>> . end $$ Здесь $ lambda_1 , dots , lambda_r $ — различные вещественные числа, а квадратные трехчлены $$ x+ q_<ell>> subset mathbb R [x] $$ — различные с отрицательными дискриминантами $ mathcal D_j=p_j^2-4q_j
Полином $ f_<>(x) $ с вещественными коэффициентами нечетной степени имеет хотя бы один вещественный корень, а, в общем случае, нечетное число вещественных корней (с учетом их кратностей ).
Геометрия
Полиномы с вещественными коэффициентами удобны тем, что теоретические результаты, полученные в предыдущих пунктах, получают геометрическую интерпретацию. Прежде всего, следует отметить, что полином является частным случаем непрерывной функции и на него распространяются все результаты математического анализа, разработанные для подобных функций. Итак, полином $ f_<>(x) $ — непрерывная функция при любых $ x in mathbb R $. Более того, поскольку производные полинома снова оказываются полиномами, то свойство непрерывности наследуется при дифференцировании: полином является непрерывно-дифференцируемой функцией. Из этого следует, что на плоскости $ (x_<>,y) $ график полинома $ y=f_<>(x) $ представляет из себя непрерывную и гладкую кривую (ни разрывов, ни углов!) — касательная к графику существует в любой его точке.
Далее, вещественному корню $ x=lambda_<> $ полинома $ f_<>(x) $ на плоскости $ (x_<>,y) $ соответствует точка пересечения графика $ y=f_<>(x) $ с осью абсцисс.
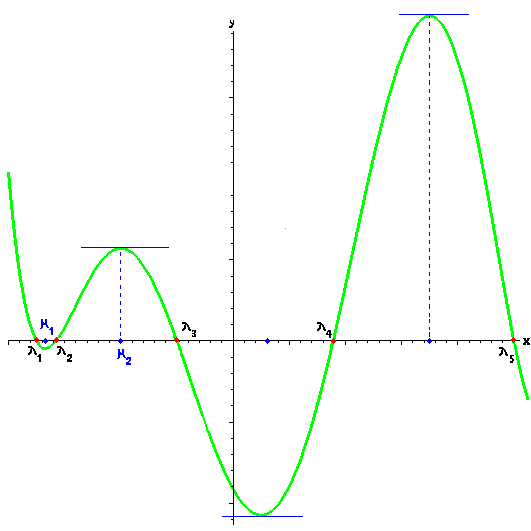
По основной теореме высшей алгебры, таких точек может быть только конечное число: их — не более степени полинома $ deg f (x) $. Далее, между каждой парой $ lambda_j, lambda_k $ вещественных корней полинома $ f_<>(x) $, его график обязан иметь «впадину» или «горб». Обращаясь к языку математического анализа, можно сказать (и доказать), что между двумя вещественными корнями полинома находится точка его локального минимума или локального максимума. В этой точке касательная к графику функции параллельна оси абсцисс и, следовательно, тангенс угла наклона касательной должен быть равен нулю. Иными словами, точки $ mu_1,mu_2,dots $, в которых полином имеет локальный минимум или максимум, должны быть корнями его производной. См. следующий ПУНКТ.
К сожалению, не имеется наглядной интерпретации мнимых корней полинома .
Дальнейшие геометрические свойства полинома с вещественными коэффициентами см. ☞ ЗДЕСЬ.
Экстремумы
Говорят, что полином $ f(x)in mathbb R[x] $ имеет в точке $ c_<> $ (локальный) минимум если существует некоторое $ delta>0 $, что при всех значениях аргументов из $ delta_<> $-окрестности точки $ c_<> $, т.е. при всех $ x_<> $, удовлетворяющих неравенству $ |x-c| f(c) $. Если последнее неравенство изменить на противоположное, то получим определение (локального) максимума. Говорят, что полином имеет в точке $ c_<> $ (локальный) экстремум 10) если он имеет в этой точке либо максимум либо минимум.
Теорема [Ферма для полиномов]. Если полином $ f_<>(x) $ имеет в точке $ c_<> $ экстремум, то в этой точке его производная обращается в нуль: $$ f'(c)=0 . $$
Геометрический смысл этого результата пояснен в предыдущем пункте. Обращение производной полинома в нуль в точке $ c_<> $ является условием необходимым для существования в ней экстремума. Для выяснения будет ли в этой точке минимум, максимум или же экстремум отсутствует, следует обратиться к формуле Тейлора. Рассмотрим эту формулу в точке $ c_<> $ «подозрительной на экстремум», т.е. в такой, где $ f'(c)=0 $: $$ f(x)-f(c)=frac<1><2>f»(c)(x-c)^2+frac<1><6>f»'(c)(x-c)^3+dots+frac<1>f^<(n)>(c)(x-c)^n . $$ Если $ f»(c)ne 0 $, то можем переписать эту разность в виде $$ f(x)-f(c)=(x-c)^2underbrace<left[frac<1><2>f»(c)+frac<1><6>f»'(c)(x-c)+dots+frac<1>f^<(n)>(c)(x-c)^right]>_ . $$ Полином $ P(x) $ в точке $ c_<> $ имеет значение $ frac<1><2>f»(c) $, и его знак в некоторой окрестности точки $ c_<> $ полностью определяется знаком этого числа. Таким образом, в той же окрестности имеем: $$ operatorname (f(x)-f(c)) = operatorname (f»(c)) . $$
Если в точке $ c_<> $ выполнены условия $ f'(c)=0, f»(c)> 0 $ то в этой точке полином имеет локальный минимум; если же в ней выполнены условия $ f'(c)=0, f»(c) c \ — operatorname f»'(c) quad npu x нечетном $ k_<> $. При этом в точке $ c_<> $ полином будет иметь локальный минимум при $ f^<(k+1)>(c)>0 $ и локальный максимум при $ f^<(k+1)>(c) ☞ ЗДЕСЬ ), поэтому оценить корни полинома $ f'(x) $ мы можем, разве что, приближенно. После их нахождения, приближеные значения подставляются в полином $ f_<>(x) $ и ошибка вычислений накапливается… Можно ли избежать этого накопления? — Частично, да. Для полинома $ f_<>(x) $ (четной) степени $ n_<> $ можно построить новый полином степени $ n-1 $ по новой переменной $ z_<> $: $$ mathcal F(z) = (z-f(mu_1))times dots times(z-f(mu_)) , $$ где $ mu_1,dots,mu_ $ — корни $ f'(x) $. При этом коэффициенты нового полинома $ mathcal F(z) $ будут рационально выражаться через коэффициенты полинома $ f'(x) $ на основании теоремы Гаусса о симметрических полиномах. Подробности конструктивного построения см. ☞ ЗДЕСЬ. Как правило, максимальный вещественный корень полинома $ mathcal F(z) $ и будет давать значение $ max f(x) $.
Пример. Найти $ displaystyle max_ (-x^6+12,x^2+12,x+2) $.
Решение. Если идти по традиционной схеме математического анализа, то мы должны сначала найти корни производной полинома $ f(x)=-x^6+12,x^2+12,x+2 $, т.е. решить уравнение $ x^5-4,x-2=0 $. В радикалах это уравнение не решается, так что приходится применять приближенные методы поиска вещественных корней: $ mu_1approx -1.24359, mu_2 approx — 0.50849, mu_3 approx 1.51851 $. Наконец, требуется сравнить по величине $ f(mu_1), f(mu_2), f(mu_3) $.
В альтернативу этому подходу, можно избежать нахождения корней производной и построить (хоть и кропотливо, но зато безошибочно) полином $$ mathcal F(z)= -z^5+10,z^4+472,z^3+16208,z^2-16272,z-32800 , $$ найти один его (максимальный вещественный) корень $ approx 35.6321 $ — он и будет искомым максимумом.
Проверка: $ max f = f(mu_3) approx 35.6321 $.
Подчеркнем, что указанная возможность гарантирована только полиномиальностью рассматриваемой экстремальной задачи и на произвольные (неполиномиальные) функции предлагаемый метод не распространяется.
Приводимость
Полином $ Phi(x) in mathbb A[x] $, отличный от константы, называется неприводимым в (или неприводимым над) $ mathbb A_<> $ если у $ Phi(x) $ нет нетривиального делителя в $ mathbb A[x] $. В противном случае $ Phi(x) $ называется приводимым в (или приводимым над) $ mathbb A_<> $. Полином $ Phi(x) in mathbb A[x] $ неприводим над $ mathbb A_<> $ тогда и только тогда, когда $ operatorname (Phi(x),g(x)) equiv const in mathbb A_<> $ для любого полинома $ g(x)in mathbb A_<>[x], deg g(x) ♦
Теорема. Любой полином $ f(x)in mathbb R [x] $ степени большей $ 2_<> $ приводим в $ mathbb R_<> $. Неприводимыми в $ mathbb R_<> $ являются полиномы вида
$$ x+a quad mbox <и>quad x^2+p, x +q_<> quad mbox <при>quad subset mathbb R, p^2 — 4q ☞ ЗДЕСЬ .
Рассмотрим теперь полином с рациональными коэффициентами: $$f(x)=a_0x^n+a_1x^+dots+a_n in mathbb Q [x] , a_0 ne 0 . $$ Если полином $ f_<>(x) $ приводим в $ mathbb Q_<> $, то будет приводимым и полином $ Ccdot f_<>(x) $ при $ forall C in mathbb Q, C ne 0 $; верно и обратное. Представив коэффициенты $ a_<0>,dots, a_n $ в виде несократимых дробей, возьмем $$ C=operatorname(mbox< знаменатель > a_<0>,dots, mbox< знаменатель > a_n ) , $$ тогда приводимость (или неприводимость) полинома $ f_<>(x) $ в $ mathbb Q_<> $ эквивалентна приводимости (соответственно, неприводимости) в $ mathbb Q_<> $ полинома $ Ccdot f(x) $ с целыми коэффициентами. Поэтому в дальнейшем будем сразу предполагать $ f(x)in mathbb Z[x] $. Можно ли пойти дальше и утверждать, что приводимость такого полинома в $ mathbb Q_<> $ эквивалентна приводимости его в $ mathbb Z_<> $, т.е. полином раскладывается на произведение полиномов меньших степеней с рациональными коэффициентами тогда и только тогда, когда он раскладывается на произведение полиномов меньших степеней с целыми коэффициентами?
Теорема. Полином $ f(x)in mathbb Z[x] $ неприводимый в $ mathbb Z_<> $ будет неприводимым и в $ mathbb Q_<> $.
Приводимость полинома с целыми коэффициентами $ f(x)in mathbb Z[x] $ в $ mathbb Z_<> $ означает, что он раскладывается на два множителя с целыми коэффициентами: $$ a_0x^n+a_1x^+ dots + a_n equiv (b_0x^k+b_1x^ + dots + b_k) (c_0x^<ell>+c_1x^ <ell-1>+ dots + c_<ell>) $$ при $ k ☞ ЗДЕСЬ . ♦
Итак, для поиска рациональных корней полинома $ f_<>(x) $ надо выписать множество всех натуральных делителей $ <<mathfrak p>_1=1,dots,<mathfrak p>_> $ числа $ |a_n| $, и множество всех натуральных делителей $ <<mathfrak q>_1=1,dots,<mathfrak q>_> $ числа $ |a_0| $, и после этого организовать вычисление $ fleft(pm <mathfrak p>_j/<mathfrak q>_i right) $ при всех возможных значениях индексов $ jin <1,dots,s >, i in <1,dots, t >$. Если ни одно из полученных чисел не равно нулю, то рациональных корней полином не имеет.
Если нормализованный полином $ f(x) in mathbb Z[x] $ имеет рациональные корни, то они — только целые и находятся среди делителей свободного члена.
Пример. Найти рациональные корни полинома
Подробнее о приводимости и неприводимости полиномов в $ mathbb Z_<> $ ☞ ЗДЕСЬ.
Локализация корней
Границы расположения корней
Теорема [Маклорен]. 11) Все корни полинома
$$f(x)=a_0x^n+a_1x^+dots+a_n in mathbb C [x], a_0 ne 0$$ удовлетворяют неравенству $$ |lambda_j| 0$$ удовлетворяют неравенству $$ lambda_j положительные корни.
А как получить нижнюю оценку возможных отрицательных корней?
Это можно сделать с помощью преобразования 1 полинома, рассмотренного ☞ ЗДЕСЬ. В самом деле, отрицательные корни полинома $ f(x) $ являются положительными корнями полинома $ f(-x) $. Найдя верхнюю границу последних с помощью любого из приведенных выше критериев, мы меняем у нее знак и в результате получаем нижнюю оценку отрицательных корней $ f(x) $. Преобразование 3 , рассмотренное в том же пункте, позволяет получить отдельные интервалы для возможных положительных и отрицательных корней.
Пример. Найти оценки положительных и отрицательных корней полинома
$$ f(x)=x^8+2, x^7-2, x^6 +6, x^5 -80, x^4 + 100, x^3 -400, x^2 + 15, x +30 . $$
Решение. Сначала ограничим положительные корни сверху. В теореме Лагранжа имеем $ r=2,, A=400 $, следовательно $ lambda_j -401 $. Формируем полином $$ f^<ast>(x) = x^8f(1/x)= 1+2, x-2, x^2 +6, x^3 -80, x^4 + 100, x^5 -400, x^6 + 15, x^7 +30,x^8 $$ для оценки нижней границы положительных корней: $$1/lambda_j frac<1><1 +sqrt<40/3>> . $$ Наконец, оценка Лагранжа для полинома $ f^<ast>(-x) $: $$-1/lambda_j 12) .
Теорема [Декарт]. Число положительных корней полинома
$$f(x)=a_0x^n+a_1x^+dots+a_x+a_n in mathbb R[x], quad (a_0> 0,a_n ne 0)$$ с учетом их кратностей равно или меньше на четное число числа знакоперемен в ряду его коэффициентов: $$ operatorname < f(x)=0 mid x>0 > = <mathcal V>(a_0,a_1,dots,a_n)-2 k , quad kin <0,1,2, dots > . $$
Доказательство ☞ ЗДЕСЬ.
С помощью преобразования корней полинома (см. пункт 1 ☞ ЗДЕСЬ ) можно доказать следствие:
Число отрицательных корней полинома
$$f(x)=a_0x^n+a_1x^+dots+a_x+a_n, quad (a_0> 0,a_n ne 0)$$ с учетом их кратностей можно оценить по формуле $$ operatorname < f(x)=0 mid x 0 >=2-2k ge 0 ,$$ следовательно $ f_<>(x) $ имеет либо два, либо ни одного положительного корня. Далее, по следствию: $$ operatorname < f(x)=0 mid x
Если каким-то образом заранее известно, что все корни полинома вещественны, то число положительных из них определяется по правилу знаков Декарта однозначно:
Пример. Характеристический полином вещественной симметричной матрицы удовлетворяет условию следствия. См. ☞ ЗДЕСЬ.
Корни полинома в областях комплексной плоскости
Задача. Для полинома 14) $ f(z) $ получить точную информацию о числе его корней в заданной области $ mathbb S $ комплексной плоскости $ mathbb C $.
Оказывается, для достаточно широкого класса областей $ mathbb S $ эту информацию можно получить без применения численных, т.е. приближенных методов. Существуют алгоритмы, позволяющие за конечное число элементарных алгебраических операций ($ +,-,times, div $) над коэффициентами $ f(z) $ установить количество корней этого полинома в таких областях, как, к примеру, $$ begin mathbb S&=&< zin mathbb R big| a 15) на заданном интервале $ ]a,b[ $ если на этом интервале
1. cоседние полиномы $ f_j(x) $ и $ f_(x) $ не имеют общих корней;
2. $ f_K(x)ne 0 $;
3. если $ f_j(x_0)=0 $ при $ x_0 in ]a,b[ $ и $ jin <1,dots,k-1>$, то числа $ f_(x_0) $ и $ f_(x_0) $ имеют разные знаки: $ f_(x_0)f_(x_0) 4. произведение $ f_<0>(x)f_<1>(x) $ меняет знак с отрицательного на положительный когда $ x_<> $, возрастая, проходит корень $ lambdain ]a,b[ $ полинома $ f_0(x)equiv f(x) $.
Число знакоперемен $$ <mathcal V>_x= <mathcal V>(f_0(x), f_1(x),dots, f_K(x)) $$ при $ x_<> $ возрастающем от $ a_<> $ к $ b_<> $, будет меняться когда $ x_<> $ проходит через корень какого-либо полинома системы. Доказывается, что это число может разве лишь уменьшаться, и уменьшается на единицу тогда и только тогда, когда $ x_<> $ проходит через корень начального полинома системы, т.е. через корень $ f(x)_<> $.
Теорема [Штурм]. Если $ f(a)ne 0, f(b)ne 0 $, и система $ f_0(x), f_1(x),dots, f_K(x) $ является системой полиномов Штурма для $ f(x_<>) $, то
$$ operatorname $. Оказывается, что в качестве полиномов системы Штурма можно взять последовательность остатков из алгоритма Евклида, если только домножить некоторые из них на $ -1_<> $. Именно, возьмем $$f_1(x) equiv f'(x) .$$ Поделим $ f_<0>(x) equiv f(x) $ на $ f_<1>(x) $ и обозначим через $ f_<2>(x) $ остаток, домноженный на $ -1_<> $: $$f_0(x)equiv q_1(x) f_1(x)-f_2(x), quad deg f_2 ☞ ЗДЕСЬ
Левая полуплоскость: устойчивость
Полином $ f(z) $ с комплексными коэффициентами называется устойчивым, если все его корни удовлетворяют условию $ <mathfrak Re>(z) 0 $ необходимо и достаточно, чтобы были выполнены неравенства
$$ a_1>0, left| begin a_1 & a_3 \ a_0 & a_2 end right|>0, left| begin a_1 & a_3 & a_5\ a_0 & a_2 & a_4 \ 0 & a_1 & a_3 end right|>0,dots, left| begin a_1 & a_3 & a_5 & dots & 0\ a_0 & a_2 & a_4 & dots & 0 \ 0 & a_1 & a_3 & dots & 0 \ 0 & a_0 & a_2 & dots & 0 \ dots & & & ddots & dots \ dots & & & dots & a_n end right|>0 . $$
Единичный круг
Единичным кругом на комплексной плоскости назовем круг $ |z|le 1 $.
Задача. Найти необходимые и достаточные условия на коэффициенты полинома $ f(z)=a_0z^n+dots+ a_n $, при которых все его корни $ lambda_1,dots, lambda_n $ находятся внутри единичного круга, т.е. удовлетворяют условию $ |z| 0, A_1>0, A_2>0, A_3>0, A_1A_2-A_0A_3>0 ; $$ и $$A_0 0 .$$ Подставляя сюда выражения для коэффициентов, получим, что первая система ограничений имеет решение $ -1 |mbox < свободный член >f(z)| , $$ т.е. $ |a_0| > |a_n| $, и полином $$ f_1(z) = frac(z)> quad npu quad f^<*>(z) = z^nf(1/z) equiv a_0+a_1z+dots+a_nz^n $$ имеет все свои корни лежащими внутри единичного круга.
На первый взгляд, конструктивность этого результата не очень очевидна: исходная задача для полинома $ f(z) $ сводится к аналогичной задаче для полинома $ f_1(z) $. Обратим, однако, внимание на то, что полином $$ begin f_1(z)&=& left[a_0(a_0z^n+dots+a_n)-a_n (a_0+a_1z+dots+a_nz^n) right] big/ z = \ &=& left[(a_0^2-a_n^2)z^n+(a_0a_1-a_a_n)z^ + dots + (a_0a_-a_<1>a_n)z right] big/ z = \ &=& (a_0^2-a_n^2)z^+(a_0a_1-a_a_n)z^ + dots + (a_0a_-a_<1>a_n) end $$ имеет степень меньшую, чем $ deg f $. Таким образом, алгоритм конструктивен в том смысле, что он сводит исходную задачу к более простой. Применяя к полиному $ f_1(z) $ снова критерий Шура-Кона, получим следующее необходимое условие $$ |mbox < старший коэффициент >f_1(z) | > | mbox < свободный член >f_1(z)| iff quad |a_0^2-a_n^2| > |a_0a_-a_<1>a_n| , $$ при выполнении которого дальнейшему исследованию подлежит полином $$ f_2(z) = frac<(a_0^2-a_n^2)f_1(z)-(a_0a_-a_<1>a_n)f^<*>_1(z)> . $$ Продолжая процедуру, за конечное число шагов мы дойдем до полинома первой степени. Окончательно, необходимые и достаточные условия нахождения всех корней полинома $ f(z) $ степени $ n_<> $ внутри единичного круга получаются объединением $ n_<> $ условий $$ |mbox < старший коэффициент >f(z) |>|mbox < свободный член >f(z)| , $$ $$ |mbox < старший коэффициент >f_1(z) | > |mbox < свободный член >f_1(z)| , $$ $$ vdots qquad qquad qquad vdots $$ $$ |mbox < старший коэффициент >f_(z) |>|mbox < свободный член >f_(z)| . $$
Пример на применение этой теоремы ☞ ЗДЕСЬ.
Численные методы поиска корней полинома
Как упоминалось ☝ ВЫШЕ, корни полинома $ f_<>(z) $, как правило, не выражаются в радикалах уже при $ deg f=5 $ . Но даже в тех случаях, когда выражаются, как, например, $$lambda=frac<sqrt<5>-1 + sqrt<10- sqrt<20>>> <2>quad mbox < для > f(x)=x^4+2x^3-6x^2-2x+1 , $$ толку от такого представления мало: на каком интервале вещественной оси лежит $ lambda $? Поэтому наряду с поиском аналитических формул для корней полиномов практический интерес представляет нахождение их приближенных значений. Эту задачу будем решать, в основном, для полиномов над $ mathbb R_<> $ (т.е. полиномов с вещественными коэффициентами), с которыми чаще всего и приходится иметь дело на практике.
Нас, прежде всего, будут интересовать именно вещественные корни полиномов. В дальнейшем переменную этих полиномов будем обозначать через $ x_<> $ и считать ее вещественной. Для поиска вещественных корней полинома, как правило, требуется их предварительно отделить, т.е. найти интервалы $ ]a,b_<>[ $, каждый из которых содержит только один корень $ f_<>(x) $. Поиск такого интервала можно производить разными способами, самый общий из которых изложен ☝ ВЫШЕ. Однако, для предварительного понимания изложенных ниже методов, достаточно будет ориентироваться на теорему Больцано: полином имеет корень на $ ]a,b_<>[ $, если на концах интервала он принимает значения разных знаков. Этот корень будет единственным, если дополнительно предположить, что функция $ f_<>(x) $ монотонна на $ ]a,b_<>[ $. Последнее условие будет очевидно выполнено, если производная $ f^<prime>(x) $ не меняет знака на $ ]a,b_<>[ $, т.е. полином $ f^<prime>(x) $ не имеет корней на рассматриваемом интервале. Действительно, если предположить существование двух корней у $ f_<>(x) $ на $ ]a,b_<>[ $, то, по соображениям, упомянутым ☞ ЗДЕСЬ 16) , должна существовать точка этого интервала, в которой $ f^<prime>(x) $ обращается в нуль. Анализ знака $ f^<prime>(x) $ на $ ]a,b_<>[ $ часто удается произвести элементарными рассуждениями.
Как найти сумму коэффициентов в уравнении многочлена
Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.
Решите уравнение: `x^3 +4x^2 — 2x-3=0`.
Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:
`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`
Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.
Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.
Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что
`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.
Умножим обе части на `q^n`, получаем:
`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.
Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:
Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.
Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.
Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.
а) `x^4+4x^3-102x^2-644x-539=0`; (15)
б) `6x^4-35x^3+28x^2+51x+10=0`. (16)
а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:
Поэтому `p` может принимать значения:
Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:
Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:
1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.
2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.
б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in<+-1;+-2;+-5;+-10>`; `qin<1;2;3;6>`.Возможные варианты для `x_0`:
Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем
Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:
Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.
К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.
Разложите на множители:
а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`
Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:
в) Вынесем `x^2` за скобки и сгруппируем:
Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:
В итоге получаем:
Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).
г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению
Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.
Прибегнем к методу неопределённых коэффициентов. Пусть
Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:
Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:
Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.
Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:
2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:
Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.
Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому
Далее каждый из квадратных трёхчленов можно разложить на множители.
Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.
Многочлены
Определения и примеры
Многочлен — это сумма одночленов.
Например, выражение 2x + 4xy 2 + x + 2xy 2 является многочленом. Проще говоря, многочлен это несколько одночленов, соединенных знаком «плюс».
В некоторых многочленах одночлены могут соединяться знаком «минус». Например, 3x − 5y − 2x . Следует иметь ввиду, что это по-прежнему сумма одночленов. Многочлен 3x − 5y − 2x это сумма одночленов 3x , −5y и − 2x , то есть 3x + (−5y) + (−2x) . После раскрытия скобок образуется многочлен 3x − 5y − 2x .
Соответственно, рассматривая по отдельности каждый одночлен многочлена, его нужно рассматривать вместе со знаком, который перед ним располагается. Так, в многочлене 3x − 5y − 2x минус перед одночленом 5y относится к коэффициенту 5 , а минус перед одночленом 2x относится к коэффициенту 2 . Чтобы не противоречить определению многочлена, вычитание можно заменять сложением:
Но это действие нагромождает многочлен скобками, поэтому вычитание на сложение не заменяют, учитывая в будущем, что каждый одночлен многочлена будет рассматриваться вместе со знаком, который перед ним располагается.
Одночлены, из которых состоит многочлен, называют членами многочлена.
Если многочлен состоит из двух членов, то такой многочлен называют двучленом. Например, многочлен x + y является двучленом.
Если многочлен состоит из трёх членов, то такой многочлен называют трехчленом. Например, многочлен x + y + z является трехчленом.
Если какой-нибудь многочлен содержит обычное число, то это число называют свободным членом многочлена. Например, в многочлене 3x + 5y + z + 7 член 7 является свободным членом. Свободный член многочлена не содержит буквенной части.
Многочленом также является любое числовое выражение. Так, следующие выражения являются многочленами:
Сложение многочленов
К многочлену можно прибавить другой многочлен. Например, прибавим к многочлену 2x + y многочлен 3x + y.
Заключим в скобки каждый многочлен и соединим их знаком «плюс», указывая тем самым, что мы складываем многочлены:
Теперь раскрываем скобки:
Далее приведём подобные слагаемые:
Таким образом, при сложении многочленов 2x + y и 3x + y получается многочлен 5x + 2y.
Разрешается также сложение многочленов в столбик. Для этого их следует записать так, чтобы подобные слагаемые располагались друг под другом, затем выполнить самó сложение. Решим предыдущий пример в столбик:
Если в одном из многочленов окажется слагаемое, которое не имеет подобного слагаемого в другом многочлене, оно переносится к результату без изменений. Как говорят при сложении обычных чисел — «сносится».
Например, сложим в столбик многочлены 2x 2 + y 3 + z + 2 и 5x 2 + 2y 3 . Для начала запишем их так, чтобы подобные слагаемые располагались друг под другом, затем выполним их сложение. Обнаруживаем, что во втором многочлене не содержатся слагаемые, которые можно было бы сложить со слагаемыми z и 2 из первого многочлена. Поэтому слагаемые z и 2 переносятся к результату без изменений (вместе со своими знаками)
Решим этот же пример с помощью скобок:
Пример 3. Сложить многочлены 7x 3 + y + z 2 и x 3 − z 2
Решим этот пример в столбик. Запишем второй многочлен под первым так, чтобы подобные слагаемые располагались друг под другом:
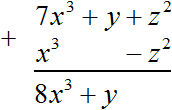
Во втором многочлене не было слагаемого, которого можно было бы сложить со слагаемым y из первого многочлена, поэтому это слагаемое было перенесёно к результату без изменений. А сложение подобных слагаемых z 2 и −z 2 дало в результате 0 . Ноль по традиции не записываем. Поэтому окончательный ответ это 8x 3 + y.
Решим этот же пример с помощью скобок:
Вычитание многочленов
Из многочлена можно вычесть другой многочлен. Например, вычтем из многочлена 2x + y многочлен 3x + y .
Заключим в скобки каждый многочлен и соединим их знаком «минус», указывая тем самым, что мы выполняем вычитание:
Теперь раскроем скобки:
Приведём подобные слагаемые. Слагаемые y и −y являются противоположными. Сумма противоположных слагаемых равна нулю
Приводя подобные слагаемые, мы обычно складываем их. Но в качестве знака операции можно использовать знак одночлена. Так, приводя подобные слагаемые y и −y мы сложили их по правилу приведения подобных слагаемых. Но можно не складывая, записать их друг за другом
Получится тот же результат, поскольку выражения y + (−y) и y − y одинаково равны нулю:
Возвращаемся к нашему примеру. Вычеркнем члены y и −y :
А сложение подобных слагаемых 2x и −3x , даст в результате −x
Или без сложения, записав члены друг за другом:
Значит, при вычитании из многочлена (2x + y) многочлена (3x + y) получится одночлен −x .
Решим этот же пример в столбик:
Пример 2. Вычесть из многочлена 13x − 11y + 10z многочлен −15x + 10y − 15z
Решим этот пример с помощью скобок, а затем в столбик:
Следует быть внимательным при вычитании в столбик. Если не следить за знаками, вероятность допустить ошибку очень высокá. Нужно учитывать не только знак операции вычитания, но и знак располагающийся перед слагаемым.
Так, в данном примере из слагаемого 10z вычиталось слагаемое −15z
Результат вычисления этого выражения должен быть положительным, поскольку 10z − (−15z) = 10z + 15z .
Складывая или вычитая многочлены при помощи скобок, первый многочлен в скобки можно не заключать. Так, в данном примере из многочлена 13x − 11y + 10z требовалось вычесть многочлен −15x + 10y − 15z
Вычитание было записано так:
Но первый многочлен можно не заключать в скобки:
Заключение первого многочлена в скобки на первых порах позволяет начинающим наглядно увидеть, что второй многочлен полностью вычитается из первого, а не из определенной его части.
Представление многочлена в виде суммы или разности
Многочлен можно представить в виде суммы или разности многочленов. По сути это обратное действие раскрытию скобок, поскольку идея подразумевает, что имеется некий многочлен, и из него можно образовать сумму или разность многочленов, заключив в скобки некоторые из членов исходного многочлена.
Пусть имеется многочлен 3x + 5y + z + 7 . Представим его в виде суммы двух многочленов.
Итак, из членов исходного многочлена нужно образовать два многочлена, сложенные между собой. Давайте заключим в скобки члены 3x и 5y , а также члены z и 7 . Далее объединим их с помощью знака «плюс»
Значение исходного многочлена при этом не меняется. Если раскрыть скобки в получившемся выражении (3x + 5y) + (z + 7) , то снова получим многочлен 3x + 5y + z + 7 .
В скобки также можно было бы заключить члены 3x, 5y, z и прибавить это выражение в скобках к члену 7
Представляя многочлен в виде разности многочленов, нужно придерживаться следующего правила. Если члены заключаются в скобки после знака минуса, то этим членам внутри скобок нужно поменять знаки на противоположные.
Вернемся к многочлену 3x + 5y + z + 7 . Представим его в виде разности двух многочленов. Давайте заключим в скобки многочлен 3x и 5y , а также z и 7, затем объединим их знаком «минус»
Но мы видим, что после знака минуса следует заключение членов z и 7 в скобки. Поэтому этим членам нужно поменять знаки на противоположные. Делать это нужно внутри скобок:
Заключая члены в скобки, нужно следить за тем, чтобы значение нового выражения тождественно было равно предыдущему выражению. Этим и объясняется замена знаков членов внутри скобок. Если в выражении (3x + 5y) − (−z − 7) раскрыть скобки, то получим изначальный многочлен 3x + 5y + z + 7 .
Вообще, представляя многочлен в виде суммы или разности, можно придерживаться следующих правил:
Если перед скобками ставится знак «плюс», то все члены внутри скобок записываются со своими же знаками.
Если перед скобками ставится знак «минус», то все члены внутри скобок записываются с противоположными знаками.
Пример 1. Представить многочлен 3x 4 + 2x 3 + 5x 2 − 4 в виде суммы каких-нибудь двучленов:
Пример 2. Представить многочлен 3x 4 + 2x 3 + 5x 2 − 4 в виде разности каких-нибудь двучленов:
Перед вторыми скобками располагался минус, поэтому члены 5x 2 и −4 были записаны с противоположными знаками.
Многочлен и его стандартный вид
Многочлен, как и одночлен, можно привести к стандартному виду. В результате получается упрощенный многочлен, с которым удобно работать.
Чтобы привести многочлен к стандартному виду, нужно привести подобные слагаемые в этом многочлене. Подобные слагаемые в многочлене называют подобными членами многочлена, а приведение подобных слагаемых в многочлене — приведением его подобных членов.
Подобные члены многочлена это члены, имеющие одинаковую буквенную часть.
Приведём многочлен 2x + 4xy 2 + x − xy 2 к стандартному виду. Для этого приведём его подобные члены. Подобными членами в этом многочлене являются 2x и x , а также 4xy 2 и −xy 2 .
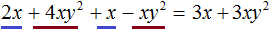
В результате получили многочлен 3x + 3xy 2 , который не имеет подобных членов. Такой вид многочлена называют многочленом стандартного вида.
Как и у одночлена, у многочлена имеется степень. Чтобы определить степень многочлена, сначала его нужно привести к стандартному виду, затем выбрать тот одночлен, степень которого является наибольшей из всех.
В предыдущем примере мы привели многочлен 2x + 4xy 2 + x − xy 2 к стандартному виду. В результате получили многочлен 3x + 3xy 2 . Он состоит из двух одночленов. Степенью первого одночлена является 1, а степенью второго одночлена является 3. Наибольшая из этих степеней является 3. Значит, многочлен 3x + 3xy 2 является многочленом третьей степени.
А поскольку многочлен 3x + 3xy 2 тождественно равен предыдущему многочлену 2x + 4xy 2 + x − xy 2 , то и этот предыдущий многочлен является многочленом третьей степени.
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в него одночленов.
В некоторых многочленах прежде всего требуется привести к стандартному виду одночлены, входящие в него, и только потом приводить сам многочлен к стандартному виду.
Например, приведем многочлен 3xx 4 + 3xx 3 − 5x 2 x 3 − 5x 2 x к стандартному виду. Этот многочлен состоит из одночленов, которые не приведены к стандартному виду. Сначала приведём их к стандартному виду:
Теперь получившийся многочлен 3x 5 + 3x 4 − 5x 5 − 5x 3 можно привести к стандартному виду. Для этого приведем его подобные члены. Подобными являются члены 3x 5 и −5x 5 . Больше подобных членов нет. Члены 3x 4 и −5x 3 будут переписаны без изменений:
Пример 2. Привести многочлен 3ab + 4cc + ab + 3c 2 к стандартному виду.
Сначала приведем одночлен 4cc , входящий в исходный многочлен, к стандартному виду, получим 4с 2
Далее приведём подобные члены:
Пример 3. Привести многочлен 4x 2 − 4y − x 2 + 17y − y к стандартному виду.
Подобными членами в данном многочлене являются 4x 2 и −x 2 , а также −4y , 17y и −y . Приведем их:
Приводя подобные члены, можно использовать скобки. Для этого подобные члены следует заключить в скобки, затем объединить выражения в скобках с помощью знака «плюс».
Решим предыдущий пример с помощью скобок. Подобными членами в нём были 4x 2 и −x 2 , а также −4y , 17y и −y . Заключим их в скобки и объединим с помощью знака «плюс»
Теперь в скобках выполним приведение подобных членов:
В получившемся выражении (3x 2 ) + (12y) раскроем скобки:
Конечно, такой подход нагромождает выражение, но зато позволяет свести к минимуму допущение ошибок.
Пример 4. Привести многочлен 12x 2 − 9y − 9x 2 + 6y + y к стандартному виду.
Заключим в скобки подобные слагаемые и объединим их с помощью знака «плюс»
Далее вычисляем содержимое скобок:
Избавляемся от скобок при помощи раскрытия:
Изменение порядка следования членов
Рассмотрим двучлен x − y . Как сделать так, чтобы член −y располагался первым, а член x вторым?
Многочлен это сумма одночленов. То есть исходный двучлен двучлен x − y является суммой x и −y
От перестановки мест слагаемых сумма не меняется. Тогда x и −y можно поменять местами
Пример 2. В двучлене −y − x поменять местами члены.
Двучлен −y − x это сумма членов −y и −x
Тогда согласно переместительному закону сложения получим (−x) + (−y) . Избавим выражение от скобок:
Таким образом, решение можно записать покороче:
Пример 3. Упорядочить члены многочлена x + xy 3 − x 2 в порядке убывания степеней.
Наибольшую степень в данном многочлене имеет член xy 3 , далее −x 2 , а затем x . Запишем их в этом порядке:
Умножение одночлена на многочлен
Одночлен можно умножить на многочлен. Чтобы умножить одночлен на многочлен, нужно этот одночлен умножить на каждый член многочлена и полученные произведения сложить.
Например, умножим одночлен 3x 2 на многочлен 2x + y + 5 . При умножении одночлена на многочлен, последний нужно заключать в скобки:
Теперь умножим одночлен 3x 2 на каждый член многочлена 2x + y + 5 . Получающиеся произведения будем складывать:
Вычислим получившиеся произведения:
Таким образом, при умножении одночлена 3x 2 на многочлен 2x + y + 5 получается многочлен 6x 3 + 3x 2 y + 15x 2 .
Умножение желательно выполнять в уме. Так решение получается короче:
В некоторых примерах одночлен располагается после многочлена. В этом случае опять же каждый член многочлена нужно перемножить с одночленом и полученные произведения сложить.
Например, предыдущий пример мог быть дан в следующем виде:
В этом случае мы умножили бы каждый член многочлен (2x + y + 5) на одночлен 3x 2 и сложили бы полученные результаты:
Умножение одночлена на многочлен (или умножение многочлена на одночлен) основано на распределительном законе умножения.
То есть чтобы умножить число a на сумму b + c , нужно число a умножить на каждое слагаемое суммы b + c , и полученные произведения сложить.
Вообще, умножение одночлена на многочлен, да и распределительный закон умножения имеют геометрический смысл.
Допустим, имеется прямоугольник со сторонами a и b

Увеличим сторону b на c

Достроим отсутствующую сторону и закрасим для наглядности получившийся прямоугольник:

Теперь вычислим площадь получившегося большого прямоугольника. Он включает в себя желтый и серый прямоугольники.
Чтобы вычислить площадь получившегося большого прямоугольника, можно по отдельности вычислить площади желтого и серого прямоугольников и сложить полученные результаты. Площадь желтого прямоугольника будет равна ab , а площадь серого ac
А это всё равно что длину большого прямоугольника умножить на его ширину. Длина в данном случае это b + c , а ширина это a
или ширину умножить на длину, чтобы расположить буквы a, b и c в алфавитном порядке:
Таким образом, выражения a × (b + c) и ab + ac равны одному и тому же значению (одной и той же площади)
К примеру, пусть у нас имеется прямоугольник длиной 4 см, и шириной 2 см, и мы увеличили длину на 2 см
Тогда площадь данного прямоугольника будет равна 2 × (4 + 2) или сумме площадей желтого и серого прямоугольников: 2 × 4 + 2 × 2 . Выражения 2 × (4 + 2) и 2 × 4 + 2 × 2 равны одному и тому же значению 12
2 × (4 + 2) = 2 × 4 + 2 × 2 = 12.
Действительно, в получившемся большом прямоугольнике содержится двенадцать квадратных сантиметров:
Пример 2. Умножить одночлен 2a на многочлен a 2 − 7a − 3
Умножим одночлен 2a на каждый член многочлена a 2 − 7a − 3 и сложим полученные произведения:
Пример 3. Умножить одночлен −a 2 b 2 на многочлен a 2 b 2 − a 2 − b 2
Умножим одночлен −a 2 b 2 на каждый член многочлена a 2 b 2 − a 2 − b 2 и сложим полученные произведения:
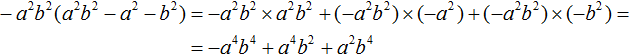
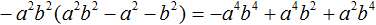
Пример 4. Выполнить умножение −1,4x 2 y 6 (5x 3 y − 1,5xy 2 − 2y 3 )
Умножим одночлен −1,4x 2 y 6 на каждый член многочлена 5x 3 y − 1,5xy 2 − 2y 3 и сложим полученные произведения:
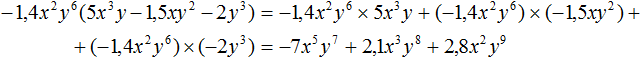
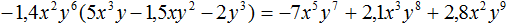
Пример 5. Выполнить умножение 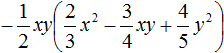
Умножим одночлен 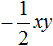 на каждый член многочлена
на каждый член многочлена 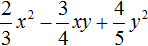 и сложим полученные произведения:
и сложим полученные произведения:

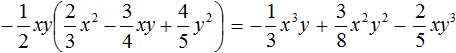
Выполняя короткие решения, результаты записывают сразу друг за другом вместе со знаком полученного члена. Рассмотрим поэтапно, как было выполнено короткое решение данного примера.
Сначала одночлен 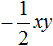 нужно умножить на первый член многочлена
нужно умножить на первый член многочлена 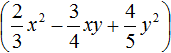 , то есть на
, то есть на 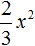 . Умножение выполняется в уме. Получается результат
. Умножение выполняется в уме. Получается результат 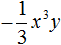 . В исходном выражении ставим знак равенства и записываем первый результат:
. В исходном выражении ставим знак равенства и записываем первый результат:
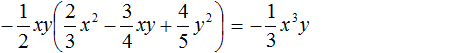
После этого в исходном выражении никаких знаков ставить нельзя. Нужно сразу приступать к следующему умножению.
Следующим шагом будет умножение одночлена 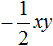 на второй член многочлена
на второй член многочлена 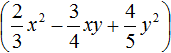 , то есть на
, то есть на 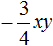 . Получается результат
. Получается результат 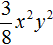 . Этот результат является положительным, то есть со знаком плюс
. Этот результат является положительным, то есть со знаком плюс 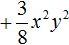 . В исходном выражении этот результат записывается вместе с этим плюсом сразу после члена
. В исходном выражении этот результат записывается вместе с этим плюсом сразу после члена 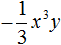
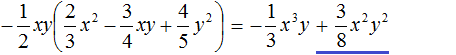
После этого в исходном выражении никаких знаков ставить нельзя. Нужно сразу приступать к следующему умножению.
Следующим шагом будет умножение одночлена 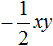 на третий член многочлена
на третий член многочлена 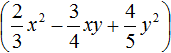 , то есть на
, то есть на 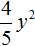 . Получается результат
. Получается результат 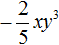 . Этот результат является отрицательным, то есть со знаком минус. В исходном выражении этот результат записывается вместе со своим минусом сразу после члена
. Этот результат является отрицательным, то есть со знаком минус. В исходном выражении этот результат записывается вместе со своим минусом сразу после члена 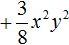
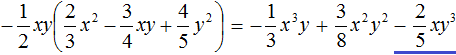
Иногда встречаются выражения, в которых сначала нужно выполнить умножение одночлена на многочлен, затем опять на одночлен. Например:
В этом примере сначала член 2 умножается на многочлен (a + b) , затем результат умножается на c . Для начала выполним умножение 2 на (a + b) и заключим полученный результат в скобки
Скобки говорят о том, что результат умножения 2 на (a + b) полностью умножается на c . Если бы мы не заключили скобки 2a + 2b , то получилось бы выражение 2a + 2b × с , в котором на с умножается только 2b . Это привело бы к изменению значения изначального выражения, а это недопустимо.
Итак, получили (2a + 2b)с . Теперь умножаем многочлен (2a + 2b) на одночлен c и получаем окончательный результат:
Умножение также можно было бы выполнить сначала умножив (a + b) на с и полученный результат перемножить с членом 2
В данном случае срабатывает сочетательный закон умножения, который говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий:
a × b × с = (a × b) × с = a × (b × с)
То есть умножение можно выполнять в любом порядке. Это не приведёт к изменению значения изначального выражения.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, нужно каждый член первого многочлена умножить на каждый член второго многочлена и полученные произведения сложить.
Например, умножим многочлен x + 3 на y + 4
Заключим в скобки каждый многочлен и объединим их знаком умножения ×
Либо запишем их друг за другом без знака × . Это тоже будет означать умножение:
Теперь умножим каждый член первого многочлена (x + 3) на каждый член второго многочлена (y + 4) . Здесь опять же будет применяться распределительный закон умножения:
Отличие в том, что у нас вместо переменной c имеется многочлен (y + 4) , состоящий из членов y и 4 . Наша задача умножить (x + 3) сначала на y , затем на 4. Чтобы не допустить ошибку, можно представить, что члена 4 пока не существует вовсе. Для этого его можно закрыть рукой:
Получаем привычное для нас умножение многочлена на одночлен. А именно, умножение многочлена (x + 3) на одночлен y . Выполним это умножение:
Мы умножили (x + 3) на y . Теперь осталось умножить (x + 3) на 4. Для этого умножаем каждый член многочлена (x + 3) на одночлен 4. На этот раз в исходном выражении (x + 3)(y + 4) рукой закроем y , поскольку на него мы уже умножали многочлен (x + 3)

Получаем умножение многочлена (x + 3) на одночлен 4. Выполним это умножение. Умножение необходимо продолжать в исходном примере (x + 3)(y + 4) = xy + 3y
Таким образом, при умножении многочлена (x + 3) на многочлен (y + 4) получается многочлен xy + 3y + 4x + 12.
По другому умножение многочлена на многочлен можно выполнить ещё так: каждый член первого многочлена умножить на второй многочлен целиком и полученные произведения сложить.
Решим предыдущий пример, воспользовавшись этим способом. Умножим каждый член многочлена x + 3 на весь многочлен y + 4 целиком и сложим полученные произведения:
В результате приходим к умножению одночлена на многочлен, которое мы изучили ранее. Выполним это умножение:
Получится тот же результат что и раньше, но члены полученного многочлена будут располагаться немного по другому.
Умножение многочлена на многочлен имеет геометрический смысл. Допустим, имеется прямоугольник, длина которого a и ширина b
Площадь этого прямоугольника будет равна a × b .
Увеличим длину данного прямоугольника на x , а ширину на y
Достроим отсутствующие стороны и закрасим для наглядности получившиеся прямоугольники:
Теперь вычислим площадь получившегося большого прямоугольника. Для этого вычислим по отдельности площадь каждого прямоугольника, входящего в этот большой прямоугольник и сложим полученные результаты. Площадь жёлтого прямоугольника будет равна ab , площадь серого xb , площадь фиолетового ay , площадь розового xy
А это всё равно что умножить длину получившегося большого прямоугольника на его ширину. Длина в данном случае это a + x , а ширина b + y
То есть выражения (a + x)(b + y) и ab + xb + ay + xy тождественно равны
Представим, что у нас имелся прямоугольник, длиной 6 см и шириной 3 см, и мы увеличили его длину на 2 см, а ширину на 1 см
Достроим отсутствующие стороны и закрасим для наглядности получившиеся прямоугольники:
Площадь получившегося большого прямоугольника будет равна (6 + 2)(3 + 1) или сумме площадей прямоугольников, входящих в большой прямоугольник: 6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 . В обоих случаях получим один и тот же результат 32
6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 32
(6 + 2)(3 + 1) = 6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 18 + 6 + 6 + 2 = 32
Действительно, в получившемся большом прямоугольнике содержится тридцать два квадратных сантиметра:
Пример 2. Умножить многочлен a + b на c + d
Заключим исходные многочлены в скобки и запишем их друг за другом:
Теперь умножим каждый член первого многочлена (a + b) на каждый член второго многочлена (c + d)
Пример 4. Выполнить умножение (−x − 2y)(x + 2y 2 )
Умножим каждый член многочлена (−x − 2y) на каждый член многочлена (x + 2y 2 )
Результат перемножения членов нужно записывать вместе со знаками этих членов. Рассмотрим поэтапно, как был решён данный пример.
Итак, требуется умножить многочлен (−x − 2y) на многочлен (x + 2y 2 ) . Сначала надо умножить многочлен (−x − 2y) на первый член многочлена (x + 2y 2 ) , то есть на x .
Умножаем −x на x , получаем −x 2 . В исходном выражении (−x − 2y)(x + 2y 2 ) ставим знак равенства и записываем −x 2
После этого в исходном выражении никаких знаков ставить нельзя. Нужно сразу приступать к следующему умножению. А именно умножению −2y на x . Получится −2xy . Этот результат является отрицательным, то есть со знаком минус. В исходном выражении записываем результат −2xy сразу после члена −x 2
Теперь умножаем многочлен (−x − 2y) на второй член многочлена (x + 2y 2 ) , то есть на 2y 2
Умножаем −x на 2y 2 , получаем −2xy 2 . В исходном выражении записываем этот результат сразу после члена −2xy
Приступаем к следующему умножению. А именно умножению −2y на 2y 2 . Получаем −4y 3 . В исходном выражении этот результат записываем вместе со своим минусом сразу после члена −2xy 2
Пример 5. Выполнить умножение (4a 2 + 2ab − b 2 )(2a − b)
Умножим каждый член многочлена (4a 2 + 2ab − b 2 ) на каждый член многочлена (2a − b)
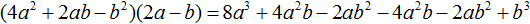
В получившемся выражении можно привести подобные слагаемые:
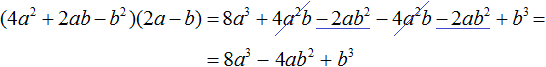
Пример 6. Выполнить умножение −(a + b)(с − d)
В этот раз перед скобками располагается минус. Этот минус является коэффициентом −1 . То есть исходное выражение является произведением трёх сомножителей: −1 , многочлена (a + b) и многочлена (с − d) .
Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то его можно вычислять в любом порядке.
Поэтому сначала можно перемножить многочлены (a + b) и (с − d) и полученный в результате многочлен умножить на −1 . Перемножение многочленов (a + b) и (с − d) нужно выполнять в скобках
Теперь перемножаем −1 и многочлен (ac + bc − ad − bd) . В результате все члены многочлена ( ac + bc − ad − bd ) поменяют свои знаки на противоположные:
Либо можно было перемножить −1 с первым многочленом (a + b) и результат перемножить с многочленом (с − d)
Пример 7. Выполнить умножение x 2 (x + 5)(x − 3)
Сначала перемножим многочлены (x + 5) и (x − 3) , затем полученный в результате многочлен перемножим с x 2
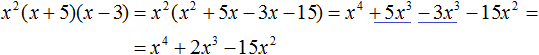
Пример 8. Выполнить умножение (a + 1)(a + 2)(a + 3)
Сначала перемножим многочлены (a + 1) и (a + 2) , затем полученный многочлен перемножим с многочленом (a + 3)
Итак, перемножим (a + 1) и (a + 2)
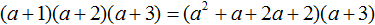
Полученный многочлен (a 2 + a + 2a + 2) перемножим с (a + 3)
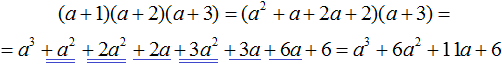
Если быстрое перемножение многочленов на первых порах даётся тяжело, можно воспользоваться подробным решением, суть которого заключается в том, чтобы записать, как каждый член первого многочлена умножается на весь второй многочлен целиком. Такая запись хоть и занимает место, но позволяет свести к минимуму допущение ошибок.
Например, выполним умножение (a + b)(c + d)
Запишем как каждый член многочлена a + b умножается на весь многочлен c + d целиком. В результате придём к умножению одночлена на многочлен, выполнять которое проще:
Такая запись удобна при умножении двучлена на какой-нибудь многочлен, в котором содержится больше двух членов. Например:
Или при перемножении многочленов, содержащих больше двух членов. Например, умножим многочлен x 2 + 2x − 5 на многочлен x 3 − x + 2
Запишем перемножение исходных многочленов в виде умножения каждого члена многочлена x 2 + 2x − 5 на многочлен x 3 − x + 2 .
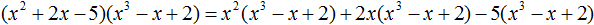
Получили привычное для нас умножения одночленов на многочлены. Выполним эти умножения:
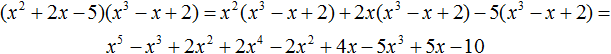
В получившемся многочлене приведём подобные члены:
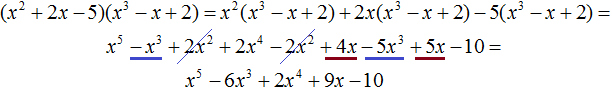
Одночлены, входящие в получившийся многочлен, расположим в порядке убывания степеней. Делать это необязательно. Но такая запись будет красивее:

Вынесение общего множителя за скобки
Мы уже учились выносить общий множитель за скобки в простых буквенных выражениях. Теперь мы немного углубимся в эту тему, и научимся выносить общий множитель за скобки в многочлене. Принцип вынесения будет таким же, как и в простом буквенном выражении. Небольшие трудности могут возникнуть лишь с многочленами, состоящими из степеней.
Рассмотрим простой двучлен 6xy + 3xz . Вынесем в нём общий множитель за скобки. В данном случае за скобки можно вынести общий множитель 3x . Напомним, что при вынесении общего множителя за скобки, каждое слагаемое исходного выражения надо разделить на этот общий множитель:
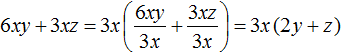
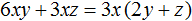
В результате получили 3x(2y + z) . При этом в скобках образовался другой более простой многочлен (2y + z) . Выносимый за скобки общий множитель выбирают так, чтобы в скобках остались члены, которые не содержат общего буквенного множителя, а модули коэффициентов этих членов не имели общего делителя, кроме единицы.
Поэтому в приведенном примере за скобки был вынесен общий множитель 3x . В скобках образовался многочлен 2y + z , модули коэффициентов которого не имеют общего делителя кроме единицы. Это требование можно выполнить, если найти наибольший общий делитель (НОД) модулей коэффициентов исходных членов. Этот НОД станóвится коэффициентом общего множителя, выносимого за скобки. В нашем случае исходный многочлен был 6xy + 3xz . Коэффициенты исходных членов это числа 6 и 3, а их НОД равен 3.
А буквенную часть общего множителя выбирают так, чтобы члены в скобках не имели общих буквенных множителей. В данном случае это требование выполнилось легко. Общий буквенный множитель был виден невооруженным глазом — это был множитель x .
Пример 2. Вынести общий множитель за скобки в многочлене x 2 + x + xy
Все члены данного многочлены имеют коэффициент единицу. Наибольший общий делитель модулей из этих единиц есть единица. Поэтому числовая часть выносимого за скобки множителя будет единицей. Но единицу в качестве коэффициента не записывают.
Далее выбираем буквенную часть общего множителя. Прежде всего надо понимать, что любой член, входящий в многочлен, является одночленом. А одночлен это произведение чисел, переменных и степеней. Даже если членом многочлена является обычное число, его всегда можно представить в виде произведения единицы и самого этого числа. Например, если в многочлене содержится число 5, его можно представить в виде 1 × 5 . Если в многочлене содержится число 8 , то его можно представить в виде произведения множителей 2 × 2 × 2 (или как 2 × 4 )
С переменными такая же ситуация. Если в многочлене содержится член, являющийся переменной или степенью, их всегда можно представить в виде произведения. К примеру, если многочлен содержит одночлен x , его можно представить в виде произведения 1 × x . Если же многочлен содержит одночлен x 3 , его можно представить в виде произведения xxx .
Одночлены, из которых состоит многочлен x 2 + x + xy , можно разложить на множители так, чтобы мы смогли увидеть буквенный сомножитель, который является общим для всех членов.
Итак, первый член многочлена x 2 + x + xy , а именно x 2 можно представить в виде произведения x × x . Второй член x можно представить в виде 1 × x . А третий член xy оставим без изменения, или для наглядности перепишем его с помощью знака умножения x × y
Каждый член многочлена представлен в виде произведения множителей, из которых состоят эти члены. Легко заметить, что во всех трёх произведениях общим сомножителем является x. Выделим его:
Этот множитель x и вынесем за скобки. Опять же при вынесении общего множителя за скобки каждое слагаемое исходного выражения делим на этот общий множитель. В нашем случае каждый член многочлена x × x + 1 × x + x × y нужно разделить на общий множитель x
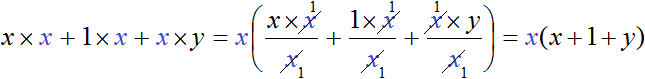
Значит, при вынесении общего множителя за скобки в многочлене x 2 + x + xy , получается x(x + 1 + y)
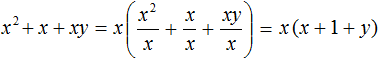
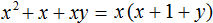
В результате в скобках остаются члены, которые не имеют общих буквенных сомножителей, а модули коэффициентов этих членов не имеют общих делителей, кроме 1.
Пример 2. Вынести общий множитель за скобки в многочлене 15x 2 y 3 + 12xy 2 + 3xy 2
Определим коэффициент общего множителя, выносимого за скобки. Наибольший общий делитель модулей коэффициентов 15, 12 и 3 это число 3. Значит, число 3 будет коэффициентом общего множителя, выносимого за скобки.
Теперь определим буквенную часть общего множителя, выносимого за скобки. Её нужно выбирать так, чтобы в скобках остались члены, которые не содержат общего буквенного множителя.
Перепишем буквенные части исходного многочлена 15x 2 y 3 + 12xy 2 + 3xy 2 в виде разложения на множители. Это позволит хорошо увидеть, что именно можно вынести за скобки:
Видим, что среди буквенных частей общим множителем является xyy , то есть xy 2 . Если вынести этот множитель за скобки, в скобках останется многочлен, не имеющий общего буквенного множителя.
В итоге общим множителем, выносимым за скобки, будет множитель 3xy 2
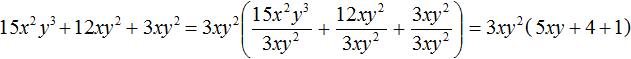
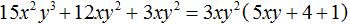
Для проверки можно выполнить умножение 3xy 2 (5xy + 4 + 1) . В результате должен получиться многочлен 15x 2 y 3 + 12xy 2 + 3xy 2
Пример 3. Вынести общий множитель за скобки в выражении x 2 + x
В данном случае за скобки можно вынести x
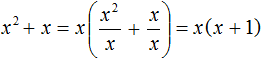
Это потому что первый член x 2 можно представить как xx . А второй член x представить как 1 × x
Не следует на письме подробно расписывать содержимое каждого члена, разлагая его на множители. Это легко делается в уме.
Пример 4. Вынести общий множитель за скобки в многочлене 5y 2 − 15y
В данном случае за скобки можно вынести 5y . Наибольший общий делитель модулей коэффициентов 5 и 15 это число 5. Среди буквенных множителей общим является y
Пример 5. Вынести общий множитель за скобки в многочлене 5y 2 − 15y 3
В данном примере за скобки можно вынести 5y 2 . Наибольший общий делитель модулей коэффициентов 5 и 15 это число 5 . Среди буквенных множителей общим является y 2
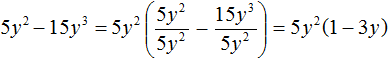
Пример 6. Вынести общий множитель за скобки в многочлене 20x 4 − 25x 2 y 2 − 10x 3
В данном примере за скобки можно вынести 5x 2 . Наибольший общий делитель модулей коэффициентов 20, −25 и −10 это число 5 . Среди буквенных множителей общим является x 2
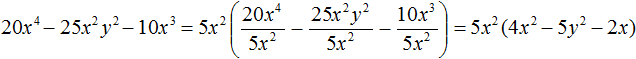
Пример 7. Вынести общий множитель за скобки в многочлене a m + a m + 1
Второй член a m + 1 представляет собой произведение из a m и a , поскольку a m × a = a m + 1
Заменим в исходном примере член a m + 1 на тождественно равное ему произведение a m × a . Так проще будет увидеть общий множитель:
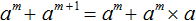
Теперь можно увидеть, что общим множителем является a m . Его и вынесем за скобки:
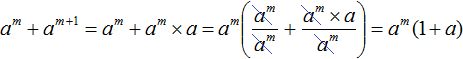
Проверка на тождественность
Решение задачи с многочленами порой растягивается на несколько строк. Каждое следующее преобразование должно быть тождественно равно предыдущему. Если возникают сомнения в правильности своих действий, то можно подставить произвольные значения переменных в исходное и полученное выражение. Если исходное и полученное выражение будут равны одному и тому же значению, то можно быть уверенным, что задача была решена правильно.
Допустим, нам нужно вынести общий множитель за скобки в следующем многочлене:
В данном случае за скобки можно вынести общий множитель 2x
Представим, что мы не уверены в таком решении. В этом случае нужно взять любое значение переменной x и подставить его сначала в исходное выражение 2x + 4x 2 , затем в полученное 2x(1 + 2x) . Если в обоих случаях результат будет одинаковым, то это будет означать, что задача решена правильно.
Возьмём произвольное значение x и подставим его в исходное выражение 2x + 4x 2 . Пусть x = 2 . Тогда получим:
2x + 4x 2 = 2 × 2 + 4 × 2 2 = 4 + 16 = 20
Теперь подставим значение 2 в преобразованное выражение 2x(1 + 2x)
2x(1 + 2x) = 2 × 2 × (1 + 2 × 2 ) = 4 × 5 = 20
То есть при x = 2 выражения 2x + 4x 2 и 2x(1 + 2x) равны одному и тому же значению. Это значит, что задача была решена правильно. Тоже самое будет происходить и при других значениях переменных x . Например, проверим наше решение при x = 1
2x + 4x 2 = 2 × 1 + 4 × 1 2 = 2 + 4 = 6
2x(1 + 2x) = 2 × 1 × (1 + 2 × 1 ) = 2 × 3 = 6
Пример 2. Вычесть из многочлена 5x 2 − 3x + 4 многочлен 4x 2 − x и проверить полученный результат, подставив вместо переменной x произвольное значение.
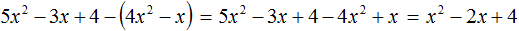
Мы выполнили два преобразования: cначала раскрыли скобки, а затем привели подобные члены. Теперь проверим эти два преобразования на тождественность. Пусть x = 2 . Подставим это значение сначала в исходное выражение, а затем в преобразованные:
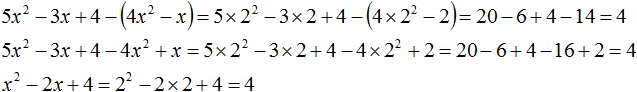
Видим, что при каждом преобразовании значение выражения при x = 2 не менялось. Это значит, что задача была решена правильно.
источники:
http://zftsh.online/articles/5013
http://spacemath.xyz/mnogochleny/
Найти сумму коэффициентов многочлена
Юлия
Профи
(963),
закрыт
13 лет назад
P(x)=(1-x)^7+(x^2-6x+9)^3(x^5+3x^4-2x^3+x^2+4x-7)^2+(x^2-3x+1)^3(x^3+5x+7)^2
Лучший ответ
Наталия Н
Профи
(921)
13 лет назад
Сумма коэффициентов многочлена равна значению многочлена при х=1
т. е. Р (1)=0+(1-6+9)^3(1+3-2+1+4-7)^2+(1-3+1)^3(1+5+7)^2=4^3*0^2+(-1)^3*13^2=0-169= -169
Остальные ответы
Николай
Гуру
(4971)
13 лет назад
Сумма коэффициентов многочлена – это его значение в точке 1, т. е. для нашего многочлена P(1)=0^7+4^3*0^2+(-1)^3*13^2=-169
Похожие вопросы
|
���������: 2+ ������: 8,9,10 |
�������� ����������� |
�������
������� ����� ���� ������������� ���������� (x² – 3x + 1)100 ����� ��������� ������ � ���������� �������� ������.
���������
����� ������������� ���������� ����� �������� ����� ���������� ��� x = 1.
�������
��� ����� ����� �������� ���������� ��� x = 1, �� ���� (1 – 3·1 + 1)100 = 1.
�����
1.
��������� � ���������� �������������
| web-���� |
| ������ |

§ 4. Некоторые приёмы решения алгебраических уравнений
Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени? Оказывается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.
Решите уравнение: `x^3 +4x^2 – 2x-3=0`.
Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:
`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`
$$ iff left[begin{array}{l}x-1=0,\ {x}^{2}+5x+3=0,end{array}right.iff left[begin{array}{l}x=1,\ x={displaystyle frac{-5pm sqrt{13}}{2}}.end{array}right.$$
`x=1`; `x=(-5+- sqrt13)/2`.
Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравнения? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.
Если несократимая дробь `p//q` (`p` – целое, `q` – натуральное) является корнем многочлена с целыми коэффициентами, то свободный член делится на `p`, а старший коэффициент делится на `q`.
Пусть несократимая дробь `p//q` – корень многочлена (8). Это означает, что
`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ …“+a_2 (p/q)^2 +a_1(p/q)+0=0`.
Умножим обе части на `q^n`, получаем:
`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + … + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.
Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:
`p(a_np^(n-1)+a_(n-1)p^(n-2)q+a_(n-2)p^(n-3)q^2+…+a_2pq^(n-2)+a_1q^(n-1))=-a_0q^n`. (14)
Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.
Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.
Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.
Решите уравнение
а) `x^4+4x^3-102x^2-644x-539=0`; (15)
б) `6x^4-35x^3+28x^2+51x+10=0`. (16)
а) Попробуем найти целые корни уравнения. Пусть `p` – корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:
`539=7^2*11`.
Поэтому `p` может принимать значения:
`+-1,+-7,+-11,+-49,+-77,+-539`.
Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:
`(x+1)(x^3+3x^2-105x-539)=0`.
Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:
`(x+1)(x+7)(x+7)(x-11)=0`.
`x=-7`; `x=-1`; `x=11`.
1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.
2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.
б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in{+-1;+-2;+-5;+-10}`; `qin{1;2;3;6}`.Возможные варианты для `x_0`:
`+-1,+-2,+-5,+-10,+-1/2,+-5/2,+-1/3,+-2/3,+-5/3,+-10/3,+-1/6,“+-5/6`.
Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем
`(2x-5)(3x^2-10x^2-11x-2)=0`.
Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` – корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:
`(2x-5)(3x+2)(x^2-4x-1)=0`.
Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.
`x=5/2`; `x=-2/3`; `x=2+-sqrt5`.
К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.
Разложите на множители:
а) `x^4+4`;
б)* `x^3-3x^2-3x-1`;
в) `x^4-x^3+2x^2-2x+4`;
г)* `x^4-4x^3-20x^2+13x-2`.
а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`
`=(x^2+2-2x)(x^2+2+2x)`.
Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:
`a^4+b^4=(a^2+b^2)^2-2a^2b^2=`
`=(a^2-sqrt2ab+b^2)(a^2+sqrt2ab+b^2)`.
б)* `x^3-3x^2-3x-1=2x^3-(x^3+3x^2+3x+1)`$$ ={left(sqrt[3]{2}xright)}^{3}-{left(x+1right)}^{3}=$$
$$ =left(sqrt[3]{2}x-x-1right)left(sqrt[3]{4}{x}^{2}+sqrt[3]{2}xleft(x+1right)+{left(x+1right)}^{2}right)$$.
в) Вынесем `x^2` за скобки и сгруппируем:
`x^4-x^3+2x^2-2x+4=x^2(x^2-x+2-2/x+4/x^2)=``x^2((x^2+4/x^2)-(x+2/x)+2)`.
Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:
`t^2-4-t+2=t^2-t-2=(t+1)(t-2)=(x+2/x+1)(x+2/x-2)`.
В итоге получаем:
`x^2(x+2/x+1)(x+2/x-2)=(x^2+2+x)(x^2+2-2x)=(x^2+x+2)(x^2-2x+2)`.
Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).
г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению
`x^2(x^2-2/x^2_(4x-13/x)-20)`.
Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.
Прибегнем к методу неопределённых коэффициентов. Пусть
`x^4-4x^3-20x^2+13x-2=(x^2+ax+b)(x^2+cx+d)`. (17)
Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:
`x^4-4x^3-20x^2+13x-2=`
`=x^4+(a+c)x^3+(b+ac+d)x^2+(ad+bc)x+bd`. (18)
Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:
$$ left{begin{array}{l}a+c=-4,\ b+ac+d=-20,\ ad+bc=13,\ bd=-2.end{array}right.$$ (19)
Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.
Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:
1) `b=1` и `d=-2`;
2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:
1) $$ left{begin{array}{l}a+c=-4,\ ac=-19,\ -2a+c=13.end{array}right.$$
Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.
2) $$ left{begin{array}{l}a+c=-4,\ ac=-21,\ -a+2c=13.end{array}right.$$
Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому
`x^4-4x^3-20+13x-2=(x^2-7x+2)(x^2+3x-1)`.
Далее каждый из квадратных трёхчленов можно разложить на множители.
Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.
Решите уравнение:
а) `(x-4)^2+|x-4|-2=0`;
б) `(x-7)^4+(x+1)^4=706`;
в) `1/(x^2+2x-3)+18/(x^2+2x+2)=18/((x+1)^2)`;
г) `(x-2)(x-4)(x+5)(x+7)=360`;
д) `(4x)/(4x^2-8x+7)+(3x)/(4x^2-10x+7)=1`;
е) `25x^4-150x^3+94x^2+150x+25=0`.
а) Обозначим `|x-4|=t`. Тогда `(x-4)^2=t^2` и получаем `t^2+t-2=0`, откуда $$ left[begin{array}{l}t=1,\ t=-2.end{array}right.$$
Если `t=-2`, то решений нет.
Если `t=1`, то `|x-4|=1 iff`$$ left[begin{array}{l}x=3,\ x=5.end{array}right.$$
`x=3`; `x=5`.
б) Обозначим `x-3=t`. Тогда получим
`(t-4)^4+(t+4)^4=706 iff(t^4-16t^3+96t^2-256t+256)+`
`+(t^4+16t^3+96t^2+256+256)=706 iff2t^4+192t^2-194=0iff`
`ifft^4+96t^2-97=0 iff(t^2-1)(t^2+97)=0 ifft=+-1`.
Значит, `x_1=4`, `x_2=2`.
`x=2`, `x=4`.
Уравнения вида `(x-a)^4+(x-b)^4=c` с помощью замены `x-((a+b))/2=t` сводятся к биквадратным.
в) Обозначим `x^2+2x+1=t`. Тогда `1/(t-4)+18/(t+1)=18/tiff`
$$ iff left{begin{array}{l}{t}^{2}+t+18left({t}^{2}-4tright)=18left({t}^{2}-3t-4right)\ tleft(t+1right)left(t-4right)ne 0end{array}right.iff $$
$$ iff left{begin{array}{l}{t}^{2}-17t+72=0,\ tleft(t+1right)left(t-4right)ne 0end{array}right.iff left[begin{array}{l}t=8,\ t=9.end{array}right.$$
Теперь найдём `x:`
$$ left[begin{array}{l}{left(x+1right)}^{2}=8,\ {left(x+1right)}^{2}=9end{array}right.iff left[begin{array}{l}x+1=pm 2sqrt{2},\ x+1=pm 3end{array}right.iff $$
$$ iff left[begin{array}{l}x=-1-2sqrt{2},\ x=-1+2sqrt{2},\ x=2,\ x=-4.end{array}right.$$
`x=-1+-2sqrt2`; `x=2`; `x=-4`.
г) Перемножим первую скобку с третьей, а вторую с четвёртой (убедитесь сами, что только такая группировка сомножителей помогает свести уравнение к квадратному).
`((x-2)(x+5))*((x-4)(x+7))=360iff`
`iff(x^2+3x-10)(x^2+3x-28)=360`.
Обозначим `x^2+3x-19=t`. Тогда уравнение принимает вид:
`(t+9)(t-9)=360ifft^2=441ifft=+-21`,
откуда
$$ left[begin{array}{l}{x}^{2}+3x-19=21,\ {x}^{2}+3x-19=-21end{array}right.iff left[begin{array}{l}{x}^{2}+3x-40=0,\ {x}^{2}+3x+2=0end{array}right.iff left[begin{array}{l}x=5,\ x=-8,\ x=-1,\ x=-2.end{array}right.$$
`x=-8`; `x=-2`; `x=-1`; `x=5`.
д) Разделим числитель и знаменатель каждой дроби на `x` (`x=0` не является решением уравнения):
`4/(4x-8+7/x)+3/(4x-10+7/x)=1`. Обозначим `4x+7/x-8=t`. Тогда
$$ {displaystyle frac{4}{t}}+{displaystyle frac{3}{t-2}}=1iff left{begin{array}{l}4left(t-2right)+3t={t}^{2}-2t,\ tleft(t-2right)ne 0end{array}right.iff $$
$$ iff left{begin{array}{l}{t}^{2}-9t+8=0,\ tleft(t-2right)ne 0end{array}right.iff left[begin{array}{l}t=1,\ t=8.end{array}right.$$
Теперь найдём `x:` $$ left[begin{array}{l}4x+{displaystyle frac{7}{x}}-8=1,\ 4x+{displaystyle frac{7}{x}}-8=8end{array}right.iff left[begin{array}{l}4{x}^{2}-9x+7=0,\ 4{x}^{2}-16x+7=0.end{array}right.$$
Уравнение `4x^2-9x+7=0` не имеет решений, а у уравнения `4x^2-16x+7=0` корнями являются числа `x=7/2` и `x=1/2`.
`x=1/2`; `x=7/2`.
е) `x!=0` (убеждаемся подстановкой), поэтому при делении обеих частей уравнения на `x^2` получим уравнение, равносильное исходному:
`25x^2-150x+94+150*1/x+25*1/x^2=0iff`
`iff(25x^2+25*1/x^2)-(150x-150*1/x)+94=0iff`
`iff25(x^2+1/x^2)-150(x-1/x)+94=0`.
Обозначим `x-1/x=t`. Тогда `t^2=(x-1/x)^2=x^2-2+1/x^2`, откуда `x^2+1/x^2=t^2+2`. Подставляем и решаем уравнение относительно `t:`
`25(t^2+2)-150t+94=0iff25t^2-150t+144=0iff5t^2-30t+144/5=0`.
Коэффициент при `t` чётный; по формуле четверти дискриминанта:
`D/4=15^2-5*(144)/5=225-144=81`; `t_1=(15+9)/5=24/5`; `t_2+(15-9)/5=6/5`.
Теперь найдём `x:`
$$ left[begin{array}{l}x-{displaystyle frac{1}{x}}={displaystyle frac{24}{5}},\ x-{displaystyle frac{1}{x}}={displaystyle frac{6}{5}}end{array}right.iff left[begin{array}{l}5{x}^{2}-24x-5=0,\ 5{x}^{2}-6x-5=0end{array}right.iff left[begin{array}{l}x=-{displaystyle frac{1}{5}};\ x=5;\ x={displaystyle frac{3pm sqrt{34}}{5}}.end{array}right.$$
`5`; `-1/5`; `(3+-sqrt(34))/5`.
1) Уравнения вида `ax^4+bx^3+cx^2+bx+a=0` называются возвратными. Для их решения делят обе части уравнения на `x^2` и вводят замену `x+-1/x=t`.
2) Некоторые другие уравнения четвёртой степени решаются с помощью замены `ax+b/x=t`. (См. пример 11в).
