На чтение 3 мин. Просмотров 10.8k.
Часто требуется найти сумму квадратов (x12+x22) или сумму кубов (x13+x23) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:
![]()
Помочь в этом может теорема Виета:
Сумма корней приведенного квадратного уравнения x2+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
x1+x2=-p; x1∙x2=q.
Выразим через p и q:
1) сумму квадратов корней уравнения x2+px+q=0;
2) сумму кубов корней уравнения x2+px+q=0.
Решение.
1) Выражение x12+x22 получится, если взвести в квадрат обе части равенства x1+x2=-p;
(x1+x2)2=(-p)2; раскрываем скобки: x12+2x1x2+ x22=p2; выражаем искомую сумму: x12+x22=p2-2x1x2=p2-2q. Мы получили полезное равенство: x12+x22=p2-2q.
2) Выражение x13+x23 представим по формуле суммы кубов в виде:
(x13+x23)=(x1+x2)(x12-x1x2+x22)=-p·(p2-2q-q)=-p·(p2-3q).
Еще одно полезное равенство: x13+x23=-p·(p2-3q).
Примеры.
3) x2-3x-4=0. Не решая уравнение, вычислите значение выражения x12+x22 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения
x1+x2=-p=3, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 1) равенство:
x12+x22=p2-2q. У нас -p=x1+x2=3 → p2=32=9; q=x1x2=-4. Тогда x12+x22=9-2·(-4)=9+8=17.
Ответ: x12+x22=17.
4) x2-2x-4=0. Вычислить: x13+x23.
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения x1+x2=-p=2, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 2) равенство: x13+x23=-p·(p2-3q)=2·(22-3·(-4))=2·(4+12)=2·16=32.
Ответ: x13+x23=32.
Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.
5) 2x2-5x-7=0. Не решая, вычислить: x12+x22.
Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x2-2,5x-3,5=0.
По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.
Решаем так же, как пример 3), используя равенство: x12+x22=p2-2q.
x12+x22=p2-2q=2,52-2∙(-3,5)=6,25+7=13,25.
Ответ: x12+x22=13,25.
6) x2-5x-2=0. Найти:
![]() Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x12+x22=p2-2q.
Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x12+x22=p2-2q.
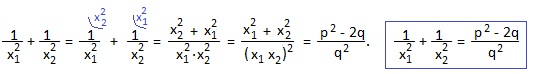
В нашем примере x1+x2=-p=5; x1∙x2=q=-2. Подставляем эти значения в полученную формулу:
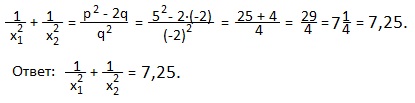
7) x2-13x+36=0. Найти:
![]() Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.
Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.
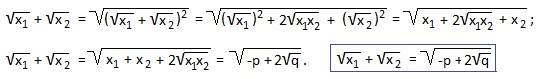
У нас x1+x2=-p=13; x1∙x2=q=36. Подставляем эти значения в выведенную формулу:
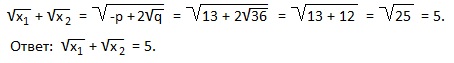
Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!
- Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
- Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax 2 + c = 0, при b = 0;
- ax 2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax 2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.
Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x 2 = 0.
- Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
Как решить уравнение ax 2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
- перенесем c в правую часть: ax 2 = – c,
- разделим обе части на a: x 2 = – c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а 2 = – c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = – c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = – c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = – c/а. Ура, больше у этого уравнения нет корней.
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:
- не имеет корней при — c/а 0.
| В двух словах |
|---|
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
-
Перенесем свободный член в правую часть:
Разделим обе части на 8:
Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.
Как решить уравнение ax 2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0
0,5x = 0,125,
х = 0,125/0,5
Ответ: х = 0 и х = 0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2).
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b 2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b 2 −4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
- Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x 2 = 0.
-
Произведем равносильные преобразования. Умножим обе части на −1
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x 2 — х = 0.
-
Преобразуем уравнение так, чтобы появились множители
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x 2 — 10 = 39.
-
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
-
Найдем дискриминант по формуле
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.
Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 – 4ac = 4n 2 — 4ac = 4(n 2 – ac) и подставим в формулу корней:
2 + 2nx + c = 0″ height=”705″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png” width=”588″>
Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n 2 – ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n 2 – ac;
- если D1 0, значит можно найти два действительных корня по формуле
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=”215″ src=”https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE” width=”393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=”52″ src=”https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG” width=”125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=”52″ src=”https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo” width=”112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
-
Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=”59″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png” width=”117″>
Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x 2 – 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 – 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 – 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
[spoiler title=”источники:”]
http://www.sites.google.com/site/kvadratnyeuravenia/information/teorema-vieta
http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya
[/spoiler]
Квадратные уравнения с параметром
Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.
Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!
Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:
— Что такое квадратное уравнение, как оно выглядит и как решается?
— Что такое дискриминант и куда его пристроить?
— Что такое теорема Виета и где её можно применить?
Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.
Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂
Пример 1
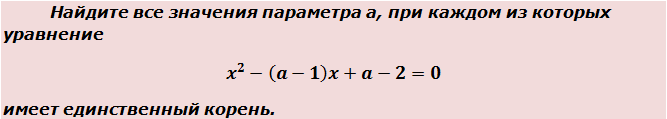
Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:
Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.
Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!
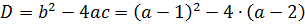
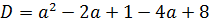
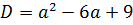
Теперь надо приравнять наш дискриминант к нулю:
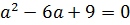
Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3) 2 !
Респект внимательным! Верно! Если заменить наше выражение слева на (a-3) 2 , то уравнение будет решаться в уме!
Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)
Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.
Пример 2
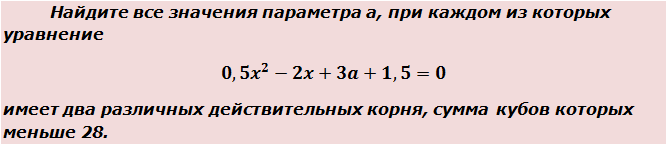
Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:
0,5x 2 — 2x + 3a + 1,5 = 0
Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:
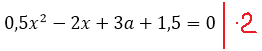
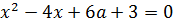
Выписываем в столбик наши коэффициенты a, b, c:
Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!
А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:
«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»
Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:
Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.
Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:
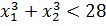
Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:
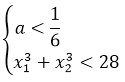
А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.
Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:
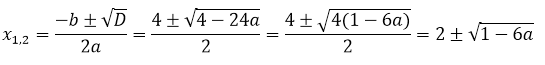
Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:
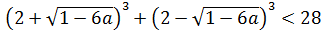
А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.
Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:
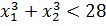
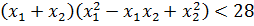
А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:
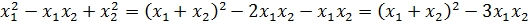
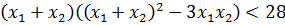
Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:
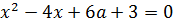
Чему здесь равен коэффициент при x 2 ? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:
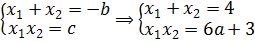
Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:
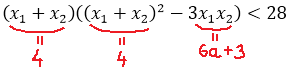
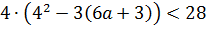
Осталось раскрыть скобки и решить простенькое линейное неравенство:
Вспоминаем, что ещё у нас есть глобальное требование a 0 необходимо пересечь с условием a . Рисуем картинку, пересекаем, и записываем окончательный ответ.
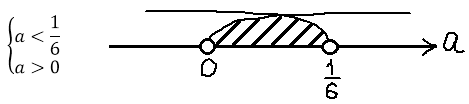
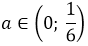
Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!
Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.
Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.
Например, такая задачка из реального варианта ЕГЭ:
Пример 3
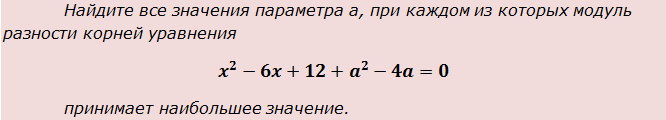
Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»
Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:
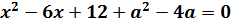
А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:
Что ж, аккуратно расписываем наш дискриминант через параметр а:
А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:
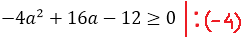
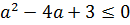
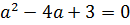
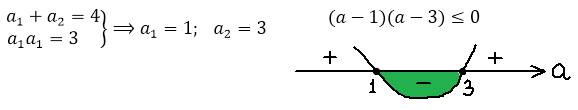
Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)
А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука
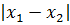
принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x1 — x2. Теорема Виета здесь в этот раз бессильна.
Что ж, считаем корни по общей формуле:
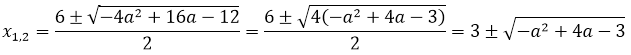
Дальше составляем модуль разности этих самых корней:
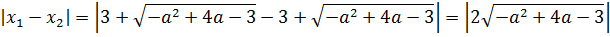
Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:
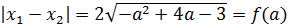
И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)
Дифференцируем нашу функцию и приравниваем производную к нулю:
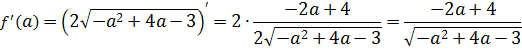
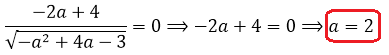
Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).
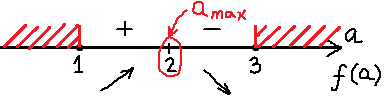
Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.
Всё. Вот теперь наша задача полностью решена.
Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).
Пример 4
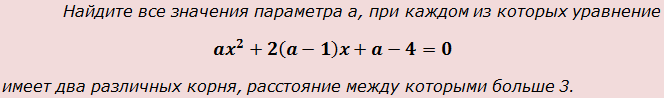
Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?
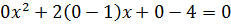
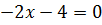
Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)
При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.
А далее по накатанной колее. Считаем дискриминант:
D = 4(a-1) 2 — 4a(a-4) = 4a 2 -8a+4-4a 2 +16a = 4+8a
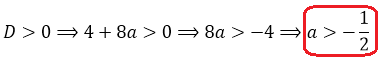
Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.
Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:
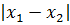
Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.
Значит, ответом на вопрос задачи является решение вот такой системы:
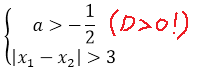
Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:
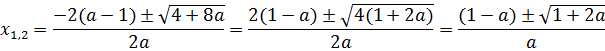
Отлично. Корни получены. Теперь начинаем формировать наше расстояние:
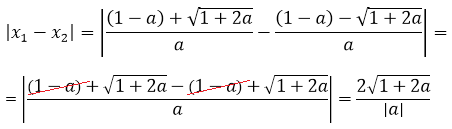
Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:
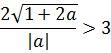
Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.
Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:
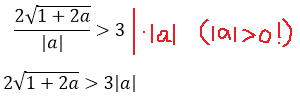
Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.
Случай 1 (a>0, |a|=a)
В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:
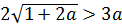
Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:
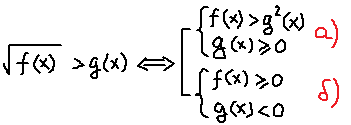
Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.
Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:
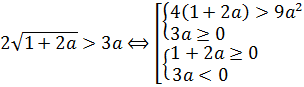
А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a 0 и a
Упрощаем нашу совокупность с учётом главного условия a>0:
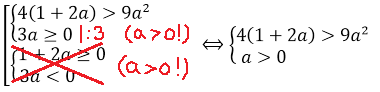
Вот так. А теперь решаем самое обычное квадратное неравенство:
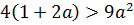
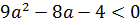
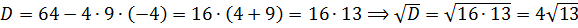
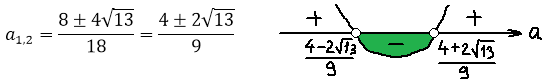
Нас интересует промежуток между корнями. Стало быть,
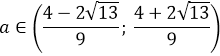
Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:
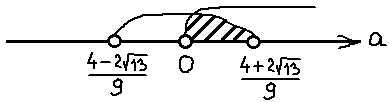
Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:
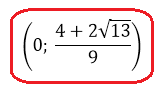
Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.
Случай 2 (a
В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:
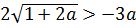
Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):
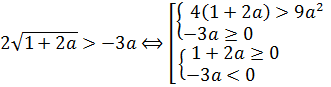
С учётом общего требования a
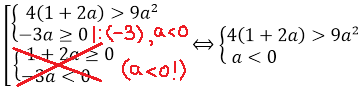
А дальше снова решаем обычное квадратное неравенство:
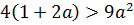
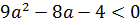
И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:
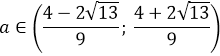
Осталось лишь пересечь этот интервал с нашим новым условием a
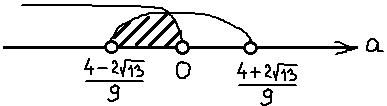
Вот и второй кусочек ответа готов:
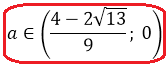
Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число
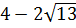
с нулём. Вот так:
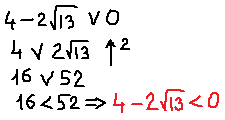
А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):
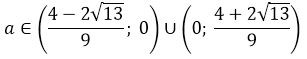
Готово дело. Эти два интервала — это пока ещё только решение неравенства
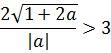
Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!
Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:
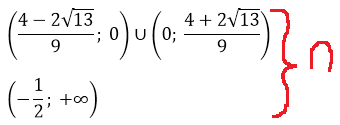
Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:
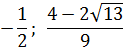
Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:
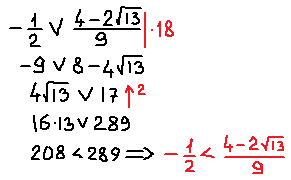
Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая:
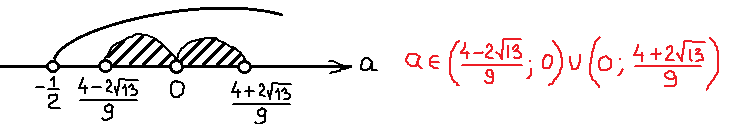
Всё, задача полностью решена и можно записывать окончательный ответ.
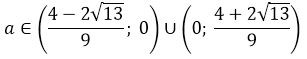
Ну как? Уловили суть? Тогда решаем самостоятельно.)
1. Найдите все значения параметра b, при которых уравнение
ax 2 + 3x +5 = 0
имеет единственный корень.
2. Найдите все значения параметра а, при каждом из которых больший корень уравнения
x 2 — (14a-9)x + 49a 2 — 63a + 20 = 0
3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения
x 2 — 4ax + 5a = 0
4. Найдите все значения параметра а, при каждом из которых уравнение
x 2 + 2(a-2)x + a + 3 = 0
имеет два различных корня, расстояние между которыми больше 3.
8.2.4. Применение теоремы Виета
Часто требуется найти сумму квадратов (x1 2 +x2 2 ) или сумму кубов (x1 3 +x2 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:
Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Выразим через p и q:
1) сумму квадратов корней уравнения x 2 +px+q=0;
2) сумму кубов корней уравнения x 2 +px+q=0.
Решение.
1) Выражение x1 2 +x2 2 получится, если взвести в квадрат обе части равенства x1+x2=-p;
(x1+x2) 2 =(-p) 2 ; раскрываем скобки: x1 2 +2x1x2+ x2 2 =p 2 ; выражаем искомую сумму: x1 2 +x2 2 =p 2 -2x1x2=p 2 -2q. Мы получили полезное равенство: x1 2 +x2 2 =p 2 -2q.
2) Выражение x1 3 +x2 3 представим по формуле суммы кубов в виде:
Еще одно полезное равенство: x1 3 +x2 3 =-p·(p 2 -3q).
Примеры.
3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x1 2 +x2 2 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения
x1+x2=-p=3, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 1) равенство:
x1 2 +x2 2 =p 2 -2q. У нас -p=x1+x2=3 → p 2 =3 2 =9; q=x1x2=-4. Тогда x1 2 +x2 2 =9-2·(-4)=9+8=17.
4) x 2 -2x-4=0. Вычислить: x1 3 +x2 3 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения x1+x2=-p=2, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 2) равенство: x1 3 +x2 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.
Ответ: x1 3 +x2 3 =32.
Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.
5) 2x 2 -5x-7=0. Не решая, вычислить: x1 2 +x2 2 .
Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.
По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.
Решаем так же, как пример 3), используя равенство: x1 2 +x2 2 =p 2 -2q.
x1 2 +x2 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.
Ответ: x1 2 +x2 2 =13,25.
6) x 2 -5x-2=0. Найти:
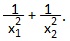 Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x1 2 +x2 2 =p 2 -2q.
Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x1 2 +x2 2 =p 2 -2q.
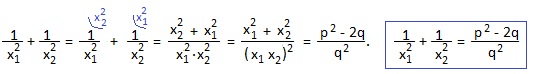
В нашем примере x1+x2=-p=5; x1∙x2=q=-2. Подставляем эти значения в полученную формулу:
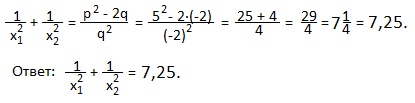
7) x 2 -13x+36=0. Найти:
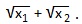 Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.
Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.
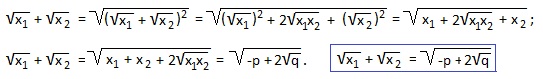
У нас x1+x2=-p=13; x1∙x2=q=36. Подставляем эти значения в выведенную формулу:
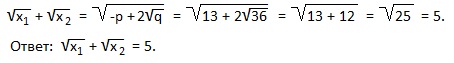
Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!
Как решать квадратные уравнения

О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней. Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: источники: http://mathematics-repetition.com/8-2-4-primenenie-teorem-vieta/ http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya |
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
Помогите решить задание по школьной алгебре. Сумма кубов корней квадратного уравнения [math]x^2+3x-2=0[/math] равна? По ответам должно получится -45 !
|
||
| Вернуться к началу |
|
||
|
Olavforever |
Заголовок сообщения: Re: уравнение
|
|
[math]x^2+3x-2=0[/math] нам необходимо найти сумму кубов [math](x_1+x_2)((x_1+x_2)^2-3x_1 cdot x_2)[/math] получаем -45
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Olavforever “Спасибо” сказали: pewpimkin |
|
|
brest-rap2011 |
Заголовок сообщения: Re: уравнение
|
|
Olavforever писал(а): [math]x^2+3x-2=0[/math] я пробывал подтавлять значения в формулу, но у меня получается не -45!
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Чему равна сумма модулей?
в форуме Алгебра |
Ivanko |
5 |
715 |
21 янв 2015, 16:18 |
|
Чему равна сумма делимого и делителя?
в форуме Алгебра |
oksi |
1 |
574 |
24 ноя 2014, 20:35 |
|
Сумма арифметических корней , корней квадратного уравнения
в форуме Алгебра |
TsaAst |
24 |
270 |
25 июн 2022, 10:30 |
|
Сумма двух чисел и сумма их квадратов равна четвертая степен
в форуме Теория чисел |
Phenol |
1 |
280 |
01 апр 2020, 14:23 |
|
Сумма двух чисел и сумма их квадратов равна кубу
в форуме Теория чисел |
johnson |
5 |
897 |
14 мар 2017, 22:00 |
|
Чему равна мощность
в форуме Механика |
Mazytta56 |
13 |
922 |
22 авг 2018, 23:21 |
|
Чему равна вероятность
в форуме Математическая статистика и Эконометрика |
andrey546 |
9 |
893 |
22 фев 2014, 15:59 |
|
Чему равна энергия
в форуме Электричество и Магнетизм |
_Help_ |
1 |
230 |
21 фев 2022, 20:59 |
|
Сумма трех кубов
в форуме Интересные задачи участников форума MHP |
bimol |
13 |
34652 |
31 мар 2019, 16:53 |
|
Опять сумма кубов
в форуме Алгебра |
alekscooper |
6 |
447 |
19 янв 2018, 07:09 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Теорема Виета в квадратных уравнениях — штука простая и очень-очень важная. Позволяет делать массу полезных вещей буквально в уме. Имеет смысл познакомиться и освоить, правда? Тем более это совсем просто. Сомневаетесь? Напрасно.) Сами увидите. Читаем дальше.
Что такое приведённое квадратное уравнение? Складываем и перемножаем корни…
Знакомство наше начнём с безобидного уравнения:
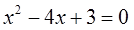
Обычное квадратное уравнение, ничего выдающегося. Коэффициенты a, b и c здесь следующие:
a = 1; b = -4; c = 3
Решаем тоже как обычно, безо всяких фокусов, через дискриминант и получаем два корня:
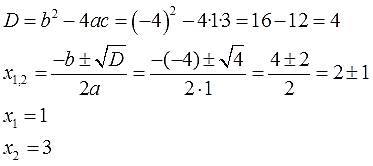
Уравнение как уравнение – и что с того? Ничего, сейчас интересно будет!)
Первым делом я возьму корни нашего уравнения и… сложу их.) Зачем? Так надо!
Итак:
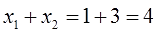
Теперь проделаю ещё одну бесполезную (казалось бы!) штуку. Перемножу корни:
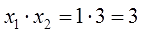
Ну сложил, ну перемножил — и что? Спокойствие и терпение!
Выпишем ещё разок само уравнение, а прямо под ним напишем сумму и произведение корней:
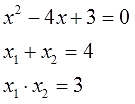
И посмотрим на нашу запись. Внимательно посмотрим… Ничего не бросается в глаза? Ведь многие важные открытия в математике совершались на основе хорошей наблюдательности, между прочим! Не видите…
А вот так?)
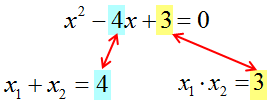
Да! Сумма корней нашего квадратного уравнения равна коэффициенту b. Но, обратите внимание, не просто b, а с противоположным знаком! В уравнении коэффициент при икс (а это и есть буковка b) равен минус четыре. Сумма же корней даёт плюс четыре. То есть, –b.
А произведение корней даёт нам свободный член! Т.е. буковку c. Даёт со своим знаком! Как была в уравнении тройка (с=3), так в произведении корней тройкой же и осталась.)
Теперь я немного изменю уравнение. Поменяю в нём свободный член с тройки на четвёрку. Вот такое уравнение теперь решим:
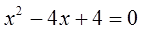
Решаем точно так же, через дискриминант (здесь он равен нулю), и получаем единственное решение x=2.
Но мы с вами люди уже достаточно взрослые и понимаем, что это не один корень, а два одинаковых:
x1,2 = 2
Поэтому снова сосчитаем сумму и произведение корней:
И опять в сумме мы получили –b (-b=+4), а в произведении с (c=+4)!
А вот это уже крайне важно! Оказывается, такая забавная штука будет получаться всегда для любого квадратного уравнения! Если оно имеет корни, разумеется.) Правда, уравнения не какого попало, а такого, где квадрат икса чистый (т.е. коэффициент a=1). В математике такие квадратные уравнения имеют своё особое название — приведённые квадратные уравнения.
Запоминаем:
Квадратное уравнение, в котором коэффициент при х2 равен единице (а=1), называется приведённым квадратным уравнением. Весьма важная штука!
Как оно выглядит в общем виде? Очень просто. Подставим в общий вид квадратного уравнения
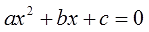
единичку вместо а и получим общий вид приведённого квадратного уравнения:
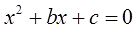
В некоторых учебниках коэффициенты b и с переобозначают другими буквами (чаще всего p и q) и получают вот такой общий вид
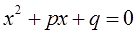
Но суть та же самая. Как говорится, хоть горшком назови… Лично я предпочитаю использовать традиционные буквы b и с. Для универсальности.)
Ну и что из этого? – спросите вы. Чем приведённые квадратные уравнения так выделяются на фоне остальных квадратных, неприведённых? А дело вот в чём.
Что такое теорема Виета?
Итак, мы выяснили, что в приведённом квадратном уравнении (любом!) сумма коэффициентов равна –b, а произведение равно с. Всегда. Ясное дело, если дискриминант неотрицательный и корни у уравнения имеются.
Математически эта фишка записывается вот так:
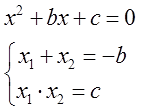
Этот любопытный факт — и есть теорема Виета! Собственной персоной.
А словами она звучит вот как:
Теорема Виета:
Если ПРИВЕДЁННОЕ квадратное уравнение имеет корни, то их сумма равна коэффициенту при икс, взятому с противоположным знаком (–b), а их произведение равно свободному члену (c).
Вот и всё, никаких премудростей.)
Хотите строгое доказательство? Пожалуйста! Флаг вам в руки!) Распишите общую формулу корней квадратного уравнения для a=1, составьте сумму и произведение корней в общем виде. Т.е. через буквы. И упростите. Попробуйте! Весьма полезно и познавательно, между прочим.)
Верна также и обратная теорема:
Если числа х1 и х2 таковы, что их сумма равна –b, а произведение равно c, то эти числа являются корнями приведённого квадратного уравнения x2 + bx + c = 0.
А по секрету скажу вам, что, на самом деле, именно обратной теоремой вы и пользуетесь, так умело подбирая в уме корни уравнения по сумме и произведению! Об этом подборе как раз дальше будет.)
Зачем нужна теорема Виета?
Полезная вещь первая — подбираем корни в уме!
Теорема Виета (обратная форма) позволяет искать корни многих квадратных уравнений гораздо быстрее и проще, чем традиционным путём через дискриминант. В буквальном смысле устно!
Вернёмся к нашему уравнению:
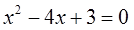
Теперь, вооружившись глубокими познаниями, прямо по теореме Виета, записываем системку для наших искомых корней:
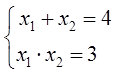
Вопрос на сообразительность: какие же такие два числа в сумме дают четвёрку, а в произведении — тройку? Немного подумав головой, можно довольно быстро догадаться, что это чиселки 1 и 3.
Значит, можно смело записать:
x1 = 1
x2 = 3
Вот и всё. Это и будут корни нашего уравнения. Оба подходят.) Здорово, правда? И не нужно считать никаких дискриминантов, возиться с общей формулой корней. В которой, между прочим, можно и ошибок наляпать… Сразу, в уме, получен верный ответ!
Возможно, кто-то уже приготовил мне вопрос. Очень грамотный вопрос, кстати. А всегда ли в случае приведённого квадратного уравнения можно вот так красиво и легко подобрать корни?
К сожалению, нет. Далеко не всегда. Например, я снова изменю в исходном уравнении свободный член, только вместо четвёрки напишу двойку. Вот такое уравнение пусть будет:
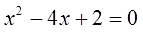
Уравнение приведённое, коэффициент а равен единичке, вроде бы, всё нормально. Пишем теорему Виета:
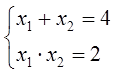
И снова пробуем подобрать иксы так, чтобы оба равенства сработали!
Гм… Что-то не подбирается, правда? Какие бы целые числа вы бы ни подбирали, ничего не выйдет.
Тут выход только один — решать через дискриминант. Ибо дискриминант — штука универсальная. Спасает всегда — и в приведённых уравнениях, и в обычных. Попробуйте. И вы убедитесь, что корни этого уравнения получаются иррациональными. Естественно, такие корни подобрать в уме несколько затруднительно, да…
Догадываюсь, что вы сейчас спросите: Зачем же нам тогда городить огород, пробовать подобрать корни, если дискриминант всё равно надёжнее и с ним-то уж точно всё решится?
Да, надёжнее, но… Не всё так просто, как кажется!
Дело всё в том, что квадратные уравнения изучаются в 8-м классе, где народ тренируется на простых (иногда — совсем примитивных) задачках. И… привыкает к простоте.) Затем, в старших классах и особенно в институте, при изучении высшей математики, квадратные уравнения представляются как нечто само собой разумеющееся. Но при этом в коэффициентах зачастую возникают такие большие числа, что работать с ними большинство учеников… просто не готовы!
Попадётся вам, к примеру, такая задачка:
Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 82 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 3 часа 25 минут позже автомобилиста. Ответ дайте в км/ч.
Это не моя разыгравшаяся фантазия, а вполне реальная задачка из ЕГЭ, между прочим.)
Кто в курсе, как решать текстовые задачи на движение, тот без труда составит вот такое уравнение:
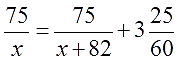
Классическое дробно-рациональное уравнение. Здесь х — скорость велосипедиста. Немного повозившись с ним (избавившись от дробей и упростив всё до упора), получим вот такое квадратное уравнение:
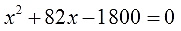
Если начать решать это уравнение по-рабочекрестьянски, то получим, что дискриминант у него равен аж 13924! И… что? Как нам из такого здоровенного числа корень извлекать? Без калькулятора! Слабо? То-то…
Зато через теорему Виета это злое уравнение решается практически устно! Не верите? Что ж, смотрите сами…
Записываем сумму и произведение корней:
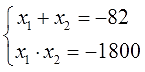
Осталось лишь догадаться, какие же числа дают в сумме минус 82, а в произведении минус 1800. Совсем чуточку подумав, довольно быстро получим, что:
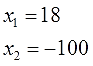
Минус сто, ясное дело, нас не интересует (скорость не бывает отрицательной), а вот 18 км/ч — вполне себе правдоподобная велосипедная скорость.)
Вот и все дела.) И без долгих и утомительных вычислений, связанных с извлечением корня из пятизначного числа! Здорово, правда?
Посему, первые практические советы:
1. Если перед вами квадратное уравнение приведённого вида, то первым делом пробуем найти корни подбором. По теореме, ОБРАТНОЙ теореме Виета. В подавляющем большинстве заданий это срабатывает.
2. Не боимся уравнений с большими коэффициентами! Самое главное — не бросаемся считать дискриминант! Как правило, корни таких уравнений также довольно легко ищутся подбором.
Может, конечно, и не повезти, но зачем же такой шанс упускать, правда?)
Но есть у меня для вас хорошая новость.) Составители большинства заданий — люди гуманные.) И стараются составить уравнение так, чтобы корни являлись целыми числами и их легко можно было бы подобрать. Пробуем делать это!
Переходим к следующей полезной вещи.
Полезная вещь вторая — проверяем корни!
Теорему Виета можно применять не только для подбора корней, но и для проверки корней, найденных другим способом (через дискриминант, например). Решили уравнение – проверьте сумму и произведение корней! Всё срослось — значит, верно. Нет — значит, где-то накосячили. Ищите ошибку.)
Например, такое уравнение:
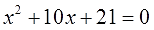
Дело нехитрое. Решаем себе через дискриминант, всё чин-чином, получаем корни:
x1 = -7
x2 = -3
Не бросаемся сразу же радостно писать ответ! Знаете поговорку доверяй, но проверяй?) Вот и не ленимся. Первым делом сложим наши корни:
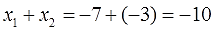
Получили -10. Обратите внимание, не десять, а минус десять! Коэффициент b с противоположным знаком. Так уж теорема Виета устроена.)
Последняя (и окончательная) проверка — перемножим корни. Должен получиться свободный член:
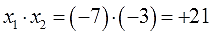
Вот теперь всё хорошо.)
Более того, с этой благородной целью (проверка корней) теорему Виета можно применять и для неприведённых квадратных уравнений. Для любых. Да-да, я не шучу! Но эту фишку я оставлю на конец урока. На десерт.)
И что, думаете, только для подбора и проверки корней теорема Виета и нужна? Вовсе нет!
Полезная вещь третья — когда корни считать… не надо!
Вы спросите, а разве можно обойтись и вовсе без вычисления корней? Можно! Ещё как!)
Дискриминант — штука, безусловно, удобная, простая и понятная. С ним, как правило, всё легко и предсказуемо. Но… Может получиться какой-нибудь дурацкий дискриминант: 17 там, скажем, или 20. Что неизбежно приводит к появлению иррациональных корней, да…) А уж если в задании надо ещё что-то делать с корнями, то выражения с радикалами, даже для опытного ученика, могут перерасти в большую проблему. А для неопытного — вообще превратиться в полный ахтунг.
Но теорема Виета иногда способна на настоящие чудеса!
Например, такое задание:
Дано квадратное уравнение:
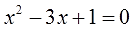
Найдите сумму квадратов корней, не находя самих корней.
Если сейчас начать решать это задание “в лоб” — считать дискриминант и искать корни уравнения по общей формуле, то получим вот таких двух красавцев:
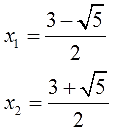
Нам нужна сумма их квадратов. И что нам теперь с такими лохматыми числами делать?! Возводить в квадрат, складывать… Нет, возвести и сложить можно, конечно, но… не каждый ученик дорешает до конца это задание без ошибок!
Не отчаиваемся и читаем ещё раз условие. Обратите внимание, нам вообще НЕ сказано “решать уравнение”, НЕ сказано “находить корни”. Более того, нам прямым текстом говорится: “Найти сумму квадратов корней, не находя самих корней“.
Что делать? Как выкручиваться без поиска корней?
Посмотрим ещё раз на уравнение. Приведённое, между прочим.) Раз так, то, стало быть, для него справедлива теорема Виета!
Можно смело записать:
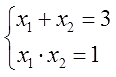
Вот так. Сумма корней — тройка, а произведение — единичка. Мы не знаем, чему равны сами эти корни, но у нас это и не спрашивают. Нас просят найти только сумму их квадратов.)
А вот теперь ключевой вопрос: А можно ли как-то расписать нужную нам сумму квадратов корней через сумму и произведение корней?
Да, можно! Кто на “ты” с формулами сокращённого умножения (а именно — с формулой квадрата суммы), тот, скорее всего, даже не заметит проблем.
Пишем:
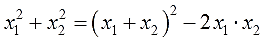
Как я додумался до этого равенства? Очень просто. Вспомнил, что в формуле квадрата суммы сидят сумма квадратов и удвоенное произведение:
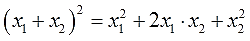
И выразил нужную величину (сумму квадратов) через остальные — сумму (т.е. квадрат суммы) и произведение (удвоенное).
Вот и всё, практически. Осталось лишь подставить тройку вместо суммы и единицу вместо произведения корней, да и посчитать, что получится:
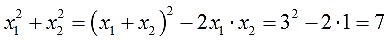
Ответ: 7
И все дела.) И корни не понадобились! Вообще.) Мощная штука — теорема Виета! Ну и формулы сокращённого умножения, само собой.)
Этот приём — выражение какой-то сложной конструкции через сумму и произведение корней — очень популярен в заданиях на теорему Виета! Я уж молчу про более серьёзные задания. Например, задачи с параметрами, там этот финт ушами используется на полную катушку.)
Запоминаем:
В серьёзных заданиях на сумму и произведение корней пользуемся формулами сокращённого умножения и алгеброй 7-го класса! Здорово помогает.)
Как работать с неприведёнными уравнениями?
Как известно, самое сладкое — в конце трапезы. Обещанный десерт.)
Во всех примерах этого урока мы работали лишь с приведёнными квадратными уравнениями. Такими, у которых коэффициент при квадрате икса — единичка. А если уравнение не является приведённым? Т.е. а≠1? Что тогда? Про теорему Виета можно забыть?
Нет, забывать мы не будем. Мы поступим мудро и красиво. Раз уравнение не является приведённым, то мы его… сделаем! Как? Очень просто! Берём квадратное уравнение в общем виде:
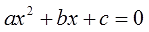
и… делим обе части на “а”! Очищаем квадрат икса от коэффициента. Можно ли так делать? Конечно! Мы ведь с вами уже в курсе, что a никогда не бывает равно нулю (а≠0). Иначе уравнение будет не квадратным, а линейным. Вот и делим смело. Это совершенно безопасно. Естественно, все остальные слагаемые тоже придётся поделить на а, от этого никак не отвертишься.
Получим:
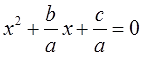
Вот и всё. Уравнение стало приведённым. Коэффициенты, правда, дробными стали, но тут уж ничего не поделать, да…) В этом новом уравнении в роли нового “b“ выступает дробь b/a, а в роли нового свободного члена — дробь c/a. Можно записывать теорему Виета:
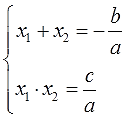
Вот так. Такая модифицированная запись теоремы Виета — более общая. Для любых квадратных уравнений годится — как приведённых (а=1), так и обычных (а≠1). С той лишь разницей, что при а=1 знаменатели исчезают — и теорема обретает свой привычный вид.
Имеет смысл запомнить эту общую форму записи: и для банальной проверки корней пригодится, и, опять же, для более солидных заданий на квадратные уравнения.
Например, надо решить уравнение:
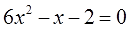
Решаем, получаем корни:
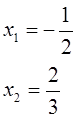
Предположим, вам захотелось проверить, правильно ли вы нашли ваши иксы. Для этого, знамо дело, их надо подставить в исходное уравнение и посчитать результат. Но корни — дробные. Подставлять да считать долго и муторно…
Как проверить корни быстро и с минимумом вычислений? Не проблема! Записываем обобщённую теорему Виета для а=6:
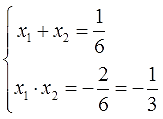
И работаем. Складываем корни:
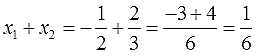
Так, по сумме всё проходит. Осталось перемножить:
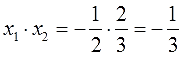
И тут полный порядок! Значит, всё правильно.)
Очередной практический совет:
Найденные корни стараемся проверять! По сумме и произведению. Это здорово уменьшает количество ошибок при решении квадратных уравнений. Если уравнение не является приведённым, то для проверки пользуемся соответствующей модифицированной теоремой Виета.
Итак, мы с вами выяснили, что теорема Виета — штука простая. И очень полезная. И это не только трафаретное решение квадратных уравнений! В ВУЗе, при работе со всякими там пределами, интегралами, дифференциальными уравнениями и прочими прелестями высшей математики, вы ещё не раз вспомните добрым словом знаменитого французского математика с его теоремой.)
Ну что, порешаем?
1. Найдите подбором корни уравнений:
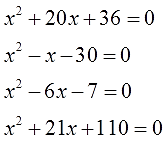
Ответы (в беспорядке):
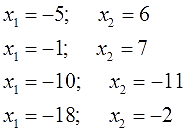
2. Сумма катетов прямоугольного треугольника равна 23 см, а гипотенуза равна 17 см. Найдите больший катет треугольника.
3. Разность корней уравнения 2х2 — 5х + с = 0 равна 1,5. Найдите с.
4. Дано уравнение: x2 — 6x + 4 = 0. Не решая уравнения, найдите сумму кубов его корней.
5. Известно, что х1 и х2 — корни уравнения х2-18х+11 = 0.
Найдите значение выражения:
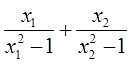
Ответы (в беспорядке):
144; 15; -1; 1
Всё сошлось? Рад за вас! Значит, отныне теорема Виета — не ваша очередная головная боль, а новый надёжный друг и помощник при решении уравнений (и не только квадратных, между прочим!).
Задания 4 и 5 не идут? Корни иррациональные получаются? Это специально.) Да и не нужны они вам… Да, есть там одна загвоздочка. Но алгебра седьмого класса и действия с дробями вам помогут! И этот урок, само собой. И всё получится.)










