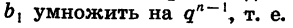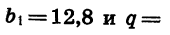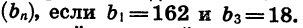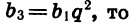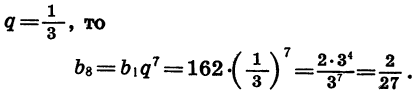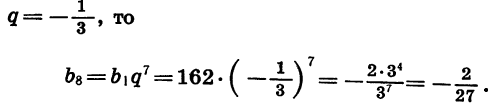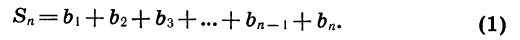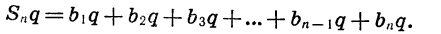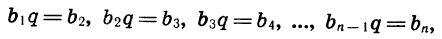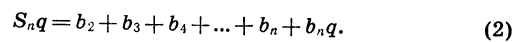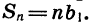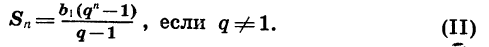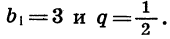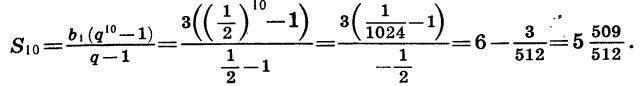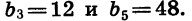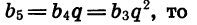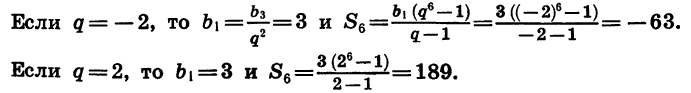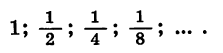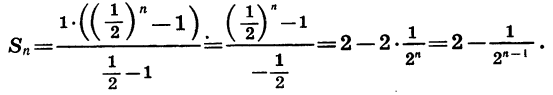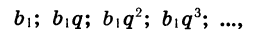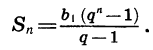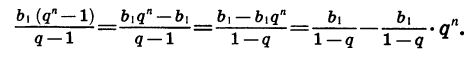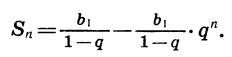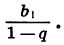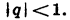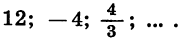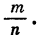Как найти сумму квадратов членов геометрической прогрессии - Сайт, где вы сможете решить свои вопросы

Содержание

Определение геометрической прогрессии
- Формула n-го члена геометрической прогрессии
Сумма первых n членов геометрической прогрессии
- Формула суммы первых n членов геометрической прогрессии
Сумма бесконечно убывающей геометрической прогрессии

Определение геометрической прогрессии

Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.

То есть геометрическая прогрессия определяется рекуррентным соотношением

$[b_{n+1} = b_n cdot q.]$

Теорема 1. Пусть — геометрическая прогрессия со знаменателем Тогда для всех натуральных справедлива формула

$[b_n = b_1cdot q^{n-1}.]$

Доказательство. Воспользуемся рекуррентным определением геометрической прогрессии:

$[b_n = b_{n-1}q = b_{n-2}q^2 = ldots = b_1q^{n-1}.]$

Итак, для n-го члена геометрической прогрессии справедлива формула

$[b_n = b_1cdot q^{n-1}.]$

Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:

$[b_n^2 = b_{n-1}cdot b_{n+1}.]$

Доказательство. Из определения геометрической прогрессии

$[b_n = b_{n-1}cdot q, qquad b_{n+1} = b_n cdot q.]$

Следовательно,

$[frac{b_n}{b_{n-1}} = frac{b_{n+1}}{b_n} = q,]$

откуда

$[b_n^2 = b_{n-1}cdot b_{n+1}.]$

Обратное утверждение тоже верно. Если для всех членов последовательности ${b_n},$ начиная со второго, выполняется равенство $b_n^2 = b_{n-1}cdot b_{n+1},$ то эта последовательность — геометрическая прогрессия.

Пример 1. Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвёртого членов — 30. Найдём первый член и знаменатель прогрессии.

Решение. По условию

$begin{equation*} begin{cases} b_1 + b_3 = 10, \ b_2 + b_4 = 30. end{cases} end{equation*}$

Выразим члены геометрической прогрессии через и : Тогда система запишется в виде

$begin{equation*} begin{cases} b_1 + b_1q^2 = 10, \ b_1q + b_1q^3 = 30. end{cases} end{equation*}$

Разделив второе уравнение системы на первое, получим Следовательно,

Сумма первых n членов геометрической прогрессии

Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :

(1) $begin{equation*}S_n= b_1 + b_2 + ldots + b_n.end{equation*}$

Умножим это равенство на :

или

(2) $begin{equation*}S_n q = b_2 + b_3 + ldots + b_{n+1}.end{equation*}$

Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим $S_n q - S_n = b_{n+1} - b_1.$ Отсюда, так как имеем

$[S_n = frac{b_{n+1} - b_1}{q - 1},]$

или

(3) $begin{equation*}S_n = frac{b_nq - b_1}{q - 1}.end{equation*}$

Так как $b_n = b_1q^{n-1},$ то формулу (3) можно переписать в виде

(4) $begin{equation*}S_n = frac{b_1(q^n - 1)}{q - 1}.end{equation*}$

Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.

Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?

Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии

$[1, 2, 2^2, 2^3, ldots , 2^{63}.]$

По формуле (3) получаем

$[S = frac{2^{63}cdot 2 - 1}{2 - 1} = 2^{64} - 1 = ]$

Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.

Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.

Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.

Сумма бесконечно убывающей геометрической прогрессии

Рассмотрим геометрическую прогрессию ${b_1q^{n-1}}.$ Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.

Сумма бесконечно убывающей геометрической прогресcии выражается формулой

(5) $begin{equation*}S = frac{b_1}{1 - q}.end{equation*}$

Пример 3. Найдём сумму

$[S = frac{1}{2} - frac{1}{4} + frac{1}{8} - frac{1}{16} + ldots.]$

Решение. — сумма бесконечно убывающей геометрической прогрессии с первым членом $b_1 = frac{1}{2}$ и знаменателем $q = -frac{1}{2}.$ По формуле (5) получаем

$[S = frac{frac{1}{2}}{1 + frac{1}{2}} = frac{frac{1}{2}}{frac{3}{2}} = frac{1}{3}.]$

То есть $S = frac{1}{3}.$

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2022 года; проверки требуют 37 правок.

У этого термина существуют и другие значения, см. Прогрессия.

Геометри́ческая прогре́ссия — последовательность чисел $b_{1}$ , $b_{2}$ , $b_{3}$ , ldots (члены прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего члена умножением его на фиксированное число (знаменатель прогрессии). При этом ${displaystyle b_{1}neq 0,qneq 0;b_{n}=b_{n-1}q,nin mathbb {N} ,ngeqslant 2}$ ^[1].

Геометрическая прогрессия называется бесконечно убывающей^[2], если знаменатель прогрессии по абсолютной величине меньше единицы.

Произведением первых членов геометрической прогрессии ${displaystyle left{b_{n}right}}$ называется произведение от $b_{1}$ до b_n , то есть выражение вида ${displaystyle prod limits _{i=1}^{n}b_{i}=b_{1}cdot b_{2}cdot b_{3}cdot ldots cdot b_{n-2}cdot b_{n-1}cdot b_{n}.}$
Обозначение: $P_{n}$ .

Описание[править | править код]

Любой член геометрической прогрессии может быть вычислен по формуле

${displaystyle b_{n}=b_{1}q^{n-1}.}$

Если ${displaystyle b_{1}>0}$ и , прогрессия является возрастающей последовательностью, если , — убывающей последовательностью, а при q<0 — знакочередующейся^[3], при q=1 — стационарной (постоянной).

Своё название прогрессия получила по своему характеристическому свойству:

${displaystyle |b_{n}|={sqrt {b_{n-1}b_{n+1}}},}$

то есть модуль любого члена геометрической прогрессии, кроме первого, равен среднему геометрическому (среднему пропорциональному) двух рядом с ним стоящих членов^[4].

Примеры[править | править код]

Получение новых квадратов путём соединения середин сторон предыдущих квадратов

Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата^[5]^:8—9.
Геометрической является последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — геометрическая прогрессия со знаменателем 2 из тринадцати членов.
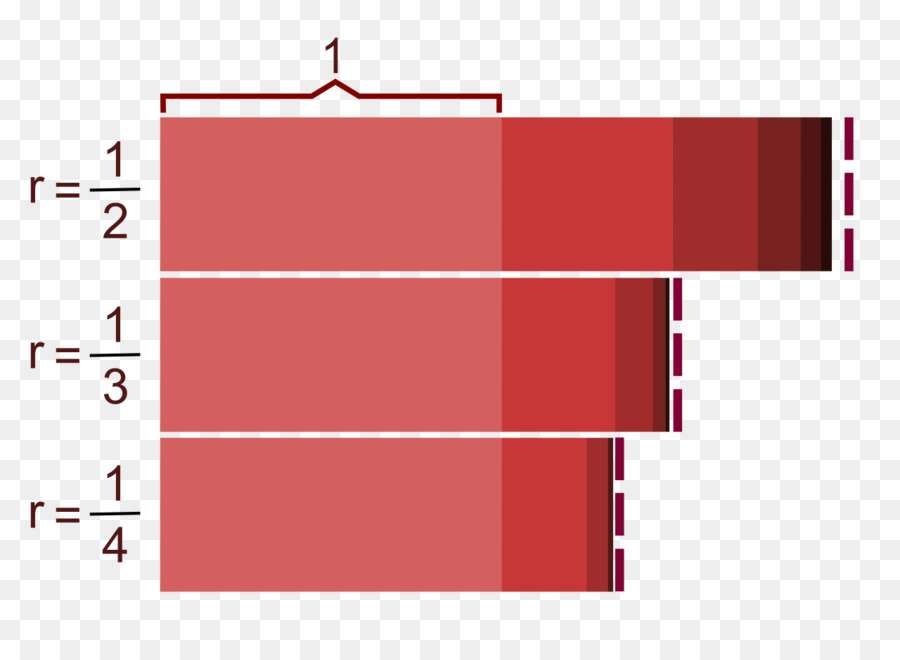
50; 25; 12,5; 6,25; 3,125; … — бесконечно убывающая геометрическая прогрессия со знаменателем 1/2.
4; 6; 9 — геометрическая прогрессия из трёх элементов со знаменателем 3/2.
, , , — стационарная геометрическая прогрессия со знаменателем 1 (и стационарная арифметическая прогрессия с разностью 0).
3; −6; 12; −24; 48; … — знакочередующаяся геометрическая прогрессия со знаменателем −2.
1; −1; 1; −1; 1; … — знакочередующаяся геометрическая прогрессия со знаменателем −1.

Свойства[править | править код]

Свойства знаменателя геометрической прогрессии[править | править код]

Знаменатель геометрической прогрессии можно найти по формулам:

${displaystyle q={dfrac {b_{n+1}}{b_{n}}}}$

Доказательство

По определению геометрической прогрессии.

${displaystyle q={sqrt[{n-k}]{dfrac {b_{n}}{b_{k}}}},{text{где }}k<n;;forall n,forall kin mathbb {N} .}$

Свойства членов геометрической прогрессии[править | править код]

Рекуррентное соотношение для геометрической прогрессии:

${displaystyle b_{n}=b_{n-1}cdot q}$

Доказательство

По определению геометрической прогрессии.

Формула общего (-го) члена:

${displaystyle b_{n}=b_{1}cdot q^{n-1}.}$

Обобщённая формула общего члена:

${displaystyle b_{n}=b_{k}cdot q^{n-k},{text{где }}k<n;;forall n,forall kin mathbb {N} .}$

Доказательство

${displaystyle b_{n}^{2}=b_{n}b_{n}=b_{1}q^{n-1}b_{1}q^{n-1}=b_{1}q^{n-1-i}b_{1}q^{n-1+i}=b_{n-i}b_{n+i}.}$

Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Доказательство

${displaystyle log(b_{n})=log(b_{1}q^{n-1})=log(b_{1})+(n-1)cdot log(q)}$
Формула общего члена арифметической прогрессии:
${displaystyle a_{n}=a_{1}+(n-1)cdot d}$ .
В нашем случае
$a_{1}=log(b_{1})$ ,
.

Доказательство

${displaystyle b_{n}^{2}=b_{n}b_{n}=b_{1}q^{n-1}b_{1}q^{n-1}=b_{1}q^{n-1-i}b_{1}q^{n-1+i}=b_{n-i}b_{n+i}.}$

Пусть ${displaystyle a_{k},a_{l},a_{m}}$ — соответственно -й, -й, -й члены геометрической прогрессии, где . Тогда для всякой такой тройки выполняется комплементарное свойство геометрической прогрессии, называемое тождеством геометрической прогрессии:

${displaystyle b_{k}^{l-m}cdot b_{l}^{m-k}cdot b_{m}^{k-l}=1.}$

Произведение членов геометрической прогрессии начиная с k-го члена, и заканчивая n-м членом, можно рассчитать по формуле

${displaystyle P_{k,n}={dfrac {P_{n}}{P_{k-1}}}.}$

Доказательство

${displaystyle P_{k,n}=prod _{i=k}^{n}b_{i}={frac {prod _{i=1}^{n}b_{i}}{prod _{j=1}^{k-1}b_{j}}}={frac {P_{n}}{P_{k-1}}}.}$

Сумма всех членов убывающей прогрессии:

, то ${displaystyle b_{n}to 0}$

при

, и

${displaystyle S_{n}to {frac {b_{1}}{1-q}}}$

при

Свойства суммы геометрической прогрессии[править | править код]

${displaystyle b_{n+1}=S_{n+1}-S_{n}}$
${displaystyle S_{n}=sigma _{n}cdot b_{1}b_{n}}$

где ${displaystyle sigma _{n}}$ — сумма обратных величин, т. е. ${displaystyle sigma _{n}={dfrac {1}{b_{1}}}+{dfrac {1}{b_{2}}}+cdots +{dfrac {1}{b_{n-1}}}+{dfrac {1}{b_{n}}}}$ .

Свойства произведения геометрической прогрессии[править | править код]

См. также[править | править код]

Арифметическая прогрессия
Арифметико-геометрическая прогрессия
Числа Фибоначчи
Показательная функция
Сумма ряда

Примечания[править | править код]

↑ Геометрическая прогрессия Архивная копия от 12 октября 2011 на Wayback Machine на mathematics.ru
↑ Это название, хотя и является общепринятым, неудачно, так как бесконечно убывающая геометрическая прогрессия является убывающей, только если и первый член, и знаменатель прогрессии положительны.
↑ Геометрическая прогрессия // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Если геометрическая прогрессия является конечной последовательностью, то её последний член таким свойством не обладает.
↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Mathesis, 1923. Архивная копия от 19 мая 2017 на Wayback Machine

Источник

Определение геометрической прогрессии:

Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:

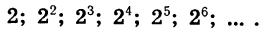
Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.

Определение:

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

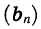
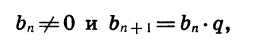
Иначе говоря, последовательность — геометрическая прогрессия, если для любого натурального п выполняются условия

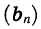
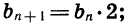
где q — некоторое число. Обозначим, например, через последовательность натуральных степеней числа 2. В этом случае для любого натурального п верно равенство здесь q = 2.

Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т. е. при любом натуральном n верно равенство

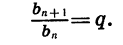
Число q называют знаменателем геометрической прогрессии.

Очевидно, что знаменатель геометрической прогрессии отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.

Приведем примеры.

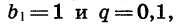
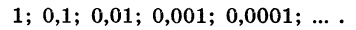
Если то получим геометрическую прогрессию

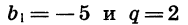
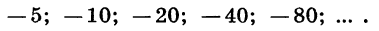
Условиями задается геометрическая прогрессия

Если 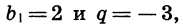то имеем прогрессию

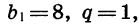
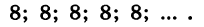
Если то получим геометрическую прогрессию

Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий и вообще любой ее член:

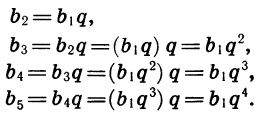
Точно так же находим, что Вообще, чтобы найти мы должны

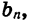
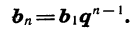
Мы получили формулу n-го члена геометрической прогрессии.

Приведем примеры решения задач с использованием этой формулы.

Пример:

В геометрической прогрессии 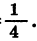Найдем b7.

По формуле n-го члена геометрической прогрессии

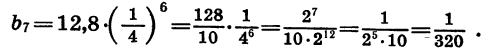
Пример:

Найдем восьмой член геометрической прогрессии

Зная первый и третий члены геометрической прогрессии, можно найти ее знаменатель. Так как

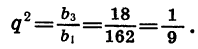
Решив уравнение

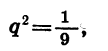
найдем, что

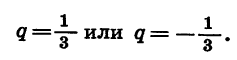
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

Если

Задача имеет два решения:

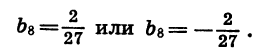
Пример:

После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда, после шести движений поршня, если первоначально давление было 760 мм рт. ст.

Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха, то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде после очередного движения поршня, нужно давление после предыдущего движения поршня умножить на 0,8.

Мы имеем геометрическую прогрессию, первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде (в мм рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно

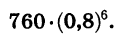
Произведя вычисления, получим:

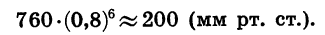
Формула суммы n первых членов геометрической прогрессии

Древняя индийская легенда рассказывает, что изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую — в 2 раза больше, т. е. 2 зерна, на третью — еще в 2 раза больше, т. е. 4 зерна, и т. д. до 64-й клетки. Сколько зерен должен был получить изобретатель шахмат?

Число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:

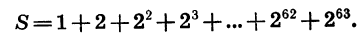
Умножим обе части записанного равенства на знаменатель прогрессии, получим:

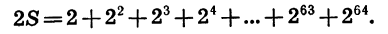
Вычтем почленно из второго равенства первое и проведем упрощения:

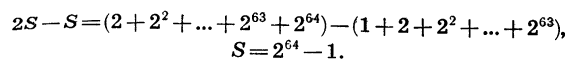
Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.

Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.

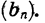
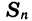
Пусть дана геометрическая прогрессия Обозначим сумму n первых ее членов через :

Умножим обе части этого равенства на q:

Учитывая, что

получим:

Вычтем почленно из равенства (2) равенство (1) и приведем подобные члены:

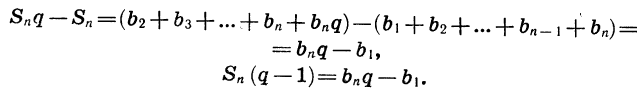
Отсюда следует, что при

Мы получили формулу суммы n первых членов геометрической прогрессии, в которой 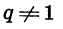. Если q = 1, то все члены прогрессии равны первому члену и

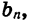
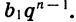
При решении многих задач удобно пользоваться формулой суммы п первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо выражение Получим:

Пример:

Найдем сумму первых десяти членов геометрической прогрессии 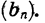в которой

Так как известны первый член и знаменатель прогрессии, то удобно воспользоваться формулой (II). Получим:

Пример:

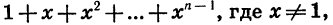
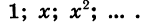
Найдем сумму слагаемые которой являются последовательными членами геометрической прогрессии

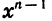
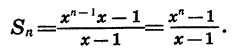
Первый член прогрессии равен 1, а знаменатель равен х. Так как является членом этой прогрессии с номером n, то задача состоит в нахождении суммы п первых ее членов. Воспользуемся формулой (I):

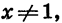
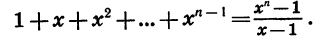
Таким образом, если то

Умножив левую и правую части последнего равенства на х — 1, получим тождество

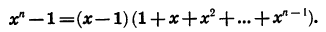
В частности, при n = 2 и n = 3 приходим к известным формулам

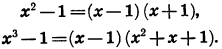
Пример:

Найдем сумму шести первых членов геометрической прогрессии 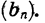если известно, что

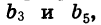
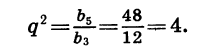
Зная можно найти знаменатель прогрессии q. Так как

Значит,

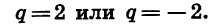
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

Сумма бесконечной геометрической прогрессии при |q|< 1

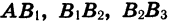
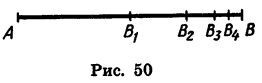
Пусть длина отрезка АВ равна 2 ед. (рис. 50). Отметим точку В1 — середину отрезка А В, затем точку В2 — середину правой его половины, затем точку В3 — середину получившегося справа отрезка и т. д. Длины отрезков и т. д. образуют бесконечную геометрическую прогрессию, знаменатель которой равен

Найдем сумму n первых членов этой прогрессии:

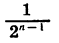
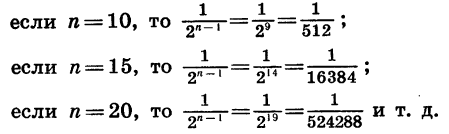
При увеличении числа слагаемых n значение дроби приближается к нулю. Действительно,

Поэтому при неограниченном увеличении n разность 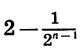становится сколь угодно близкой к числу 2 или, как говорят, стремится к числу 2.

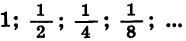
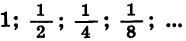
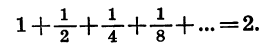
Таким образом, сумма n первых членов геометрической прогрессии при неограниченном увеличении n стремится к числу 2. Число 2 называют суммой бесконечной геометрической прогрессии и пишут:

Это равенство легко истолковать геометрически: сумма длин отрезков 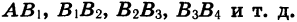равна длине отрезка АВ.

Рассмотрим теперь произвольную геометрическую прогрессию

у которой |q|< 1

Запишем формулу суммы п первых членов прогрессии:

Преобразуем выражение в правой части равенства:

Значит,

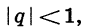
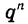
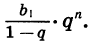
Можно доказать, что если то при неограниченном увеличении n множитель стремится к нулю, а значит, стремится к нулю и произведение Поэтому при неограниченном увеличении n сумма Sn стремится к числу

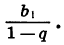
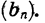
Число называют суммой бесконечной геометрической прогрессии у которой

Это записывают так:

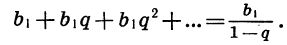
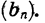
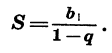
Обозначив сумму прогрессии буквой S, получим формулу

Заметим, что если 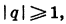то сумма n первых членов геометрической прогрессии при неограниченном увеличении n не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при

Пример:

Найдем сумму бесконечной геометрической прогрессии

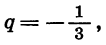
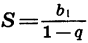
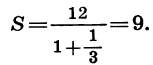
У этой прогрессии значит, условие |q| < 1 выполнено. По формуле получим:

Пример:

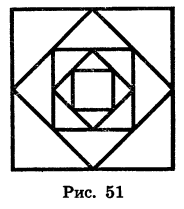
Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. (рис. 51). Найдем сумму площадей всех квадратов.

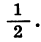
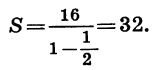
Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен Найдем сумму этой геометрической прогрессии:

Значит, сумма площадей всех квадратов равна 32 см2.

Из курса VIII класса нам известно, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Чтобы выразить рациональное число — целое число, а n — натуральное, в виде бесконечной десятичной дроби, достаточно разделить числитель на знаменатель. Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число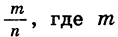. Покажем на примере, как с помощью формулы суммы бесконечной геометрической прогрессии можно представить бесконечную десятичную периодическую дробь в виде отношения

Пример:

Представим бесконечную десятичную периодическую дробь 0,(18) в виде обыкновенной дроби.

По аналогии с конечными десятичными дробями представим бесконечную десятичную дробь 0,(18) в виде суммы:

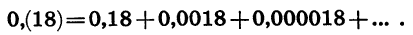
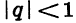
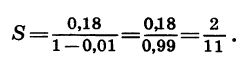
Слагаемые в правой части равенства — члены геометрической прогрессии, у которой первый член равен 0,18, а знаменатель равен 0,01, т. е. условие выполнено. Найдем сумму этой прогрессии:

Значит,

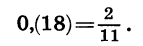
Таким же способом можно представить в виде обыкновенной дроби любую бесконечную десятичную периодическую дробь.

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

Геометрическая прогрессия представляет собой один из самых интересных числовых рядов, которые рассматривают в школьном курсе алгебры. Данная статья посвящена частному случаю упомянутого ряда: убывающей бесконечной геометрической прогрессии и сумме ее членов.

О каком ряде чисел пойдет речь?

Прогрессией геометрической называют одномерную последовательность действительных чисел, которые связаны друг с другом следующим соотношением:

a2 = a1*r, a3 = a2*r, a4 = a3*r, …., an = an-1*r

Обобщая выражения выше, можно записать следующее равенство:

Вам будет интересно:Альбом – это всегда творчество

an = a1*rn-1

Как понятно из приведенных записей, an – это элемент прогрессии с номером n. Параметр r, на который следует умножить n-1 элемент, чтобы получить n-й, называют знаменателем.

Какими свойствами обладает описанная последовательность? Ответ на вопрос зависит от величины и знака r. Возможны следующие варианты:

Знаменатель r положительный и больше 1. Прогрессия в этом случае всегда будет возрастать по модулю, при этом абсолютное значение ее членов может и убывать, если a1 будет отрицательным.
Знаменатель r отрицательный и больше 1. В таком случае члены прогрессии будут появляться с чередованием знака (+ и -). Подобные ряды мало интересны для практики.
Модуль знаменателя r меньше 1. Этот ряд называется убывающим, причем независимо от знака r. Именно эта прогрессия представляет большой практический интерес, о ней пойдет речь в данной статье.

Вам будет интересно:Римская нумерация: история и значение

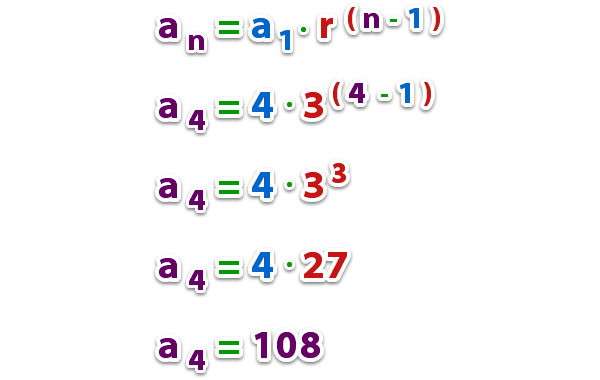
Формула для суммы

Получим для начала выражение, которое позволит вычислить сумму произвольного количества элементов заданной прогрессии. Начнем решать эту задачу в лоб. Имеем:

Sn = a1+a2+a3+..+an

Приведенным равенством можно пользоваться, если необходимо посчитать результат для небольшого числа членов (3-4 слагаемых), каждый из которых определяется по формуле для n-го члена (см. предыдущий пункт). Однако если слагаемых становится много, то в лоб считать неудобно и можно допустить ошибку, поэтому пользуются специальной формулой.

Обе части равенства выше умножим на r, получаем:

r*Sn = r*a1+r*a2+r*a3+..+r*an = a2+a3+a4+…+an+1

Теперь попарно вычтем левые и правые части этих двух выражений, имеем:

r*Sn – Sn = a2+a3+a4+…+an+1 – (a1+a2+a3+..+an) = an+1 – a1

Выражая сумму Sn и пользуясь формулой для члена an+1, получим:

Sn = (an+1 – a1)/(r-1) = a1*(rn – 1)/(r-1)

Таким образом, мы получили общую формулу для суммы первых n слагаемых рассматриваемого типа числового ряда. Заметим, что формула справедлива, если r≠1. В последнем случае имеет место простой ряд одинаковых чисел, сумма которых вычисляется как произведение одного числа на их количество.

Как находить сумму бесконечной геометрической прогрессии убывающей?

Чтобы ответить на этот вопрос, следует напомнить, что ряд будет убывающим, когда |r|<1. Воспользуемся полученной в предыдущем пункте формулой для Sn:

Sn = a1*(rn – 1)/(r-1)

Заметим, что любое число, модуль которого меньше 1, при возведении в большие степени стремится к нулю, то есть r∞->0. Проверить этот факт можно на любом примере:

r = -1/2, тогда (-1/2)**10 ≈ 9,7*10-4, (-1/2)**20 ≈ 9,5*10-7 и так далее.

Установив этот факт, обратим внимание на выражение для суммы: при n->∞ оно будет переписано следующим образом:

S∞ = a1*(r∞ – 1)/(r-1) = a1/(1-r)

Получился интересный результат: сумма бесконечной прогрессии геометрической убывающей стремится к конечному числу, которое не зависит от количества слагаемых. Она определяется лишь первым членом и знаменателем. Заметим, что знак суммы однозначно определяется знаком a1, поскольку знаменатель всегда является положительным числом (1-r>0).

Сумма квадратов бесконечной геометрической прогрессии убывающей

Название пункта определяет задачу, которую следует решить. Для этого воспользуемся методикой, которая полностью аналогична той, что применялась для вывода общей формулы для Sn. Имеем первое выражение:

Mn = a12 + a22 + a32 + … + an2

Умножим обе части равенства на r2, записываем второе выражение:

r2*Mn = r2*a12 + r2*a22 + r2*a32 + … + r2*an2 = a22 + a32 + a42 … + an+12

Теперь находим разность этих двух равенств:

r2*Mn – Mn = a22 + a32 + a42 … + an+12 – (a12 + a22 + a32 + … + an2) = an+12 – a12

Выражаем Mn и используем формулу для n-го элемента, получаем равенство:

Mn = (an+12 – a12)/(r2-1)=a12*(r2n-1)/(r2-1)

В предыдущем пункте было показано, что r∞ -> 0, тогда конечная формула примет вид:

M∞ = a12*/(1-r2)

Сравнение двух полученных сумм

Сравним две формулы: для бесконечной суммы и бесконечной суммы квадратов на примере следующей задачи: сумма бесконечной геометрической прогрессии равна 2, известно, что речь идет об убывающей последовательности, для которой знаменатель равен 1/3. Необходимо найти бесконечную сумму квадратов этого ряда чисел.

Воспользуемся формулой для суммы. Выразим a1:

S∞ = a1/(1-r) => a1 = S∞*(1-r)

Подставляем это выражение в формулу для суммы квадратов, имеем:

M∞ = a12*/(1-r2) = S∞2*(1-r)2/(1-r2) = S∞2*(1-r)/(1+r)

Мы получили искомую формулу, теперь можно подставлять известные из условия данные:

M∞ = S∞2*(1-r)/(1+r) = 22*(1-1/3)/(1+1/3) = 2

Таким образом, мы получили для бесконечной суммы квадратов такое же значение, что и для простой суммы. Заметим, что этот результат справедлив только для этой задачи. В общем случае M∞ ≠ S∞.

Задача на вычисление площади прямоугольника

Каждому школьнику известна формула S = a * b, которая определяет площадь прямоугольника через его стороны. Мало кто знает, что задачу нахождения площади этой фигуры можно легко решить, если воспользоваться суммой бесконечной геометрической прогрессии. Покажем, как это делается.

Разделим мысленно прямоугольник пополам. Площадь одной половинки примем за единицу. Теперь поделим вторую половинку еще пополам. Получим две половинки, одну из которых поделим еще пополам. Эту процедуру будем продолжать до бесконечности (см. рисунок ниже).

В итоге площадь прямоугольника в выбранных нами единицах будет равна:

S∞ = 1+1/2+1/4+1/8+…

Видно, что эти слагаемые являются элементами убывающего ряда, у которого a1 = 1 и r = 1/2. Воспользовавшись формулой для бесконечной суммы, получим:

S∞ = 1 /(1-1/2) = 2

В выбранном нами масштабе половинка прямоугольника (одна единица) соответствует площади a*b/2. Это означает, что площадь всего прямоугольника равна:

S∞ = 2*a*b/2 = a*b

Полученный результат является очевидным, тем не менее он показал, как можно применять убывающую прогрессию для решения задач в геометрии.

Источник

Определение

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.

Другими словами, последовательность (b_n) – геометрическая последовательность, если для натурального n выполняются условия:

b_n+1= b_n×q,

где q некоторое число, которое называется знаменатель прогрессии, и b_n≠0

Примером такой последовательности может быть ряд чисел 2; 10; 50; 250;…., откуда видно, что каждое последующее больше предыдущего в пять раз, значит, каждый член равен предыдущему, умноженному на одно и то же число 5. Или, например, ряд чисел 20; -2; 0,2; -0,02……, где видно, что каждое последующее умножали на одно и то же число (-0,1).

Так как по определению геометрической прогрессии мы имеем одно и то же число, то это и есть число q. Оно называется «знаменатель» геометрической прогрессии. Он находится путем деления соседних членов – последующего на предыдущий, то есть q=bn+1bn. Знаменатель не может быть равным нулю!

Для того чтобы задать геометрическую прогрессию, надо знать ее первый член и знаменатель. Например, если b₁=4, q=3, то получим прогрессию: 4; 12; 36; ….и так далее. Ну, а зная первый член и знаменатель, можно найти любой член геометрической прогрессии: b₂=b₁q; b₃=(b₁q)q=b₁q²; b₄==((b₁q)q)q=b₁q³. Так можно продолжать и дальше, но из этих записей видно, что можно найти n-ый член геометрической последовательности, если умножить первый член на знаменатель, степень которого на 1 меньше порядкового номера искомого члена, то есть bn=b1 qn−1 . Мы получили формулу n-ого члена геометрической прогрессии.

Формула n-ого члена геометрической прогрессии

bn=b1 ×qn−1

Рассмотри на примерах применение формулы bn=b1 qn−1 для указанного члена геометрической прогрессии.

Пример №1. Найти четвертый член геометрической прогрессии, если известно, что b₁=6, q=3. Составляем формулу для b₄:

b4=b1 q4−1=b1 q3

Подставляем в формулу значения, указанные в задании и вычисляем результат: b4=6×33=162.

Найти шестой член геометрической прогрессии 2; -6;……. Здесь для нахождения b₆ надо знать знаменатель q. Для его нахождения надо -6 разделить на 2, получим -3, то есть q=-3. Теперь составляем формулу для b₆, подставляем значения и вычисляем ответ:

b6=b1 q6−1=b1 q5=2×(−3)5=−486

Свойство геометрической прогрессии

Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего ее членов. Формула:

b2n=bn−1×bn+1

Верным является и утверждение, обратное данному: если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность чисел является геометрической прогрессией.

Другими словами, с помощью данной формулы можно найти неизвестный член геометрической прогрессии, соседние члены которого известны. Рассмотрим применение данного свойства на примерах.

Пример №2. Найти b₅, если задана геометрическая прогрессия, в которой b₄=32, b₆=128. Составляем формулу, подставляем в нее значения и вычисляем:

b25=b5−1×b5+1=b4 ×b6 =32×128=4096

Этим действием мы нашли квадрат пятого члена геометрической прогрессии, поэтому извлекаем квадратный корень из числа 4096 для нахождения значения b₅: b₅=√4096=64

Найти у, если дана геометрическая прогрессия …..24; у; 96. Видим, что у находится между соседними известными числами 24 и 96. Поэтому, следуя свойству, умножаем данные числа и извлекаем квадратный корень из полученного числа: у=√24×96=√2304=48.

Формула суммы n первых членов геометрической прогрессии

Формула суммы членов геометрической прогрессии с известными членами

Sn=bnq−b1q−1 , где q≠1

Для нахождения суммы по данной формуле нужно знать первый и последний член геометрической прогрессии, а также ее знаменатель.

Также есть вторая формула, по которой можно находить сумму нескольких первых членов прогрессии, зная только первый ее член и знаменатель:

Формула суммы членов геометрической прогрессии с известным первым членом и знаменателем

Sn=b1(qn−1)q−1, где q≠1

Рассмотрим применение данных формул на примере, решив его двумя способами.

Пример №3. Найти сумму пяти первых членов геометрической прогрессии, если известно, что b₁=2; b₅=162; q=-3.

Способ №1 (первая формула). Составим формулу для нахождения S₅:

S5=b5q−b1q−1

Подставим значения b₁=2; b₅=162 и найдем результат:

S5=162(−3)−2−3−1=−486−2−4=−488−4=122

Способ №2 (вторая формула).

Sn=b1(qn−1)q−1

Для решения нам нужен первый член и знаменатель: b₁=2; q=-3. Составим формулу:

S5=b1(q5−1)q−1

Подставим в формулу данные значения и вычислим сумму:

S5=2((−3)5−1)−3−1=2(−243−1)−4=−488−4=122

Таким образом, мы увидели, что у нас получился один и тот же результат 122 в обоих способах решения. Выбор формулы зависит от данных в условии задачи.

Задание OM1420222

У Кати есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 400 см, а после каждого следующего отскока от асфальта подлетал на высоту в 2 раза меньше предыдущей. После какого по счету отскока высота, на которую подлетит попрыгунчик, станет меньше 20 см?

Определим, к какой последовательности относится наша задача. По условию имеем, что после каждого следующего отскока от асфальта подлетал на высоту в 2 раза меньше предыдущей. Это геометрическая прогрессия. Теперь выпишем, что известно по условию и определим, что надо найти: первый член прогрессии b₁=400, знаменатель q=12, n – количество отскоков, значит, найти надо n при b_n<20.

Подставим в формулу n-ого члена геометрической прогрессии наши данные:

b_n=b₁q^n-1=400∙(12)n−1<20

Разделим обе части неравенства на 400: (12)n−1<120

Будем рассматривать случаи, начиная с n=3: (12)3−1<120; (12)2<120; (14)<120 неверно

При n=4: (12)4−1<120; (12)3<120; (18)<120 неверно

При n=5: (12)5−1<120; (12)4<120; (116)<120 неверно

При n=6: (12)6−1<120; (12)5<120; (132)<120 верно. Следовательно, после 6 отскока высота, на которую подлетит попрыгунчик, станет меньше 20 см.

К данной задаче можно сделать проверку, а также она является простейшим способом для её решения. Рассмотрим этот способ:

1 отскок – 400 см

2 отскок – 200 см (разделили на 2, так как по условию сказано, что с каждым отскоком высота уменьшалась в 2 раза)

3 отскок – 100 см

4 отскок – 50 см

5 отскок – 25 см

6 отскок – 12,5 см, а это меньше, чем 20 см, как требуется в условии. Поэтому пишем в ответ число 6.

Ответ: 6

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 6.3k

Источник

Определение геометрической прогрессии

Сумма первых n членов геометрической прогрессии

Сумма бесконечно убывающей геометрической прогрессии

Описание[править | править код]

Примеры[править | править код]

Свойства[править | править код]

Свойства знаменателя геометрической прогрессии[править | править код]

Свойства членов геометрической прогрессии[править | править код]

Свойства суммы геометрической прогрессии[править | править код]

Свойства произведения геометрической прогрессии[править | править код]

См. также[править | править код]

Примечания[править | править код]

Формула суммы n первых членов геометрической прогрессии

Сумма бесконечной геометрической прогрессии при |q|< 1

О каком ряде чисел пойдет речь?

Формула для суммы

Как находить сумму бесконечной геометрической прогрессии убывающей?

Сумма квадратов бесконечной геометрической прогрессии убывающей

Сравнение двух полученных сумм

Задача на вычисление площади прямоугольника

Формула суммы n первых членов геометрической прогрессии

Вам также может понравиться

Как найти цветок папоротника ночью

Как найти эмоджи каменного лица

Как составить психологический портрет убийцы

Добавить комментарий Отменить ответ