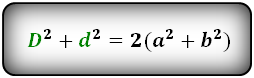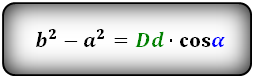Как найти сумму квадратов диагоналей параллелограмма - Сайт, где вы сможете решить свои вопросы

Сумма квадратов диагоналей параллелограмма

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

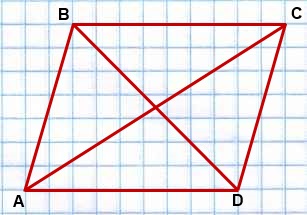
Пусть AC и BD – диагонали параллелограмма ABCD.
Докажем, что .
Противоположные стороны параллелограмма равны , поэтому равенство, которое нужно доказать, можно записать в виде:
.

Самый простой способ – воспользоваться теоремой косинусов.
Из треугольника ABC:

Из треугольника BDC:

Сложим полученные равенства:

AB=CD, BC=AD (по свойству параллелограмма), тогда

$angle ABC + angle BCD = 180 ^{circ}$ (как односторонние углы при параллельных сторонах AB и CD), поэтому .

, что и требовалось доказать.

Теорема косинусов помогает найти решение многих задач по планиметрии из вариантов ЕГЭ по математике.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Сумма квадратов диагоналей параллелограмма» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Теорема. (Свойства диагоналей параллелограмма).

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

$[A{C^2} + B{D^2} = A{B^2} + B{C^2} + C{D^2} + A{D^2}]$

Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:

$[A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})]$

Дано:

ABCD — параллелограмм,

AC и BD — диагонали.

Доказать:

$[A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})]$

Доказательство:

I споссоб.

1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.

2) Рассмотрим прямоугольный треугольник BDK.

По теореме Пифагора

$[B{D^2} = B{K^2} + K{D^2}.]$

3) Аналогично, из прямоугольного треугольника ACF

$[{A{C^2} = C{F^2} + A{F^2}}]$

4) Сложим почленно полученные равенства:

$[begin{array}{l} B{D^2} = B{K^2} + K{D^2}\ underline {A{C^2} = C{F^2} + A{F^2}} \ A{C^2} + B{D^2} = B{K^2} + C{F^2} + K{D^2} + A{F^2} end{array}]$

BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому

$[A{C^2} + B{D^2} = 2B{K^2} + K{D^2} + A{F^2}]$

5) Из прямоугольного треугольника ABK по теореме Пифагора

$[B{K^2} = A{B^2} - A{K^2}.]$

6) KD=AD-AK, AF=AD+FD, поэтому

$[A{C^2} + B{D^2} = ]$

$[ = 2(A{B^2} - A{K^2}) + {(AD - AK)^2} + {(AD + FD)^2}]$

7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).

Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,

$[A{C^2} + B{D^2} = ]$

$[ = 2(A{B^2} - A{K^2}) + {(AD - AK)^2} + {(AD + AK)^2}]$

Раскрываем скобки:

$[A{C^2} + B{D^2} = 2A{B^2}underline { - 2A{K^2}} + ]$

$[ + A{D^2}underline{underline { - 2 cdot AD cdot AK}} + underline {A{K^2}} + ]$

$[ + A{D^2}underline{underline { + 2 cdot AD cdot AK}} + underline {A{K^2}} ]$

Упрощаем

$[A{C^2} + B{D^2} = 2A{B^2} + 2A{D^2}]$

$[A{C^2} + B{D^2} = 2{(A{B^2} + AD^2}).]$

Что и требовалось доказать.

II способ.

Свойство диагоналей параллелограмма можно рассматривать как следствие из теоремы косинусов.

Этот способ доказательства будет рассмотрен в следующий раз.

Источник

Формулы суммы квадратов диагоналей и разности квадратов сторон параллелограмма:

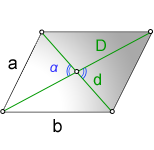
a, b – стороны параллелограмма

D – большая диагональ

d – меньшая диагональ

α – острый угол между диагоналями

Формула суммы квадратов диагоналей:

Формула разности квадратов сторон:

Формулы площади параллелограмма

Формула периметра параллелограмма

Все формулы по геометрии

Источник

Теорема

Сумма квадратов диагоналей параллелограмма равна сумме квадратов
всех его сторон.

Доказательство

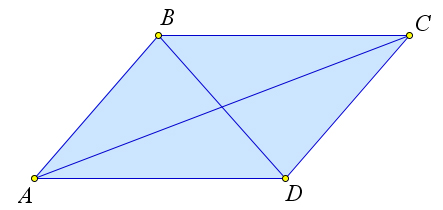
Рассмотрим параллелограмм $ABCD$.

Докажем, что $AC^2+BD^2=AB^2+BC^2+CD^2+AD^2$.

По теореме косинусов для треугольника $ABC$ имеем: $AC^2=AB^2+BC^2-2cdot ABcdot BCcos{B}$.

По теореме косинусов для треугольника $BAD$ имеем:
$BD^2=AB^2+AD^2-2cdot ABcdot ADcos{A}$.

Но так как $ABCD$ – это параллелограмм, то $angle A=180^circ-angle B, BC=AD$.

Следовательно, $cos{A}=-cos{B}$ и $BD^2=AB^2+BC^2+2cdot ABcdot BCcos{B}$.

Складывая это равенство с выражением для $AC^2$ получим:
$AC^2+BD^2=AB^2+BC^2+CD^2+AD^2$.

Источник

Параллелограмм и его свойства

Параллелограмм определение

Параллелограмм

Противоположные углы параллелограмма равны.
Высота перпендикулярно основанию параллелограмма.
Cумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: (d_1^2+d_2^2=2(a^2+b^2));
Диагонали параллелограмма пересекаются в точке: (AO = OC, BO = OD)
Сумма углов четырехугольника прилегающих к любой стороне равна (180°).
Сумма квадратов диагоналей равна сумме квадратов сторон в параллелограмме: (d^2_1+d_2^2=2a^2+2b^2.)
Биссектрисы противоположных углов параллелограмма всегда параллельны.
Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°).
Сторону параллелограмма можно найти по диагонали и углу между ними:

(a= sqrt{d_1^2 + d^2_2 – 2d_1d_2cosa } )

Также сторону параллелограмма можно найти по диагоналям и другой стороне:

(a = { sqrt{2d_1^2+ 2d_1^2 – 4b_2^2 } over 2} )

(b = { sqrt{2d_1^2+ 2d_1^2 – 4a_2^2 } over 2} )

Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

Сумма квадратов диагоналей параллелограмма

Теорема

Доказательство

Вам также может понравиться

Как найти стороны в многоугольнике зная угол

Как найти английский переводчик онлайн

Как составить текст про футбол

Добавить комментарий Отменить ответ