Как найти сумму квадратов медиан прямоугольного треугольника

Примечание. В данном уроке изложены теоретические материалы и решение задач по геометрии на тему “медиана в прямоугольном треугольнике”. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. Почти наверняка курс будет дополнен.

Свойства медианы прямоугольного треугольника

Определение медианы

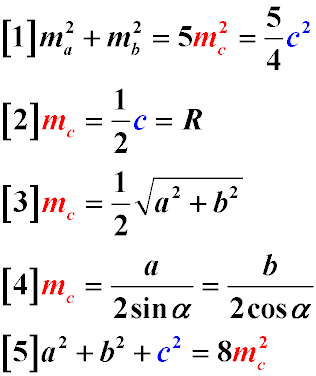
Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.

• Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
• Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
• Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
• Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов (Формула 3)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
• Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)

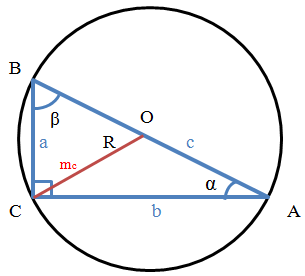
Обозначения в формулах:

a, b – катеты прямоугольного треугольника

c – гипотенуза прямоугольного треугольника

Если обозначить треугольник, как ABC, то 

ВС = а

AC = b

AB = c

(то есть стороны a,b,c – являются противолежащими соответствующим углам)

m_a – медиана, проведенная к катету а 

m_b – медиана, проведенная к катету b

m_c – медиана прямоугольного треугольника, проведенная к гипотенузе с

α (альфа) – угол CAB, противолежащий стороне а

Задача про медиану в прямоугольном треугольнике

Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно,  3 см и 4 см. Найдите гипотенузу треугольника

Решение

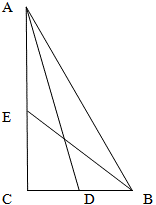
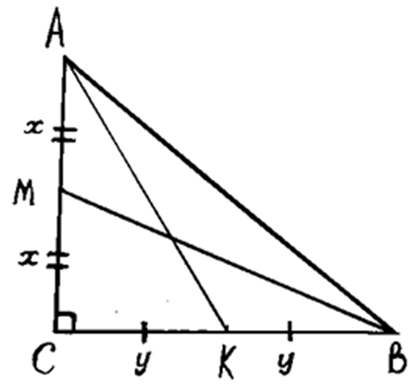
Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике. В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y). 

Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC – общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора   

AC² + CD² = AD²

Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4x² + y² = 9 

Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
По теореме Пифагора:
EC² + BC²  = BE²

Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x² + 4y²  = 16

Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений. 
4x² + y² = 9
x² + 4y²  = 16 

Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5x² + 5y² = 25  
5( x² + y² ) = 25
x² + y² = 5 

AB² = 4 х 5
AB² = 20
AB = √20 = 2√5  

Ответ: длина гипотенузы равна 2√5     

0
 

 Угол между высотой и медианой треугольника |

Описание курса

| Медіана прямокутного трикутника 

Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

• BC = 2AD
• AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.

Медиана в прямоугольном треугольнике

Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.

Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:

Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.

Например:

12 Comments

Информация очень хорошая. Правда не помогла мне решить задачу, которую мой сын не решил на контрольной. приведу условие:
Из прямого угла треугольника проведена медиана на гипотенузу. Длина медианы 6см. Определить катеты.

Петр, данных для определения катетов недостаточно. Длина гипотенузы в 2 раза больше длины медианы — 12 см. Это всё, что можно сказать по данным условия.

не правда надо провести высоту из прямого угла дальше все получится. один катет равен 6 а второй 2 корня из 22

Сумма квадратов катетов равна квадрату гипотенузы. Проверим 6^2+(2*корень из 22)^2
=36+4*22=36+88=124. Квадрат гипотенузы 12^2=144

попробуйте составить уравнение,обозначив 1 из катетов через х а 2-ой катет обозначьте буквами…x^2+BC^2=12^2…да числа не очень,но это 1 способ..решаю дальше:BC^2=12^2-x^2
BC^2=11x
X^2+11X=144
X^2=12
x(1 катет)=корню из 12,а «-ой катет=11 корней из 12….решал на основе теоремы пифагора

задача имеет бесконечное кол-во решений. решение возможно только в виде формулы или графика, где описана зависимость между катетами и гипотенузой

Да просто треугольник медианой делится на два треугольника с одинаковыми катетами, а дальше как уже предлагалось выше Пифагор во спасение))

А кто вам сказал, что медиана в прямоугольном треугольнике является еще и высотой? Откуда у вас два треугольника с одинаковыми катетами?

Спасибо за понятное объяснение, но у нас задача немного другая.
В прямоугольном треугольнике АВС угол С= 90 градусов,медиана ВВ1 равна 10 см.Найдите медианы АА1 СС1, если известно, что АС=12 см.( используя т.Пифагора.

1) Рассмотрим треугольник BB1C. В нём угол С равен 90 градусов, BB1=10 см, B1C=6 см (так как BB1 — медиана). По теореме Пифагора находим BC: BC=8 см. 2) Рассмотрим треугольник AA1C. В нём угол С равен 90 градусов, AC=12 см, AA1=4 см (так как BB1 — медиана). По теореме Пифагора находим AA1: AA1=4√10 см.3) Из треугольника ABC по теореме Пифагора найдём AB: AB=4√13 см. 4) CC1=1/2 AB (как медиана, проведённая к гипотенузе), CC1=2√13 см.
Где-то так.

Свойства медианы прямоугольного треугольника

Определение медианы

• Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины угла. Точка их пересечения называется центром тяжести треугольника (относительно редко в задачах для обозначения этой точки используется термин “центроид”),
• Медиана разбивает треугольник на два равновеликих треугольника.
• Треугольник делится тремя медианами на шесть равновеликих треугольников.
• Большей стороне треугольника соответствует меньшая медиана.

Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.

• Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
• Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
• Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
• Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов (Формула 3)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
• Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)

Задача про медиану в прямоугольном треугольнике

Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно, 3 см и 4 см. Найдите гипотенузу треугольника

Решение

Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике. В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y).

Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC – общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора

AC 2 + CD 2 = AD 2

Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4x 2 + y 2 = 9

Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
По теореме Пифагора:
EC 2 + BC 2 = BE 2

Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x 2 + 4y 2 = 16

Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений.
4x 2 + y 2 = 9
x 2 + 4y 2 = 16

Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5x 2 + 5y 2 = 25
5( x 2 + y 2 ) = 25
x 2 + y 2 = 5

Обратимся к исходному треугольнику ABC. По теореме Пифагора
AC 2 + BC 2 = AB 2

Так как длина каждого из катетов нам “известна”, мы приняли, что их длина равна 2x и 2y, то есть
4x 2 + 4y 2 = AB 2
Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки
4 ( x 2 + y 2 ) = AB 2
Чему равно x 2 + y 2 мы уже знаем (см. выше x 2 + y 2 = 5), поэтому просто подставим значения вместо x 2 + y 2

AB 2 = 4 х 5
AB 2 = 20
AB = √20 = 2√5

Ответ: длина гипотенузы равна 2√5

[spoiler title=”источники:”]

http://profmeter.com.ua/communication/learning/course/course7/lesson364/

[/spoiler]

Светило науки – 165 ответов – 2648 раз оказано помощи

По свойствам прямоугольного треугольника, медиана, проведенная к гипотенузе равняется половине гипотенузы, следовательно:

Две других медианы вычислим по теореме Пифагора:
[tex]m^2_b=a^2+frac{1}{4}b^2
m^2_a=frac{1}{4}a^2+b^2[/tex]
Таким образом, сумма квадратов медиан будет равна:

Так как катет, лежащий против угла  30°, равен половине гипотенузы, то

Так как катет, лежащий против угла  30°, равен половине гипотенузы, то

– медианы в прямоугольном треугольнике пересекаются в
одной точке, а точка пересечения делит их в соотношении два к одному считая от
вершины, из которой проведена медиана;

– медиана, проведённая из
вершины прямого угла к гипотенузе, равна половине гипотенузу;

– медиана, опущенная на гипотенузу прямоугольного треугольника, равна
радиусу окружности, описанной вокруг данного прямоугольного треугольника;

– сумма
квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам
медианы, опущенной на гипотенузу;

– сумма
квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти
четвёртых квадрата гипотенузы;

– медиана,
опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов
катетов;

– медиана,
опущенная на гипотенузу, равна частному от деления длины катета на два синуса
противолежащего катету острого угла;

– медиана,
опущенная на гипотенузу, равна частному от деления длины катета на два косинуса
прилежащего катету острого угла;

– сумма квадратов сторон
прямоугольного треугольникаравна восьми квадратам медианы, опущенной на его
гипотенузу;

– медиана, проведённая к катету  а, равна
половине корня квадратного из суммы учетверённого квадрата катета  b  и квадрата катета  а;

– медиана, проведённая к катету  b, равна
половине корня квадратного из суммы учетверённого квадрата катета  а  и квадрата катета  b;

Обозначения в формулах.

a, b – катеты
прямоугольного треугольника;

с – гипотенуза
прямоугольного треугольника.

Если обозначить треугольник, как  АВС, то

ВС = а, АС = b, АВ = с

(то есть стороны  а,
b, с – являются
противолежащими соответствующим углам).

т_а –
медиана, проведённая к катету  а;

т_b – медиана,
проведённая к катету  b;

т_с –
медиана, проведённая к гипотенузе  с;

α (альфа) –
угол  САВ,
противолежащий стороне  а.

ЗАДАЧА:

Две стороны треугольника равны  6 см  и  8 см. Медианы, проведённые к этим сторонам, пересекаются
под прямым углом. Найдите третью сторону треугольника.

РЕШЕНИЕ:

Начертим
чертёж.

Обозначим  

АN = х см. ВМ
= у см.

Тогда 

АО = ²/₃ х,
NО = ¹/₃ у,

ВО = ²/₃ х,
МО = ¹/₃ у.

АМ² = ОМ²
+ ОА²,

ВN² = ОВ² + ОN²,

5х² + 5у² = 225,

х² + у²
= 45.

АВ² = ВО²
+ ОА² =

= ⁴/₉ (х²
+ у²) = 20, то

АВ = √͞͞͞͞͞20 = 2√͞͞͞͞͞5 см.

ЗАДАЧА:

В треугольнике  АВС:

АВ = √͞͞͞͞͞41, ВС = 13, 

ВН – высота, опущенная на
сторону  АС, ВН = 5. 

Найдите
длину медианы АМ.

РЕШЕНИЕ:

Начертим чертёж.

В прямоугольном
треугольнике  ВНС  по
теореме Пифагора 

В прямоугольном
треугольнике  АВН  по
теореме Пифагора 

Опустим из точки  М  перпендикуляр  МD  на сторону АС, МD – средняя линия треугольника  ВНС, следовательно

МD = ¹/₂ ВН = ⁵/₂,

НD = DС = ¹/₂ НС = 6.

Тогда в прямоугольном треугольнике  АМD

∠ АDМ = 90°,

АD = АН + НD =

= 4 + 6 = 10,

МD = ⁵/₂.

По теореме Пифагора

ЗАДАЧА:

В прямоугольном треугольнике медианы, проведённые к
катетам равны  √͞͞͞͞͞52  и √͞͞͞͞͞73. Найдите длину
гипотенузы.

РЕШЕНИЕ:

Начертим чертёж.

Проведём медианы  АК
 и  ВМ. Пусть 

АК = √͞͞͞͞͞52,

ВМ = √͞͞͞͞͞73,

х – половина длины
стороны  АС,

у – половина длины
стороны  ВС. Тогда из
прямоугольных треугольников  АСК  и  ВСМ  имеем:

АК² = АС²
+ СК²,

ВМ² = МС²
+ ВС²

тогда  составим систему уравнений:

отсюда

5(х² + у²) = 125,

х² + у²
= 25,

АК² = 4(х²
+ у²).

АВ = 10.

ЗАДАЧА:

Медианы  СМ  и 
ВN  прямоугольного
треугольника  АВС (∠ С = 90°), перпендикулярны. Найдите катеты, если гипотенуза
равна  с.

РЕШЕНИЕ:

Начертим чертёж.

МА = МС = МВ = ^с/₂.

Пусть  NО = х,

Тогда 

ВО = ²/₃ х, МО = ^с/₆.

МВ² = МО² + ВО²,

Биссектриса прямоугольного треугольника.

Биссектрисою прямоугольного треугольника называют отрезок
биссектрисы угла треугольника, который соединяет его вершину с точкой на противоположной
стороне треугольника.

Биссектриса прямоугольного треугольника делит противоположную сторону на
отрезки, соответственно пропорциональные двум другим сторонам.

Связь угла  (α)  между
высотой и биссектрисой, проведёнными из прямого угла, определяется через острые
углы этого треугольника.

ЗАДАЧА:

Биссектриса прямого угла
прямоугольного треугольника образует с гипотенузой углы, один из которых
равен  70°. Найдите острые углы этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

∠ DBC = ∠ DBA = 45°,

∠ DCB = 180° – 70° – 45° = 65°,

∠ ADB = 180° – 70° = 110°,

∠ CAB = 180° – 110° – 45° = 25°.

ЗАДАЧА:

Биссектриса прямого угла
прямоугольного треугольника делит гипотенузу на отрезки длиной  15
см  и 
20
см. Найдите длины отрезков гипотенузы, на которые её делит высота треугольника.

РЕШЕНИЕ:

Биссектриса треугольника делит сторону на
отрезки, пропорциональные прилежащим сторонам.

Следовательно,

СВ
: АС = 15 : 20.

Пусть коэффициент этого
отношения будет  х. Тогда

АС = 20х, ВС
= 15х,

АВ = 20 + 15 = 35.

По теореме Пифагора:

АС² + ВС² = АВ^2,

400х²
+ 225х² = 1225.

х = √͞͞͞͞͞1,96 = 1,4,

АС = 20 ∙ 1,4 = 28,

ВС = 15 ∙ 1,4 = 21.

Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между
катетом и высотой.

ВС² = АВ ∙ ВН,

441 = 35 ∙ ВН,

ВН
=
12,6,

АН = 35 – 12,6 =
22,4.

ЗАДАЧА:

Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен  14°.
Найдите меньший угол этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

Так как связь угла  (α)  между высотой и биссектрисой, проведёнными из
прямого угла, определяется через острые углы этого треугольника следующим
образом:

∠ ВАС
= 45° – α,

∠ ВСА
= 45° + α,

∠ α = ∠ МВD = 14°,

то меньший угол
треугольника  ВАС  будет равен:

∠ ВАС = 45° – 14° = 31°.

Задания к уроку 9