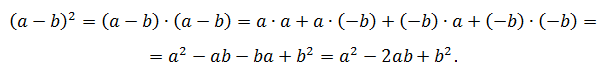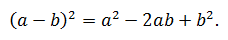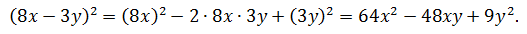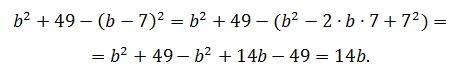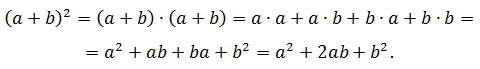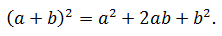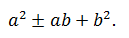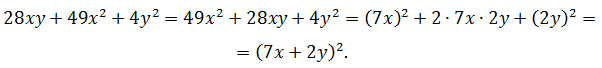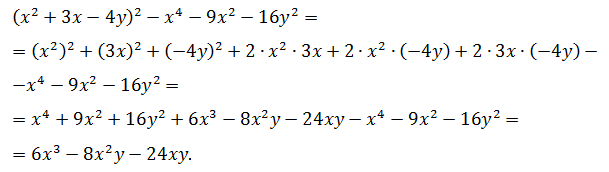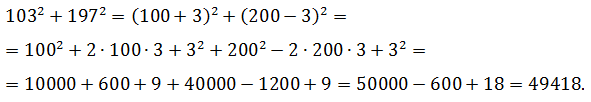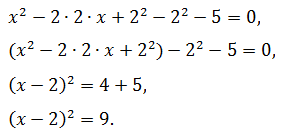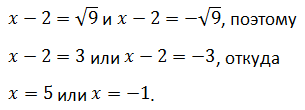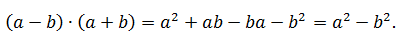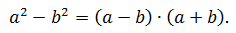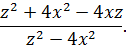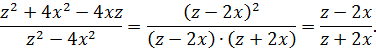Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b)2 = a2 ± 2ab + b2
Существует множество формул для решения подобных выражений, и дело не ограничивается квадратами. При помощи формул легко подсчитать куб разности или сумму многочленов n-ной степени. Мы легко можем подсчитать даже выражение (a + b + c)3, однако формулы сокращенного умножения для простого выражения как:
a2 + b2
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
a2 + b2 = (a + ib) × (a – ib),
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a2 + b2 = (a + b)2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
- 5 и 0 = 25;
- 1 и 4 = 25;
- 8 и 1 = 64;
- 4 и 7 = 64.
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
f2 = a2 + b2 + c2 + d2,
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Sum of squares refers to the sum of the squares of the given numbers, i.e., it is the addition of squared numbers. The squared terms could be two terms, three terms, or “n” number of terms, the first “n” odd or even terms, a series of natural numbers or consecutive numbers, etc. In statistics, the value of the sum of squares tells the degree of dispersion in a dataset. For this, we need to first find the mean of the given data, then the variation of each data point from the mean, square them, and finally, add them. In algebra, we use the (a + b)2 identity to determine the sum of the squares of two numbers. The formula that determines the sum of the squares of the first “n” natural numbers is derived with the help of the sum of the squares of the first “n” natural numbers. We perform these fundamental arithmetic operations, which are necessary for both algebra and statistics. There are various methods to determine the sum of squares of given numbers.
Sum of Squares Formula
The sum of the square formula is appliable for two, three, and up to n terms which are explained below:
Sum of squares for two numbers
Let a and b be two real numbers, then the formula for the addition of squares of the two numbers is given as follows:
a2 + b2 = (a + b)2 − 2ab
Proof:
From the algebraic identities, we have,
(a + b)2 = a2 + 2ab + b2
Now, subtract 2ab on both sides.
(a + b)2 − 2ab = a2 + 2ab + b2 − 2ab
a2 + b2 = (a + b)2 − 2ab
Hence, proved.
Sum of squares for three numbers
Let a, b, and c be three real numbers, then the formula for the addition of squares of the three numbers is given as follows:
a2 + b2 + c2 = (a +b + c)2 − 2ab − 2bc − 2ca
Proof:
From the algebraic identities, we have,
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
By subtracting 2ab, 2bc, and 2ca on both sides, we get,
a2 + b2 + c2 = (a + b + c)2 − 2ab − 2bc − 2ca
Hence, proved
Sum of squares for “n” Natural Numbers
Natural numbers are also known as positive integers and include all the counting numbers, starting from 1 to infinity. If 1, 2, 3, 4,… n are n consecutive natural numbers, then the sum of squares of “n” consecutive natural numbers is represented by 12 + 22 + 32 +… + n2 and symbolically represented as Σn2.
The formula for the sum of squares of the first “n” natural numbers is given as follows:
∑n2 = [n(n+1)(2n+1)]/6
Sum of Squares of First “n” Even Numbers
The formula for the sum of squares of the first “n” even numbers, i.e., 22 + 42 + 62 +… + (2n)2 is given as follows:
∑(2n)2 = 22 + 42 + 62 +… + (2n)2
∑(2n)2 = [2n(n+1)(2n+1)]/3
Sum of Squares of First “n” Odd Numbers
The formula for the sum of squares of the first “n” odd numbers, i.e., 12 + 32 + 52 +… + (2n – 1)2, can be derived using the formulas for the sum of the squares of the first “2n” natural numbers and the sum of squares of the first “n” even numbers.
∑(2n-1)2 = 12 + 32 + 52 + … + (2n – 1)2
∑(2n-1)2 = [n(2n+1)(2n-1)]/3
Proof:
∑(2n –1)2 = [12 + 22 + 32 + … + (2n – 1)2 + (2n)2] – [22 + 42 + 62 + … + (2n)2]
Now, apply the formula for the addition of squares of “2n” natural numbers and “n” even natural numbers, and we get;
∑(2n–1)2 = 2n/6 (2n + 1)(4n + 1) – (2n/3) (n+1)(2n+1)
∑(2n–1)2 = n/3 [(2n+1)(4n+1)] – 2n/3 [(n+1)(2n+1)]
Now, take out the common terms.
∑(2n–1)2 = n/3 (2n+1) [4n + 1 – 2n – 2]
∑(2n–1)2 = [n(2n+1)(2n–1)]/3
Hence, proved.
Sum of Squares in Statistics
Sum of squares of n data points = ∑ni=0 (xi – x̄)2
∑ = represents sum
xi = each value in the set
x̄ = mean of the values
xi – x̄ = deviation from the mean value
(xi – x̄)2 = square of the deviation
n = number of terms in the series
In statistics, the value of the sum of squares tells the degree of dispersion in a dataset. It evaluates the variance of the data points from the mean and aids in a better understanding of the data. The large value of the sum of squares indicates that there is a high variation of the data points from the mean value, while the small value indicates that there is a low variation of the data from its mean. Follow the steps given below to find the total sum of squares in statistics.
- Step 1: Count the number of data points in the given dataset.
- Step 2: Now, calculate the mean of the given data.
- Step 3: Subtract each data point from the mean calculated in step 2.
- Step 4: Now, determine the square of the difference obtained in step 3.
- Step 5: Finally, add the squares that we have determined in step 4.
Solved Examples based on Sum of Squares
Example 1: Find the sum of the given series: 12 + 22 + 32 +…+ 552.
Solution:
To find the value of 12 + 22 + 32 +…+ 552.
From the sum of squares formula for n terms, we have
∑n2 = 12 + 22 + 32 +…+ n2 = [n(n+1)(2n+1)] / 6
Given, n = 55
= [55(55+1)(2×55+1)] / 6
= (55 × 56 × 111) / 6
= 56,980
Thus, the sum of the given series is 56,980.
Example 2: Find the value of (32 + 82), using the sum of squares formula.
Solution:
To find the value of 32 + 82
Given: a = 3 and b = 8.
From the sum of squares formula, we have
a2 + b2 = (a + b)2 − 2ab
⇒ 32 + 82 = (3 + 8)2 − 2(3)(8)
= 121 – 2(24)
= 121 − 48
= 73.
Hence, the value of (32 + 82) is 73.
Example 3: Find the sum of squares of the first 25 even natural numbers.
Solution:
To find the value of 22 + 42 + 62 +… + 482+ 502.
= 22( 12 + 22 + 32 +…+252)
From the sum of squares formula for n terms, we have
∑n2 = [n(n+1)(2n+1)]/6
Here, n = 25
22( 12 + 22 + 32 +…+252) = 4[25(25+1)(2(25)+1)/6]
= (2/3) × (25) × (26) × (51)
= 22,100
Hence, the sum of squares of the first 25 even natural numbers is 22,100.
Example 4: A dataset has points 2, 4, 13, 10, 12, and 7. Find the sum of squares for the given data.
Solution:
Given: We have 6 data points 2, 4, 13, 10, 12, and 7.
The sum of the given data points = 2 + 4 + 13 + 10 + 12 + 7 = 48.
The mean of the given data is given by,
Mean, x̄ = Sum / Number of data points
= 48 / 6
= 8
So, the sum of squares is given by,
∑ni=0 (xi – x̄)2 = (2 – 8)2 + (4 – 8)2 + (13 – 8)2 + (10 – 8)2 + (12 – 8)2 + (7 – 8)2
= (–6)2 + (–4)2 + (5)2 + (2)2 + (4)2 + (–1)2
= 36 + 16 + 25 + 4 + 14 + 1
= 96
Hence, the sum of squares for the given data is 96.
Example 5: Calculate the sum of the squares of 4, 9, and 11 using the sum of squares formula for three numbers.
Solution:
To find the value of 4, 9, and 11.
Given, a = 4, b = 9, and c = 11.
From the sum of squares formula, we have
a2 + b2 + c2 = (a + b +c)2 − 2ab − 2bc − 2ca
42 + 92 + 112 = (4 + 9 + 11)2 −(2×4×9) − (2×9×11) − (2×11×4)
= 576 − 72 − 198 − 88
= 218
Hence, the value of (42 + 92 + 112) is 218.
Example 6: Find the sum of squares of the first 10 odd numbers.
Solution:
The sum of squares of the first 10 odd numbers: 12 + 32 + 52 +… +172 + 192
We know that,
The sum of squares of first “n” Odd Numbers ∑(2n–1)2 = [n(2n+1)(2n–1)]/3
Here, n is 10.
= [10×(2×10 + 1)(2×10 – 1)]/3
= [10 × 21 × 19]/3
= 10 × 7 × 19 = 1,330
Hence, the value of the sum of squares of the first 10 odd numbers is 1330.
FAQs based on Sum of Squares
Question 1: What is the Sum of Squares Error?
Answer:
Sum of squares error, also known as the residual sum of squares, is the difference between the actual value and the predicted value of the data.
Question 2: What Is the Expansion of Sum of Squares Formula?
Answer:
a2 + b2 formula is known as the sum of squares formula in algebra and it is read as a square plus b square. Its expansion is expressed as a2 + b2 = (a + b)2 – 2ab.
Question 3: Write the Sum of Squares Formula used in Algebra.
Answer:
The sum of squares formula used in algebra are:
- a2 + b2 = (a + b)2 − 2ab
- a2 + b2 + c2 = (a +b + c)2 − 2ab − 2bc − 2ca
Question 4: Write the sum of squares of the first five even numbers.
Answer:
The sum of squares of the first five even numbers is given by:
∑(2n)2 = [2n(n+1)(2n+1)]/3
putting n = 5
∑(2×5)2 = [2×5×(5+1)×(2×5+1)]/3
= 220
Онлайн калькулятор для расчета суммы квадратов целых чисел.
Как пользоваться
Введите целые числа, разделяя между собой запятой. Вводить можно положительные и отрицательные числа. После нажмите на красную кнопку «Рассчитать». Программа автоматически вычислит сумму квадратов заданных чисел.
Определение
Квадратом числа называется результат умножения числа на себя или возведение во вторую степень. Обозначается как надстрочный знак — 2.
Формула нахождения суммы квадратов целых чисел
S = a2 + b2 + c2 + d2.
Где:
a, b, c, d — целые числа,
S — сумма квадратов.
Задание
Введите в верхнее поле числа: 2,12,22,32,42. Равна ли сумма их квадратов 3240 или 3420?
Этот вопрос вряд ли имеет какое-то важное практическое значение, однако очень интересен как элемент занимательной математики, в особенности, если для нахождения универсальной формулы использовать графический метод.
Давайте рассмотрим следующее:
Видите здесь какую-нибудь закономерность?
Сходу найти универсальную формулу для n-й суммы квадратов не так-то просто. Есть, кстати алгебраический путь, но он мне сейчас совершенно не интересен. Я бы хотел пойти другим путем – графическим.
Что нам для этого нужно?
Давайте представим сумму квадратов:
В виде пирамидки из 14 кубиков, которая будет выглядеть так:
Пирамидка состоит из 3-х уровней. В сумме кубиков – 14, как и описывает выражение выше.
Теперь, задача состоит в том, чтобы складывая эти пирамидки получить фигуру типа куба или параллелепипеда, т.е объекта который можно легко описать.
Если долго мучиться, то получится такой параллелепипед:
Его ширина та же, что и основание пирамидки, обозначим за “n”. Соответственно его длина 2n+1, а высота n+1.
Чтобы построить такую фигуру нам понадобилось 6 пирамидок.
Далее, составляем неравенство:
В левой его части мы находим объем фигуры (количество кубиков) исходя из того, что знаем какой конфигурации была исходная пирамидка, сколько в ней было кубиков и сколько таких пирамидок нужно, чтобы выстроить параллелепипед.
А в правой части, мы просто нашли объем фигуры умножив длину на высоту, на ширину.
Исходя из этого равенства, можно вывести, что сумма квадратов до любого числа n равна:
Ну вот и все. Делов-то. Надеюсь, было интересно и понятно. Оставляйте комментарии, делитесь публикацией в соцсетях, да и вообще, не забывайте ставить лайк и обязательно подпишитесь, если этого до сих пор не сделали.
Сумма квадратов
Сумма квадратов встречается в ходе преобразования числовых и буквенных выражений. Как с ней работать?
Поскольку сумма квадратов является составной частью формул полного квадрата суммы и разности, можно попробовать применить одну из этих формул.
Формула полного квадрата суммы состоит из трёх слагаемых — сумма квадратов двух слагаемых плюс удвоенное произведение этих слагаемых. Следовательно, для получения полного квадрата к сумме квадратов двух выражений следует прибавить удвоенное произведение этих выражений, и, чтобы выражение не изменилось, вычесть это произведение:
Аналогично, для получения полного квадрата разности следует из суммы квадратов двух выражений вычесть удвоенное произведение этих выражений и тут же прибавить его:
Рассмотрим, как эти рассуждения могут быть применены на практике.
Теперь используем данные условия:
Эти рассуждения применяются, например, в приложении теоремы Виета, когда не решая квадратного уравнения, требуется найти сумму квадратов его корней и т.п.
Источник
Квадрат суммы и разности
Квадрат суммы
Выражение (a + b) 2 — это квадрат суммы чисел a и b. По определению степени выражение (a + b) 2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что
Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:
Многочлен a 2 + 2ab + b 2 называется разложением квадрата суммы.
Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.
Пример. Возвести в квадрат выражение 3x 2 + 2xy.
Решение: Чтобы не производить дополнительных преобразований, воспользуемся формулой квадрата суммы. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:
Квадрат разности
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:
Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.
Пример. Представьте квадрат разности в виде трёхчлена:
Решение: Используя формулу квадрата разности, находим:
Теперь преобразуем выражение в многочлен стандартного вида:
Разность квадратов
Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
Из правила следует, что общая формула разности квадратов выглядит так:
Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.
Пример. Преобразуйте произведение в двучлен:
В примере мы применили формулу разности квадратов справа налево, то есть, нам дана была правая часть формулы, а мы преобразовали её в левую:
На практике все три рассмотренные формулы применяются и слева направо, и справа налево, в зависимости от ситуации.
Источник
Решение формулы суммы квадратов двух чисел
АННОТАЦИЯ
В настоящей статье нами впервые предложено решение формулы сокращенного произведения, которая может широко применена в решении различных математических задач, равенств и неравенств, а также для упрощения сложных алгебраических выражений, имеющих широкое практическое применение в науке и технике.
ABSTRACT
In this article, we first proposed a solution to the abbreviated product formula, which can be used in solving various mathematical problems, equalities and inequalities, as well as to simplify complex algebraic expressions that have wide practical applications in science and technology.
Ключевые слова: формулы сокращенного произведения, сумма квадратов двух чисел.
Keywords: formulas of short multiplication, sum of squares two numbers.
Известно, что при решении задач во всех разделах математики очень часто используют формулы сокращенного произведения (ФСУ) [1. 163-182, 2. 115, 3. 134]. Эти формулы удачно используются при упрощении сложных математических выражений, при решении алгебраических, тригонометрических уравнений, неравенств, геометрических задач, учебных и научных проблем различной сложности. Ниже приведены официально всем известные ФСУ в табличном виде, из учебников Алгебры для 7 класса:
Таблица 1.
Формулы сокращенного умножения
Формула
Название
(a+b) 2 =a 2 +2ab+b 2
Квадрат суммы двух чисел
Квадрат разности двух чисел
Square of difference
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
Куб суммы двух чисел
Куб разности двух чисел
Cube of difference
Сумма кубов двух чисел
Разность кубов двух чисел
Difference of cubes
Разность квадратов двух чисел
Difference of squares
Сумма квадратов двух чисел (Примечание: не разлагающаяся на члены) [8]
Sum of squares (Note: not expands) [8,10]
Наглядно видно из таблицы 1, что приведенные в ней формулы 1, 2; 3, 4; 5, 6; 7, 8 являются формулами-парами, которые отличаются нежели только со знаками у отдельных членов в левой части равенства. Однако, решение для урувнения формулой a 2 +b 2 (8) до настоящего времени ни в официальных источниках, также в учебной и научной литературе не была приведена 1. Тому можно убедиться после ознакомления в электронных интернет учебниках на английском, так и на других языках. В них формула (8) указана как “not expands” – «не разлагающаяся на члены» 8. Также, во всех учебниках для средних образовательных школ по математике, так и в пособиях для ВУЗов Узбекистана, России и Европейских стран, написанные на узбекском, английком, так и на русском языках, формула (8), до настоящего времени обозначается как, “не разлагающаяся на члены”.
В настоящей статье нами впервые предложена конкретное решение для формулы (8), для разложения суммы квадратов двух чисел на многочлены. Она имеет решение следующего вида:
/Mamarakhmonov.files/image001.png)
Доказательство. Результат последовательного произведения многочленов в правой части формулы (8), должны равняться сумме квадратов двух чисел, в левой части равенства. Для этого применяем правила последовательного умножения для многочленов к выражениям в скобках, в правой части равенства:
Примечание. Члены с одинаковыми абсолютными значениями, но с различными знаками взаимно сокращаются, как показано ниже:
/Mamarakhmonov.files/image003.png)
/Mamarakhmonov.files/image004.png)
Конец доказательства.
Предложенная нами формула для суммы квадратов двух чисел (8) является инновационной, новой и имеет в дальнейшем практическое применение как в математике, информатике, ИТ, в точных науках в целом, так и в других отраслях науки и техники.
Список литературы
Источник
Сумма квадратов всех целых чисел
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b) 2 = a 2 ± 2ab + b 2
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a 2 + b 2 = (a + b) 2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Источник
Для успешного решения математических задач часто бывает необходимо уметь преобразовывать созданные выражения. Для этого применяют базовые знания, формулы сокращённого умножения, в том числе, квадрат суммы и квадрат разности.
Они помогают упрощать громоздкие записи, более рационально подходить к приведению дробей к одному знаменателю, решению уравнений и задач по геометрии, тригонометрии, математическому анализу, физике, химии, экономическим дисциплинам и многим другим наукам.
Поэтому среди многих разделов математики школьная алгебра занимает базовую приоритетную позицию, дающую основы вычислений для смежных предметов.
Формула квадрата разности
Для получения формулы применяют правило умножения многочлена на многочлен: нахождение суммы произведений каждого слагаемого одной скобки на каждое слагаемое второй скобки, учитывая, что квадрат отрицательного числа равен квадрату положительного:
Если запомнить правило, то необходимость постоянно прописывать эту цепочку равенств исчезает.
Квадрат разности двух выражений равен сумме квадратов каждого из выражений без их удвоенного произведения:
Примеры задач с решением
Задача №1
При использовании формулы получается:
Задача №2
Формула квадрата суммы и неполного квадрата суммы
Также легко, как и в предыдущем случае, выводится эта формула:
Квадрат суммы двух выражений равен сумме квадратов каждого из них плюс их удвоенное произведение:
Многие школьники, начинающие знакомиться с этим материалом, часто теряют двойку во втором слагаемом правой части, получая
Однако, в этом случае, возникает неполный квадрат суммы (или разности), который на множестве действительных чисел не раскладывается на множители.
Обе формулы применяются не только для раскрытия скобок, но и для разложения на множители, что в свою очередь упрощает приведение к одному знаменателю, сокращение дробей, решение уравнений высоких степеней.
Примеры задач с решением
Задача №3
Преобразовать трёхчлен в квадрат двучлена:
Поскольку квадраты находятся на втором и третьем местах, поменяем слагаемые между собой и подготовим выражение для применения формулы:
Возведение во вторую степень суммы трёх и более слагаемых выполняется аналогично: необходимо возвести в квадрат каждый элемент, записать все возможные удвоенные произведения и сложить полученные результаты.
Правила возведения в степени более высоких порядков возникают, когда выполняется умножение одинаковых многочленов несколько раз.
Возможность выполнять возведение в квадрат больших чисел, не используя калькулятор, является одним из преимуществ сокращённого умножения.
Задача №4
Выполнить раскрытие скобок и упростить:
Задача №5
Для каждого слагаемого применяется одно из правил возведения в квадрат, затем производится суммирование результатов:
Решая квадратные уравнения, вместо поиска дискриминанта выделяют полный (точный) квадрат среди слагаемых, расположенных в левой части. В правую сторону собираются оставшиеся элементы.
Задача №6
Первые два слагаемых левой части полностью удовлетворяют формуле квадрата суммы. Соотнеся их с соответствующими элементами правила, определяют, прибавляют и вычитают третье, затем сворачивают в точный квадрат, остальные члены алгебраической суммы переносят в правую сторону:
Решениями исходного уравнения являются корни уравнений
Разность квадратов
Ещё одной формулой сокращённого умножения является разность квадратов. Она получается при умножении суммы двух выражений на их разность.
Читается справа налево.
Разность квадратов двух выражений равна произведению разности этих выражений на их сумму:
Применение последней записи справа налево есть раскрытие скобок более удобным способом, чем простое умножение многочленов.
Разложение на множители позволяет судить о наличии целых или натуральных корней квадратного уравнения.
Пример задачи с решением
Задача №7
В числителе записан квадрат разности, а в знаменателе – разность квадратов двух выражений. Применяя соответствующие формулы, получается искомый результат:
В большинстве случаев разницы, как сворачивать квадрат двучлена, не существует. Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить
Онлайн калькуляторы помогают выполнять преобразования. Однако, поскольку формулы сокращённого умножения являются базовым материалом школьного курса, то лучше не просто получить результат, но и понять, каким образом к нему пришли.
Источник
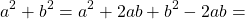
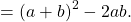
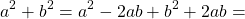
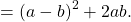
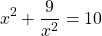



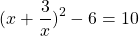
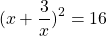
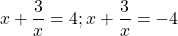
/Mamarakhmonov.files/image002.png)
/Mamarakhmonov.files/image005.png)