Пусть ABCD — данный параллелограмм. Введём прямоугольную систему координат так, как показано на рисунке 283. Если AD = BC = a, а точка В имеет координаты (b; с), то точка D имеет координаты (а; 0), а точка С — координаты (а + b; с). Используя формулу расстояния между двумя точками, находим: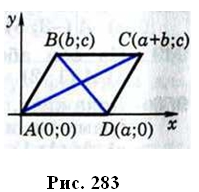
АВ2 = b2 + с2, AD2 = а2, АС2 = (а + b)2 + с2, BD2 = (а – b)2 + с2. Отсюда получаем:
АВ2 + ВС2 + CD2 + DA2 = 2 (АВ2 + AD2) = 2 (а2 + b2 + с2),
АС2 + BD2 = (а + b)2 + с2 + (а – b)2 + с2 = 2 (а2 + b2 + с2).
Таким образом,
АВ2 + ВС2 + CD2 + DA2 = АС2 +BD2, что и требовалось доказать.
Теорема. (Свойства диагоналей параллелограмма).
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
![]()
Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:
![]()
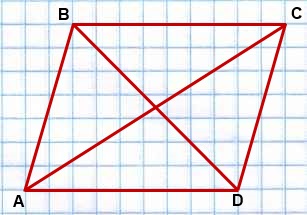
Дано:
ABCD — параллелограмм,
AC и BD — диагонали.
Доказать:
![]()
Доказательство:
I споссоб.

1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.
2) Рассмотрим прямоугольный треугольник BDK.
По теореме Пифагора
![]()
3) Аналогично, из прямоугольного треугольника ACF
![]()
4) Сложим почленно полученные равенства:
![Rendered by QuickLaTeX.com [begin{array}{l} B{D^2} = B{K^2} + K{D^2}\ underline {A{C^2} = C{F^2} + A{F^2}} \ A{C^2} + B{D^2} = B{K^2} + C{F^2} + K{D^2} + A{F^2} end{array}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-9097ac166774298003b917d601c588e8_l3.png)
BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому
![]()
5) Из прямоугольного треугольника ABK по теореме Пифагора
![]()
6) KD=AD-AK, AF=AD+FD, поэтому
![]()
![]()
7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).
Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,
![]()
![]()
Раскрываем скобки:
![]()
![]()
![]()
Упрощаем
![]()
![]()
Что и требовалось доказать.
II способ.
Свойство диагоналей параллелограмма можно рассматривать как следствие из теоремы косинусов.
Этот способ доказательства будет рассмотрен в следующий раз.
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
- В параллелограмме противоположные стороны и противоположные углы равны.
- Диагонали параллелограмма точкой пересечения делятся пополам.
- Диагональ параллелограмма делит параллелограмм на два равных треугольника.
- Точка пересечения диагоналей — центр симметрии параллелограмма.
- Биссектриса любого угла параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы параллелограмма, проведенные из противоположных углов, параллельны.
- Биссектрисы параллелограмма, проведенные из соседних углов, перпендикулярны.
- Угол между высотами, проведенными из тупого угла параллелограмма, равен острому углу параллелограмма.
- Угол между высотами, проведенными из острого угла параллелограмма, равен тупому углу параллелограмма.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон параллелограмма.
- Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Частные случаи параллелограмма: прямоугольник, квадрат, ромб. Следовательно, все эти фигуры обладают свойствами, присущими параллелограмму.
Прямоугольник — параллелограмм, у которого все углы равны.
Отличительное свойство прямоугольника: диагонали прямоугольника равны.
Ромб — параллелограмм, у которого все стороны равны.
Отличительное свойство ромба: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат — параллелограмм, у которого все стороны и углы равны.
Отличительное свойство квадрата: диагонали квадрата равны, взаимно перпендикулярны и делят углы квадрата пополам.
Площадь параллелограмма:
- Площадь параллелограмма через сторону и высоту, проведенной к этой стороне: S=a·ha=b·hb.
- Площадь параллелограмма через стороны и угол между ними: S=a·b·sinφ.
- Площадь параллелограмма через диагонали и угол между ними: S=0,5·d1·d2·sinφ.
- Площадь параллелограмма через радиус вписанной окружности и сторону(верна только для параллелограмма, в который можно вписать окружность): S=2·a·r.
- Площадь параллелограмма через радиус вписанной окружности и угол между сторонами(верна только для параллелограмма, в который можно вписать окружность): S=4r2/sinφ.
Формулы суммы квадратов диагоналей и разности квадратов сторон параллелограмма:
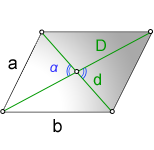
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
Формула суммы квадратов диагоналей:
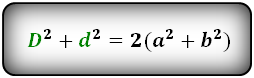
Формула разности квадратов сторон:
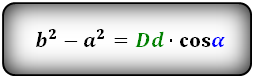
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
