Как найти сумму матриц в excel

В этой статье рассмотрены операции сложения и вычитания над матрицами одного порядка, а также операции умножения матрицы на число. Примеры решены в MS EXCEL.

Операция сложения определена только для матриц одного порядка. Т.е. нельзя говорить о сложении матриц разной размерности. Также неопределена операция сложения матрицы и числа. Напротив, операция умножения матрицы на число определена.

Сумма двух матриц

А

и

В

– это матрица, элементы которой равны сумме соответствующих элементов матриц

А

и

В.

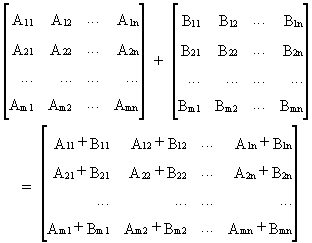
В MS EXCEL операцию сложения матриц реализовать элементарно.

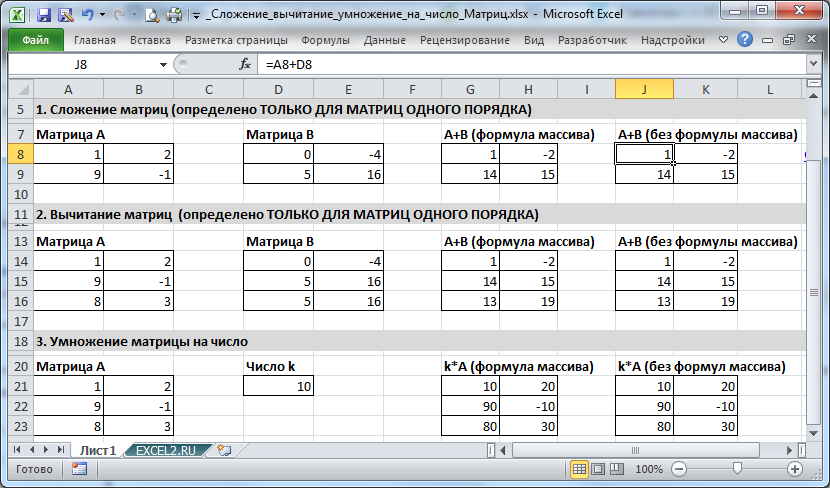
Поместив матрицу А размерности 2х2 в диапазон

А8:В9

, а матрицу B той же размерности 2х2 в диапазон

D8:E9,

в ячейке

J8

введем формулу

=A8+D8

. Скопировав формулу в нужные ячейки, например, с помощью

Маркера заполнения

, получим матрицу А+В.

Аналогичного результата можно добиться с использованием

формулы массива

. Выделив диапазон

G

8:H9

в

Строке формул

введите формулу

=A8:B9+D8:E9

и нажмите

CTRL+SHIFT+ENTER

. Преимущество формулы массива состоит в том, что невозможно удалить отдельные элементы матрицы А+В (появится окно

Невозможно удалить часть массива

).

Понятно, что операция вычитания матриц в MS EXCEL реализуется аналогично (см.

файл примера

).

Умножение матриц на число

Операция умножения матрицы на число определена для матриц любого порядка.

Произведение матрицы А и числа k – это

матрица, элементы которой получаются умножением всех элементов исходной матрицы А на число k.

В MS EXCEL это реализовано с помощью формулы

=A21*$D$21

(предполагается, что матрица находится в диапазоне

А21:В23

, а число в ячейке

D21

). Обратите внимание, что в формуле использована

абсолютная адресация

на ячейку с числом. Это позволяет при копировании формулы (для отображения всех элементов матрицы k*А) ссылаться на одну и ту же ячейку с числом.

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).

Порядок применения формулы массива:

1. Выделить диапазон, где должен появиться результат действия формулы.
2. Ввести формулу (как и положено, со знака «=»).
3. Нажать сочетание кнопок Ctrl + Shift + Ввод.

В строке формул отобразится формула массива в фигурных скобках.

Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.



Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

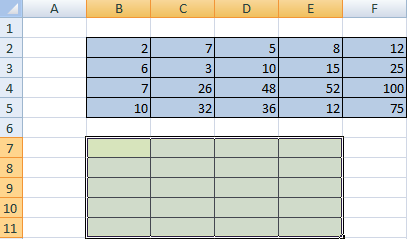
• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.



• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

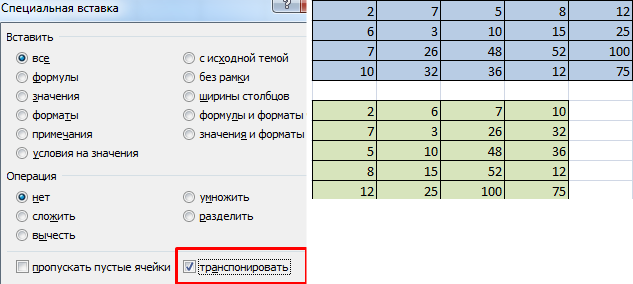
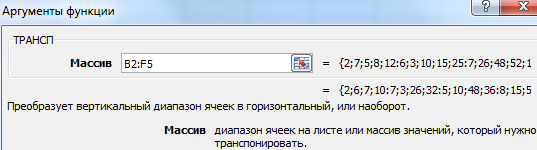
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

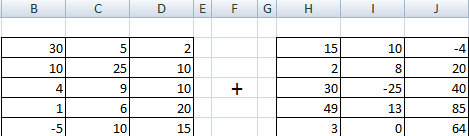
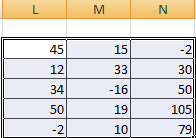
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Условие задачи:

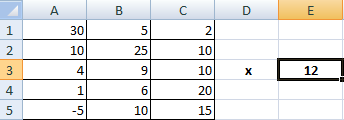
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

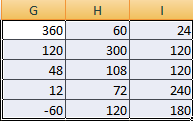
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

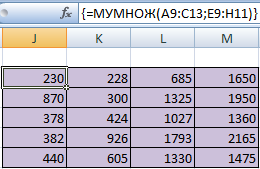
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

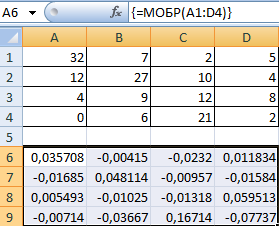
Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

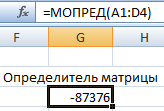
Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

РХТУ
им. Д.B.
Менделеева
Кафедра
ИКМ Методическое пособие по изучению
Excel

Операции
с матрицами в Excel

Как и над числами, над матрицами можно
проводить ряд операций, причем в случае
с матрицами некоторые из операций
являются специфическими.

1. Транспонирование.

Транспонированной называется матрица
(A^T), в которой столбцы исходной
матрицы (А) заменяются строками с
соответствующими номерами.

Пример. Пусть в диапазон ячеек А1:Е2
введена матрица размера 2 x
5. Необходимо получить транспонированную
матрицу.

• Выделить указателем мыши при нажатой
  левой кнопке блок ячеек, где будет
  находиться транспонированная матрица.
  В нашем примере блок размера 5 x
  2 в диапазоне А4:В8.

• Нажать на панели инструментов Стандартная
   вставка
  функции.

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категория
  выбрать Ссылки и массивы, а в рабочем
  поле Функция – имя функции ТРАСП
  (рис.1)

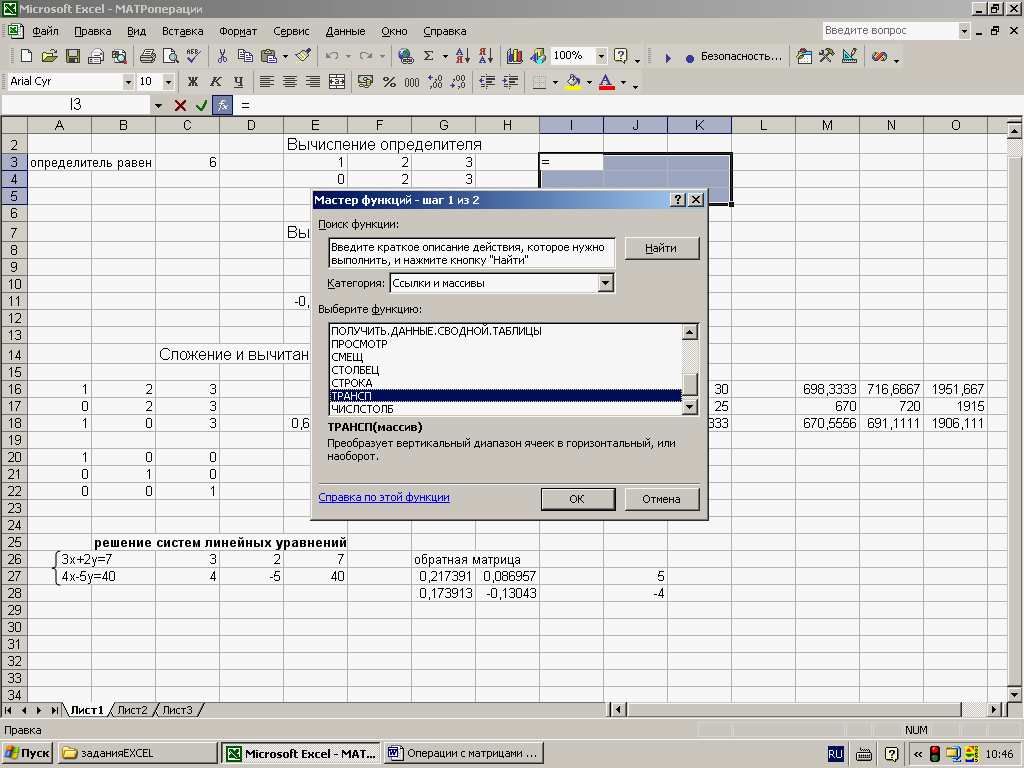
рис.1

• Появившееся диалоговое окно ТРАСП
  мышью отодвинуть в сторону от исходной
  матрицы и ввести диапазон исходной
  матрицы А1:Е2 в рабочее поле Массив
  (указателем мыши при нажатой левой
  кнопке). После чего, не нажимая кнопку
  ОК, нажать сочетание клавиш CTRL+SHIFT+ENTER
  (рис.2)

• Если транспонированная матрица не
  появилась в заданном диапазоне А4:В8,
  то надо щелкнуть указателем мыши в
  строке формул и повторить нажатие
  клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне А4:В8 появится
транспонированная матрица.

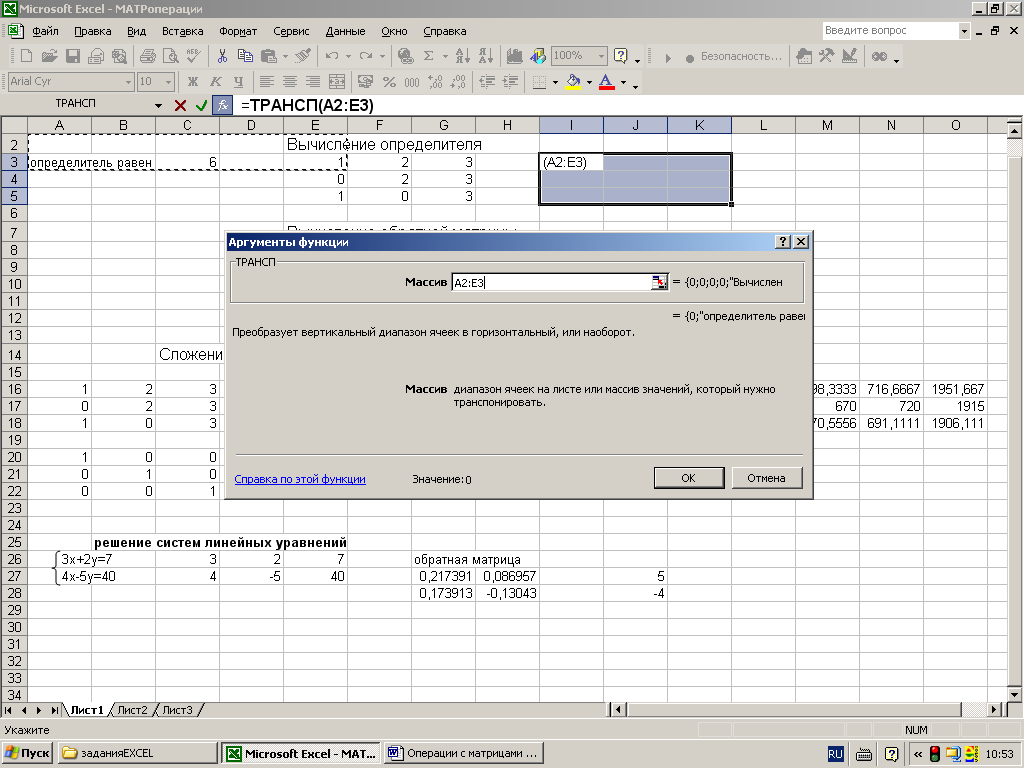
Рис.2

1. Вычисление определителя матрицы

Пусть в диапазон А1:С3 введена матрица.
Необходимо вычислить определитель
матрицы

• Табличный курсор поставить в ячейку,
  в которой требуется получить значение
  определителя, например. В А4.

• Нажать на панели инструментов Стандартная
  кнопку Вставка функции

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категории
  выбрать Математические, а в рабочем
  поле Функция – имя функции МОПРЕД.
  После этого нажать на кнопку ОК.

• Появившееся диалоговое окно МОПРЕД
  мышью отодвинуть в сторону от исходной
  матрицы и ввести диапазон исходной
  матрицы А1:С3 в рабочее поле Массив
  (указателем мыши при нажатой левой
  кнопке). После чего нажать кнопку ОК.

В ячейке А4 появится значение определителя
матрицы.

1. Нахождение обратной матрицы

Пусть в диапазон А1:С3 введена матрица.
Необходимо в диапазоне А5:С7 получить
обратную матрицу.

• Выделить блок ячеек под обратную
  матрицу (в нашем примере А5:С7)

• Нажать на панели инструментов Стандартная
  кнопку Вставка функции

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категории
  выбрать Математические, а в рабочем
  поле Функция – имя функции МОБР.
  После этого нажать на кнопку ОК.

• Появившееся диалоговое окно МОБР мышью
  отодвинуть в сторону от исходной
  матрицы и ввести диапазон исходной
  матрицы А1:С3 в рабочее поле Массив
  (указателем мыши при нажатой левой
  кнопке). После чего, не нажимая кнопку
  ОК, нажать сочетание клавиш CTRL+SHIFT+ENTER

• Если обратная матрица не появилась в
  заданном диапазоне А1:С3, то надо щелкнуть
  указателем мыши в строке формул и
  повторить нажатие клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне А1:С3 появится
обратная матрица.

1. Сложение и вычитание матриц, умножение
   и деление матрицы на число

Складывать (вычитать) матрицы можно
одного размера. В Excel для
выполнения операция сложения (вычитания)
матриц используются формулы, вводимые
в соответствующие ячейки.

Пример. Пусть матрица А введена в диапазон
А1:С2, а матрица В – в диапазон А4:С5.
Необходимо найти матрицу С, являющуюся
их суммой, в диапазоне Е1:G2.

С = А + В

• Табличный курсор установить в левый
  верхний угол результирующей матрицы
  – ячейку Е1.

• Ввести формулу для вычисления первого
  элемента результирующей матрицы =А1+А4
  (предварительно установить английскую
  раскладку клавиатуры)

• Скопируйте введенную формулу в остальные
  ячейки результирующей матрицы.

В результате в ячейках E1:G2
появится матрица, равная сумме исходных
матриц.

Подобным образом вычисляется разность
матриц, только в формуле вместо знака
+, ставится знак -.

Если необходимо умножить (разделить)
матрицу А на число k, то
формула будет иметь вид =А1*k.

Рис.3

Умножение матриц

Произведение двух матриц определено,
если число столбцов первой матрицы
произведения равно числу строк второй
матрицы произведения.

Пример. Пусть матрица введена в
диапазон A1:D3,
а матрица В – в диапазон А4:В7. Необходимо
найти произведение этих матриц С=А x
В.

• Выделить блок ячеек указателем мыши
  при нажатой левой кнопке под результирующую
  матрицу. Если матрица А имеет размерность
  3 x 4, а матрица В
  имеет размерность 4
  x 3, то результирующая матрица С
  имеет размерность 3
  x 3. Поэтому следует внимательно
  следить, чтобы размерность матрицы С
  в точности соответствовала определению
  произведения двух матриц. Пусть матрица
  С будет размещаться в диапазоне F1:G3.

• Нажать на панели инструментов Стандартная
  кнопку Вставка функции

• В появившемся диалоговом окне Мастер
  функций в рабочем поле Категории
  выбрать Математические, а в рабочем
  поле Функция – имя функции МУМНОЖ.
  После этого нажать на кнопку ОК.

• Появившееся диалоговое окно МУМНОЖ
  мышью отодвинуть в сторону от исходной
  матрицы и ввести диапазон первой матрицы
  А1:D3 в рабочее поле Массив1
  (указателем мыши при нажатой левой
  кнопке), а диапазон матрицы В – А4:В7
  ввести в рабочее поле Массив2. После
  чего, не нажимая кнопку ОК, нажать
  сочетание клавиш CTRL+SHIFT+ENTER
  (рис.3)

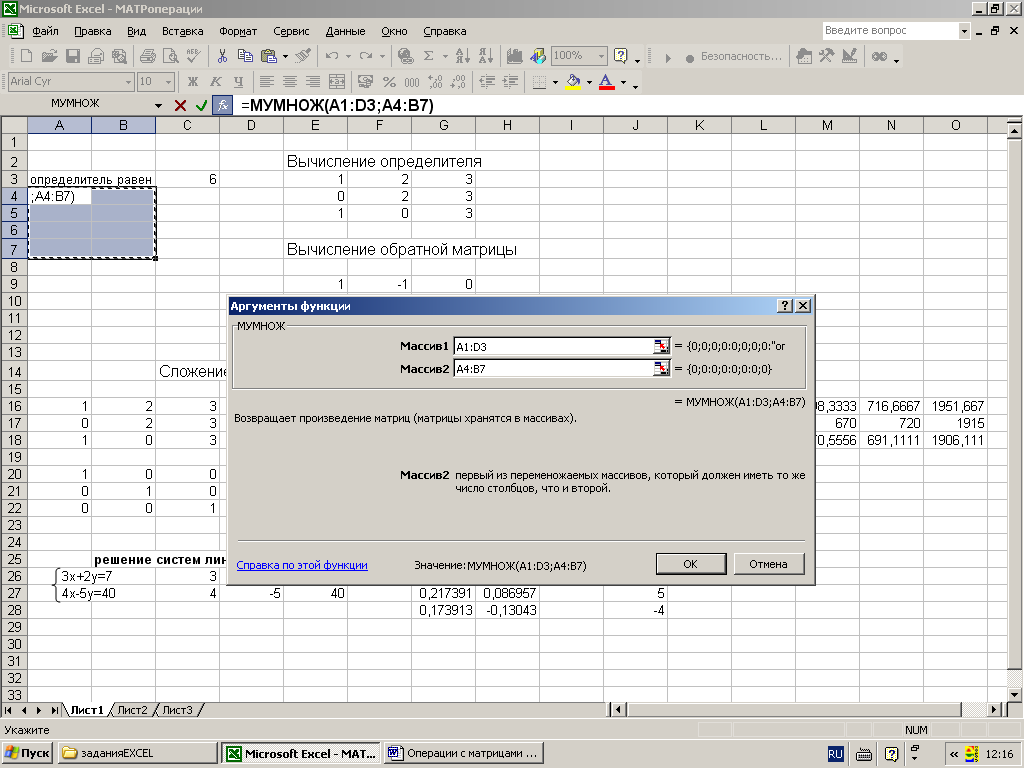
Рис.4

• Если произведение матриц не появилось
  в заданном диапазоне А1:С3, то надо
  щелкнуть указателем мыши в строке
  формул и повторить нажатие клавиш
  CTRL+SHIFT+ENTER.

В результате в диапазоне F1:G3
появится обратная матрица.

Соседние файлы в папке Excel

• #
• #
• #

  08.01.201420.99 Кб114Excel-таблицы-простые.xls

• #
• #
• #