План урока:
Сложение отрицательных чисел
Сложение чисел с разными знаками
Вычитание отрицательных чисел и чисел с разными знаками
В субботу, ученики 6 класса договорились встретиться и погулять в парке. Утром Юля выглянула в окошко, ярко светит солнышко, но при этом морозно. Девочка взглянула на термометр. Он показывал -10˚C. Мама попросила Юлю пойти на улицу немного позже, когда на улице потеплеет. Юля расстроилась и стала ждать. Через два часа девочка снова взглянула на термометр. Он показал -3. Ого! Всего два часа, а так потеплело – обрадовалась девочка и стала одеваться, чтобы идти гулять. В это время в комнату вошла мама и удивленно спросила «Уже потеплело? На сколько градусов?» Дочь не знала, что сказать и как правильно узнать, на сколько градусов стало теплее. Мама пришла на помощь и сообщила, что достаточно от -10 отнять -3, и мы узнаем, на сколько градусов изменилась температура воздуха за окном. Иначе, можно сказать, что шкала термометра поднялась вверх на 7 делений, значит, на улице стало теплее на 7 градусов. Запомнив все, что рассказала мама, Юля побежала в парк делиться новыми знаниями с друзьями.
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
В театре Карабаса-Барабаса актерам жилось очень сложно, все куклы мечтали жить на свободе. Актеры тяжело работали, но долги перед хозяином росли с каждым днем. Злой владелец пообещал отпустить Буратино и Мальвину из своего театра только тогда, когда кукольные герои вернут ему долг. Сколько монет нужно собрать героям, чтобы оказаться на свободе, если у Буратино было -15 монет, а у Мальвины -6?

Чтобы ответить на главный вопрос задачи, нам нужно понимать, о чем идет речь. Изучив условие, возникает вопрос «Как может быть -15 и -6 монет?». В данном случае выходит, что Буратино и Мальвина должны вернуть Карабасу-Барабасу 15 и 6 монет, поэтому перед данными числами и стоит знак «минус». Получается, кукольные персонажи смогут покинуть театр, когда полностью вернут долг. Для этого необходимо узнать общий размер долга Буратино и Мальвины. Чтобы узнать размер долга, суммируем монеты персонажей -15 и -6. Но как их сложить, когда перед слагаемыми стоит «минус»? В подобных ситуациях применяют правило сложения отрицательных чисел.

Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.

Получается, что герои имеют -21 монету, следовательно, они должны собрать 21 монету и вернуть долг, только тогда появится возможность покинуть театр Карабаса-Барабаса.

Источник
Рассмотрим еще одно задание.
Найдите результат сложения -24 и -16.
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
-24+(-16)=-(24+16)=-40.
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Рассмотрим ситуацию.
Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?
Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
- определяем модули: -3=|3|, 10=|10|;
- сравниваем модули, определяя больший: |3|<|10|;
- от большего отнимаем меньший: 10 – 3=7;
- так как по условию 10 – число положительное, то и результат будет числом положительным.
Записывается в таком виде:
-3+10=10 – 3=7.
Выходит, у мальчика стало 7 яблок.

Рассмотрим еще один пример сложения чисел с разными знаками.
Вычислите сумму -28 и 11.
Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.
-28=|28|;
11=|11|;
28>11.
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
-28+11=-(28-11)=-17.
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
-150+50=-(150-50)=-100.
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150=|150|;
-100=|100|.
150>100;
-150<-100.
Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.
Вычитание отрицательных чисел и чисел с разными знаками
Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:
Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.
Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.
Определите, чему будет равно значение выражения: от -510 отнять +210.
На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:
-510-(+210)
Сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:
Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.
Например: -5-(+2).
Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).
По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:
-5+(-2)=-(5+2)=-7
Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:
Запишем выражение:
-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:
-510-(+210)=-510+(-210)=-(510+210)=-720.
Вычисления окончены.

Источник
Рассмотрим следующее задание.
Найдите значение выражения: -248+248.
Используем правило сложения значений с разными знаками.
-248=|248|;
248=|248|;
248 – 248=0.
Следовательно, при сложении противоположных числовых значений в результате всегда будет 0.
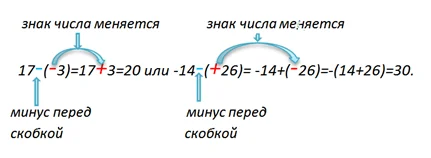
Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.
К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.
Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».
Вычисли: -36+(-7).
В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.
В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.
Минутка истории
История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.
Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом .
Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.
Вам известно, что существуют как положительные, так и отрицательные числа. Уроками ранее вы научились выполнять с положительными и отрицательными числами различные действия: определять и отмечать их на координатной прямой, находить модуль, сравнивать и складывать с помощью координатной прямой.
Операция сложения положительных чисел нам знакома уже давно.
Сегодня на уроке постараемся выяснить, возможно ли складывать отрицательные числа друг с другом и что будет результатом такого сложения.
Эта информация доступна зарегистрированным пользователям
Рассмотрим правило сложения отрицательных чисел и выясним, как изображают сумму отрицательных чисел на координатной прямой.
Разберем примеры сложения отрицательных чисел.
Использование отрицательных чисел в настоящее время обычно и естественно, но такая ситуация была не всегда.
Древние вообще не пользовались отрицательными числами, считали их недопустимыми, относились к ним настороженно, существование их долгое время отрицали и все полученные отрицательные результаты вычислений считали недействительными и абсурдными.
Интересен тот факт, что осознание существования и нужности отрицательных чисел началось с представления и применения их в торговле в качестве «долга» и «убытка».
Положительные числа трактовали как «прибыль» и «имущество».
Индийский математик и астроном Брахмагупта сформулировал правила сложения и вычитания отрицательных чисел, в которых говорилось:
«Сумма двух имуществ есть имущество»
(+х) + (+х) = +Х
«Сумма двух долгов есть долг»
(-х) + (-х) = -Х
Таким образом, если воспринимать отрицательные числа как «долг», то в таком случае модуль отрицательного числа будет являться величиной этого долга.
Задача:
Землевладелец попросил у своего знакомого в долг 4 мешка зерна для весеннего посева, но четырех мешков ему не хватило, и он попросил в долг еще 2 мешка зерна.
Эта информация доступна зарегистрированным пользователям
Сколько мешков зерна остался должен в итоге землевладелец своему знакомому?
Решение:
Четыре мешка зерна были взяты в долг, значит, число 4 будет обозначено отрицательным числом (-4).
Два мешка зерна так же были взяты в долг, значит, число 2 тоже будет со знаком минус (-2).
Необходимо найти общее количество мешков, взятых в долг, т.е. сумму отрицательных чисел –4 и –2.
Сумму двух отрицательных чисел можно записать двумя способами:
1. -4 + (-2) = -6
Знаки, стоящие рядом, отделяют друг от друга скобкой.
2. -4 – 2 = -6
Часто скобки и знак плюс опускают, при этом запись суммы отрицательных чисел становится короче, но она равнозначна первой записи (т.е. прибавление отрицательного числа равносильно вычитанию положительного).
Итак, мы выяснили, что долг землевладельца возрос и он составил 6 мешков зерна.
Мы можем заметить, что в результате сложения двух долгов, двух отрицательных чисел –4 и –2, получается долг (отрицательное число).
Сформулируем общее правило сложения отрицательных чисел.
Эта информация доступна зарегистрированным пользователям
Чтобы сложить отрицательные числа, нужно:
1. Сложить модули отрицательных чисел
2. Поставить перед полученным числом знак минус «-»
В буквенном виде правило выглядит так:
(-а) + (-b) = -(a + b) или -a – b = -(a + b)
Эта информация доступна зарегистрированным пользователям
Рассмотрим еще несколько примеров жизненных задач, где применяется сложение отрицательных чисел.
Задача:
Игрок набрал 6 штрафных очков за первую половину турнира, затем под конец турнира совершил еще одно нарушение. Судья назначил игроку 1 штрафное очко.
Сколько штрафных очков получил игрок за весь турнир?
Решение:
Штрафные очки можно записать отрицательным числом:
-6 – штрафные очки за первую половину турнира.
-1 – штрафное очко за вторую половину турнира.
Чтобы получить общее количество штрафных очков, нужно сложить все штрафы за турнир.
Воспользуемся правилом сложения отрицательных чисел.
Найдем модули отрицательных чисел:
|-6| = 6
|-1| = 1
Выполним сложение модулей чисел
6 + 1 = 7
Поставим знак минус перед полученным числом, получим (-7)
Решение задачи выглядит так:
–6 + (-1) = -(6 + 1) = -7
Ответ: 7 штрафных очков получил игрок за турнир.
Задача:
Рассмотрим задачу о понижении температуры воздуха.
Эта информация доступна зарегистрированным пользователям
Температура воздуха в полдень была –3ºС, а к вечеру она понизилась на 5ºС. Какая температура воздуха стала вечером?
Решение:
Воспользуемся правилом сложения отрицательных чисел.
–3 – температура воздуха в полдень.
–5 – понижение температуры на 5ºС
Найдем модули отрицательных чисел:
|-3| = 3
|-5| = 5
Выполним сложение модулей чисел
3 + 5 = 8
Поставим знак минус перед полученным числом, получим (-8)
Запись решения задачи выглядит так:
–3 + (-5) = -(3 + 5) = -8ºС
Ответ: температура воздуха стала вечером равной –8ºС
Эта информация доступна зарегистрированным пользователям
Сложение отрицательных чисел, небольших по модулю, легко представить на координатной прямой.
Рассмотрим сложение отрицательных чисел с помощью координатной прямой на примере задачи о понижении температуры воздуха, рассмотренной выше.
Мы уже знаем из условий задачи, что
–3ºС – температура воздуха в полдень.
–5ºС – понижение температуры к вечеру на 5ºС (т.е. изменение температуры составляет –5ºС).
Для задачи изобразим координатную прямую, направленную вправо, с точкой О (0) – точкой начала отсчета и с единичным отрезком, в котором 1 деление = 1ºС
По направлению координатной прямой откладываются положительные значения.
Против направления координатной прямой откладываются отрицательные значения.
Эта информация доступна зарегистрированным пользователям
Отметим на координатной прямой начальную температуру воздуха. Она равна –3ºС, значит, от точки О (0) влево откладываем 3 единичных отрезка, попадаем в точку А (-3)
Понижение температуры на 5ºС, т.е. прибавление числа –5 (или вычитание числа 5), означает сдвиг точки А (–3) влево на 5 единичных отрезков – попадаем в точку В (-8)
Температура воздуха к вечеру стала равной –8ºС
А это значит:
–3 + (-5) = –3–5 = –(|-3| + |-5|)= –8ºС
Рассмотрим порядок сложения двух отрицательных чисел с помощью координатной прямой:
1. Отметить на координатной прямой точку, с координатой равной первому слагаемому
2. Переместить ее против направления координатной прямой на расстояние (количество единичных отрезков), равное модулю следующего слагаемого
3. Полученная точка на координатной прямой будет иметь значение, равное сумме отрицательных чисел
Если суммируется не два отрицательных числа, а больше, то после п.3 рассмотренного порядка сложения отрицательных чисел с помощью координатной прямой, необходимо применить п.2 для каждого следующего слагаемого.
Пример:
–2 + (-2) + (-3) = –4 + (-3) = –7
Изобразим координатную прямую, направленную вправо, с точкой О (0) – точкой начала отсчета и с единичным отрезком, равным 1 деление = 1 единица.

Попробуем разобраться с помощью координатной прямой в истинности утверждений:
- Любое число от прибавления отрицательного числа уменьшается
- При сложении отрицательных чисел всегда получатся отрицательное число
- Модуль суммы отрицательных чисел равен сумме модулей слагаемых
Доказательство первого утверждения:
Так как слагаемые отрицательные числа, то точки, соответствующие этим числам, находятся слева от точки начала отсчета.
В результате сложения отрицательных слагаемых точка перемещается еще дальше от точки начала отсчета влево (против направления координатной прямой), что говорит об уменьшение значения суммы и о том, что значение суммы будет являться отрицательным числом.
Доказательство второго утверждения:
Отмечая точку, соответствующую первому слагаемому, откладываем влево от начала координат (против направления координатной прямой) отрезок, длина которого равна модулю этого слагаемого. В результате полученная точка смещается влево (против направления координатной прямой) на отрезок, равный модулю следующего слагаемого и т.д. Следовательно, сумма длин отрезков (а это значит, сумма модулей слагаемых) равняется модулю суммы всех слагаемых.
Пример:
–2+(-2)+(-3)+(-3) = –10
Изобразим координатную прямую направленную вправо с точкой О (0) – точкой начала отсчета и с единичным отрезком равным 1 деление = 1 единица.
Эта информация доступна зарегистрированным пользователям
OA = 2 – модуль первого слагаемого
AB = 2 – модуль второго слагаемого
BC = 3 – модуль третьего слагаемого
CD = 3 – модуль четвертого слагаемого
OD = 10 – модуль суммы всех слагаемых
OD = OA + AB + BC + CD = 2 + 2 + 3 + 3= 10
Эта информация доступна зарегистрированным пользователям
Разберем несколько примеров сложения отрицательных чисел.
Задача 1
Найдите значение выражения –120 + (-1610)
Решение:
Воспользуемся правилом сложения отрицательных чисел.
Найдем модули данных чисел:
|-120| = 120
|-1610| = 1610
Выполним сложение модулей чисел:
120 + 1610 = 1730
Поставим знак минус перед полученным числом, получим –1730
Краткий вид решения выглядит так:
-120 + (-1610) = -(120 + 1610) = -1730
Ответ: -1730
Заметим, что при перестановке слагаемых местами сумма отрицательных чисел не изменится.
-120 + (-1610) = -120 – 1610 = -(120 + 1610) = -1730
Слагаемые переставим местами – значение суммы не изменилось:
-1610 + (-120) = -1610 – 120 = -(1610 + 120) = -1730
Задача 2
Сложите отрицательные числа (mathbf{-frac{1}{2}}) и –6,5
При сложении отрицательных рациональных чисел их необходимо привести к общему виду.
Решение:
Согласно правилу сложения отрицательных чисел, первым делом определим модули отрицательных чисел:
(mathbf{|-frac{1}{2}| = frac{1}{2}})
|-6,5| = 6, 5
Выполним сложение модулей чисел, предварительно приведем числа к общему виду.
Значения удобно свести к десятичным дробям:
(mathbf{frac{1}{2} = 0,5})
0,5+6,5 = 7
Поставим знак минус перед полученным значением, получим –7
Краткий вид решения выглядит так:
(mathbf{-frac{1}{2}}) + (-6,5) = -((mathbf{frac{1}{2}}) + 6,5) = -(0,5 + 6,5) = -7
Ответ: -7
Задача 3
Найдите значение выражения a+ b+ c, если
a = –16
b = –3,5
c = (mathbf{-frac{1}{5}})
Решение:
При сложении получаем выражение вида: –16+(-3,5)+( (mathbf{-frac{1}{5}}))
Согласно правилу сложения отрицательных чисел, определим модули отрицательных чисел:
|-16| = 16
|-3,5| = 3,5
(mathbf{|-frac{1}{5}| = frac{1}{5} = 0,2})
Выполним сложение модулей чисел:
16 + 3,5 + 0,2 = 19,7
Перед полученным числом поставим знак минус, получим –19,7
Краткий вид решения выглядит так:
-16 + (-3,5) + ( (mathbf{-frac{1}{5}}))= -(16 + 3,5 + (mathbf{frac{1}{5}})) = -(16 + 3,5 + 0,2) = -19,7
Ответ: -19,7
Задача 4
Решите уравнение х + 3 = -14
Решение:
Решение данного уравнения сводится к нахождению неизвестного слагаемого.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Согласно правилу сложения отрицательных чисел, определим сумму отрицательных чисел:
х = -14 + (-3)
х = -(14 + 3)
х = -17
Ответ: -17
Эта информация доступна зарегистрированным пользователям
Читайте также
|
Отрицательные числа складываются точно так же как и положительные. При этом знак “минус” сохраняется. Пример. -2+ (-2)= -2-2 (открыли скобки)=-4. К сожалению автор под ником Darli ing ошибся. При сложении и вычитании знак “минус” сохраняется. Знак “минус” переходит в “плюс” только при умножении или делении отрицательных чисел друг на друга. автор вопроса выбрал этот ответ лучшим
Степан-16 5 лет назад Если два числа имеют одинаковый знак: “плюс” или “минус”, то они складываются, а результат будет иметь тот же знак, что и суммируемый числа. То есть, вначале сложили, записали результат, проставили знак.
SIRINA 8 лет назад Для сложения двух отрицательных чисел необходимо сложить их модули, то есть число без знака “минус”. В итоге получается сумма двух чисел, но перед суммой нужно поставить знак “минус”. Например:-2 -2=(-2)+(-2)=-(2+2)=-4. Существует даже правило сложения отрицательных чисел −a и −b в виде: (−a)+(−b)=−(a+b).
Понять принципы сложения отрицательных чисел сложно потому, что в обыденной жизни мы никогда не сталкиваемся с минус одним яблоком или минус пятеркой за ответ на уроке, то есть отрицательные числа для большинства столь же абстрактны, как и мнимые. Хотя вот бухгалтера любят иметь дело с отрицательными числами и выводить их в плюс. При сложении этих чисел следует помнить, что минус никуда не денется. Проще всего сложить такие числа как обычные положительные числа, а потом просто добавить перед суммой минус, то есть складывать модули чисел: -|2+4|=-6 Точно также следует поступать и при вычитании таких чисел, причем если результат вычитания модулей окажется отрицательным, то добавленный минус сделает его положительным: -|2-4|=-(-2)=2
Ксарфакс 5 лет назад Предположим, у нас имеются два отрицательных числа a и b. a = – 5. b = – 10. Сумма отрицательных чисел = a + b = -5 + (-10) = -5 – 10 = -(5+10) = -15. Таким образом, становится понятно, что для сложения нескольких отрицательных чисел нужно сложить их модули, а затем к результату приписать знак минус: -a + (-b) = -(|a|+|b|). Просто достаточно помнить, что при суммировании двух отрицательных чисел мы всегда получаем ещё большее уменьшение (сумма будет находится на числовой оси левее обоих слагаемых).
Skiyers 8 лет назад На миг забудьте о том, что перед цифрами стоят минусы и сплюсуйте их. А потом вспоминайте и к результату добавьте минус. Например, если сложить -5 и -3, то получится -8. А вот если к отрицательному числу надо добавить положительное (пример -2+4), то просто поменяйте их местами (+4-2), и вы поймете, что ответом будет 2.
Galina7v7 6 лет назад Для сложения двух ( и более) отрицательных чисел нужно, не обращая внимания на знаки минус сложить модули (значения без знака минус), и к результату ” приписать знак минус.Для примера : -115 – 97 = -( 115 + 97) = – 212. -3 -4 -5 =-(3+4+5) = -12 И более простой пример: -1 -3 =-(1 +3)=-4
Olbast 8 лет назад Сложение отрицательных чисел происходит точно также как и положительных. Складываете цифры, а перед полученным результатом ставите знак “-“. Пример: -4 + (-6)= -10. Это правило действует только для сложения. В случае умножения: “-” * “-” = +; В случае деления: “-“/”-“= +.
Алиса в Стране 5 лет назад Если оба ваши числа отрицательные, то при сложении можно просто забыть о минусах, стоящих перед ними, сложите эти числа так, как будто бы они были положительными, но потом перед суммой поставьте знак минус. -132 + (-68), это все равно что -(132 + 68) = -200
Azamatik 5 лет назад Если нужно сложить два числа с отрицательным знаком, знак [–] выносится за скобки, а числа складываются. Отрицательный знак сохраняется. Итак, примеры: Нужно сложить -32 и -48. -32 + (-48) = – (32 + 48) = – 80. Второй пример: -10 + (-60) = – (10+60) = – 70. Знаете ответ? |
В этом материале мы расскажем, как правильно выполнять сложение отрицательного и положительного числа. Сначала мы приведем основное правило такого сложения, а потом покажем, как оно применяется при решении задач.
Основное правило сложения положительных и отрицательных чисел
Мы уже говорили ранее, что положительное число можно рассматривать как доход, а отрицательное – как убыток. Чтобы узнать величину дохода и расхода, надо смотреть на модули этих чисел. Если в итоге окажется, что наши расходы превышают доходы, то после их взаимного учета мы останемся должны, а если наоборот, то мы останемся в плюсе. Если же расходы равны доходам, то у нас будет нулевой остаток.
Используя приведенные выше рассуждения, можно вывести основное правило сложения чисел с разными знаками.
Для сложения положительного числа с отрицательным необходимо найти их модули и выполнить сравнение. Если значения окажутся равны, то мы имеем два слагаемых, которые являются противоположными числами, и их сумма будет нулевой. Если же они не равны, то нам надо учесть, что результат будет иметь тот же знак, что и большее число.
Таким образом, сложение в данном случае сводится к вычитанию из большего числа меньшего. Итог этого действия может быть разным: мы можем получить как положительное, так и отрицательное число. Нулевой результат тоже возможен.
Это правило распространяется на целые, рациональные и действительные числа.
Задачи на сложение положительного числа с отрицательным
Разберем, как применять на практике правило, озвученное выше. Возьмем для начала простой пример.
Вычислите сумму 2+(-5).
Решение
Выполним последовательно шаги, которые мы изучили до этого. Найдем для начала модули исходных чисел, которые будут равны 2 и 5. Больший модуль – 5, поэтому запоминаем минус. Далее вычитаем из большего модуля меньший и получаем: 5−2=3.
Ответ: (−5)+2=−3.
Если в условиях задачи стоят рациональные числа с разными знаками, не являющиеся при этом целыми, то для удобства расчетов нужно представить их в виде десятичных или обыкновенных дробей. Возьмем такую задачу и решим ее.
Вычислите, сколько будет 218+(-1,25).
Решение
Первым делом переведем смешанное число в обыкновенную дробь. Если вы не помните, как это делается, перечитайте соответствующую статью.
218=178
Десятичную дробь мы тоже представим в виде обыкновенной: -1,25=-125100=-54.
После этого уже можно переходить к вычислению модулей и подсчету результата. Найдем модули: они будут равны 178 и 54 соответственно. Получившиеся дроби приведем к общему знаменателю и получим 178 и 108.
Следующим шагом будет сравнение обыкновенных дробей. Поскольку числитель первой дроби больше, то 178>108. Если слагаемое со знаком плюс у нас больше, то нам надо запомнить, что результат будет положительным.
Далее вычтем из большего модуля меньший (см. материал о том, как найти разность дробей с одинаковыми знаменателями):
178-108=17-108=78
Мы уже отмечали ранее, что результат у нас будет со знаком плюс: +78. Так как плюс писать необязательно, при записи ответа обойдемся без него.
Запишем весь ход решения:
218+-1,25=178+-54=178+-108=178-108=78
Ответ: 218+-1,25=78.
Найдите, чему будет равна сумма 14 и -14.
Решение
Мы имеем два одинаковых слагаемых с разными знаками. Значит, эти числа являются противоположными друг другу, следовательно, их сумма будет равна 0.
Ответ: 14+-14=0
В конце статьи добавим, что результат сложения действительных отрицательных чисел с положительными зачастую лучше записывать в виде числового выражения с корнями, степенями или логарифмами, а не в виде бесконечной десятичной дроби. Так, если мы сложим числа n и -3, то ответ будет равен n-3. Считать окончательный результат нужно далеко не всегда, и можно обойтись приблизительными расчетами. Более подробно об этом мы напишем в статье об основных действиях с действительными числами.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
![]()
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Вот смотри…
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Определение модуля:
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)
Свойства модуля:
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
![]()
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
![]()
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
![]()
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
![]()
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
![]()
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
( |mathbf{a}|,) (( a) — любое число).
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf{3} right|=mathbf{3})
( left| -mathbf{3} right|=mathbf{3}.)
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)
( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)
А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)
( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| text{ }le text{ } right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10}) | ( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Выражения также равны, если оба числа отрицательны:
| ( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10) | ( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4}) | ( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
или
| ( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4}) | ( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
( mathbf{4}<mathbf{10})
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
( {{left| x right|}^{2}}=?)
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
( {{left| x right|}^{2}}={{x}^{2}})
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
( {{left| 5 right|}^{2}}={{5}^{2}}=25)
( {{left| -5 right|}^{2}}=?)
Ну, и почему сомнения? Действуем смело!
( {{left| -5 right|}^{2}}={{5}^{2}}=25)
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
а) ( |3|text{ }+text{ }|-9|;)
б) ( |-5|text{ }-text{ }|6|;)
в) ( |15left| cdot right|-3|;)
г) ( displaystyle frac{|8|}{|-2|}).
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:
( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
![]()
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)
Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).
Решение:
( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)
( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)
( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb{R}):
- ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при text{ }c>0)
- ( {{left| x right|}^{2}}={{x}^{2}})
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Подготовка к ЕГЭ на 90+ в мини-группах
![]()
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
