Как найти сумму моментов всех сил – Сайт, где вы сможете решить свои вопросы

Рассмотрим решение задачи по составлению и определению суммы моментов внешних сил приложенных к заданной системе относительно её точек.

Задача
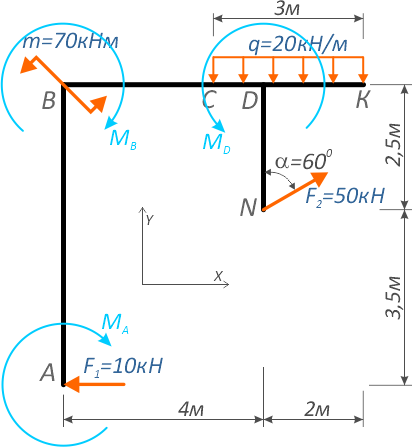
К составной планке, показанной на рисунке

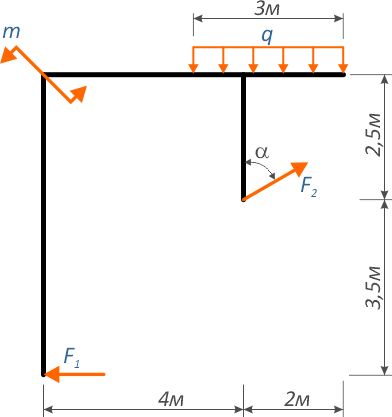
Заданная схема для составления суммы моментов

приложены следующие нагрузки:

Внешние сосредоточенные силы F₁=10кН и F₂=50кН расположенная под углом
Сосредоточенный момент m=70кНм
Равномерно-распределённая нагрузка q интенсивностью 20кН/м

Требуется составить и определить алгебраическую сумму моментов относительно точек A, B и D.

Решение

Обозначим характерные точки системы буквами и покажем систему координат x-y.

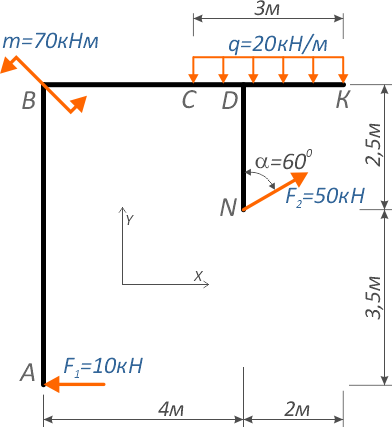
Система координат для расчета

Для записи и расчета уравнений суммы моментов надо мысленно закрепить систему в рассматриваемой точке и записать все внешние усилия, которые стремятся повернуть систему.

Момент силы определяется по формуле

где h — расстояние от точки до линии действия силы называемое плечом.

Другие видео

При этом, по правилу знаков, нагрузки, поворачивающие систему против хода часовой стрелки записываются положительными и наоборот.

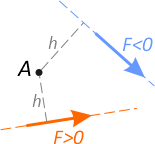
Знаки моментов

При записи уравнений суммы моментов:

Силы умножаются на плечо;
Равномерно распределенные нагрузки умножаются на длину (получается равнодействующая сила), полученное произведение умножается на плечо, которым служит расстояние от её середины до рассматриваемой точки;
Сосредоточенный момент в сумме моментов записывается как есть (с учётом знака).

Примеры составления суммы моментов сил

Определим алгебраические суммы моментов сил относительно произвольных точек системы.

Для некоторого упрощения решения задачи, распределенную нагрузку можно заменить её равнодействующей

которая при равномерном распределении приложена посередине:

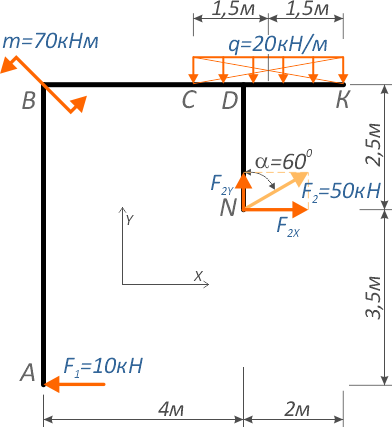
Положение равнодействующей нагрузки

а сосредоточенную силу F₂ можно разложить на составляющие, спроецировав её на оси x и y.

Проекции силы F на оси x и y

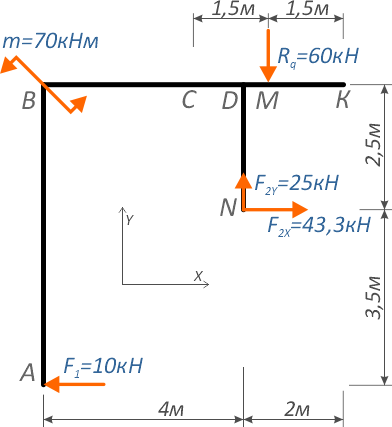
Получается упрощенная расчетная схема:

Упрощенная схема для расчета суммы моментов

Расчет суммы моментов относительно точки, к которой приложена сила

Для точки A:
Силы R_q и F_2X создают момент, вращающий по ходу часовой стрелки, поэтому будут записаны со знаком минус.
Сила F_2Y относительно точки A имеет обратное направление и создает положительный момент.

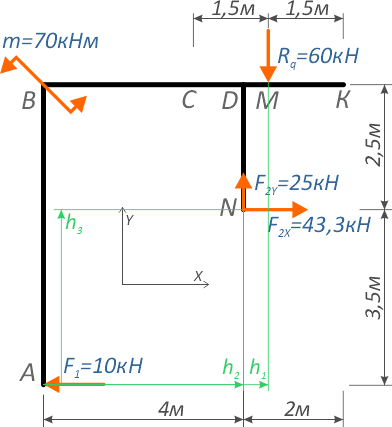
Определение суммы моментов относительно точки A

Здесь h₁, h₂ и h₃ плечи моментов соответствующих сил и равнодействующей распределенной нагрузки относительно точки A.

Линия действия силы F₁ проходит через саму точку A, следовательно, плечо равно нулю, поэтому момент этой силой в данном случае не создается.

Таким образом, относительно точки A уравнение суммы моментов будет иметь вид:

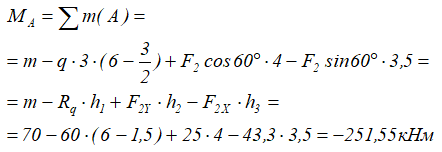
Уравнение суммы моментов относительно точки A

Здесь сумма моментов относительно точки A отрицательна, поэтому, если данную систему закрепить в этой точке, она будет вращаться по ходу часовой стрелки.

Определение суммы моментов относительно точки, в которой приложен момент

Для точки B надо помнить что момент приложенный в точке, относительно которой записывается сумма, в уравнении участвует.

Поэтому алгебраическая сумма моментов относительно точки B равна:

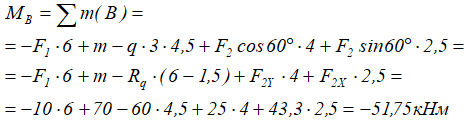
Алгебраическая сумма моментов относительно точки B

Знак «-» так же показывает на вращение системы по ХЧС.

Сумма моментов относительно точки, где действует распределенная нагрузка

Для точки D:
Здесь надо смотреть, как расположена равнодействующая нагрузки по отношению к рассматриваемой точке.
В данном случае она находится справа от точки и направлена вниз, следовательно, создает вращение по ходу часовой стрелки.

Плечом момента нагрузки служит расстояние между равнодействующей и точкой.

Уравнение суммы моментов для точки под распределенной нагрузкой (в точке D) запишется в виде:

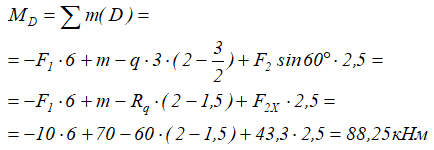
Определение суммы моментов в точке D

Положительный результат показывает вращение системы против ХЧС.

Направления определенных сумм моментов относительно заданных точек

Направления сумм моментов

При определении суммы моментов следует помнить, что в отличие от сил и распределенных нагрузок, сосредоточенный момент будет иметь один и тот же знак относительно любой точки системы.

Уравнения суммы моментов можно составить относительно любых других точек системы, в том числе точек, которые лежат вне заданной системы. Но, как правило, при решении задач этого не требуется.

Для статичных, геометрически неизменяемых систем сумма моментов всегда равна нулю.

Другие примеры решения задач статики >

Источник

iSopromat.ru

Правила знаков для моментов и проекций сил на оси координат:

Правило знаков проекций сил

То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.

Например, для такой схемы нагружения:

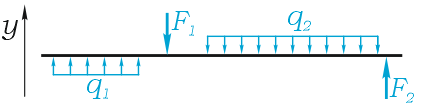
уравнение суммы сил имеет вид

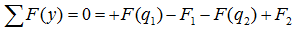
А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:

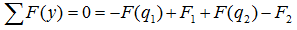
Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.

Правило знаков для моментов

Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

Например, для суммы моментов относительно точки A

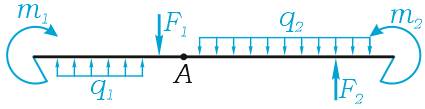
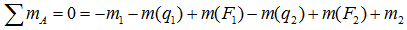
или, что одно и то же

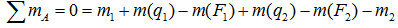
Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.

При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Момент силы и правило моментов

теория по физике 🧲 статика

Статика — раздел механики, изучающий условия равновесия тел.

Виды равновесия

Устойчивое равновесие

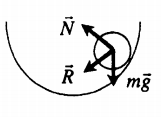
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (E_{p min}).

Неустойчивое равновесие

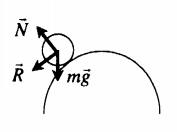
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (E_{p max}).

Безразличное равновесие

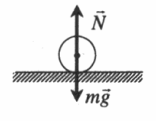
При выведении тела из положения безразличного равновесия дополнительных сил не возникает.

Момент силы

Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:

M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).

Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.

Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?

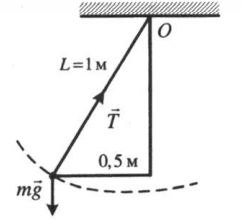
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:

Момент силы может быть положительным и отрицательным.

Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:

Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:

Правило моментов

Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

Иначе правило моментов можно сформулировать так:

Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.

∑ M п о ч а с . с т р . = ∑ M п р . ч а с . с т р .

Условия равновесия тел

∑ → F i = 0 ; → v o = 0

∑ → F i = 0 ; → v o = 0 и ∑ → F i = 0 ; → v o = 0

Простые механизмы

Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.

Наклонная плоскость

Тело не участвует в поступательном движении:
Тело не участвует во вращательном движении:
Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении)
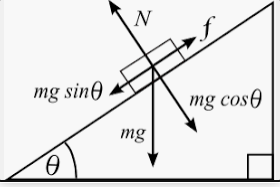	Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: Рычаг
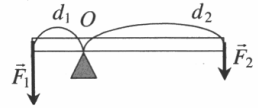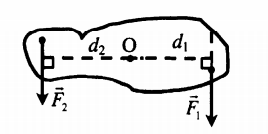
	Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F 1 F 2 . . = d 2 d 1 . . Неподвижный блок
	Изменяет направление действия силы. Модули и плечи сил при этом равны: Подвижный блок
	Дает выигрыш в силе в 2 раза:
	Делит силу на две равные части, направление которых зависит от формы клина:

Золотое правило механики

При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.

Алгоритм решения

Решение

Известна лишь масса батона: m₁ = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:

Запишем правило моментов:

Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:

Отсюда масса рыбы равна:

m 2 = m 1 d 1 d 2 . . = 0 , 8 · 0 , 3 0 , 4 . . = 0 , 6 ( к г )

pазбирался: Алиса Никитина | обсудить разбор | оценить

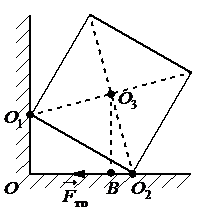Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения F → тр “> F _тр относительно оси, проходящей через точку О₃ перпендикулярно плоскости чертежа, равно.

Алгоритм решения

Сформулировать определение плеча силы.
Найти плечо силы трения и аргументировать ответ.

Решение

Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О₃В.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Теоретическая механика. В помощь студенту

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.

Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.

Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Статика твердого тела

Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.

Основные понятия и законы статики

Абсолютно твердое тело (твердое тело, тело) – это материальное тело, расстояние между любыми точками в котором не изменяется.

Материальная точка – это тело, размерами которого по условиям задачи можно пренебречь.

Свободное тело – это тело, на перемещение которого не наложено никаких ограничений.

Несвободное (связанное) тело – это тело, на перемещение которого наложены ограничения.

Связи – это тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).

Реакция связи — это сила, характеризующая действие связи на твердое тело. Если считать силу, с которой твердое тело действует на связь, действием, то реакция связи является противодействием. При этом сила — действие приложена к связи, а реакция связи приложена к твердому телу.

Механическая система – это совокупность взаимосвязанных между собой тел или материальных точек.

Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.

Сила – это векторная величина, характеризующая механическое действие одного материального тела на другое.
Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон.

Линия действия силы – это прямая, вдоль которой направлен вектор силы.

Сосредоточенная сила – сила, приложенная в одной точке.

Распределенные силы (распределенная нагрузка) – это силы, действующие на все точки объема, поверхности или длины тела.
Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).
Размерность распределенной нагрузки – Н/м 3 (Н/м 2 , Н/м).

Внешняя сила – это сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.

Внутренняя сила – это сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.

Система сил – это совокупность сил, действующих на механическую систему.

Плоская система сил – это система сил, линии действия которых лежат в одной плоскости.

Пространственная система сил – это система сил, линии действия которых не лежат в одной плоскости.

Система сходящихся сил – это система сил, линии действия которых пересекаются в одной точке.

Произвольная система сил – это система сил, линии действия которых не пересекаются в одной точке.

Эквивалентные системы сил – это такие системы сил, замена которых одна на другую не изменяет механического состояния тела.
Принятое обозначение:

Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.

Уравновешенная система сил – это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).

Равнодействующая сила – это сила, действие которой на тело эквивалентно действию системы сил.

Момент силы – это величина, характеризующая вращающую способность силы.

Пара сил – это система двух параллельных равных по модулю противоположно направленных сил.
Принятое обозначение:

.
Под действием пары сил тело будет совершать вращательное движение.

Проекция силы на ось – это отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси.
Проекция положительна, если направление отрезка совпадает с положительным направлением оси.

Проекция силы на плоскость – это вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости.

Закон 1 (закон инерции). Изолированная материальная точка находится в покое либо движется равномерно и прямолинейно.
Равномерное и прямолинейное движение материальной точки является движением по инерции. Под состоянием равновесия материальной точки и твердого тела понимают не только состояние покоя, но и движение по инерции. Для твердого тела существуют различные виды движения по инерции, например равномерное вращение твердого тела вокруг неподвижной оси.

Закон 2. Твердое тело находится в равновесии под действием двух сил только в том случае, если эти силы равны по модулю и направлены в противоположные стороны по общей линии действия.
Эти две силы называются уравновешивающимися.
Вообще силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в покое.

Закон 3. Не нарушая состояния (слово «состояние» здесь означает состояние движения или покоя) твердого тела, можно добавлять и отбрасывать уравновешивающиеся силы.
Следствие. Не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела.
Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела.

Закон 4. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой
диагонали.
По модулю равнодействующая равна:

Закон 5 (закон равенства действия и противодействия). Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны по одной прямой.
Следует иметь в виду, что действие — сила, приложенная к телу Б, и противодействие — сила, приложенная к телу А, не уравновешиваются, так как они приложены к разным телам.

Закон 6 (закон отвердевания). Равновесие нетвердого тела не нарушается при его затвердевании.
Не следует при этом забывать, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но недостаточными для соответствующего нетвердого тела.

Закон 7 (закон освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив действие связей соответствующими реакциями связей.

Связи и их реакции

Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.

Момент силы относительно точки

Абсолютное значение момента равно произведению модуля силы на кратчайшее расстояние h от центра вращения до линии действия силы. Расстояние h называют плечом силы.
Момент считают положительным, если сила стремится вращать плечо h против хода часовой стрелки и отрицательным при вращении по ходу часовой стрелки.
Свойства момента силы относительно точки:
1) Момент силы не изменится при переносе точки приложения силы вдоль линии действия силы.
2) Момент силы равен нулю, если линия действия силы проходит через точку приложения силы.
3) Момент равнодействующей силы относительно точки равен сумме моментов слагаемых сил относительно этой точки.
,
где

Момент силы относительно оси

Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
Чтобы найти момент силы относительно оси, нужно:
1) Провести плоскость перпендикулярную оси z.
2) Спроецировать силу на эту плоскость и вычислить величину проекции .
3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы и вычислить его длину.
4) Найти произведение этого плеча и проекции силы с соответствующим знаком.
Свойства момента силы относительно оси.
Момент силы относительно оси равен нулю, если:
1) , то есть сила параллельна оси.
2) h=0, то есть линия действия силы пересекает ось.

Момент пары сил

Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие)
,
где: — силы, составляющие пару;
h — плечо пары.
Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки.
Свойства пары сил.
1) Сумма проекций сил пары на любую ось равна нулю.
2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.
3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.

Преобразование сходящейся системы сил

Равнодействующая двух сходящихся сил находится на основании аксиомы о параллелограмме сил.
Геометрическая сумма любого числа сходящихся сил может быть определена путем последовательного сложения двух сил – способ векторного многоугольника.
Вывод: система сходящихся сил () приводится к одной равнодействующей силе .
Аналитически равнодействующая сила может быть определена через ее проекции на оси координат:
Согласно теореме: проекция равнодействующей на ось равна сумме проекций слагаемых сил на эту ось: , или в общем виде
С учетом равнодействующая определяется выражением:
.
Направление вектора равнодействующей определяется косинусами углов между вектором и осями x, y, z:

Преобразование произвольной системы сил

Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится.
В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом.
Суммарный вектор — это главный вектор системы сил.
Суммарный момент — это главный момент системы сил.
Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору и главному моменту системы сил.
Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат:
,

Условия равновесия систем сил

Равновесие системы сходящихся сил
Действие системы сходящихся сил эквивалентно действию одной равнодействующей силы.
Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю .
Из формулы следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю:
Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю:

Равновесие произвольной системы сил.

Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия:
.
Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю:
Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю:

Кинематика

Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.

Основные понятия кинематики

Закон движения точки (тела) – это зависимость положения точки (тела) в пространстве от времени.

Траектория точки – это геометрическое место положений точки в пространстве при ее движении.

Скорость точки (тела) – это характеристика изменения во времени положения точки (тела) в пространстве.

Ускорение точки (тела) – это характеристика изменения во времени скорости точки (тела).

Способы задания движения точки

Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
Закон движения: .
В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
Закон движения: x = x(t), y = y(t); z = z(t).
В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
Закон движения: .
Движение точки, при естественном способе задания движения, определено если известны:
1) Траектория движения.
2) Начало и направление отсчета дуговой координаты.
3) Уравнение движения.
При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
Главная нормаль (n) – направлена в сторону вогнутости кривой.
Бинормаль (b) – направлена перпендикулярно к осям τ, n.

Определение кинематических характеристик точки

Траектория точки
В векторной системе отсчета траектория описывается выражением: .
В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y) — в пространстве, или y = f(x) – в плоскости.
В естественной системе отсчета траектория задается заранее.
Определение скорости точки в векторной системе координат
При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: .
Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): .
Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
Вывод:скорость точки – векторная величина, равная производной от закона движения по времени.
Свойство производной:производная от какой либо величины по времени определяет скорость изменения этой величины.
Определение скорости точки в координатной системе отсчета
Скорости изменения координат точки:
.
Модуль полной скорости точки при прямоугольной системе координат будет равен:
.
Направление вектора скорости определяется косинусами направляющих углов:
,
где — углы между вектором скорости и осями координат.
Определение скорости точки в естественной системе отсчета
Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: .
Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .

Ускорение точки

По определению ускорение характеризует изменение скорости, то есть скорость изменения скорости.
Ускорения точки в векторной системе отсчета
На основании свойства производной:
.
Вектор скорости может изменяться по модулю и направлению.
Вектор ускорения направлен по линии приращения вектора скорости, т. е. в сторону искривления траектории.
Ускорение точки в координатной системе отсчета
Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат:
.
Полное ускорение в прямоугольной системе координат будет определяться выражением:
.
Направляющие косинусы вектора ускорения:
.
Ускорение точки в естественной системе отсчета Приращение вектора скорости можно разложить на составляющие, параллельные осям естественной системы координат:
.
Разделив левую и правую части равенства на dt, получим:
,
где — тангенциальное ускорение;
— нормальное ускорение;
R — радиус кривизны траектории в окрестности точки.

Кинематика твердого тела

В кинематике твердых тел решаются две основные задачи:
1) задание движения и определение кинематических характеристик тела в целом;
2) определение кинематических характеристик точек тела.
Поступательное движение твердого тела
Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
Теорема:при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
Вывод:поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
Вращательное движение твердого тела вокруг неподвижной оси
Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
Закон вращательного движения тела вокруг неподвижной оси .
Угловую скорость и угловое ускорение тела определим методом дифференцирования:
— угловая скорость, рад/с;
— угловое ускорение, рад/с².
Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .
Модуль линейной скорости:
.
Ускорение точки М при известной траектории определяется по его составляющим :
,
где .
В итоге, получаем формулы
тангенциальное ускорение: ;
нормальное ускорение: .

Плоско-параллельное движение твердого тела

Плоско-параллельное движение твердого тела — это движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости.
Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений:
1) поступательного и вращательного;
2) вращательного относительно подвижного (мгновенного) центра.
В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса.
В качестве полюса может быть принята любая точка сечения.
Уравнения движения запишутся в виде:
.
Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса.
Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P.
В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения:
.
Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.
.
Положение мгновенного центра вращения может быть определено на основании следующих свойств:
1) вектор скорости точки перпендикулярен радиусу;
2) модуль скорости точки пропорционален расстоянию от точки до центра вращения ();
3) скорость в центре вращения равна нулю.
Теорема:проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены.
Доказательство: расстояние АВ изменяться не может, следовательно, не может быть больше или меньше .
Вывод:.

Сложное движение точки

Относительное движение — это движение точки относительно подвижной системы.
Переносное движение — это движение точки вместе с подвижной системой.
Абсолютное движение — это движение точки относительно неподвижной системы.
Соответственно называют скорости и ускорения:
— относительные;
— переносные;
— абсолютные.
Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (согласно теореме о сложении скоростей):
.
Абсолютное значение скорости определяется по теореме косинусов:
.
Ускорение по правилу параллелограмма определяется только при поступательном переносном движении
.
.
При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым.
,
где .
Кориолисово ускорение численно равно:
,
где – угол между векторами и .
Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.

Динамика

Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.

Основные понятия динамики

Инерционность — это свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.

Масса — это количественная мера инерционности тела. Единица измерения массы — килограмм (кг).

Материальная точка — это тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.

Центр масс механической системы — геометрическая точка, координаты которой определяются формулами:

где m_k, x_k, y_k, z_k — масса и координаты k-той точки механической системы, m — масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.

Момент инерции материального тела относительно оси – это количественная мера инертности при вращательном движении.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:
.
Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:

Сила инерции материальной точки — это векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения:

Сила инерции материального тела — это векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс: ,
где — ускорение центра масс тела.

Элементарный импульс силы — это векторная величина , равная произведению вектора силы на бесконечно малый промежуток времени dt:
.
Полный импульс силы за Δt равен интегралу от элементарных импульсов:
.

Элементарная работа силы — это скалярная величина dA, равная скалярному произведению вектора силы на бесконечно малое перемещение .
Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:
,
где α — угол между направлениями векторов перемещения и силы.

Работа силы на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению:
.
Единица измерения работы — Джоуль (1 Дж = 1 Н·м).

Количество движения материальной точки — это векторная величина , равная произведению массы m на её скорость :
.

Количество движения механической системы равно векторной сумме количества движения её точек.
или
,
где m — масса механической системы, — вектор скорости центра масс системы.

Кинетическая энергия материальной точки — это скалярная величина Т, равная половине произведения массы точки на квадрат её скорости:
.

Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек:
.

Аксиомы динамики

Первая аксиома — это закон инерции.
Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения.
Вторая аксиома — закон пропорциональности ускорения.
Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы: — это основной закон динамики.
Третья аксиома — это закон противодействия.
Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны:
.
Четвертая аксиома — закон независимости действия сил.
При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы:

Дифференциальные уравнения динамики

Дифференциальные уравнения движения точки связывают ускорение точки с действующими на нее силами. Фактически дифференциальные уравнения являются записью основного закона динамики в явной дифференциальной форме.
Для абсолютного движения точки (движение в инерциальной системе отсчета) дифференциальное уравнение имеет вид:
.
Векторное уравнение может быть записано в проекциях на оси прямоугольной инерциальной системы координат:
При известной траектория движения точки уравнение может быть записано в проекциях на оси естественной системы координат:
С учетом того, что ,
где — тангенциальное ускорение;
— нормальное ускорение,
уравнения примут вид:

Общие теоремы динамики

Общие теоремы динамики устанавливают зависимость между мерами механического движения и механического взаимодействия. Выводы теорем являются результатом тождественного преобразования основного закона динамики.
Теорема об изменении количества движения: изменение количества движения материальной точки (механической системы) за конечный промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени — для материальной точки;
— для механической системы.
Теорема об изменении кинетической энергии: изменение кинетической энергии точки (механической системы) при её перемещении равно сумме работ всех действующих внешних сил на этом перемещении — для материальной точки;
— для механической системы.
Кинетическая энергия механической системы определяется в соответствии с , при этом для твердых тел выведены следующие зависимости:
— при поступательном движении тела;
— при вращательном движении тела;
— при плоско-параллельном движении тела.
Момент инерции цилиндра относительно его оси:
.
Момент инерции стержня относительно оси z:
.
Момент инерции прямоугольной пластины относительно осей х и y: .
Момент инерции шара определяется по формуле:
.
Работа силы тяжести:
,
где P — сила тяжести;
h — изменение положения тела по вертикали.
Работа силы при вращательном движении тела
,
где M — момент силы,
w — угловая скорость тела.
Следует иметь в виду, что работа, как скалярная величина, может быть положительной или отрицательной. Работа будет положительной если направление действия силы совпадает с направлением движения.

Принцип Даламбера

Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной:
.
Для механической системы:
.

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Дано: P = 10 Н; α = 45°
Найти: N, T — ?

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим:
.

Ответ: .

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
.

Опуская промежуточные выражения, получаем уравнение траектории:
.

Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).

Ответ: .

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Дано: m = 10 кг; a = 0,5 м/с 2 .
Найти: F — ?

Решение.
Согласно основному закону динамики: .

Подставив значения в формулу, получим:

Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с 2 , равна 5 Н.

В помощь студенту

Формулы, правила, законы, теоремы, уравнения, примеры решения задач

Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.

[spoiler title=”источники:”]

Момент силы и правило моментов

Теоретическая механика. В помощь студенту

[/spoiler]

Источник

Момент силы

«Кто овладел творениями Архимеда,

будет меньше удивляться открытиям

самых великих людей нашего времени»

Г.В. Лейбниц

В данной теме разговор пойдёт о моменте силы.

В прошлой теме говорилось о простых механизмах, которые служат для преобразования механического действия на тело, позволяя изменить точку приложения силы, ее модуль и направление. Выяснили, что рычагом является любое твердое тело, которое может поворачиваться относительно неподвижной опоры или оси.

Разделили рычаги на два вида — рычаг первого и рычаг второго рода. Рычагом первого рода называется рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону. Рычагом второго рода называется рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу. Расстояние от точки опоры до прямой, вдоль которой действует сила, называется плечом силы.

Вывели условие равновесия рычага, согласно которому, рычаг находится в равновесии при условии, что приложенные к нему силы обратно пропорциональны длинам их плеч.

Применим основное свойство пропорции для условия равновесия рычага. Тогда условие равновесия рычага примет вид:

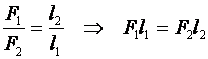
Произведение модуля силы на ее плечо — это новая физическая величина, которая называется моментом силы (обозначается буквой М).

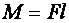
Измеряется момент силы в Ньютон-метрах (Н·м).

[M] = [Н·м]

Момент силы характеризует действие силы и показывает, что это действие зависит как от модуля силы, так и от ее плеча.

Сформулируем условие равновесия рычага через правило моментов: рычаг под действием двух создающих моменты сил находится в равновесии в том случае, если момент силы, вращающей рычаг по часовой стрелке, равен моменту силы, вращающей рычаг против часовой стрелки.

В рассмотренном в прошлой теме опыте силы, действующие на рычаг, были равны, соответственно, 8 Н и 4 Н, а их плечи составляли 2,5 и 5 делений рычага соответственно. Т.е. моменты этих сил равны при равновесии рычага.

А возможно ли равновесие рычага, когда на него действует более двух сил? Да, возможно. Рассмотрим рисунок.

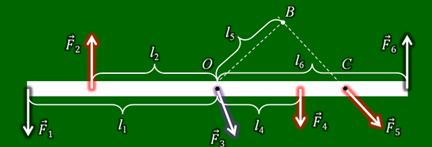
На нем изображен рычаг и несколько сил, действующих на него. Чтобы такой рычаг находился в равновесии нам необходимо:

1. Найти сумму моментов всех сил, вращающих рычаг по часовой стрелке.

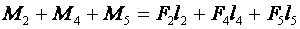
Необходимо отметить, плечо силы F₅ — это не расстояние OC, а расстояние OB — кратчайшее по перпендикуляру к прямой CB.

2. Найти сумму моментов сил, вращающих рычаг против часовой стрелки.

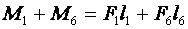
3. Сравнить сумму моментов всех сил, вращающих рычаг по часовой стрелки и сумму моментов сил, вращающих рычаг против часовой стрелки.

И если эти суммы равны между собой, то рычаг будет находиться в равновесии.

Возникает вопрос: Почему не учли силу F₃? Если посмотреть на рисунок, то можно заметить, что плечо этой силы равно нулю. Значит и момент ее равен нулю, и она не влияет на равновесие рычага.

Правило моментов (или условие равновесия рычага) лежит в основе действия различного вида инструментов и устройств, применяемых как в технике, так и в быту там, где требуется получить выигрыш в силе.

Давайте рассмотрим некоторые из них.

Ножницы — рычаг первого рода, ось вращения которого проходит через винт, соединяющий их две половинки. В зависимости от назначения, устройство ножниц бывает различным.

Например, для резки бумаги применяются ножницы, длина лезвий которых сопоставима с длиной ручек, так как при резке бумаги нет необходимости прикладывать большую силу. Ножницы, предназначенные для резки металла, имеют более длинные, по сравнению с размерами лезвия, ручки, так как сила сопротивления металла достаточно большая. И для того чтобы ее уравновесить, необходимо увеличивать плечо действующей силы. А в кусачках — инструменте, предназначенном для «перекусывания» проволоки — разница между длиной режущей части и ручками еще больше.

Рычаги можно обнаружить и в педалях автомобиля, и в клавишах пианино, рукоятки тисков и рычаге сверлильного станка. Также на принципе рычага основано действие рычажных весов. Например, учебные весы или весы, стоящие в магазинах, действуют как равноплечий рычаг.

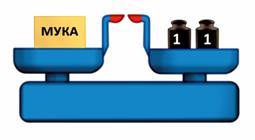
Множество рычагов можно найти в теле человека, животных, насекомых и птиц. Две кости, соединенные суставом и мышца, прикрепленная к этим костям, и представляют собой самый обычный рычаг.

Рычаги присутствуют даже в растениях. Для примера рассмотрим шалфей обыкновенный. Хоть он и называется «обыкновенным», но он не такой простой цветок.

По своей форме его цветки немного напоминают раскрытую пасть змеи. Из-под верхней «губы» даже высовывается «жало» — это две далеко вытянутые тычинки цветка. Внутри цветка на дне крохотной воронки светится капелька сладкого нектара. Этим нектаром шалфей приманивает шмеля, который и опыляет его. Как только насекомое залезает внутрь цветка за нектаром, из-под верхнего лепестка появляются две тычинки на длинных ножках и касаются спинки шмеля, обсыпая ее пыльцой. Потом шмель перелетает на другой цветок шалфея, залезает внутрь, и пыльца с его спинки попадает прямо на рыльце пестика, а цветку только это и нужно.

Где же у цветков шалфея рычаг? Оказывается, это тычинки с пыльцой. От оси у тычинок цветка отходят два плеча— длинное и короткое. На конце длинного, похожего на коромысло, плеча висит пыльцевой мешочек. А короткое плечо сплющено и закрывает вход в глубину цветка. Подтянется шмель своим хоботком к нектару и обязательно толкнет короткое плечо. А оно тотчас приведет в движение длинное плечо-коромысло. То в свою очередь ударяет по спине шмеля своими пыльниками — вот и сработал рычаг. А шмель летит дальше, касается рыльца пестика нового цветка и опыляет его.

Упражнения.

Задача 1. Определите, с какой силой натянута мышца бицепса при подъеме ядра массой 10 кг, если расстояние от центра ядра до локтя составляет 32 см, а от локтя до места крепления мышцы — 4 см?

Задача 2. На рисунке изображен рычаг, на котором имеются крючки, прикрепленные через одинаковые расстояния. Крючки пронумерованы от минус 3 до 3, причем ноль приходится на середину рычага. К некоторым крючкам прикреплено по нескольку грузов одинаковой массы. Имеется еще один такой же не подвешенный груз. К крючку с каким номером его нужно подвесить, чтобы рычаг находился в равновесии?

Основные выводы:

– Момент силы — это физическая величина, равная произведению модуля силы, вращающей тело, на ее плечо.

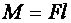
– Единицей измерения момента силы является Ньютон-метр.

[M] = [Н·м]

– Правило моментов: рычаг под действием двух создающих моменты сил находится в равновесии в том случае, если момент силы, вращающей рычаг по часовой стрелке, равен моменту силы, вращающей рычаг против часовой стрелки.

Стр. 175 — 176 читать

Источник

Определение

Статика — раздел механики, изучающий условия равновесия тел.

Виды равновесия

Устойчивое равновесие
	Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (E_{p min}).
Неустойчивое равновесие
	Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (E_{p max}).
Безразличное равновесие
	При выведении тела из положения безразличного равновесия дополнительных сил не возникает.

Момент силы

Определение

M = Fd

Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.

M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)

Момент силы может быть положительным и отрицательным.

Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:

M₁ = F₁d₁

Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:

M₂ = F₂d₂

Правило моментов

∑Mi=0

Иначе правило моментов можно сформулировать так:

∑Mпо час. стр.=∑Mпр. час. стр.

Условия равновесия тел

Тело не участвует в поступательном движении:	∑→Fi=0; →vo=0
Тело не участвует во вращательном движении:	∑Mi=0; ω0=0
Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении)	∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0

Простые механизмы

Определение

Наклонная плоскость
	Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg
Рычаг
	Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1
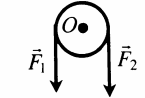
Неподвижный блок
	Изменяет направление действия силы. Модули и плечи сил при этом равны: F₁= F₂ M₁ = M₂
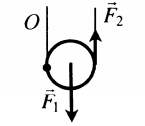
Подвижный блок
	Дает выигрыш в силе в 2 раза: d₁ = R d₂= 2R F₁= 2F₂
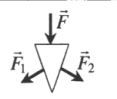
Клин
	Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2

Золотое правило механики

Задание EF22660

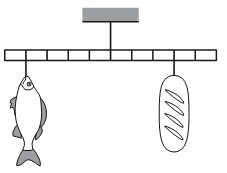Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.

Алгоритм решения

1.Записать исходные данные.

2.Записать правило моментов и выполнить решение в общем виде.

3.Подставить известные данные и вычислить искомую величину.

Решение

d₁ = 0,3

d₂ = 0,4

Запишем правило моментов:

F₁ d₁ = F₂ d₂

Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:

m₁gd₁ = m₂gd₂

m₁d₁ = m₂d₂

Отсюда масса рыбы равна:

m2=m1d1d2=0,8·0,30,4=0,6 (кг)

Ответ: 0,6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18706

Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения F_тр относительно оси, проходящей через точку О₃ перпендикулярно плоскости чертежа, равно…

Ответ:

а) 0

б) О₂О₃

в) О₂В

г) О₃В

Алгоритм решения

Сформулировать определение плеча силы.
Найти плечо силы трения и аргументировать ответ.

Решение

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 9.5k

Источник

Момент силы
$vec{M}=left[vec{r}timesvec{F}right]$
Размерность	L²MT⁻²
Единицы измерения
СИ	Н·м
СГС	Дина-сантиметр
Примечания
Псевдовектор

Моме́нт си́лы (момент силы относительно точки) — векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. Определяется как векторное произведение радиус-вектора точки приложения силы ${vec {r}}$ и вектора силы $vec{F}$ . Моменты сил, образующиеся в разных условиях, в технике могут иметь названия: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент, скру́чивающий момент.

Момент силы обозначается символом ${vec {M}}$ или, реже, ${displaystyle {vec {tau }}}$ (тау).

Единица измерения в СИ: Н⋅м. Величина момента силы зависит от выбора начала отсчёта радиус-векторов O.

Понятие момента силы используется, в основном, в области задач статики и задач, связанных с вращением деталей (рычагов и др.) в технической механике. Особенно важен случай вращения твёрдого тела вокруг фиксированной оси — тогда O выбирают на этой оси, а вместо самого момента рассматривают его проекцию на ось ${displaystyle M_{parallel }}$ ; такая проекция называется моментом силы относительно оси.

Наличие момента силы влечёт изменение момента импульса тела $vec{L}$ относительно того же начала O со временем $t$ : имеет место соотношение ${displaystyle d{vec {L}}/dt={vec {M}}}$ . В статике равенство нулю суммы моментов всех приложенных к телу сил является одним из условий (наряду с равенством нулю суммы сил) реализации состояния покоя.

Определение, общие сведения[править | править код]

В физике момент силы играет роль вращающего воздействия на тело.

Видеоурок: вращающий момент

В простейшем случае, если сила $vec{F}$ приложена к рычагу перпендикулярно ему и оси вращения, то момент силы определяется как произведение величины $F$ на расстояние $x$ от места приложения силы до оси вращения рычага, называемое «плечом силы»:

${displaystyle M=Fx}$ .

Например, сила в 3 ньютона, приложенная на расстоянии 2 м от оси, создаёт такой же момент, что и сила в 1 ньютон с плечом 6 м.

Если действуют две силы, говорят о моменте пары сил (такая формулировка восходит к трудам Архимеда). При этом равновесие достигается в ситуации ${displaystyle F_{1}x_{1}=F_{2}x_{2}}$ .

Для случаев более сложных движений и более сложных объектов определение момента как произведения ${displaystyle Fx}$ требует универсализации.

Момент силы иногда называют вращающим или крутящим моментом. «Вращающий» момент понимается в технике как внешнее усилие, прикладываемое к объекту, а «крутящий» — как внутреннее, возникающее в самом объекте под действием приложенных нагрузок (этим понятием оперируют в сопромате).

Момент силы относительно точки[править | править код]

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

В общем случае момент силы $vec{F}$ , приложенной к телу, определяется как векторное произведение

${displaystyle {vec {M}}=left[{vec {r}}times {vec {F}}right]}$ ,

где ${vec {r}}$ — радиус-вектор точки приложения силы. Вектор ${vec {M}}$ перпендикулярен векторам ${vec {r}}$ и $vec{F}$ .

Начало отсчета радиус-векторов O может быть любым. Обычно O выбирают в чем-либо выделенной точке: в месте закрепления подвеса, в центре масс, на оси вращения и т.д.. Если одновременно анализируется момент импульса тела $vec{L}$ , то начало O всегда выбирается одинаковым для $vec{L}$ и ${vec {M}}$ .

Если не оговорено иное, то «момент силы» — это момент силы относительно точки (O), а не некоей оси.

В случае нескольких приложенных сосредоточенных сил их моменты векторно суммируются:

${displaystyle {vec {M}}=sum _{i}left[{vec {r}}_{i}times {vec {F}}_{i}right]}$ ,

где ${displaystyle {vec {r}}_{i}}$ — радиус-вектор точки приложения $i$ -й силы ${displaystyle {vec {F}}_{i}}$ . В случае силы, распределённой с плотностью ${displaystyle d{vec {F}}/dV}$ ,

${displaystyle {vec {M}}=int limits _{V}left[{vec {r}}times {frac {d{vec {F}}}{dV}}right]dV}$ .

Если ${displaystyle d{vec {F}}/dV}$ (Н/м³) — обобщённая функция, которая может содержать и дельтаобразные члены, то последней формулой охватываются и две предыдущие.

Момент силы относительно оси[править | править код]

Моментом силы относительно оси называется алгебраическое значение проекции момента ${vec {M}}$ на ось, то есть

${displaystyle M_{parallel }={vec {M}}cdot {vec {e}}_{o}}$ ,

где ${displaystyle {vec {e}}_{o}}$ — единичный вектор вдоль оси, а начало отсчёта O выбрано на оси. Момент силы относительно оси может быть рассчитан как

${displaystyle M_{parallel }=pm left|{vec {r}}_{perp }times {vec {F}}_{perp }right|}$ ,

где через ${displaystyle {vec {r}}_{perp }}$ и ${displaystyle {vec {F}}_{perp }}$ обозначены составляющие радиус-вектора и силы в плоскости, перпендикулярной оси.

В отличие от момента силы ${vec {M}}$ , величина момента силы относительно оси ${displaystyle M_{parallel }}$ не претерпевает изменения при сдвиге точки O вдоль оси.

Для краткости символ параллельности и знак могут опускаться, а ${displaystyle M_{parallel }}$ (как и ${vec {M}}$ ) именоваться «моментом силы».

Единицы измерения[править | править код]

Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.

Формально, размерность ${vec {M}}$ (Н·м) совпадает с размерностями энергии и механической работы.

Некоторые примеры[править | править код]

Формула момента рычага[править | править код]

Момент, действующий на рычаг

Момент силы, действующей на рычаг, равен

${displaystyle {vec {M}}=rFsin alpha cdot {vec {e}}_{o}}$

или, если записать момент силы относительно оси,

${displaystyle M_{parallel }=rFsin alpha }$ ,

где $alpha$ — угол между направлением силы и рычагом. Плечо силы равно ${displaystyle rsin alpha }$ . Максимальное значение момента достигается при перпендикулярности рычага и силы, то есть при ${displaystyle alpha =pi /2}$ . При сонаправленности $vec{F}$ и рычага момент равен нулю.

Статическое равновесие[править | править код]

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма моментов всех сил вокруг любой точки.

Для двумерного случая с горизонтальными и вертикальными силами требование сводится к тому, чтобы нулевыми были сумма сил в двух измерениях: ${displaystyle Sigma F_{horizontal}=0,,Sigma F_{vertical}=0}$ и момент силы в третьем измерении: ${displaystyle Sigma M=0}$ .

Движение твёрдого тела[править | править код]

Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.

Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.

${displaystyle {vec {L_{o}}}=I_{c},{vec {omega }}+[M({vec {r_{o}}}-{vec {r_{c}}}),{vec {v_{c}}}].}$

Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.

Продифференцируем это выражение по времени. И если $I$ — постоянная величина во времени, то

${displaystyle {vec {M}}=I{frac {d{vec {omega }}}{dt}}=I{vec {alpha }},}$

где ${displaystyle {vec {alpha }}}$ — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с²). Пример: вращается однородный диск.

Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:

${displaystyle {vec {M_{c}}}=I_{c}{frac {d{vec {omega }}}{dt}}+[{vec {w}},I_{c}{vec {w}}].}$

Связь с другими величинами[править | править код]

С моментом импульса[править | править код]

Момент силы — производная момента импульса ${displaystyle {vec {L}}={vec {r}}times {vec {p}}}$ относительно точки O по времени:

${displaystyle {vec {M}}={frac {d{vec {L}}}{dt}}}$ ,

Аналогичную формулу можно записать для моментов относительно оси:

${displaystyle M_{parallel }={frac {dL_{parallel }}{dt}}}$ .

Если момент силы ${vec {M}}$ или ${displaystyle M_{parallel }}$ равен нулю, момент импульса относительно соответствующей точки или оси сохраняется.

С мощностью[править | править код]

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу и развивает мощность ${displaystyle {vec {F}}cdot {vec {v}}}$ (где $vec{v}$ — скорость материальной точки). Так же и в случае момента силы: если он совершает действие через «угловое расстояние», развивается мощность

${displaystyle P={vec {M}}cdot {vec {omega }}}$ .

В системе СИ мощность $P$ измеряется в ваттах, угловая скорость $vec{omega}$ — в радианах в секунду.

С механической работой[править | править код]

Если под действием момента силы ${vec {M}}$ происходит поворот тела на угол $dvarphi$ , то совершается механическая работа

${displaystyle dA=left|{vec {M}}right|dvarphi }$ .

Для поворота, скажем, рычага вокруг фиксированной оси на угол ${displaystyle varphi _{2}-varphi _{1}}$ получим

${displaystyle A=int _{varphi _{1}}^{varphi _{2}}left|{vec {M}}right|dvarphi =left|{vec {M}}right|(varphi _{2}-varphi _{1})=left|{vec {M}}right|int _{t_{1}}^{t_{2}}omega (t)dt}$ .

В системе СИ работа $A$ измеряется в джоулях, угол — в радианах.

Размерность работы (и энергии) совпадает с размерностью момента силы («ньютон-метр» и джоуль — это одни и те же единицы). Момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию $2pi$ джоуля.

Измерение момента силы[править | править код]

Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.

Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.

Из истории понятия[править | править код]

Для того чтобы понять, откуда появилось понятие момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы ${vec {F}}$ на рычаг ${vec {r}}$ , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием силы конец рычага смещается на бесконечно малый отрезок $dl$ , которому соответствует бесконечно малый угол $dvarphi$ . Обозначим через ${displaystyle d{vec {l}}}$ вектор, который направлен вдоль бесконечно малого отрезка $dl$ и равен ему по модулю. Угол между векторами ${vec {F}}$ и ${displaystyle d{vec {l}}}$ равен $beta$ , а угол между векторами ${vec {r}}$ и ${vec {F}}$ равен $alpha$ .

Следовательно, бесконечно малая работа $dA$ , совершаемая силой ${vec {F}}$ на бесконечно малом участке $dl$ , равна скалярному произведению вектора ${displaystyle d{vec {l}}}$ и вектора силы, то есть ${displaystyle dA={vec {F}}cdot d{vec {l}}}$ .

Теперь попытаемся выразить модуль вектора ${displaystyle d{vec {l}}}$ через радиус-вектор ${vec {r}}$ , а проекцию вектора силы ${vec {F}}$ на вектор ${displaystyle d{vec {l}}}$ — через угол $alpha$ .

Так как для бесконечно малого перемещения рычага $dl$ можно считать, что траектория перемещения перпендикулярна рычагу ${vec {r}}$ , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: ${displaystyle dl=rmathrm {tg} ,dvarphi }$ , где в случае малого угла справедливо ${displaystyle mathrm {tg} ,dvarphi =dvarphi }$ и, следовательно, ${displaystyle left|d{vec {l}}right|=left|{vec {r}}right|dvarphi }$ .

Для проекции вектора силы ${vec {F}}$ на вектор ${displaystyle d{vec {l}}}$ видно, что угол ${displaystyle beta ={frac {pi }{2}}-alpha }$ , а так как ${displaystyle cos {left({frac {pi }{2}}-alpha right)}=sin alpha }$ , получаем, что ${displaystyle left|{vec {F}}right|cos beta =left|{vec {F}}right|sin alpha }$ .

Теперь запишем бесконечно малую работу через новые равенства: ${displaystyle dA=left|{vec {r}}right|dvarphi left|{vec {F}}right|sin alpha }$ , или ${displaystyle dA=left|{vec {r}}right|left|{vec {F}}right|sin alpha ,dvarphi }$ .

Видно, что произведение ${displaystyle left|{vec {r}}right|left|{vec {F}}right|sin alpha }$ есть не что иное, как модуль векторного произведения векторов ${vec {r}}$ и ${vec {F}}$ , то есть ${displaystyle left|{vec {r}}times {vec {F}}right|}$ , которое и было принято обозначить за момент силы $M$ , или модуль вектора момента силы ${displaystyle left|{vec {M}}right|}$ .

Теперь полная работа записывается просто: ${displaystyle A=int limits _{0}^{varphi }left|{vec {r}}times {vec {F}}right|dvarphi }$ , или ${displaystyle A=int limits _{0}^{varphi }left|{vec {M}}right|dvarphi }$ .

См. также[править | править код]

Момент инерции
Момент импульса
Теорема Вариньона

Источник

Примеры составления суммы моментов сил

Расчет суммы моментов относительно точки, к которой приложена сила

Определение суммы моментов относительно точки, в которой приложен момент

Сумма моментов относительно точки, где действует распределенная нагрузка

iSopromat.ru

Правило знаков проекций сил

Правило знаков для моментов

Момент силы и правило моментов

теория по физике 🧲 статика

Виды равновесия

Устойчивое равновесие

Неустойчивое равновесие

Безразличное равновесие

Момент силы

Правило моментов

Условия равновесия тел

Простые механизмы

Наклонная плоскость

Рычаг

Неподвижный блок

Подвижный блок

Теоретическая механика. В помощь студенту

Статика твердого тела

Кинематика

Динамика

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

В помощь студенту

Виды равновесия

Устойчивое равновесие

Неустойчивое равновесие

Безразличное равновесие

Момент силы

Правило моментов

Условия равновесия тел

Простые механизмы

Наклонная плоскость

Рычаг

Неподвижный блок

Подвижный блок

Клин

Определение, общие сведения[править | править код]

Момент силы относительно точки[править | править код]

Момент силы относительно оси[править | править код]

Единицы измерения[править | править код]

Некоторые примеры[править | править код]

Формула момента рычага[править | править код]

Статическое равновесие[править | править код]

Движение твёрдого тела[править | править код]

Связь с другими величинами[править | править код]

С моментом импульса[править | править код]

С мощностью[править | править код]

С механической работой[править | править код]

Измерение момента силы[править | править код]

Из истории понятия[править | править код]

См. также[править | править код]

Вам также может понравиться

Как найти заметки в контакт

Как найти человека по геолокации телефона онлайн

Экран телефона не показывает кто звонит как исправить

Добавить комментарий Отменить ответ