- Учебники
- 5 класс
- Математика 👍
- Мерзляк
- №187

Найдите сумму наиболее удобным способом:
1) 1 + 2 + 3 + …+ 9 + 10;
2) 1 + 2 + 3 + … + 99 + 100.

reshalka.com
Математика 5 класс Мерзляк. Номер №187
Решение 1
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5 + 10 = 10 + 10 + 10 + 10 + 5 + 10 = 55
Решение 2
1 + 2 + 3 + … + 99 + 100 = (1 + 100) + (2 + 99) + (3 + 98) + … + (50 + 51) = 101 * 50 = 5050, так как число слагаемых сто, то пар слагаемых − 50
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Как найти сумму наиболее удобным способом?
Займы
Анонимный вопрос
19 декабря 2017 · 562
ОтветитьУточнить
Эльса М.8,5 K
Всем трям, то есть здравствуйте. 🙂 Я по жизни оптимист, натуралист, огородник-грядковод… · 18 февр 2019
Как известно, от перемены мест слагаемых сумма не меняется, поэтому при вычислении суммы из многих слагаемых можно их сгруппировать так, чтобы удобнее было вычислять. Например: 25+7+5+13+21+9=(25+5)+(7+13)+(21+9)=30+20+30=80
463
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
скрыт(Почему?)
ГДЗ и решебники
вип уровня
- ГДЗ
- 5 класс
- Математика
- Мерзляк
- Упражнение 187

Условие
Найдите сумму наиболее удобным способом:
1) 1 + 2 + 3 +…+ 9 + 10;
2) 1 + 2 + 3 +… + 99 + 100.
Решение 1

Решение 2

Решение 3
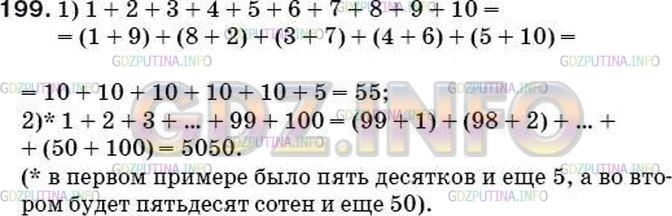
Решение 4
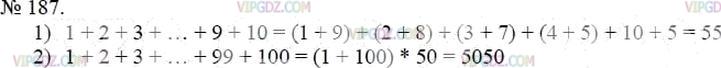
Популярные решебники
Лучший ответ
Леонид Фурсов
Высший разум
(787484)
13 лет назад
Считать как сумму арифметической прогрессии: a1=1; d=1; S=((2*a1+d*(100-1))*100)/2=((2+100-1)*50)=101*50;
Источник: прогрессия
Остальные ответы
Ксюшка
Профи
(573)
13 лет назад
нужно складывать числа 1+99+2+98+3+97 и т д и получится сумма
Eldar Nezametdinov
Мыслитель
(5054)
13 лет назад
The answer is 5050 because you group like this:
100 + 1 = 101
99 + 2 = 101
98 + 3 = 101
….
51 + 50 = 101
That’s fifty pairs that add to 101:
101 × 50 = 5050
ПОЧТА ПОЧТА
Профи
(569)
13 лет назад
1 + 100 = 2 + 99 и т. д. сумма 101, таких сумм 100/2 = 50. итого 101 х 50 = 5050
Берёзка белая
Мыслитель
(8419)
13 лет назад
великий Гаусс
1+2+3+…+99+100= (1+100)+(2+99)+…+(50+51)=101*50=5050
Юлия Марунова
Мастер
(1203)
13 лет назад
Ой, так это легко=)
Если расписать всю сумму, то получится, что если брать пары чисел (одно в начале, другое с конца) , то каждая такая пара будет равна
1+100=101
2+99=101
3+98=10 и т. д.
таких пар будет 100/2=50
и сумма равна 101*55=5050
777
Ученик
(222)
6 лет назад
Можете помочь 1+3+5+…+27+29
25.09.2011 15:37
Помогите решить! Найдите наиболее удобным способом сумму всех трехзначных чисел. Спасибо!
25.09.2011 15:41
999+101, 998+102 и т.д. Прикиньте сами, сколько будет таких пар и умножьте это число на 1100.
![]()
Anonymous
25.09.2011 15:44
Первое – 100, второе – 101, третье -102,…предпоследнее – 998,последнее – 999. Если сложить второе и последнее получим 1100, третье и предпоследнее получим 1100. Таких пар будет 449. 1100*449+100=494000.
25.09.2011 15:46
Ответ 494550
![]()
Anonymous
25.09.2011 15:50
Точно, еще 550 забыла, которое без пары осталось.
25.09.2011 15:52
А сотня тоже ведь без пары
![]()
Anonymous
25.09.2011 15:53
Так сотню я учла: 1100*449+100=494000, а 550 забыла.
25.09.2011 15:46
Подсказываю, выписываем ряд трехзначных чисел в прямом и в обратном порядке 100 101 102 …..998 999 далее в обратном 999 998 997 …..101 100 Обращаем внимание, что сумма каждой пары чисел 1099 всего таких пар 900. Итак два раза просуммированный ряд = 1099х900. Половина этого произведения и будет искомой суммой всех трехзначных чисел. 🙂 Вообще это частный случай арифметической прогрессии.
25.09.2011 15:54
:party1
25.09.2011 15:52
Удобнее всего считать методом Гаусса, который учитывает закономерность, присущую арифметической прогрессии. 100, 101, 102,…., 999 (100+999)+(101+998)+….. 1099 Х 900/2 = 494 550
25.09.2011 19:05
А помнишь, а выкладывала задачку, которую Эшли придумала на Ряды Гаусса, когда ей лет 7-8 было? Я ее тогда с ее слов записала и сохранила. Вот она: В волшебной стране Математика, в маленьком городке Ряды Гаусса жили-были в одном классе дети, у которых вместо имен были …номера! И было в этом классе 23 ученика.У них и футболки были с номерами: 1-й,2-й,3-й,….22-й,23-й. Вот как-то учительница и говорит: “Сегодня мы идём в Парк аттракционов! Но сначала скажите мне, кто сегодня отсутствует”. Выяснилось, что 1-го и 2-го нет. Ладно, значит в классе сейчас 21 ученик. Пришли они в Парк. А контролер говорит,что вместо входных билетиков сегодня надо решить маленькую задачку, причем устно! Надо сказать сумму всех чисел, которые написаны на футболках. Опечалились ребята, трудно ведь сложить все числа,да еще и устно… Но учительница попросила всех встать в РЯД по порядку: 3,4,5,…22,23. Потом хотела построить всех парами, но ведь 21-го человека парами не поставишь… Пришлось ей ученика номер 3 попросить отойти в сторонку. Стоит 3-й там и грустно наблюдает за остальными ребятами. А учительница оставшихся 20 человек построила парами, да причем так хитро. 4-го и 23-го, 5-го и 22-го, 6-го и 21-го.То есть последнего из ряда и первого. Пар получилось 10 (20:2) и в каждой паре сумма была 27 (23+4, 22+5…) ” У нас получилось 270! ” – закричали радостно ребята. И тут все заметили грустного 3-го, который уже собирался плакать. “Нет, ребята. Наша сумма 273!” – сказала учительница и обняла 3-го. (270+3) Конечно весь класс пригласили пройти в Парк. И ребята катались на всех горках и каруселях целый день!:)
26.09.2011 03:13
Не, не помню такую историю. Очень забавно 🙂
25.09.2011 15:38
А чьи дети сами учатся? Без мам, без Евы?
![]()
Anonymous
25.09.2011 15:58
Мой сам учится.
25.09.2011 16:00
А меня ребенок многому научил 🙂
25.09.2011 16:00
и мой 🙂 но они русский-математику в продлёнке делают
25.09.2011 16:02
Лучше с мамами. Так мамы хоть что-то узнают. 🙂 🙂 🙂
25.09.2011 16:06
Спасибо Вам, Умницы!
![]()
Anonymous
25.09.2011 19:48
Те, у кого учителя объясняют лучше пап и мам
![]()
Anonymous
25.09.2011 20:15
(с хордастью тянет руку) моя! моя! Родители у школы спрашивают учили ли мы стих и как решили ту или иную задачу, а я и знать не знаю. Сама все делает и пятерки в дневнике домой тащщит.
![]()
Anonymous
25.09.2011 19:14
О Карле Гауссе: Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 50 х 101 = 5050. В википедии о нем можно почитать.
25.09.2011 23:51
А я читала в учебнике сына для 12 класса ( англ школа – кембридж систем) что Гаусс сам, будучи учеником решил эту задачу таким образом, чем очень удивил учителя.
![]()
Anonymous
26.09.2011 03:16
Так выше так и написали 🙂

