Как найти сумму накопленного долга

Это слайд-шоу требует JavaScript.

Сущность простых процентов состоит в том, что процент по кредиту все время начисляется на первоначальную сумму кредита в течение всего срока действия кредита.

Например, если банк выдал клиенту в кредит 100 000 рублей на 2 года по ставке 10% годовых, то процент по кредиту и в первый и во второй год, при расчёте по формуле простого процента, составит 10 000 рублей (10 000*0,1).

К наращению простыми процентами прибегают при выдаче кредита сроком до 1 года или когда проценты  не присоединяются к основной сумме долга, а периодически выплачиваются.

Для записи формулы простых процентов примем следующие обозначения:

I — сумма денежных средств, начисленных на первоначальную сумму по процентам за весь период (сумма с процентами — первоначальная сумма)

P —  первоначальная сумма долга

S — сумма в конце срока (первоначальная сумма + сумма денежных средств по процентам)

i — процентная ставка, десятичная дробь. Например, если процентная ставка 20%, то в расчетах необходимо использовать 0,2 =20%/100

n — срок кредита в годах

Формула начисленных за весь срок процентов

I=Pni (I)

Формула простых процентов 

S=P+I=P+Pni=P(1+ni)   (II)

Вычисление первоначальной суммы долга по формуле простого процента

P=S/(1+ni) или P=S/(1+ni/100), если i измеряется в %  (III)

Вычисление годовой процентной ставки по формуле простого процента

i=(S/P-1)/n или i=(S/P-1)/n*100, если необходимо получить процентную ставку (IV)

Вычисление срока кредита по формуле простого процента

n=(S/P-1)/i  (V)

ПРАКТИКУМ

1.  ВЫЧИСЛЕНИЕ СУММЫ НАКОПЛЕННОГО ДОЛГА ПО ФОРМУЛЕ ПРОСТЫХ ПРОЦЕНТОВ

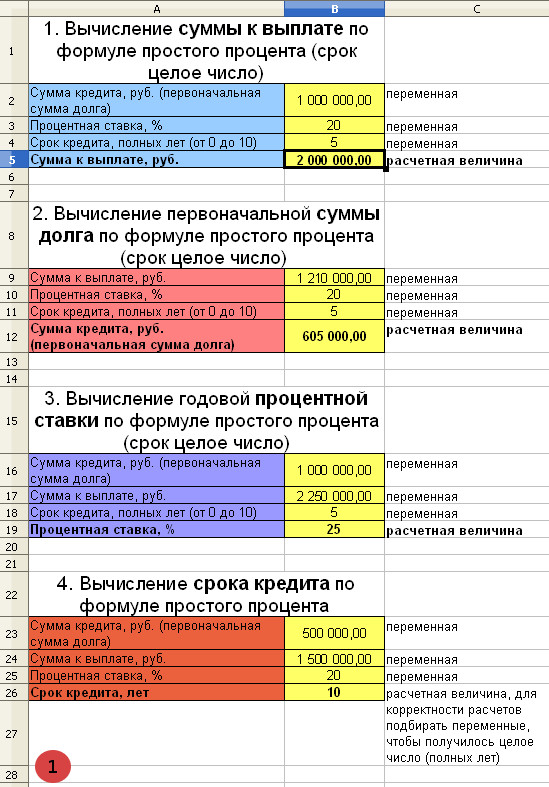
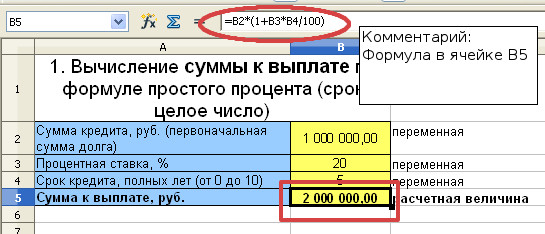
Банком выдан кредит в размере 1 000 000 рублей на 5 лет под 20% годовых. Необходимо определить сумму к погашению по кредиту по формуле простых процентов.

Первоначальная сумма кредита равна 1 000 000 рублей, P=1 000 000

Процентная ставка 20%, т.е. i=0,2

Срок кредита 5 лет, n=5

Сумма начисленных процентов за 5 лет по формуле простых процентов

I=Pni=1 000 000 * 5 *0,2=1 000 000

Сумма к выплате по кредиту

S=P+I=1 000 000 + 1 000 000=2 000 000 рублей

или

S=1 000 000(1+5*0,2)=2 000 000 рублей

1. ВЫЧИСЛЕНИЕ ПЕРВОНАЧАЛЬНОЙ СУММЫ ДОЛГА ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА

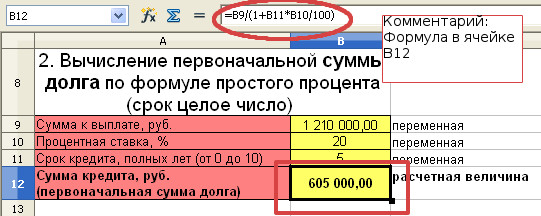
Клиент выплатил банку 1 210 000 рублей за кредит, который он взял на 5 лет назад под 20% годовых.  Кредит рассчитывался по формуле простых процентов. Определить первоначальную сумму долга.

Сумма, выплаченная банку равна 1210 000 рублей, S=1 210 000

Процентная ставка 20%, т.е. i=0,2

Срок кредита 5 лет, n=5

Для расчёта первоначальной суммы кредита воспользуемся формулой (III)

P=S/(1+ni)=1 210 000/(1+5*0,2)=605 000 рублей

Пять лет назад банк выдал клиенту кредит в размере 605 000 рублей.

1. ВЫЧИСЛЕНИЕ ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА

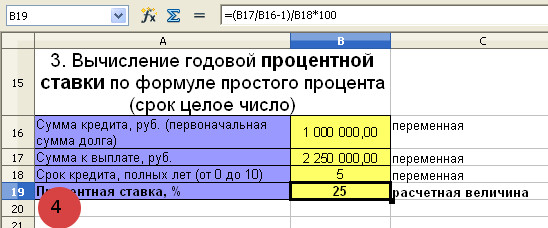
Банк выдал клиенту кредит в размере 1 000 000 рублей на 5 лет. Клиент вернул в банк 2 250 000 рублей. Определить годовую процентную ставку. В течение 5 лет процент начислялся на 1 000 000 рублей.

Первоначальная сумма кредита равна 1 000 000 рублей, P=1 000 000

Сумма, выплаченная банку равна 2 250 000 рублей, S=2 250 000

Срок кредита 5 лет, n=5

Для расчёта годовой процентной ставки по кредиту воспользуемся формулой (IV)

i=(S/P-1)/n=(2 250 000/1 000 000 – 1)/5=0,25 или 25%

Банк выдал кредит клиенту по ставке 25% годовых.

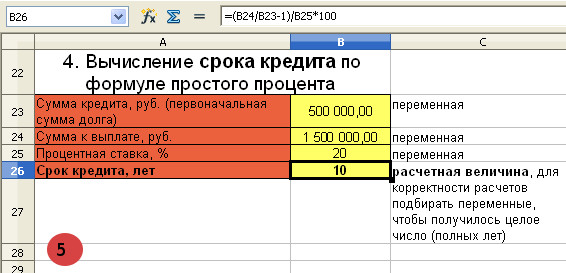
1. ВЫЧИСЛЕНИЕ СРОКА КРЕДИТА ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА

Банк выдал клиенту кредит в размере 500 000 рублей под 20% годовых. Клиент обязался вернуть кредит, когда сумма с процентами достигнет 1 500 000 рублей. Через сколько лет клиенту нужно отдать кредит, рассчитанный по формуле простого процента?

Первоначальная сумма кредита равна 500 000 рублей, P=500 000

Сумма, выплаченная банку равна 1 500 000 рублей, S=1 500 000

Процентная ставка 20%, т.е. i=0,2

Для вычисления срока кредита воспользуемся формулой (V)

n=(S/P-1)/i=(1 500 000/500 000-1)/0,2=10 лет

Клиент должен заплатить банку  1 500 000 рублей через 10 лет.

Сделаем вычисления в OpenOffice Calc по формуле простого процента.

OpenOffice Calc

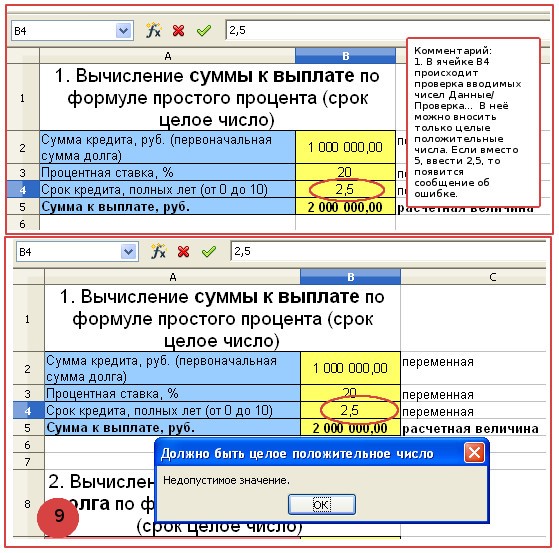
1. Исходная таблица с расчетами простого процента

 

1. Дополнительные настройки

1. Для корректности расчетов установим некоторые ограничения на вводимые в ячейку значения.

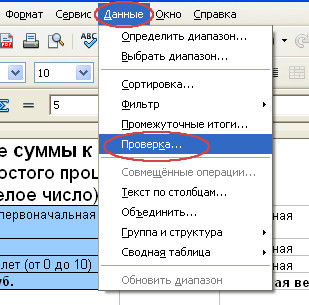
Например, сделаем так, чтобы в ячейку B4  можно было вводить только целые положительные числа.  Для этого выделим ячейку B4 и вызовем диалоговое окно “Проверка вводимых значений”, последовательно выбрав  Данные/Проверка…

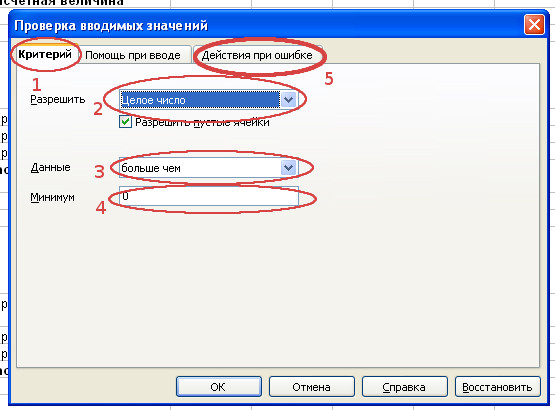
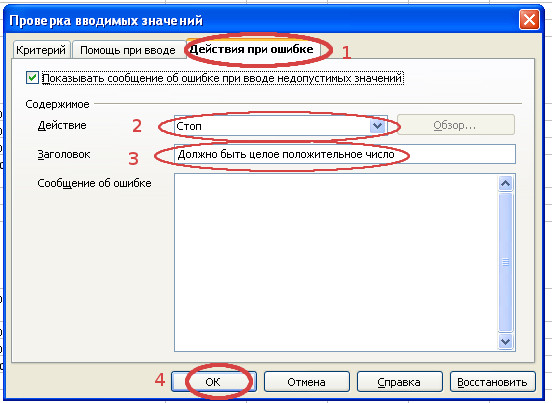
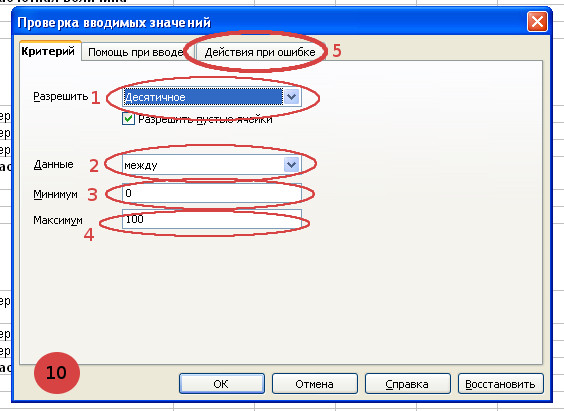
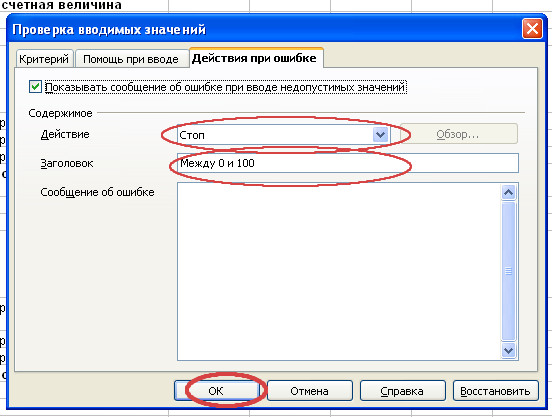
1. Последовательно заполним все пункты  диалогового окна “Проверка вводимых значений” в соответствии с примером.

1. Проверим, как работают данные ограничения. Теперь при вводе в ячейку B4 неправильных значений, например, 2,5 вместо 5, появляется сообщение об ошибке и возвращается исходное значение 5.

1. Установим ограничения на вводимые значения для ячейки B3. Теперь в ячейку должны вводиться десятичные положительные значения в диапазоне от 0 до 100.

Тема: Решение задач по финансам и кредиту

Раздел: Бесплатные рефераты по финансам и кредиту

Тип: Задача | Размер: 13.48K | Скачано: 246 | Добавлен 26.10.14 в 01:33 | Рейтинг: +1 | Еще Задачи

Вариант №3

Задача 1. Найти сумму накопленного долга и проценты, если ссуда 180000 руб. выдана на три года под простые 18% годовых. Во сколько раз увеличится наращенная сумма при увеличении ставки на 2%?

S₁ – сумма накопленного долга

S₂ – сумма накопленного долга при увеличении ставки на 2%

S₁ = 180 000 (1 + 0,18 * 3) = 180 000 * 1,54 = 277 200

S₂ = 180 000 (1 + (0,18 + 0,02) * 3) = 180 000 * 1,6 = 288 000

S₂ / S₁ = 180 000 * 1,6 / 180 000 * 1,54 = 1,6 / 1,54 = 1,03896 раза

Ответ:

Сумма накопленного долга 277 200, увеличится 1,03896 раза

Наращенная сумма при увеличении ставки на 2% увеличится в 1,03896 раза

Задача 2. Найти простую процентную ставку, эквивалентную сложной ставке 11%.

(1 + i_пр * n) = (1 + 0,11)ⁿ

i_пр = ((1 + 0,11)ⁿ – 1) / n

Задача 3. Какую сумму нужно положить в банк под 12% годовых мужчине 37 лет, чтобы по достижении им пенсионного возраста 60 лет в течение 15 лет в начале каждого месяца снимать по 10000 рублей, если проценты капитализируются:  в конце года; в конце каждого полугодия; в конце каждого квартала; в конце каждого месяца?

R – сумму, нужную положить в банк

S – наращенная сумма по достижении им пенсионного возраста 60 лет.

А = S

Капитализация в конце года:

А = 10 000 * (1 – (1 + 0,12) ^{– 15} )* (1 + 0,12) ^1/12 / ((1 + 0,12)^1/12 – 1) = 10 000 * 86,950887 = 869 508,87

S = R*(1 + 0,12)^{60 – 37} = R*(1 + 0,12) ²³

R = S / (1 + 0,12) ²³ = S / 13,552347 = 869 508,87 / 13,552347 = 64 159, 28

Капитализация в конце полугодия:

А = 10 000 * (1 – (1 + 0,12 / 2) ^{– 15 * 2} )* (1 + 0,12 / 2) ^2/12 / ((1 + 0,12 / 2)^2/12 – 1) = 10 000 * 85,456209 = 854 562,09

S = R*(1 + 0,12 / 2)^{(60 – 37)*2} = R*(1 + 0,06) ⁴⁶

R = S / (1 + 0,06) ⁴⁶ = S / 14,59049 = 854 562,09/ 14,59049 = 58 569, 81

Капитализация в конце квартала:

А = 10 000 * (1 – (1 + 0,12 / 4) ^{– 15 * 4} )* (1 + 0,12 / 4) ^4/12 / ((1 + 0,12 / 4)^4/12 – 1) = 10 000 * 84,681771= 846 817,71

S = R*(1 + 0,12 / 4)^{(60 – 37)*4} = R*(1 + 0,03) ⁹²

R = S / (1 + 0,03) ⁹² = S / 15,17137 = 846 817,71/ 15,17137 = 55 816, 84

Капитализация в конце месяца:

А = 10 000 * (1 – (1 + 0,12 / 12) ^{– 15 * 12} )* (1 + 0,12 / 12) ^12/12 / ((1 + 0,12 / 12)^12/12 – 1) = 10 000 * 84, 154881= 841 548,81

S = R*(1 + 0,12 / 12)^{(60 – 37)*12} = R*(1 + 0,01) ²⁷⁶

R = S / (1 + 0,01) ²⁷⁶ = S / 15,58473 = 841 548,81/ 15,58473 = 53 998, 31

Задача 4. Найти доходность к погашению облигации со сроком обращения 8 лет, номинальной стоимостью 3000 и купонной ставкой 8%, если: 1) она продаётся за 300, 2) её розничная цена увеличится на 10%, 3) уменьшится на 5%?

Купонный доход = 3 000 * 0,08 = 240

Сумма купонного дохода без капитализации процентов 240 * 8 = 1 920

i = ((1 920 + 3 000) / 300) ^0.125 – 1 = 0,4186 или 41,86%

Розничная цена увеличится на 10%

i = ((1 920 + 3 000) / 300 * 1,1) ^0.125 – 1 = 0,4018 или 40,18%

Розничная цена уменьшится на 5%

i = ((1 920 + 3 000) / 300 * 0,95) ^0.125 – 1 = 0,4277 или 42,77%

+1

26.10.14 в 01:33
Автор:dibily

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Решение экзаменационных задач по статистике
• Решение задач по инвестициям (задачи на дисконтирование)
• Примерные задачи для экзамена по Финансам организаций
• Типовые задачи по Страхованию
• Макроэкономика задачи с решением
• Задачи по Страхованию с решением
• На карточках написаны буквы К, О, Р, О, Б, О, К
• Профессиональная культура как подсистема государственного управления: сущность понятия, цели и задачи

Калькулятор неустойки по договору

Калькулятор расчета задолженности по договору — это инструмент для вычисления суммы долга и неустойки по данным, указанным в документах о заключении сделки. При необходимости пеня считается по закону.

Задолженность по договорным обязательствам

Статья 395 Гражданского кодекса РФ определяет порядок расчета процентов по долгу (или, как это написано в законе, за пользование чужими денежными средствами). Если человек или организация задолжали какую-то сумму, эти деньги используются, а значит, приносят доход. Но не их законному владельцу, а должнику. Чтобы определить точный размер неустойки, требуется калькулятор расчета процентов по задолженности и суммы долга. Использование сервиса совершенно бесплатно и требует минимум информации, но позволяет точно подсчитать, сколько денег требовать с должника на определенную дату.

Два способа для вычисления неустойки

Итак, разберемся, как происходит расчет неустойки по долгу. Онлайн-калькулятор процентов от суммы долга позволяет вычислить их размер по состоянию на заданную дату с учетом региона РФ. Почему важен регион? Это связано с тем, что в 2015 году Федеральным законом от 08.03.2015 № 42-ФЗ были внесены поправки в Гражданский кодекс РФ, в соответствии с которыми для расчета процентов за пользование чужими средствами больше не используется ставка рефинансирования ЦБ РФ. Теперь это средние ставки банковского процента по вкладам физических лиц, которые публикует Центробанк России по действующим в РФ федеральным округам:

• Центральный ФО;
• Северо-Западный ФО;
• Южный ФО;
• Северо-Кавказский ФО;
• Приволжский ФО;
• Уральский ФО;
• Сибирский ФО;
• Дальневосточный ФО.

Наш калькулятор расчета пени по кредиту разработан с учетом этих изменений в ГК РФ. Он поможет рассчитать суммы задолженности как по новой, так и по старой схеме, достаточно только указать, каким способом вам необходимо воспользоваться.

Как работать с калькулятором

Чтобы узнать, как посчитать проценты по просроченной задолженности с помощью калькулятора, достаточно трех параметров:

• сумма основного долга;
• срок просрочки по обязательству (дата возникновения просрочки и дата предполагаемого (или состоявшегося) ее погашения);
• федеральный округ, в котором находится кредитор.

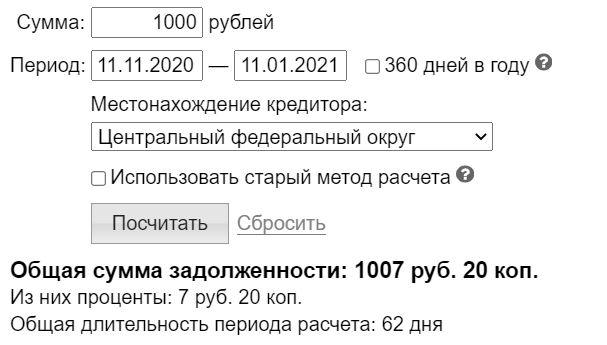
Эту информацию введите в соответствующие поля. Рассмотрим на простом примере, как рассчитать задолженность по кредиту с помощью онлайн-инструмента.

1. Представим, что основная задолженность по договору составляет 1000 рублей.

2. Просрочка возникла 11.11.2020.

Обратите внимание, что пункт «360 дней в году» в калькуляторе используется, только если задолженность образовалась в период до 24.03.2016, когда для расчета применялись периоды 360 дней в году и 30 дней в месяце. После этой даты галочку в этом окне ставить не нужно.

3. Должник и кредитор проживают в Центральном федеральном округе, поэтому выбираем его.

4. После ввода этой информации начинается непосредственный расчет неустойки по договору на калькуляторе онлайн. Результат включает общую сумму просроченного обязательства и проценты.

Обратите внимание, что итог включает:

• долг в рублях и копейках с учетом процентов;
• отдельно размер неустойки по этому долгу в денежном выражении;
• порядок расчета неустойки в деталях.

То есть будут не просто определены общие проценты, но и в разбивке по месяцам и дням, с указанием примененных процентных ставок. Эта информация необходима для составления претензии должнику и написания иска в суд.

Если в расчетный период ставка ЦБ менялась, калькулятор долга по расписке учтет это в расчете.

При необходимости инструментом просто воспользоваться для вычисления долга и суммы неустойки по старым правилам, когда применялась ставка рефинансирования ЦБ РФ. Чтобы рассчитать задолженность по договору «старым способом», достаточно поставить галочку около фразы «Использовать старый метод расчета».

Также выполненный результат легко распечатать. Для этого в него встроена удобная опция «Для печати», которая автоматически выводит полученный результат на принтер (например, для предоставления в суд или должнику).

Почему важно считать кредит самому?

Кредитами сейчас сложно кого-то удивить. Каждый среднестатистический россиянин имеет или имел как минимум один-два кредита в своей жизни или собирается его взять. Если вы идете в банк для получения кредита и вам дают несколько предложений, то нужно выбрать самое дешевое и выгодное для вас. Для этого нужно рассчитать кредит самому, например в Excel. Нужно также знать размер ежемесячного платежа, чтоб понять нагрузку займа на ваш бюджет. Это тоже можно сделать самостоятельно.

Видео

Как рассчитать годовые проценты по кредиту?

Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:

10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.

При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.

То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.

При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.

Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.

Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.

Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.

Как самостоятельно рассчитать аннуитетный платеж

Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.

Стандартная формула расчета аннуитетного платежа выглядит так:

Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.

А вот как рассчитывается коэффициент аннуитета:

Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.

Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.

Количество платежей равно количеству месяцев — 18.

Подставляем данные в формулу и считаем коэффициент аннуитета:

0,0125 × (1 + 0,0125)¹⁸ / ((1 + 0,0125)¹⁸ − 1) = 0,062385

Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.

Какие данные нужны для расчета платежа по кредиту

Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.

Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:

• ставка,
• размер желаемого займа,
• срок, на который вы хотите занять деньги.

Воспользуемся банковскими калькуляторами

Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.

Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.

Виды ежемесячных выплат по кредитам

Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.

Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.

В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.

Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.

Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.

Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.

Самостоятельный подсчет при аннуитетных платежах

Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:

1. Процентная ставка — 18%.
2. Период кредитования — 24 месяца.
3. Сумма кредита — 500000 рублей.

Классическая формула для расчета аннуитетного платежа выглядит так:

Разовый аннуитетный платеж = Сумма кредита * Ка

где Ка — это коэффициент аннуитета.

Ка = ((ЕПС* (1 + ЕПС)ⁿ)/( (1 + ЕПС)ⁿ -1)

где ЕПС — ежемесячная процентная ставка.

Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.

Итоговый расчет примет вид:

500 000 * (0,015 * (1 + 0,015)²⁴)/((1 + 0,015)²⁴ -1) = 24 962,05 рублей в месяц.

Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.

Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:

24 962,05 * 24 = 599 089,24 рублей.

Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.

Из чего состоит ежемесячный платеж

Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.

Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.

Формула расчета процентов по кредиту

S = (s₃ x i x Kk / Kr) / 100

• S = вычисляемые проценты;
• S₃ = общая сумма кредита;
• i = процентная ставка по кредиту;
• Kk = кол-во дней по платежам;
• Kr = кол-во дней на календарный год.

Какие данные нужны для расчета

• Сумма, выданная в кредит;
• Процентная ставка за год;
• Кол-во календарных дней в текущем году.

Пример расчета процентов по кредиту

65000 рублей – сумма переплаты в год. Для того чтобы посчитать сумму переплаты в месяц нужно 65000 рублей разделить на 12.

Погашать долг можно по-разному

Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.

С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.

Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.

Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.

Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).

, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.

Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.

Как составить график платежей

Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.

Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.

Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.

При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р.

В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.

Сначала считаем проценты:

Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году

Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р.

Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р.

Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р.

На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).

Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.

График выплаты кредита с аннуитетными платежами

Номер платежа	Сумма платежа	Сумма в погашение тела кредита	Сумма платежа в погашение процентов	Остаток долга
1	18 715,44	15 016,81	3698,63	284 983,19
2	18 715,44	15 084,83	3630,61	269 898,37
3	18 715,44	15 387,92	3327,51	254 510,44
4	18 715,44	15 473,04	3242,39	239 037,40
5	18 715,44	15 670,17	3045,27	223 367,24
6	18 715,44	16 053,39	2662,05	207 313,85
7	18 715,44	16 074,31	2641,12	191 239,53
8	18 715,44	16 357,69	2357,75	174 881,84
9	18 715,44	16 487,49	2227,95	158 394,35
10	18 715,44	16 762,63	1952,81	141 631,73
11	18 715,44	16 911,09	1804,35	124 720,64
12	18 715,44	17 126,53	1588,91	107 594,11
13	18 715,44	17 388,93	1326,50	90 205,18
14	18 715,44	17 566,25	1149,19	72 638,93
15	18 715,44	17 819,89	895,55	54 819,04
16	18 715,44	18 017,06	698,38	36 801,98
17	18 715,44	18 246,59	468,85	18 555,40
18	18 768,91	18 555,39	213,51

Первый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 016,81

Сумма платежа в погашение процентов

3698,63

Остаток долга 284 983,19

Второй платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 084,83

Сумма платежа в погашение процентов

3630,61

Остаток долга 269 898,37

Третий платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 387,92

Сумма платежа в погашение процентов

3327,51

Остаток долга 254 510,44

Четвертый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 473,04

Сумма платежа в погашение процентов

3242,39

Остаток долга 239 037,40

Пятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 670,17

Сумма платежа в погашение процентов

3045,27

Остаток долга 223 367,24

Шестой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 053,39

Сумма платежа в погашение процентов

2662,05

Остаток долга 207 313,85

Седьмой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 074,31

Сумма платежа в погашение процентов

2641,12

Остаток долга 191 239,53

Восьмой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 357,69

Сумма платежа в погашение процентов

2357,75

Остаток долга 174 881,84

Девятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 487,49

Сумма платежа в погашение процентов

2227,95

Остаток долга 158 394,35

Десятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 762,63

Сумма платежа в погашение процентов

1952,81

Остаток долга 141 631,73

Одиннадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 911,09

Сумма платежа в погашение процентов

1804,35

Остаток долга 124 720,64

Двенадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 126,53

Сумма платежа в погашение процентов

1588,91

Остаток долга 107 594,11

Тринадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 388,93

Сумма платежа в погашение процентов

1326,50

Остаток долга 90 205,18

Четырнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 566,25

Сумма платежа в погашение процентов

1149,19

Остаток долга 72 638,93

Пятнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 819,89

Сумма платежа в погашение процентов

895,55

Остаток долга 54 819,04

Шестнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

18 017,06

Сумма платежа в погашение процентов

698,38

Остаток долга 36 801,98

Семнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

18 246,59

Сумма платежа в погашение процентов

468,85

Остаток долга 18 555,40

Восемнадцатый платеж Сумма платежа 18 768,91 Сумма в погашение тела кредита 18 555,39 Сумма платежа в погашение процентов 213,51 Остаток долга

При дифференцированном платеже проценты в первом месяце будут такими же — 3698,63 Р. Дальше же принцип расчета процентов аналогичен, а сумма основного долга будет каждый месяц уменьшаться равномерно — на 16 666,67 Р (300 000 / 18). Ежемесячный платеж будет складываться из этих двух сумм.

В результате в первые месяцы платеж будет больше, чем при аннуитетном способе, а итоговая переплата будет меньше.

График выплаты кредита с дифференцированными платежами

Номер платежа	Сумма платежа	Сумма в погашение тела кредита	Сумма платежа в погашение процентов	Остаток долга
1	20 365,30	16 666,67	3698,63	283 333,33
2	20 276,26	16 666,67	3609,59	266 666,67
3	19 954,34	16 666,67	3287,67	250 000,00
4	19 851,60	16 666,67	3184,93	233 333,33
5	19 639,27	16 666,67	2972,60	216 666,67
6	19 248,86	16 666,67	2582,19	200 000,00
7	19 214,61	16 666,67	2547,95	183 333,33
8	18 926,94	16 666,67	2260,27	166 666,67
9	18 789,95	16 666,67	2123,29	150 000,00
10	18 515,98	16 666,67	1849,32	133 333,33
11	18 365,30	16 666,67	1698,63	116 666,67
12	18 152,97	16 666,67	1486,30	100 000,00
13	17 899,54	16 666,67	1232,88	83 333,33
14	17 728,31	16 666,67	1061,64	66 666,67
15	17 488,58	16 666,67	821,92	50 000,00
16	17 303,65	16 666,67	636,99	33 333,33
17	17 091,32	16 666,67	424,66	16 666,67
18	16 858,45	16 666,67	191,78

Первый платеж

Сумма платежа

20 365,30

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3698,63

Остаток долга 283 333,33

Второй платеж

Сумма платежа

20 276,26

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3609,59

Остаток долга 266 666,67

Третий платеж

Сумма платежа

19 954,34

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3287,67

Остаток долга 250 000,00

Четвертый платеж

Сумма платежа

19 851,60

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3184,93

Остаток долга 233 333,33

Пятый платеж

Сумма платежа

19 639,27

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2972,60

Остаток долга 216 666,67

Шестой платеж

Сумма платежа

19 248,86

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2582,19

Остаток долга 200 000,00

Седьмой платеж

Сумма платежа

19 214,61

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2547,95

Остаток долга 183 333,33

Восьмой платеж

Сумма платежа

18 926,94

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2260,27

Остаток долга 166 666,67

Девятый платеж

Сумма платежа

18 789,95

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2123,29

Остаток долга 150 000,00

Десятый платеж

Сумма платежа

18 515,98

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1849,32

Остаток долга 133 333,33

Одиннадцатый платеж

Сумма платежа

18 365,30

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1698,63

Остаток долга 116 666,67

Двенадцатый платеж

Сумма платежа

18 152,97

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1486,30

Остаток долга 100 000,00

Тринадцатый платеж

Сумма платежа

17 899,54

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1232,88

Остаток долга 83 333,33

Четырнадцатый платеж

Сумма платежа

17 728,31

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1061,64

Остаток долга 66 666,67

Пятнадцатый платеж

Сумма платежа

17 488,58

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

821,92

Остаток долга 50 000,00

Шестнадцатый платеж

Сумма платежа

17 303,65

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

636,99

Остаток долга 33 333,33

Семнадцатый платеж

Сумма платежа

17 091,32

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

424,66

Остаток долга 16 666,67

Восемнадцатый платеж Сумма платежа 16 858,45 Сумма в погашение тела кредита 16 666,67 Сумма платежа в погашение процентов 191,78 Остаток долга

Теги