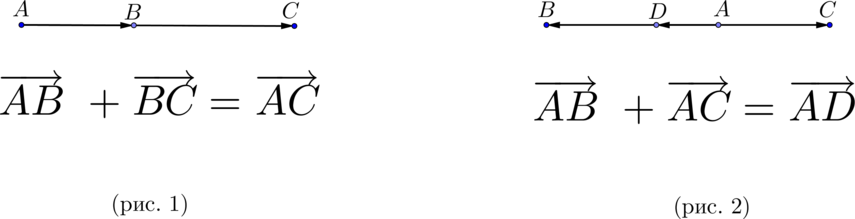Как найти сумму одного вектора - Сайт, где вы сможете решить свои вопросы

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Векторы: правила сложения и вычитания

Вектор (overrightarrow{AB}) можно рассматривать как перемещение точки из положения (A) (начало движения) в положение (B) (конец движения). То есть траектория движения в этом случае не важна, важны только начало и конец!

(blacktriangleright) Два вектора коллинеарны, если они лежат на одной прямой или на двух параллельных прямых.
В противном случае векторы называются неколлинеарными.

(blacktriangleright) Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
Если их направления противоположны, то они называются противоположно направленными.

Правила сложения коллинеарных векторов:

(blacktriangleright) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

(blacktriangleright) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

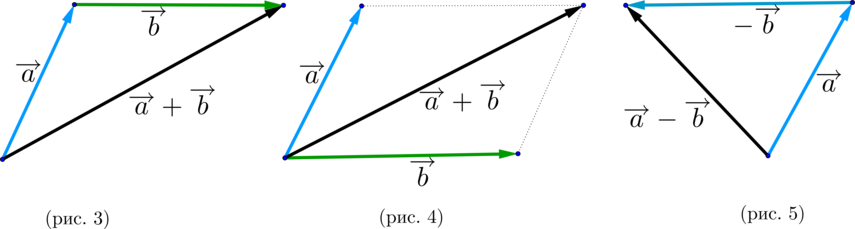
Правила сложения неколлинеарных векторов (overrightarrow
{a}) и (overrightarrow{b}):

(blacktriangleright) Правило треугольника (рис. 3).

Нужно от конца вектора (overrightarrow {a}) отложить вектор (overrightarrow {b}). Тогда сумма (overrightarrow
{a}+overrightarrow {b}) – это вектор, начало которого совпадает с началом вектора (overrightarrow
{a}), а конец – с концом вектора (overrightarrow {b}).

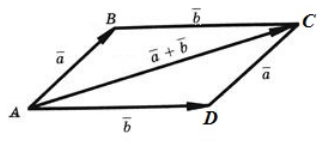
(blacktriangleright) Правило параллелограмма (рис. 4).

Нужно от начала вектора (overrightarrow {a}) отложить вектор (overrightarrow {b}). Тогда сумма (overrightarrow
{a}+overrightarrow {b}) – вектор, совпадающей с диагональю параллелограмма, построенного на векторах (overrightarrow {a}) и (overrightarrow {b}) (начало которого совпадает с началом обоих векторов).

(blacktriangleright) Для того, чтобы найти разность двух векторов (overrightarrow {a}-overrightarrow{b}), нужно найти сумму векторов (overrightarrow {a}) и (-overrightarrow{b}): (overrightarrow{a}-overrightarrow{b}=overrightarrow{a}+(-overrightarrow{b})) (рис. 5).

Задание
1

#2638

Уровень задания: Сложнее ЕГЭ

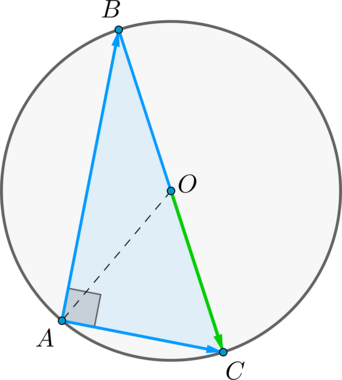
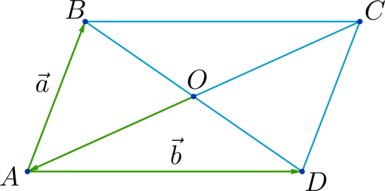
Дан прямоугольный треугольник (ABC) с прямым углом (A), точка (O) – центр описанной около данного треугольника окружности. Координаты вектора (overrightarrow{AB}={1;1}), (overrightarrow{AC}={-1;1}). Найдите сумму координат вектора (overrightarrow{OC}).

Т.к. треугольник (ABC) — прямоугольный, то центр описанной окружности лежит на середине гипотенузы, т.е. (O) — середина (BC).

Заметим, что (overrightarrow{BC}=overrightarrow{AC}-overrightarrow{AB}), следовательно, (overrightarrow{BC}={-1-1;1-1}={-2;0}).

Т.к. (overrightarrow{OC}=dfrac12 overrightarrow{BC}), то (overrightarrow{OC}={-1;0}).

Значит, сумма координат вектора (overrightarrow{OC}) равна (-1+0=-1).

Ответ: -1

Задание
2

#674

Уровень задания: Сложнее ЕГЭ

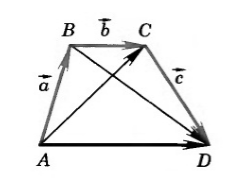
(ABCD) – четырёхугольник, на сторонах которого отложены векторы (overrightarrow{AB}), (overrightarrow{BC}), (overrightarrow{CD}), (overrightarrow{DA}). Найдите длину вектора (overrightarrow{AB} + overrightarrow{BC} + overrightarrow{CD} + overrightarrow{DA}).

(overrightarrow{AB} + overrightarrow{BC} = overrightarrow{AC}), (overrightarrow{AC} + overrightarrow{CD} = overrightarrow{AD}), тогда
(overrightarrow{AB} + overrightarrow{BC} + overrightarrow{CD} + overrightarrow{DA} = overrightarrow{AC} + overrightarrow{CD} + overrightarrow{DA}= overrightarrow{AD} + overrightarrow{DA} = overrightarrow{AD} – overrightarrow{AD} = vec{0}).
Нулевой вектор имеет длину, равную (0).

Вектор можно воспринимать как перемещение, тогда (overrightarrow{AB} + overrightarrow{BC}) – перемещение из (A) в (B), а затем из (B) в (C) – в итоге это перемещение из (A) в (C).

При такой трактовке становится очевидным, что (overrightarrow{AB} + overrightarrow{BC} + overrightarrow{CD} + overrightarrow{DA} = vec{0}), ведь в итоге здесь из точки (A) переместились в точку (A), то есть длина такого перемещения равна (0), значит, и сам вектор такого перемещения есть (vec{0}).

Ответ: 0

Задание
3

#1805

Уровень задания: Сложнее ЕГЭ

Дан параллелограмм (ABCD). Диагонали (AC) и (BD) пересекаются в точке (O). Пусть (overrightarrow{AB} = vec{a}), (overrightarrow{AD} = vec{b}), тогда (overrightarrow{OA} = xcdotvec{a} + ycdotvec{b}), где (x) и (y) – некоторые числа. Найдите число, равное (x + y).

[overrightarrow{OA} = frac{1}{2}overrightarrow{CA} = frac{1}{2}(overrightarrow{CB} + overrightarrow{BA}) = frac{1}{2}(overrightarrow{DA} + overrightarrow{BA}) = frac{1}{2}(-vec{b} – vec{a}) = – frac{1}{2}vec{a} – frac{1}{2}vec{b}] (Rightarrow) (x = – frac{1}{2}), (y = – frac{1}{2}) (Rightarrow) (x + y = -1).

Ответ: -1

Задание
4

#1806

Уровень задания: Сложнее ЕГЭ

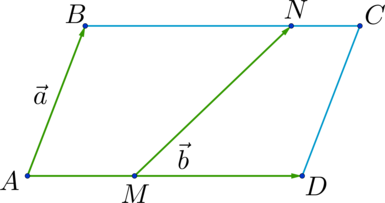
Дан параллелограмм (ABCD). Точки (K) и (L) лежат на сторонах (BC) и (CD) соответственно, причем (BK:KC = 3:1), а (L) – середина (CD). Пусть (overrightarrow{AB} = vec{a}), (overrightarrow{AD} = vec{b}), тогда (overrightarrow{KL} = xcdotvec{a} + ycdotvec{b}), где (x) и (y) – некоторые числа. Найдите число, равное (x + y).

[overrightarrow{KL} = overrightarrow{KC} + overrightarrow{CL} = frac{1}{4}overrightarrow{BC} + frac{1}{2}overrightarrow{CD} = frac{1}{4}overrightarrow{AD} + frac{1}{2}overrightarrow{BA} = frac{1}{4}vec{b} – frac{1}{2}vec{a}] (Rightarrow) (x = -frac{1}{2}), (y = frac{1}{4}) (Rightarrow) (x + y = -0,25).

Ответ: -0,25

Задание
5

#1807

Уровень задания: Сложнее ЕГЭ

Дан параллелограмм (ABCD). Точки (M) и (N) лежат на сторонах (AD) и (BC) соответственно, причем (AM:MD = 2:3), а (BN:NC = 3:1). Пусть (overrightarrow{AB} = vec{a}), (overrightarrow{AD} = vec{b}), тогда (overrightarrow{MN} = xcdotvec{a} + ycdotvec{b}), где (x) и (y) – некоторые числа. Найдите число, равное (xcdot y).

[overrightarrow{MN} = overrightarrow{MA} + overrightarrow{AB} + overrightarrow{BN} = frac{2}{5}overrightarrow{DA} + overrightarrow{AB} + frac{3}{4}overrightarrow{BC} = – frac{2}{5}overrightarrow{AD} + overrightarrow{AB} + frac{3}{4}overrightarrow{BC} = -frac{2}{5}vec{b} + vec{a} + frac{3}{4}vec{b} = vec{a} + frac{7}{20}vec{b}] (Rightarrow) (x = 1), (y = frac{7}{20}) (Rightarrow) (xcdot y = 0,35).

Ответ: 0,35

Задание
6

#1808

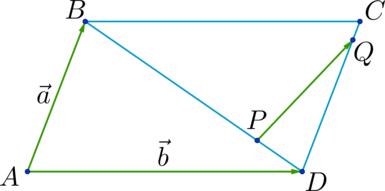
Уровень задания: Сложнее ЕГЭ

Дан параллелограмм (ABCD). Точки (P) лежит на диагонали (BD), точка (Q) лежит на стороне (CD), причем (BP:PD = 4:1), а (CQ:QD = 1:9). Пусть (overrightarrow{AB} = vec{a}), (overrightarrow{AD} = vec{b}), тогда (overrightarrow{PQ} = xcdotvec{a} + ycdotvec{b}), где (x) и (y) – некоторые числа. Найдите число, равное (xcdot y).

[begin{gathered}
overrightarrow{PQ} = overrightarrow{PD} + overrightarrow{DQ} = frac{1}{5}overrightarrow{BD} + frac{9}{10}overrightarrow{DC} = frac{1}{5}(overrightarrow{BC} + overrightarrow{CD}) + frac{9}{10}overrightarrow{AB} =\
= frac{1}{5}(overrightarrow{AD} + overrightarrow{BA}) + frac{9}{10}overrightarrow{AB} = frac{1}{5}(overrightarrow{AD} – overrightarrow{AB}) + frac{9}{10}overrightarrow{AB} = frac{1}{5}overrightarrow{AD} + frac{7}{10}overrightarrow{AB} = frac{1}{5}vec{b} + frac{7}{10}vec{a}end{gathered}]

(Rightarrow) (x = frac{7}{10}), (y = frac{1}{5}) (Rightarrow) (xcdot y = 0,14).

Ответ: 0,14

Задание
7

#1809

Уровень задания: Сложнее ЕГЭ

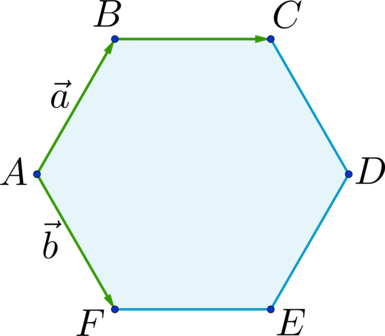
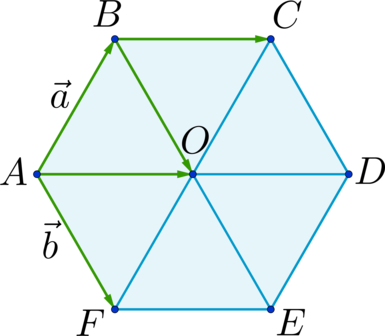
Дан правильный шестиугольник (ABCDEF). Пусть (overrightarrow{AB} = vec{a}), (overrightarrow{AF} = vec{b}), тогда (overrightarrow{BC} = xcdotvec{a} + ycdotvec{b}), где (x) и (y) – некоторые числа. Найдите число, равное (x + y).

Отрезки (AD), (BE) и (CF) пересекаются в точке (O) и делятся этой точкой пополам. (BC parallel AD) и (ABCO) – параллелограмм; (AF parallel BE) и (ABOF) – параллелограмм (Rightarrow) [overrightarrow{BC} = overrightarrow{AO} = overrightarrow{AB} + overrightarrow{BO} = overrightarrow{AB} + overrightarrow{AF} = vec{a} + vec{b}] (Rightarrow) (x = 1), (y = 1) (Rightarrow) (x + y = 2).

Ответ: 2

Старшеклассники, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение достойных баллов, обязательно должны повторить тему «Правила сложения и вычитания нескольких векторов». Как видно из многолетней практики, подобные задания каждый год включаются в аттестационное испытание. Если у выпускника вызывают трудности задачи из раздела «Геометрия на плоскости», к примеру, в которых требуется применить правила сложения и вычитания векторов, ему обязательно стоит повторить или вновь разобраться в материале, чтобы успешно сдать ЕГЭ.

Образовательный проект «Школково» предлагает новый подход в подготовке к аттестационному испытанию. Наш ресурс выстроен таким образом, чтобы учащиеся смогли выявить наиболее сложные для себя разделы и восполнить пробелы в знаниях. Специалисты «Школково» подготовили и систематизировали весь необходимый материал для подготовки к сдаче аттестационного испытания.

Для того чтобы задачи ЕГЭ, в которых необходимо применить правила сложения и вычитания двух векторов, не вызывали затруднений, мы рекомендуем прежде всего освежить в памяти базовые понятия. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».

Если вы уже вспомнили правило вычитания векторов и основные определения по данной теме, предлагаем закрепить полученные знания, выполнив соответствующие упражнения, которые подобрали специалисты образовательного портала «Школково». Для каждой задачи на сайте представлен алгоритм решения и дан правильный ответ. В теме «Правила сложения векторов» представлены различные упражнения; выполнив два-три сравнительно легких задания, учащиеся могут последовательно переходить к более сложным.

Оттачивать собственные навыки по таким, например, заданиям, как задачи на координатной плоскости, школьники имеют возможность в режиме онлайн, находясь в Москве или любом другом городе России. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

УСТАЛ? Просто отдохни

Источник

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
Разность векторов
- Формула вычитания векторов
Примеры задач

Сумма векторов

Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c, начало которого совпадает с началом a, а конец – с концом b. При этом конец вектора a должен совпадать с началом вектора b.

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c, совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

c_i = a_i + b_i

Элементы вектора c равняются попарной сумме соответствующих элементов a и b.


Для плоских задач	a + b = {a_x + b_x; a_y + b_y}
Для трехмерных задач	a + b = {a_x + b_x; a_y + b_y; a_z + b_z}
Для n-мерных векторов	a + b = {a₁ + b₁; a₂ + b₂; … a_n + b_n}

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: (a + b) + c = a + (b + c)

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (-a) = 0

Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b, то получится c, причем должно соблюдаться условие: b + c = a

Формула вычитания векторов

c_i = a_i – b_i

Элементы вектора c равны попарной разности соответствующих элементов a и b.


Для плоских задач	a – b = {a_x – b_x; a_y – b_y}
Для трехмерных задач	a – b = {a_x – b_x; a_y – b_y; a_z – b_z}
Для n-мерных векторов	a – b = {a₁ – b₁; a₂ – b₂; … a_n – b_n}

Примеры задач

Задание 1
Вычислим сумму векторов a = {3; 5} и b = {2; 7}.

Решение:
a + b = {3 + 2; 5 + 7} = {5; 12}.

Задание 2
Найдем разность векторов a = {4; 8; -2} и b = {-1; 9; 5}.

Решение:
a – b = {4 – (-1); 8 – 9; -2 – 5} = {5; -1; -7}.

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Откладывание вектора от данной точки

Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

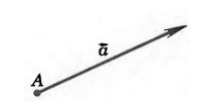
Определение 1

Если точка $A$ начала какого-либо вектора $overrightarrow{a}$, то говорят, что вектор $overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $overrightarrow{a}$ отложенный от точки $A$

Введем следующую теорему:

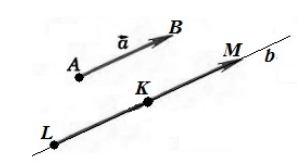
От любой точки $K$ можно отложить вектор $overrightarrow{a}$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

Вектор $overrightarrow{a}$ – нулевой.

В этом случае, очевидно, что искомый вектор — вектор $overrightarrow{KK}$.
Вектор $overrightarrow{a}$ – ненулевой.

Обозначим точкой $A$ начало вектора $overrightarrow{a}$, а точкой $B$ – конец вектора $overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $overrightarrow{a}$. Отложим на этой прямой отрезки $left|KLright|=|AB|$ и $left|KMright|=|AB|$. Рассмотрим векторы $overrightarrow{KL}$ и $overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $overrightarrow{a}$ (рис. 2)

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Сложение векторов. Правило треугольника

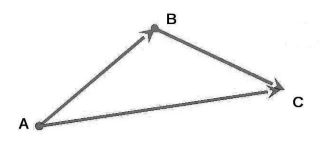
Пусть нам даны векторы $overrightarrow{a}$ и $overrightarrow{b}$.

Определение 2

Суммой векторов $overrightarrow{a}+overrightarrow{b}$ называется вектор $overrightarrow{c}=overrightarrow{AC}$, построенный следующим образом: От произвольной точки $A$ отклабывается вектор $overrightarrow{AB}=overrightarrow{a}$, затем от полученной точки $B$ откладывается вектор $overrightarrow{BC}=overrightarrow{b}$ и соединяют точку $A$ c точкой $C$ (рис. 3).

Рисунок 3. Сумма векторов

«Сложение векторов. Как найти сумму векторов» 👇

Замечание 1

Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.

Из этого правила следует несколько свойств сложения двух векторов:

Для любого вектора $overrightarrow{a}$ выполняется равенство

[overrightarrow{a}+overrightarrow{0}=overrightarrow{a}]
Для любых произвольных точек $A, B и C$ выполняется равенство

[overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}]

Замечание 2

Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.

Правило параллелограмма

Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.

Теорема 2

Для любых треух векторов $overrightarrow{a}, overrightarrow{b} и overrightarrow{c}$ справедливы следующие два закона:

Переместительный закон:

[overrightarrow{a}+overrightarrow{b}=overrightarrow{b}+overrightarrow{a}]

Сочетательный закон:

[left(overrightarrow{a}+overrightarrow{b}right)+overrightarrow{c}=overrightarrow{a}+left(overrightarrow{b}+overrightarrow{c}right)]

Доказательство.

Переместительный закон:

Пусть векторы $overrightarrow{a} и overrightarrow{b}$ не коллинеарны.

Возьмем произвольную точку $A$ и построим от нее (на одном рисунке) суммы $overrightarrow{a}+overrightarrow{b} и overrightarrow{b}+overrightarrow{a}$. Получим следующий рисунок (рис 4).

Рисунок 4. Иллюстрация переместительного закона

Очевидно, что $overrightarrow{a}+overrightarrow{b}=overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, а $overrightarrow{b}+overrightarrow{a}=overrightarrow{AD}+overrightarrow{DC}=overrightarrow{AC}$

Следовательно, $overrightarrow{a}+overrightarrow{b}=overrightarrow{b}+overrightarrow{a}$.
Пусть векторы $overrightarrow{a} и overrightarrow{b}$ коллинеарны.

Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $left|overrightarrow{a}+overrightarrow{b}right|и |overrightarrow{b}+overrightarrow{a}|$.

Сочетательный закон:

Построим следующий рисунок: Отложим от произвольной точки $A$ вектор $overrightarrow{AB}=overrightarrow{a}$, от полученной точки $B$ — вектор $overrightarrow{BC}=overrightarrow{b}$ и от точки $C$ — вектор $overrightarrow{CD}=overrightarrow{c}$ (Рис. 5).

Рисунок 5. Иллюстрация сочетательного закона

Из свойства правила треугольника $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:

Следовательно, $left(overrightarrow{a}+overrightarrow{b}right)+overrightarrow{c}=overrightarrow{a}+left(overrightarrow{b}+overrightarrow{c}right)$.

Теорема доказана.

Из этой теоремы мы теперь можем выделить правило параллелограмма для суммы двух неколлинеарных векторов: чтобы сложить два неколлинеарных вектора $overrightarrow{a}$ и $overrightarrow{b}$, нужно отложить от произвольной точки $A$ векторы $overrightarrow{AB}=overrightarrow{a}$ и $overrightarrow{AD}=overrightarrow{b}$ и построить параллелограмм $ABCD$. Тогда $overrightarrow{a}+overrightarrow{b}=overrightarrow{AC}$.

Пример задачи на сложение векторов

Пример 1

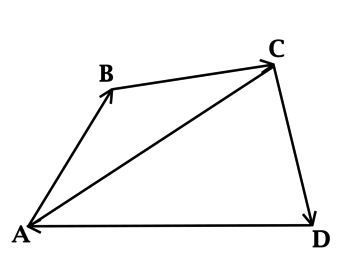
Дан четырехугольник $ABCD$. Доказать, что $overrightarrow{AB}+overrightarrow{BC}+overrightarrow{CD}=overrightarrow{AD}$

Рисунок 6.

Доказательство.

Воспользуемся свойством правила треугольника $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:

[overrightarrow{AB}+overrightarrow{BC}+overrightarrow{CD}=overrightarrow{AC}+overrightarrow{CD}=overrightarrow{AD}]

ч. т. д.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Содержание:

Формула
Примеры нахождения суммы векторов

Формула

Чтобы найти сумму векторов $bar{a}+bar{b}$, которые заданны координатами
$bar{a}=(a_x;a_y)$ и $bar{b}=(b_x;b_y)$, необходимо сложить соответствующие
координаты этих векторов,
то есть

$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y}right)$$

В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их сумма равна

$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y} ; a_{z}+b_{z}right)$$

Примеры нахождения суммы векторов

Пример

Задание. Найти сумму векторов
$bar{a}+bar{b}$,
$bar{a}=(2;0)$ и
$bar{b}=(1;3)$

Решение. Для нахождения суммы векторов, сложим их соответствующие координаты

$$bar{a}+bar{b}=(2 ; 0)+(1 ; 3)=(2+1 ; 0+3)=(3 ; 3)$$

Ответ. $bar{a}+bar{b}==(3 ; 3)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти суммы векторов
$bar{a}+bar{b}$,
$bar{a}+bar{c}$,
$bar{b}+bar{c}$ и
$bar{a}+bar{b} +bar{c}$, если
$bar{a}=(1;-1;0)$,
$bar{b}=(3;2;-1)$ и
$bar{c}=(4;2;-1)$

Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:

$$bar{a}+bar{b}=(1+3 ;-1+2 ; 0+(-2))=(4 ; 1 ;-2)$$
$$bar{a}+bar{c}=(1+4 ;-1+2 ; 0+(-1))=(5 ; 1 ;-1)$$
$$bar{b}+bar{c}=(3+4 ; 2+2 ;-2+(-1))=(7 ; 4 ;-3)$$
$$bar{a}+bar{b}+bar{c}=(1+3+4 ;-1+2+2 ; 0+(-2)+(-1))=(8 ; 3 ;-3)$$

Ответ. $bar{a}+bar{b}=(4 ; 1 ;-2)$ , $bar{a}+bar{c}=(5 ; 1 ;-1)$ , $bar{b}+bar{c}=(7 ; 4 ;-3)$ , $bar{a}+bar{b}+bar{c}=(8 ; 3 ;-3)$

Читать дальше: как найти разность векторов.

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Сложение векторов

Формула

Чтобы складывать вектора нужно найти суммы соответствующих координат данных векторов. Например, пусть есть векторы на плоскости $ overline{a} = (x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, тогда их сумму можно найти по формуле: $$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2)$$

Если векторы заданы в пространстве тремя координатами $ overline{a} = (x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то выполнить сложение нужно по другой формуле:

$$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2; z_1+z_2) $$

При сложении первая координата первого вектора складывается с первой координатой второго вектора, вторая координата первого вектора складывается со второй координатой второго вектора и так далее в зависимости от размерности векторов. Стоит отметить, что складывать векторы можно только одинаковой размерности.

Примеры решений

Пример

Даны два вектора $ overline{a} = (1,3) $ и $ overline{b} = (2,4) $. Нужно сложить два вектора.

Решение

Итак, как складывать вектора по координатам? К первой прибавляем первую, вторую ко второй:

$$ overline{a}+overline{b} = (1+2;3+4) = (3;7) $$

В этой задаче векторы заданы в двумерном пространстве и имеют только две координаты. Если бы координат было бы три, то применять нужно вторую формулу для трехмерной задачи.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a}+overline{b} = (3;7) $$

Источник

Векторы: правила сложения и вычитания

Сумма векторов

Формула сложения векторов

Свойства сложения векторов

Разность векторов

Формула вычитания векторов

Примеры задач

Откладывание вектора от данной точки

Сложение векторов. Правило треугольника

Правило параллелограмма

Пример задачи на сложение векторов

Формула

Примеры нахождения суммы векторов

Сложение векторов

Формула

Примеры решений

Вам также может понравиться

Как найти работу бросания

Windows 7 как найти видео файлы

Как подключить функцию найти телефон

Добавить комментарий Отменить ответ