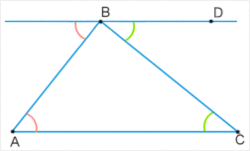
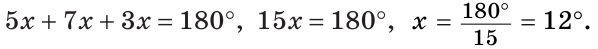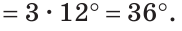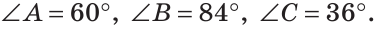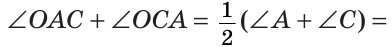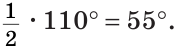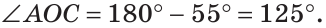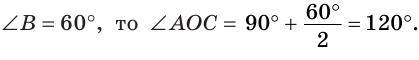Сумма углов треугольника равна (180°).
Доказательство
Рассмотрим произвольный треугольник (KLM) и докажем, что
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
1. Через вершину (L) параллельно стороне (KM) проведём прямую (a).
2. При пересечении параллельных прямых (a) и (KM) секущей (KL), углы, которые обозначаются (1), будут накрест лежащими углами, а углы, обозначенные (2) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е.
∠
(1) (+)
∠
(2) (+)
∠
(3 =)
180°
, или
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна
90°
.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен
45°
.
Следствие 3. В равностороннем треугольнике каждый угол равен
60°
.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказательство
Из равенств
∠
(KML) (+)
∠
(BML=)
180°
и
∠
(K) (+)
∠
(L) (+)
∠
(KML =)
180°
получаем, что
∠
(BML =)
∠
(K) (+)
∠
(L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
У треугольника (KLM) все углы острые.
У треугольника (KMN) угол (K = 90)
°
.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.
У треугольника (KLM) один угол тупой.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 марта 2023 года; проверки требуют 6 правок.
Теорема о сумме углов треугольника — классическая теорема евклидовой геометрии.
Формулировка[править | править код]
Сумма углов любого треугольника на евклидовой плоскости равна 180°.[1]
Доказательство[править | править код]
Пусть 
Следствия[править | править код]
- В треугольнике не может быть двух тупых или двух прямых углов, потому что тогда сумма углов была бы больше 180°. По той же причине треугольник не может содержать тупой и прямой углы одновременно.
- У любого треугольника не меньше двух острых углов. Действительно, случай, когда у треугольника только один острый угол или вообще нет острых углов, противоречит предыдущему следствию.
- В прямоугольном треугольнике оба угла при гипотенузе — острые.
- В равнобедренном треугольнике углы при основании равны, поэтому тупым может быть только угол, противолежащий основанию.
- В равнобедренном прямоугольном треугольнике углы при гипотенузе равны (180° — 90°) /2 = 45°.
- В равностороннем треугольнике все три угла совпадают и поэтому равны 180° / 3 = 60°.
- (Теорема о внешнем угле треугольника) Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним[2].
Вариации и обобщения[править | править код]
Многоугольники[править | править код]
Обобщение для симплексов[править | править код]
Существует более сложное соотношение между двугранными углами произвольного симплекса. А именно, если 
.
Это следует из того, что этот определитель является определителем Грама нормалей к граням симплекса, а определитель Грама линейно зависимых векторов равен 0, и 

В неевклидовых геометриях[править | править код]
Приведённое в этой статье доказательство опирается на определённое свойство параллельных прямых, а именно — утверждение о том, что внутренние накрест лежащие углы при параллельных прямых равны. Доказательство этого утверждения, в свою очередь, использует аксиому параллельности евклидовой геометрии. Можно показать, что любое доказательство теоремы о сумме углов треугольника будет использовать аксиому параллельности, и наоборот — из утверждения, что сумма углов треугольника равна 180°, можно вывести аксиому параллельности, если даны остальные аксиомы классической геометрии (абсолютная геометрия)[3].
Таким образом, равенство суммы углов треугольника 180° является одним из основных признаков именно евклидовой геометрии, отличающих её от неевклидовых, в которых аксиома параллельности не выполняется:
- На сфере сумма углов треугольника всегда превышает 180°, разница называется сферическим избытком и пропорциональна площади треугольника. У сферического треугольника могут быть два или даже три прямых или тупых угла.
-
- Пример. Одна вершина треугольника на сфере — северный полюс. Этот угол может иметь значение до 180°. Две другие вершины лежат на экваторе, соответствующие углы равны 90°.
- В геометрии Лобачевского сумма углов треугольника всегда меньше 180° и может быть сколь угодно малой. Разность также пропорциональна площади треугольника.
Примечания[править | править код]
- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 81.
- ↑ Элементарная математика, 1976, с. 421.
- ↑ Лелон-Ферран Ж. Основания геометрии. — М.: Мир, 1989. — С. 255—256. — 312 с. — ISBN 5-03-001008-4.
Литература[править | править код]
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Сумма углов треугольника:
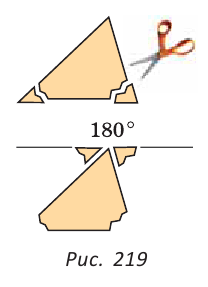
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
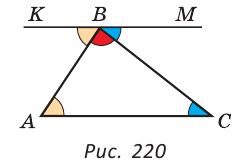
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
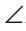
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 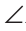
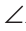
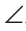





Следствия.
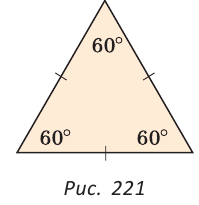
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
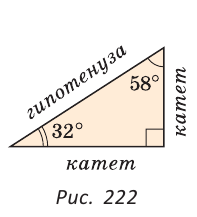
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
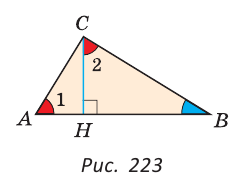
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то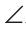
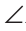
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
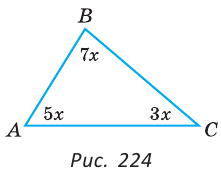
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 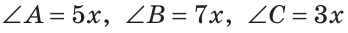
Так как сумма углов треугольника равна 180°, то
Тогда 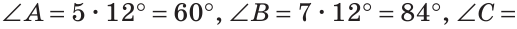
Ответ:
Пример:
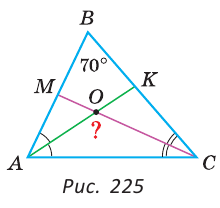
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° – 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Ответ: 125°.
Замечание. Если 
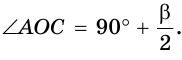
Пример:
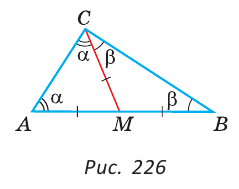
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 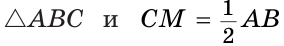
Докажем, что























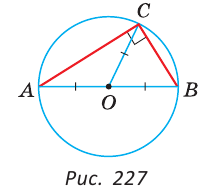
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
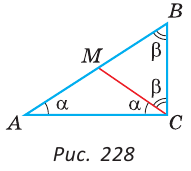
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 7 класс. Задачи на применение теоремы о сумме углов треугольника. Они встречаются в 15 задании ОГЭ по математике.
Вспомним теорему о сумме углов треугольника:
Сумма углов в треугольнике равна 180 градусам.
Задача №1
Решение
Сумма всех углов в треугольнике равна 180 градусам. Нам известны два угла в треугольнике. Они равны 72 и 42 градуса. Значит, третий угол равен:
Ответ 66
Задача №2
Решение
Отметив известный угол на чертеже. Необходимо найти внешний угол треугольника, который обозначен красным цветом.
Внешний угол треугольника – называется угол, который смежный с каким-нибудь внутренним углом этого треугольника.
Свойство смежных углов:
Смежный угол треугольника равен 180 градусам.
Рядом с чертежом треугольника сделаем смежные углы.
Теперь найдем угол, смежный с углом в 115 градусов.
Ответ 65
Задача №3
Решение
В треугольнике АВС АВ=ВС, т.е. две стороны равны. Значит треугольник равнобедренный. Третья сторона – основание.
Свойство равнобедренного треугольника:
В равнобедренном треугольнике углы при основании равны
Отметим на чертеже равные углы одинаковыми дугами и известный угол АВС.
Ответ 37
Задача №4
Решение
Прямой угол на чертеже обозначается квадратиком и равен 90 градусов.
Отметим на чертеже все известные углы
Решение задачи через теорему о сумме углов в треугольнике:
Решение задачи через свойство прямоугольного треугольника
Сумма острых углов прямоугольного треугольника равна 90 градусам
Ответ 69
Задача №5
Решение
Отметим на чертеже известные углы. Для того чтобы найти угол АВН, нужно рассмотреть треугольник АВН (прямоугольный с прямым углом АНВ=90). В решении этой задачи можно воспользоваться теоремой о сумме углов треугольника или свойством острых углов прямоугольного треугольника.
Ответ 53
Задача №6
Решение
Отметим на рисунке равные стороны, известные углы и то, что нужно найти.
Так как в треугольнике АВС стороны АС и ВС равны, то треугольник АВС равнобедренный. В равнобедренном треугольнике углы при основании равны (отмечено синими дугами).
Найдем внутренний угол треугольника при внешнем угле в 125 градусов
Вычислим угол АСВ применив теорему о сумме углов в треугольнике
Задача №7
Решение
Для решения этой задачи, нам необходимо вспомнить, что такое биссектриса и ее свойстве. Об этом было сказано здесь
Коротко: Биссектриса делит угол на две равные части. Отметим на рисунке, какие углы у нас получатся. Разделим углы М и N пополам и отметим это на чертеже.
Найдем градусную меру угла NAM по теореме о сумме углов в треугольнике
Ответ 117.
Задание №8
Решение
Отметим на чертеже известные углы и то, что надо найти.
Для решения необходимо найти еще угол ALB, смежный с углом ALC.
Теперь можно вычислить угол BAL который равен углу LAC по свойству биссектрисы угла треугольника.
Воспользуемся теоремой о сумме углов в треугольнике и вычислим угол ACB
Ответ 16.
Задача №9
Решение
Из первого предложения задачи выясняем, что треугольник ADC – равнобедренный, так как AD=AC. Отметим это на чертеже и вычислим углы при основании треугольника ADC.
Нам необходимо найти градусную меру угла DCB.
Ответ 53,5
Задача №10
Решение
Так как углы А и С известны, то можем найти угол В по теореме о сумме углов в треугольнике.
Так как BD биссектриса в треугольнике ABC, то углы ABD и CBD равны.
Рассмотрим прямоугольный треугольник CHB. В треугольнике CHB по свойству острых углов в прямоугольном треугольнике найдем острый угол СВН.
Осталось по задаче найти градусную меру угла DBH.
Ответ 20
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Сумма острых углов прямоугольного треугольника
Чему равна сумма острых углов прямоугольного треугольника? Это свойство прямоугольного треугольника вытекает из теоремы о сумме углов треугольника.
Утверждение.
Сумма острых углов прямоугольного треугольника равна 90º.
Дано:
∆ABC,
∠C=90º.
Доказать:
∠A+∠B=90º.
Доказательство:
По теореме о сумме углов треугольника,
∠A+∠B+∠C=180º.
По условию, ∠C=90º.
Отсюда, ∠A+∠B+90º=180º.
Следовательно, ∠A+∠B=180º-90º= 90º.
Что и требовалось доказать.